Мнимые парадоксы СТО. Парадокс Белла

Мнимые парадоксы СТО. Парадокс Белла

Путенихин П.В.
m55@mail.ru

На Википедии описание парадокса Белла приводится в следующем виде.

«Парадокс Белла – один из известных релятивистских парадоксов специальной теории относительности, связанный с невозможностью определения понятия «абсолютно твёрдого тела» в пространстве-времени теории относительности. В наиболее известном варианте самого Белла парадокс возникает при рассмотрении мысленного эксперимента, включающего в себя два ускоряющихся в одном и том же направлении космических корабля и соединяющую их натянутую до предела струну (один корабль летит строго впереди другого, т. е. ускорение направлено вдоль струны). Если корабли начнут синхронно ускоряться, то в сопутствующей кораблям системе отсчёта расстояние между ними начнёт увеличиваться и струна разорвётся. С другой стороны, в системе отсчёта, в которой корабли сначала покоились, расстояние между ними не увеличивается, и поэтому струна разорваться не должна. Какая точка зрения правильная? Согласно теории относительности, первая — разрыв струны» [1].

Решение «парадокса», несомненно, верное, хотя формулировка его не совсем точная. С точки зрения системы отсчета покоя расстояние между ракетами не изменяется, но трос при этом испытывает Лоренцево сокращение. Следовательно, он стремится либо притянуть ракеты друг к другу, либо растянуться вплоть до разрыва. С точки зрения сопутствующей системе отсчета, например, первой ракеты, трос, прикреплённый к ней, не растягивается, ведь это одна и та же система отсчета. Но вторая ракета отстаёт, поскольку между ней и первой, ведущей ракетой расстояние обязано увеличиться. Действительно, если для внешнего наблюдателя «длина интервала между ракетами» неизменно, то в собственных системах отсчета оно увеличивается. То есть, с точки зрения специальной относительности нет никаких противоречий.  Трос с очевидностью рано или поздно разорвётся, если он не обладает бесконечной растяжимостью.

Здесь мы исходим из определения логического парадокса как противоречия, которое имеет логически корректный вывод, приводящий к суждениям, взаимно исключающим друг друга. В этом смысле парадокс Белла как таковой, в сущности, не является парадоксом, поскольку его логически корректная формулировка не имеет взаимно исключающих выводов. Это рядовая, элементарная задача СТО и называть её парадоксом – явное преувеличение. Чтобы это увидеть достаточно даже вполне поверхностного знакомства с формализмом специальной теории относительности.

Трудно объяснить, например, как можно предполагать, что с точки зрения системы отсчета какой-либо из ракет расстояние между ракетами может быть неизменным? Если расстояние между ними неизменно в неподвижной системе отсчета, то это прямо означает, что собственная длина дистанции между ними с точек зрения любой из ракет (и с точки зрения троса) должна постоянно увеличиваться в соответствии с преобразованиями Лоренца. Только в этом случае дистанции между ракетами с точки зрения неподвижной системы отсчета будет неизменной.

Наоборот, также невозможно объяснить предположения, что с точки зрения исходной системы отсчета трос не сокращается. Это сокращение прямо следует из преобразований Лоренца.

Как видим, решение «парадокса» является очевидным, не требуется даже никаких вычислений. Трос сокращается, а крепления его концов - нет. Тем не менее, некоторых авторов «очевидность» решения, мягко говоря, не убеждает. Видимо, поэтому в литературе появляются различной сложности математические и не очень решения «парадокса». И даже такие, в которых трос остается целым. Авторы таких решений просто заблудились в собственных уравнениях. Не мудрено. Специально для решения этой задачи Белла формулируются собственные теоремы, выводятся уравнения, строятся диаграммы. Ситуация всё больше напоминает знаменитую схоластическую задачу «Сколько ангелов поместится на кончике иглы?»

Но к чему элементарную задачку возвеличивать до уровня парадокса? В подтверждение очевидности решения задачи Белла приведём весьма наглядную иллюстрацию этого: анимацию. Читателю даже не потребуется напрягать воображение.

Для большей наглядности заменим трос твёрдым нерастяжимым стержнем, который одним концом закреплен на первой, ведущей ракете, а вторым концом – легко разрушающимся соединением на второй, задней ракетой. В процессе движения задний конец стержня либо останется прикрепленным к ракете, либо выпадет из соединения. Этот разрыв соединения полностью соответствует попытке растянуть стержень - трос. Но для чего это нужно? В отличие от троса, собственная длина стержня всегда одна и та же, что позволит легко увидеть со стороны изменение его длины вследствие релятивистских эффектов. Заметить плавное растяжение троса несколько сложнее.

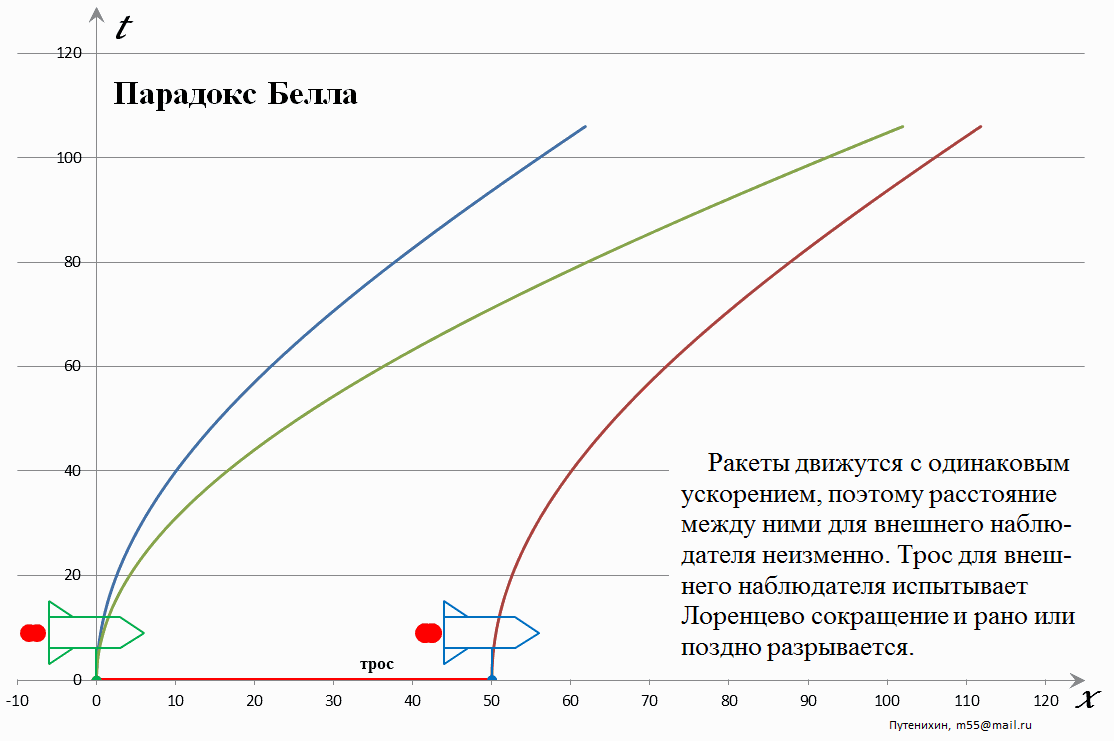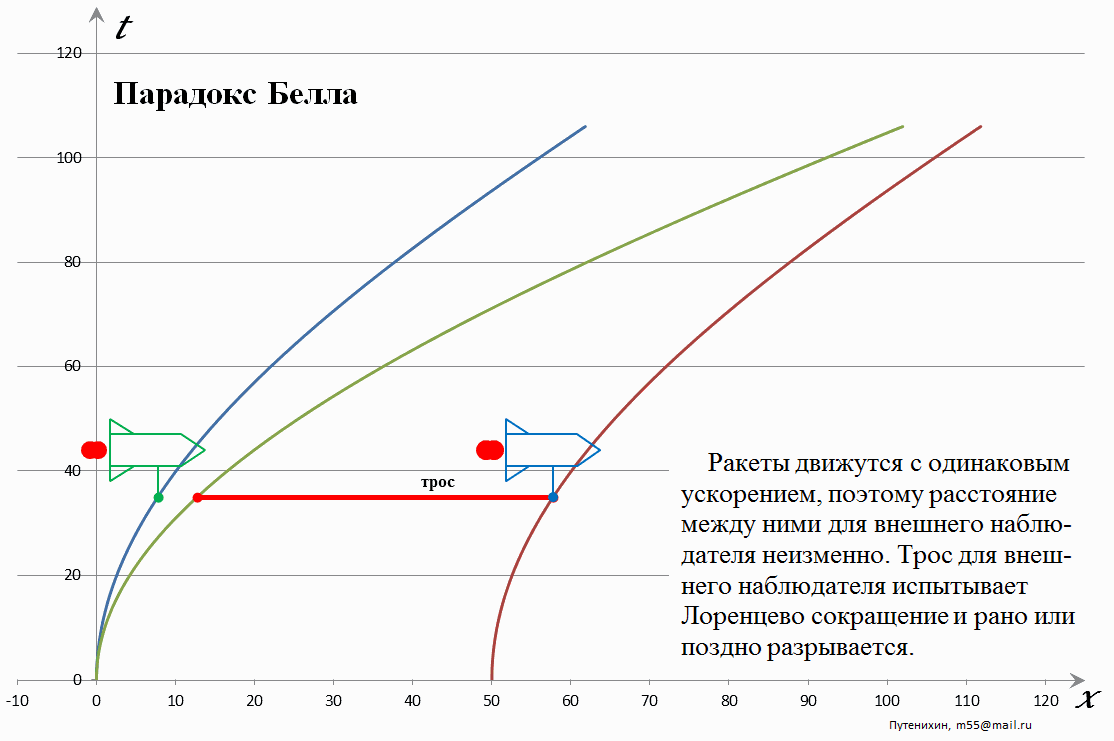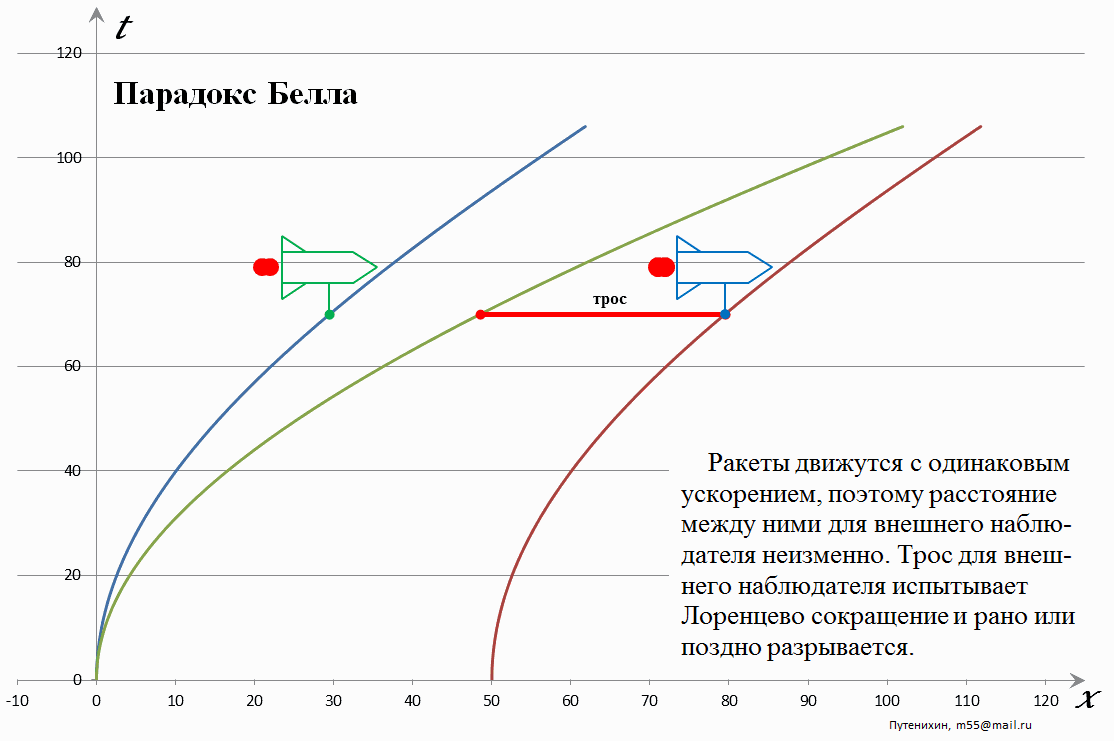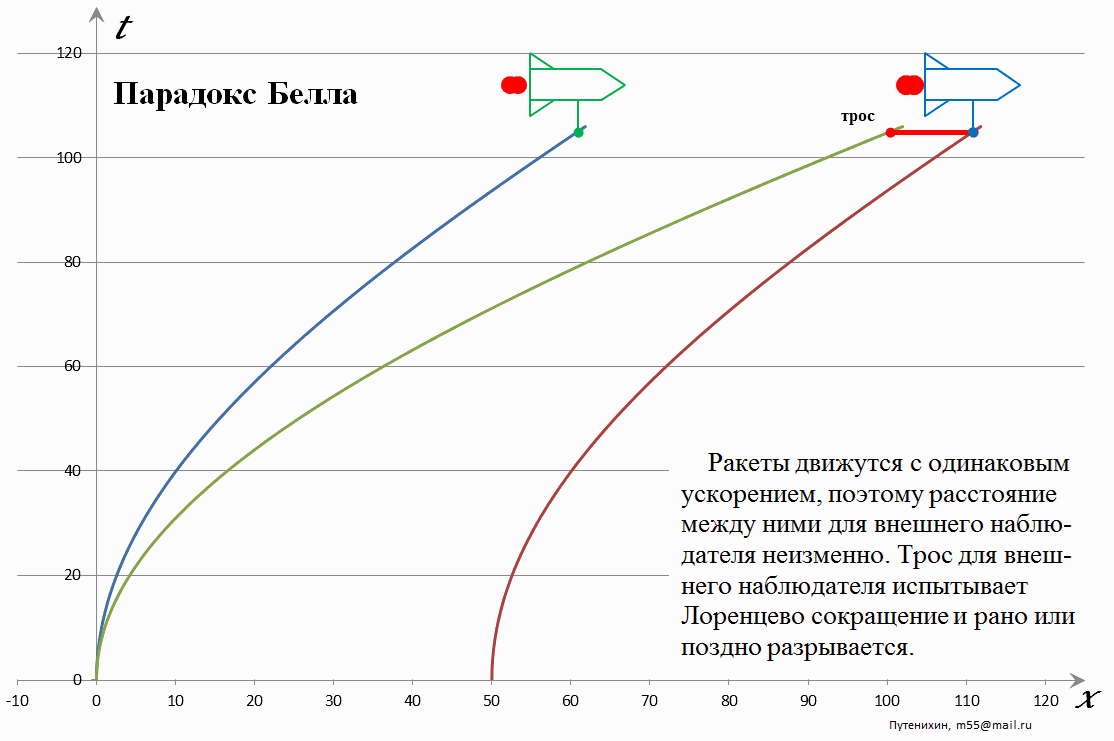
Рис.1 Лоренцево сокращение стержня при его ускоренном движении. Расстояние между креплениями, согласно условиям задачи, неизменно.

На рисунке (анимации) показана неподвижная (лабораторная, земная) система отсчета. Параболические линии – это мировые линии ракет и концов стержня (троса) в этой системе. У каждой ракеты вниз вынесены штанги с креплением, к которым привязаны нулевые координаты их собственных систем отсчета. Системы отсчета троса привязываются к его концам.

В начальный момент времени левая, ведомая ракета и левый конец стержня находятся в начале координат неподвижной системы отсчета. С её точки зрения в процессе ускоренного движения стержень начинает непрерывно сокращаться, хотя в его собственной системе отсчета с ним ничего не происходит. Согласно условиям задачи расстояние между ракетами неизменно. При этом мировая линия второй ракеты не совпадает с мировой линией «хвоста» стержня-троса. Это очевидно, поскольку вследствие постоянного сокращения стержня его конец движется быстрее, чем его начало. Конец стержня пытается «догнать» его начало. Скорости начала стержня и двух ракет равны, поэтому конец стержня «убегает» от второй ракеты, разрушая соединение с ней. Если же трос эластичен и может растягиваться, то разрушения на первых порах не будет. Для этого мы и заменили эластичный трос жестким, нерастяжимым стержнем, чтобы увидеть удлинение на самом начальном этапе. Для эластичного троса разрушающее растяжение и его разрыв может наступить намного позже, а само растяжение не сразу и видно. Отметим кстати, что с рассматриваемой точки зрения конец стержня и его начало находятся в разных системах отсчета! Это довольно любопытная ситуация: одному и тому же жесткому объекту не может быть назначена единая система отсчета. Отсюда также следует вывод, что стержню не может быть назначена и единая мгновенно-сопутствующая инерциальная система отсчета – МСИСО.

Итак, с точки зрения неподвижной системы отсчета отрыв стержня и разрыв троса очевидны.

Теперь перейдём в систему отсчета стержня. Здесь уже очевидно, что стержень и ведущая ракета образуют единую собственную систему отсчета. Они оба жесткие, скреплены друг с другом и движутся с одинаковой скоростью. Поэтому мировые линии ведущей, первой ракеты и концов стержня – прямые вертикальные линии.

Как было отмечено выше, с точки зрения неподвижной системы отсчета к стержню не может быть привязана единая мгновенно-сопутствующая инерциальная система отсчета - МСИСО. Но с точки зрения самого стержня и ведущей ракеты, к которой он прикреплен, этому нет никаких препятствий, ведь с их точки зрения они движутся с одной и той же скоростью.

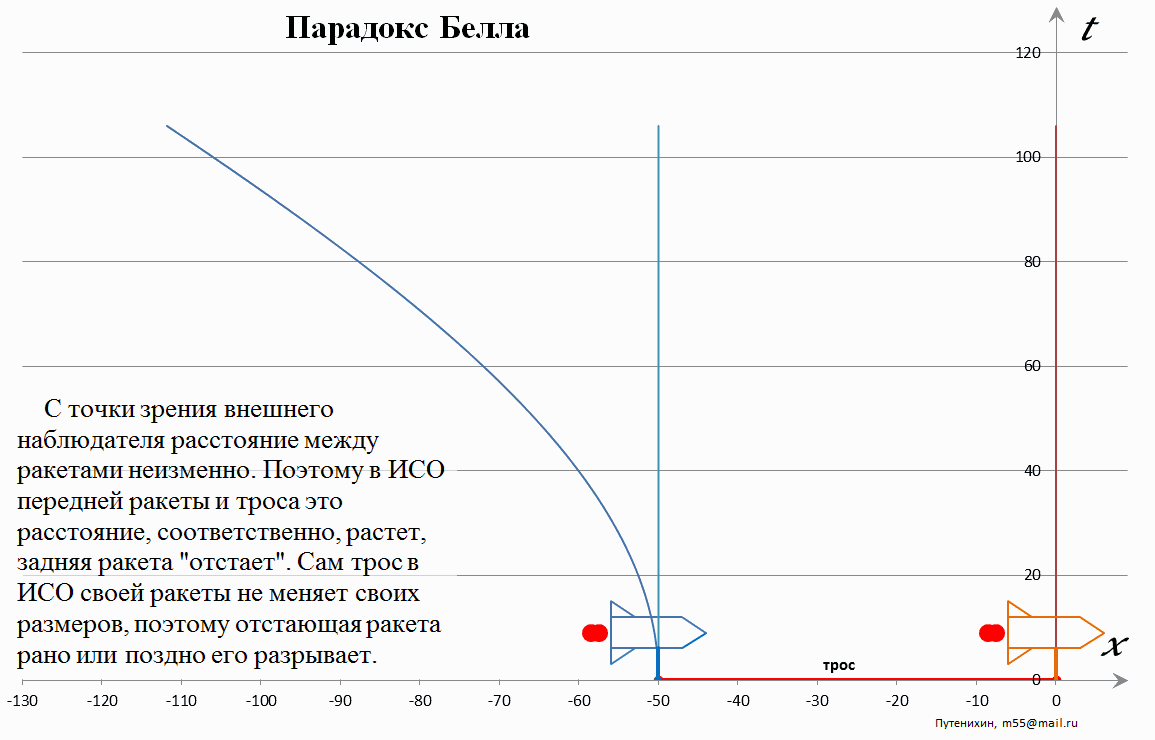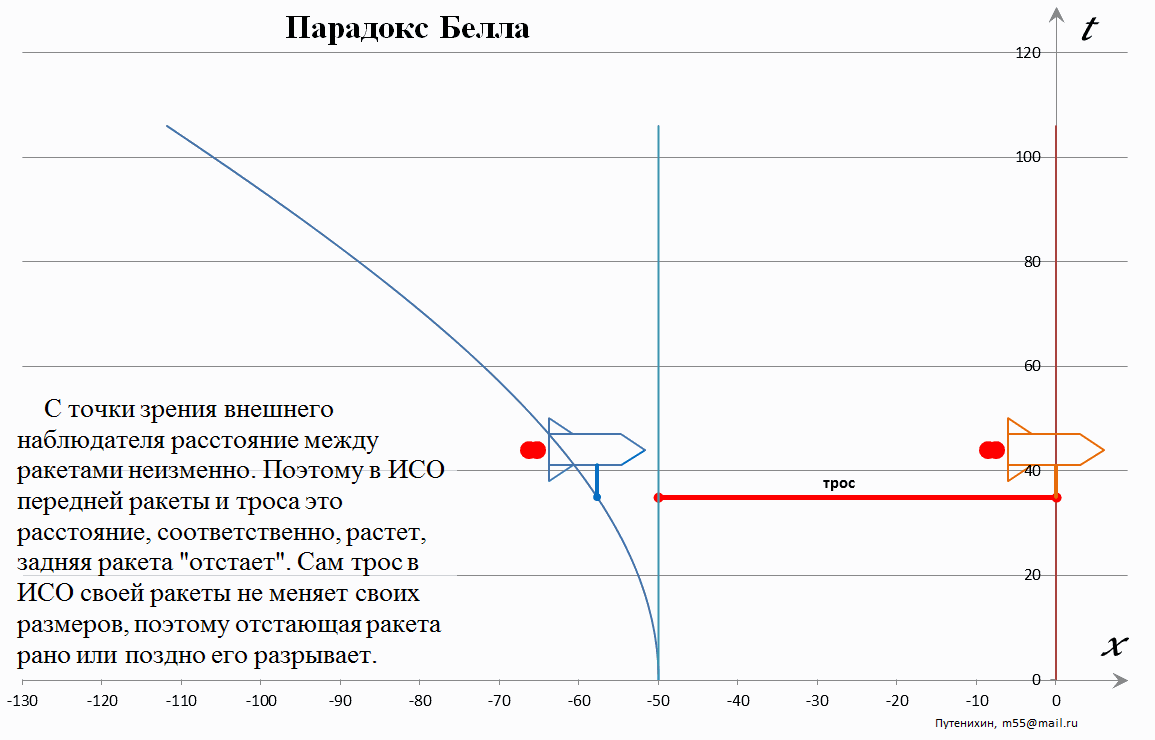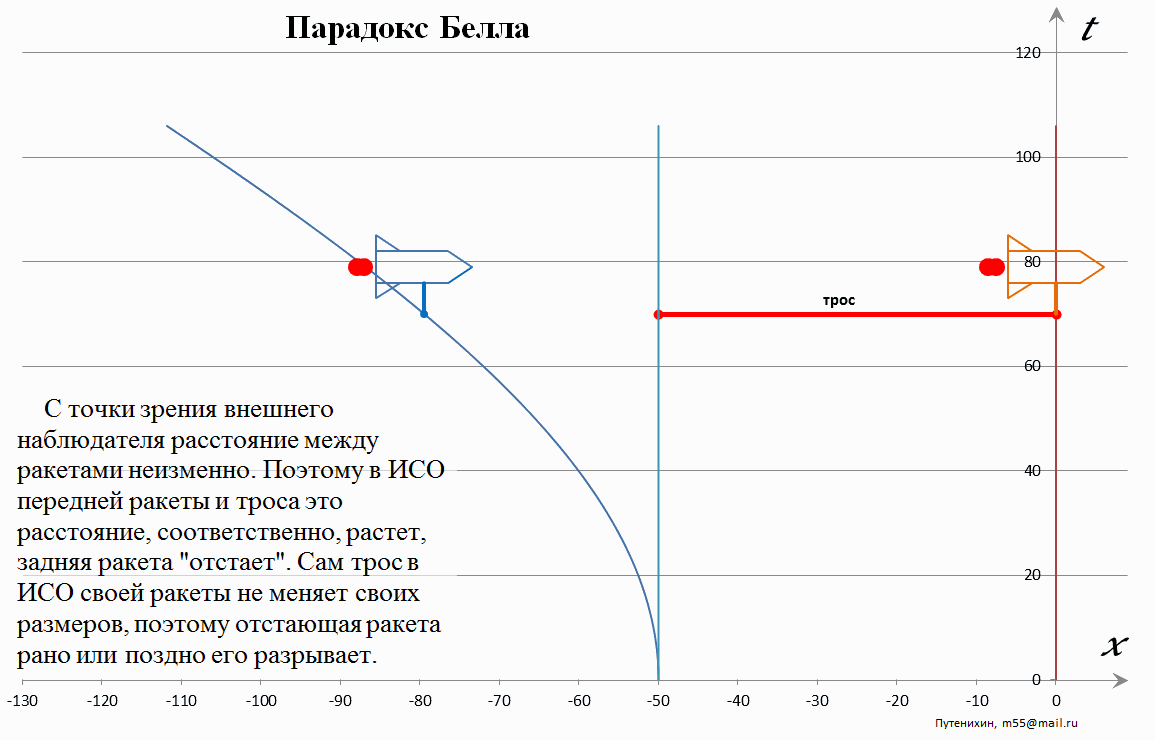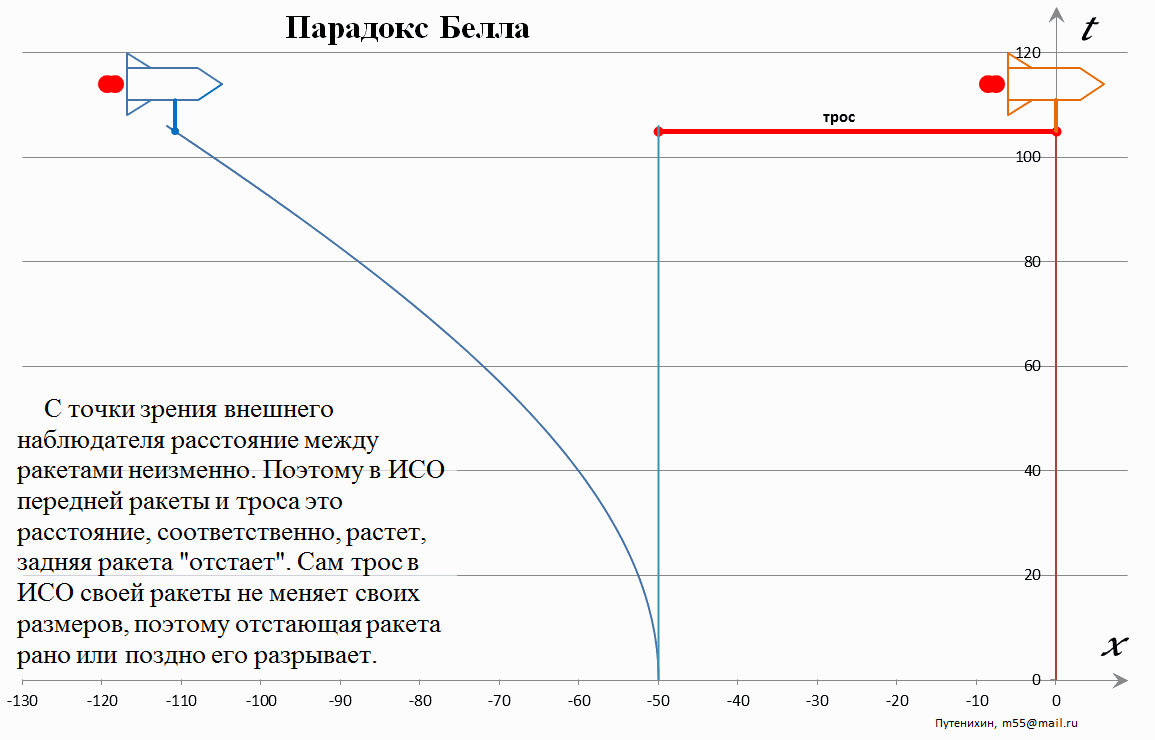
Рис.2 Лоренцево увеличения дистанции между ракетами. Длина стержня неизменна, поэтому расстояние между его концом и второй ракетой увеличивается.

Очевидно, что никакого парадокса не возникает также и с этой точки зрения – системы отсчета ведущей ракеты и стержня. Мировая линия второй ракеты в этом случае имеет параболическую форму, направленную от первой ракеты. Это не означает, что вторая ракет «летит хвостом вперёд», просто она отстает от первой ракеты. Согласно условиям задачи расстояние между ракетами в неподвижной системе отсчета неизменно. То есть для любой скорости движения ракет расстояние между ними одно и то же. Но согласно преобразованиям Лоренца это расстояние соответствует «укороченному» собственному расстоянию между ракетами в их системах отсчета. Другими словами, для каждого момента движения ракет, для каждого конкретного значения их скорости мы можем привязать к ним соответствующие МСИСО. При этом обе эти МСИСО будут иметь всегда одну и ту же скорость по отношению к неподвижной системе отсчета. То есть, обе ракеты будут фактически находится в одной и той же МСИСО. Из этого прямо следует, что дистанция между ними в этих МСИСО будет прямо зависеть от её скорости. Чем выше скорость, тем эта дистанция должна быть больше, поскольку только в этом случае «сокращённая» дистанция, согласно «обращенным» преобразованиям Лоренца, будет неизменной с точки зрения неподвижной системы отчета. Обращенные преобразования Лоренца – это преобразования, в которых по известной сокращенной длине стержня или дистанции между ракетами вычисляются их собственные длины.

Таким образом, в системе отсчета первой ракеты и стержня вторая ракета постоянно удаляется, что приводит к разрыву крепления со стержнем. Ну, или соответствующему растяжению и последующему разрыву троса.

В заключение отметим, что на анимациях для релятивистской корректности вычислений – невозможности превысить скорость света – величина ускорения взята «релятивистской»:

При движении ракет от состояния покоя до скорости, близкой к скорости света, фактическое ускорение будет стремиться от исходного значения а₀ к нулю. В этом случае скорость ракет также будет ограничена скоростью света: на приведённых анимациях она достигает величин порядка 0,98с. Также для простоты вычислений на анимациях началу и концу стержня всегда привязывается единая МСИСО.

Литература

1. Парадокс Белла, Википедия, URL: (https://ru.wikipedia.org/wiki/Парадокс_Белла).

2. Путенихин П.В. Мнимые парадоксы СТО. Теорема Белла, [рассмотрен парадокс Белла, в котором две ракеты, соединенные тросом, движутся с одинаковым ускорением. Трос со временем разрывается], URL:   
http://samlib.ru/p/putenihin_p_w/paradox-bell.shtml