Динамические диаграммы Минковского на примере обмена световыми сигналами

Динамические диаграммы Минковского на примере обмена световыми сигналами
Minkowski’s dynamic diagrams in the example of the exchange of light signals  

Putenikhin P.V.
m55@mail.ru

В докладе «Пространство и время» в 1908 году Герман Минковский предложил способ наглядного изображения физической реальности в виде четырехмерного пространства событий, в котором каждая точка представляет собой некоторое событие, определяемое тремя пространственными и одной временной координатами (Минковский Г. Пространство и время /в кн.: Принцип относительности. – М.: Атомиздат, 1973). Эти точки четырехмерного пространства-времени Минковского являются математическими абстракциями, которые не обладают ни пространственным объемом ни временной длительностью. В дальнейшем эти изображения получили название «диаграммы Минковского» и считаются наглядным способом демонстрации сущности специальной относительности и используются для доказательства её истинности.

Воспользуемся такой диаграммой и рассмотрим мысленный эксперимент с обменом световыми сигналами между двумя движущимися ИСО – А и В с относительной скоростью 0,866с. Традиционно далее мы будем использовать систему единиц, в которой скорость света с=1. В этом случае относительная скорость ИСО будет записываться как 0,866. Это значение мы задаём произвольно. Процесс будем рассматривать на диаграмме Минковского с точки зрения средней ИСО – С. Средняя ИСО – это система отсчёта, имеющая среднюю скорость, при которой каждая из двух подвижных систем удаляется от неё в противоположные стороны с одинаковыми скоростями, равными в нашем случае 0,577. Движение началось из общей точки, но мы будем рассматривать его через 120 секунд от начала, когда все участники удалились друг от друга на некоторое расстояние. Этот начальный момент эксперимента изображён на диаграмме:

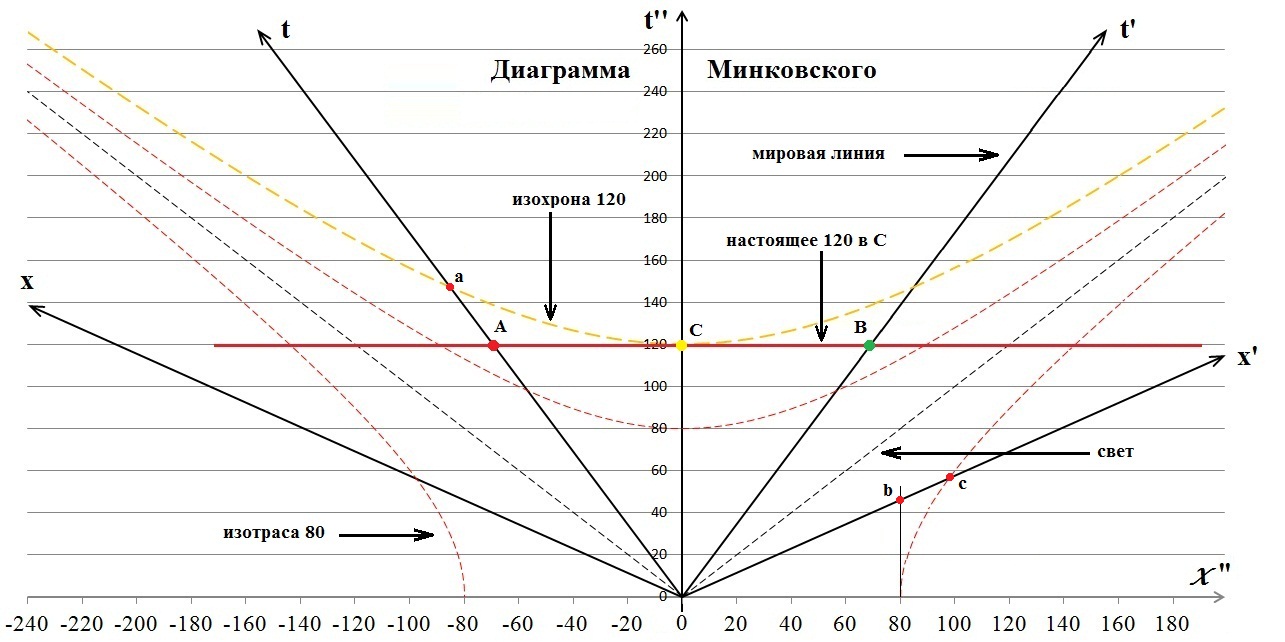
Рис.1 Диаграмма Минковского для двух движущихся систем отсчета А и В с точки зрения средней, неподвижной системы С в момент времени 120 секунд от начала движения.

Этот момент времени изображен на диаграмме оранжевой линией «настоящего времени в неподвижной системе отсчета (покоя)» или кратко «настоящее покоя». Тонкие штриховые линии, исходящие из начала координат и имеющие угол наклона к оси времени, равный 45^о, ‑ это мировые линии света. Все мировые линии движущихся систем отсчета имеют иметь угол наклона к оси времени только меньше 45^о.

Также на диаграммы для удобства последующих рассуждений добавлены традиционные вспомогательные линии (калибровочные кривые, «семейство гипербол»). В литературе у них нет общепризнанного названия, поэтому для определенности назовём их изохронами. Такое название вполне допустимо, оно точно отражает смысл этих линий. Изохрона отсекает на всех без исключения мировых линиях ИСО, движущихся из начала координат, отрезки равного времени, прошедшего от начала движения. Понятно, что изохрон на диаграмме Минковского может быть бесчисленное множество - по величине времени, отсекаемого на мировых линиях ИСО, все они в нашем случае описываются уравнениями гипербол t²=x²+t_i². Изохрона 120, изображенная на приведённой диаграмме желтой штриховой линией, показывает, что во всех ИСО, мировые линии которых дошли до неё, прошло ровно t_i=120 секунд от начала движения по их собственным часам.

Все изохроны на диаграммах Минковского располагаются «вдоль» вертикальной оси ветвями вверх (движение в будущее) или вниз (движение из прошлого). Мы будем рассматривать только верхнюю часть диаграмм, для времени от нуля и выше. К изохронам «ортогонально» располагаются соответствующие гиперболы, которые можно назвать «изотрасами» (или изотрассами) - ветвями вправо (удаление от неподвижной ИСО вправо) или влево (удаление от ИСО влево). Это линии, отсекающие на мировых линиях расстояний отрезки равных дистанций (трасс), то есть, показывающие одинаковое расстояние от начала координат во всех движущихся ИСО. Уравнения изотрас – x²=t²+x_i². На рисунке красными линиями показан «комплект» изохроны 80 и соотвествующей ей изотрасы 80.

Изохроны и изотрасы на бесконечности сколь угодно близко приближаются к мировым линиям света, но никогда не коснутся их. С помощью изохрон и изотрас на диаграмме можно наглядно продемонстрировать некоторые кинематические эффекты преобразований Лоренца. Например, точка a обозначает на диаграмме момент времени ИСО А, когда её часы будут показывать время 120 секунд, поскольку эта точка лежит на соответствующей изохроне. Но в «настоящем» системы С часы системы А показывают другое время, ведь они идут с её точки зрения замедленно. Это замедление можно определить по диаграмме (с учетом пропорций, поскольку диаграмма на рисунке слегка вытянута по горизонтали). Замедление равно:

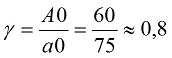
Поскольку скорость системы А равна 0,577, то этот же коэффициент, вычисленный по уравнениям Лоренца, равен:

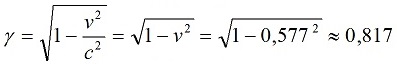
Соответственно, с точки зрения неподвижной системы С система В удалилась от начала координат за 80 секунд движения на расстояние 80 световых секунд. Но с точки зрения системы В она прошла путь, который также короче за счёт лоренцева сокращения отрезков. Это сокращение по измерениям на рисунке равно той же величине:

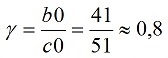
Ещё нагляднее на диаграмме демонстрируется знаменитая «относительность одновременности». Два события – b и c – в системе отсчета В находятся на линии одновременности – оси x’. Все события, находящиеся на линии, параллельной оси расстояний – одновременные, они произошли в один и тот же момент времени. Но с точки зрения неподвижной системы С эти два события имеют разное время свершения. Событие b, например, произошло приблизительной в 45 секунды. Событие с – приблизительно в 57 секунд.

В данной работы мы будем использовать на всех последующих диаграммах изменяющийся масштаб, то есть, значения возле меток на осях координат будут постоянно возрастать вместе с течением времени. В этом случае линия настоящего и начало координат будут неподвижны. Напротив, если использовать фиксированный масштаб, то в рассматриваемом нами эксперименте квадрат 80х80 пространственно-временных координат в начале движения, преобразуется в конце движения в квадрат 1000х1000, то есть исходную диаграмму к этому моменту необходимо увеличить в 12,5 раз. Динамическое масштабирование даёт один и тот же размер диаграммы в обоих случаях, изменяется только цена делений осей.

Другим следствием такого масштабирования будет то, что движущиеся во времени события и неподвижная (лабораторная) ИСО с линией «настоящее покоя» окажутся «замороженными» в своих определенных, начальных точках диаграммы. Наоборот, события, имеющие определённое, фиксированное время свершения, на диаграмме будут двигаться по своим мировым линии к началу координат (то есть, как бы в обратном направлении), оставаясь при этом в фиксированной точке пространства-времени. Такая диаграмма будет напоминать картину удаляющегося ландшафта: так выглядят деревья, дома, люди, если смотреть на них через заднее стекло уезжающего автомобиля. Все пропорции сохраняются, уменьшаются только размеры.

Итак, посмотрим на динамическую диаграмму Минковского для описанного случая:

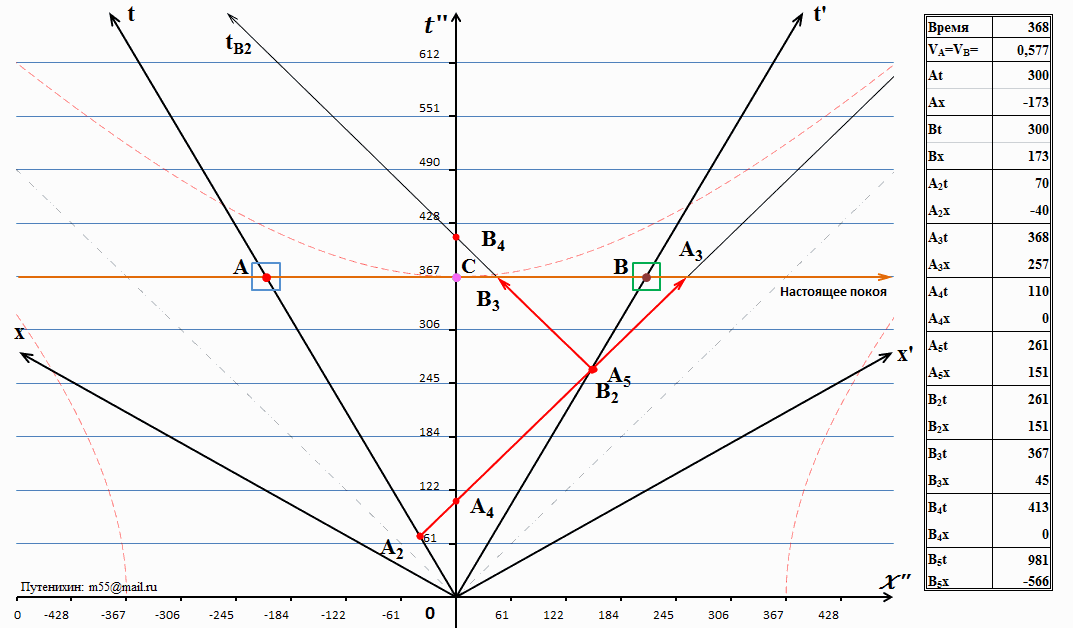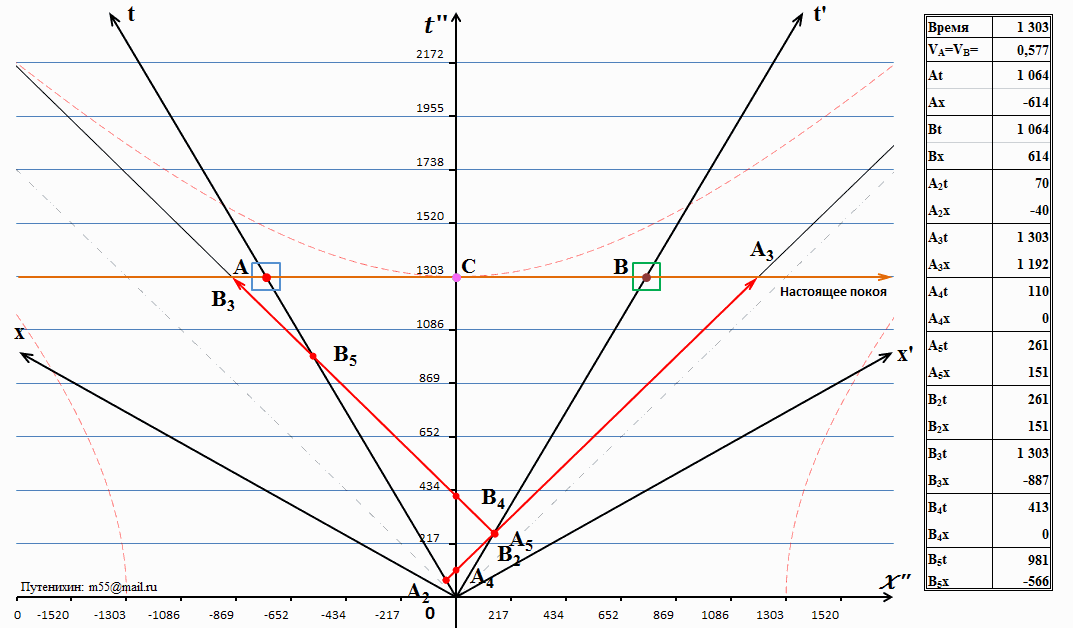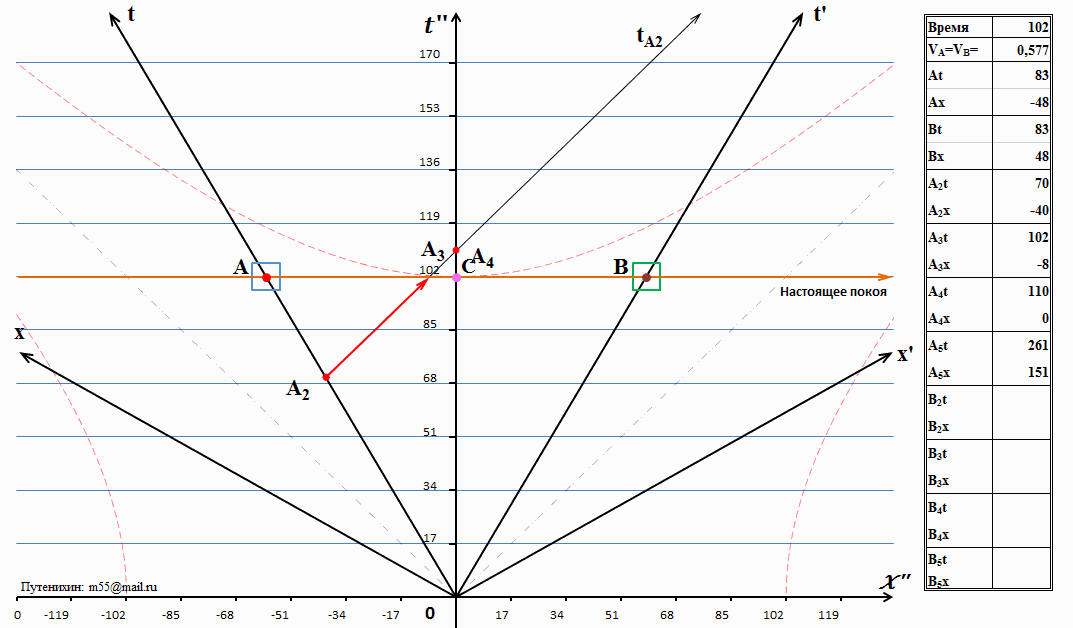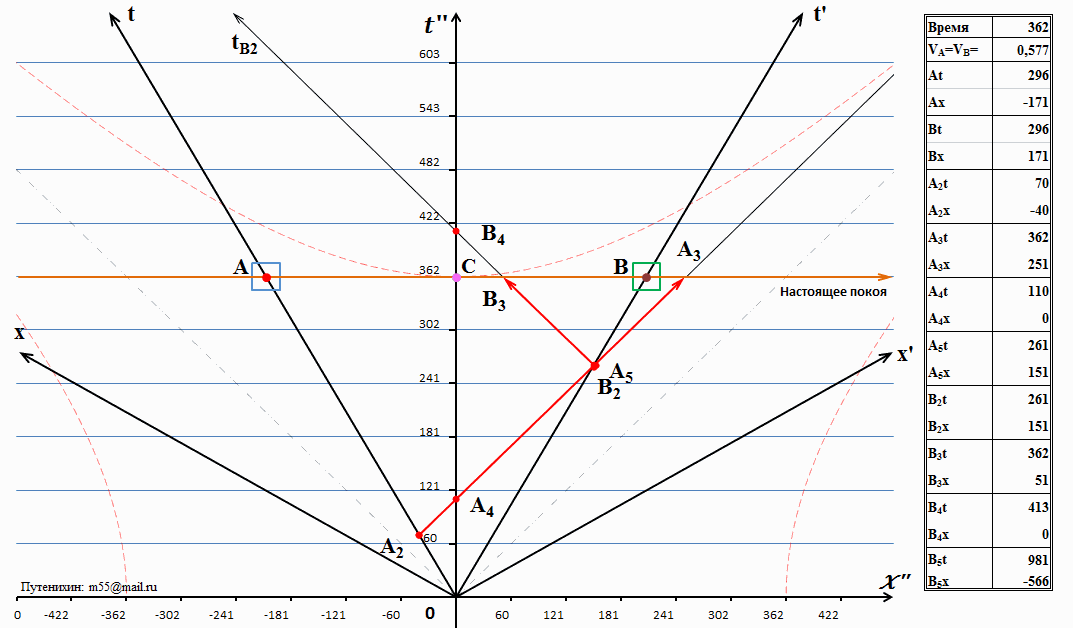
Рис.2 Динамическая диаграмма Минковского для эксперимента с обменом световыми сигналами между двумя системами отсчета А и В с точки зрения неподвижной системы С (анимированный gif-файл).

Рассмотрим подробно, насколько удастся, все происходящие на диаграмме события. Как сказано выше, рассматривать картину будем с момента времени 65 секунд, прошедшего от начала движения. В соответствии с СТО, часы движущихся систем А и В с точки зрения неподвижной системы С показывают время 65γ, где γ – лоренцев коэффициент, в нашем случае, как выше показано, равный 0,817.

То есть, с точки зрения неподвижной системы отсчета, часы А и В показывают 68х0,817=56 секунд, это точка пересечения мировых линий систем А и В с линией «настоящего» системы покоя. В точках, где изображены эти системы, на изохроне их собственные часы будут показывать 68 секунд.

Движение продолжилось, и в момент времени 57 секунд от начала движения по собственным часам система отсчета А посылает системе В световой сигнал:

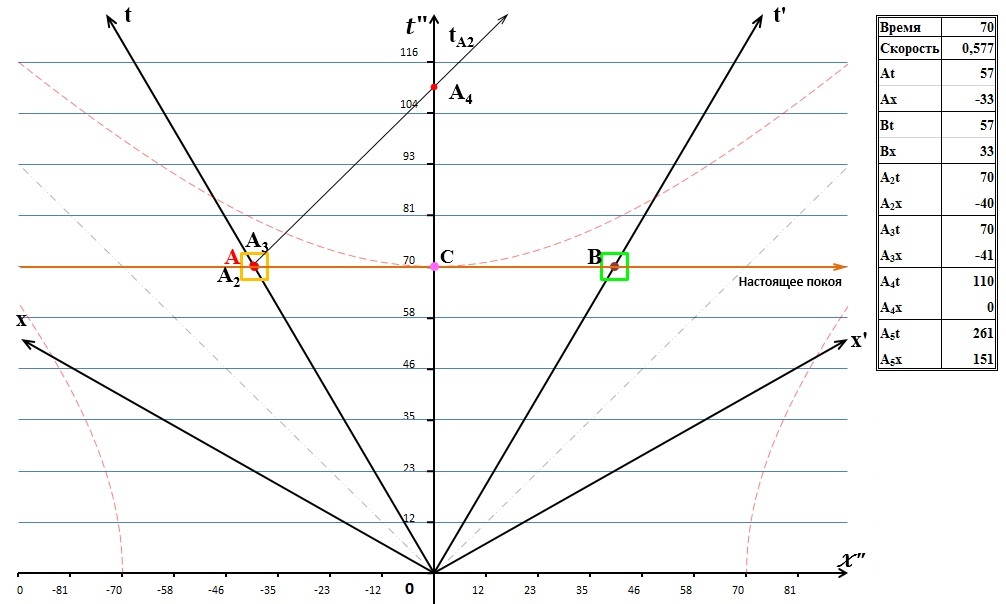
Рис.3 Система А излучает световой сигнал в сторону системы В

По часам неподвижной системы С это событие произойдёт в 70 секунд от начала движения. Мировая линия светового сигнала t_A2 имеет наклон к оси времени 45 градусов, такой же, как и мировые линии света, и направлена вправо, в сторону системы отсчета В. Как видим на диаграмме, эта мировая линия пересекает другие линии диаграммы в определенных точках - событиях. Опишем их.

Событие А₁. Это событие на диаграмме показано без индекса. Это основное событие, именно оно образует мировую линию системы А.

Событие А₂ – это время свершения собственно события, которое назовём «испускание сигнала». На динамической диаграмме видно, что это событие в момент свершения геометрически совпадает с источником – системой А, что очевидно.

Событие А₃ опишем ниже.

Событие А₄. Видим, что это точка пересечения мировой линия сигнала t_A2 с мировой линией системы С. Пересечение мировых линий означает, что события двух систем отсчета находятся в одной и той же точке пространства-времени. В нашем случае это означает, что световой луч и система С встретились, это момент времени, когда свет прошёл через С. В таблице рядом с диаграммой мы можем прочитать это время: 110 секунд по часам неподвижной системы С. На самой динамической диаграмме можно заметить, что этот момент времени, это событие хотя и как бы «движется» вниз по оси времени, в действительности всегда равно 110 секундам «настоящего покоя». Поэтому событие А₄ можно назвать «сигнал достиг системы С».

Событие А₅. Это событие находится за пределами диаграммы и пока не видно. Это событие появится в поле диаграммы в момент времени после 150 секунд движения по часам неподвижной системы:

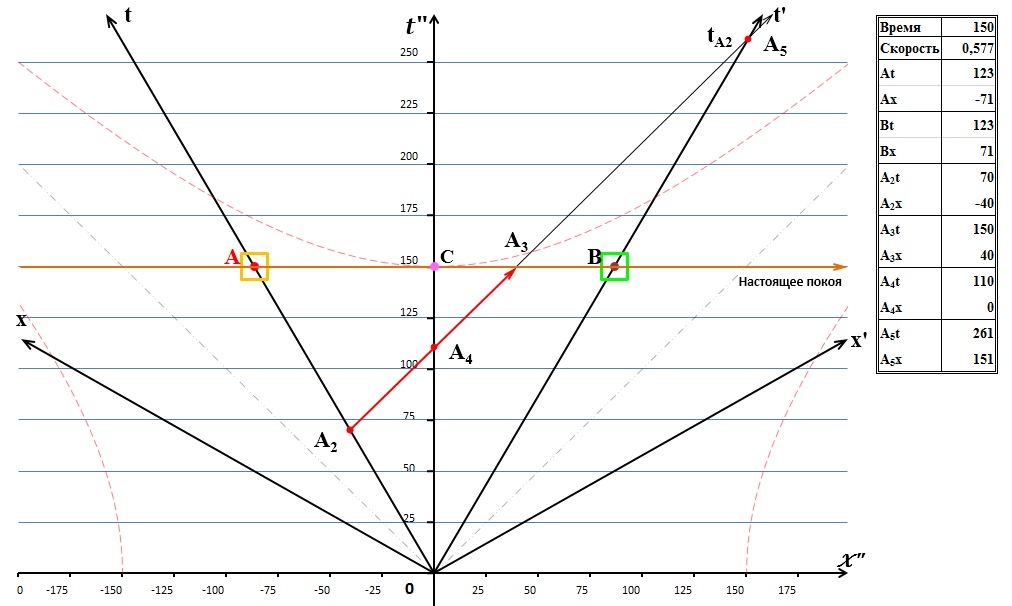
Рис.4 Мировая линия светового сигнала пересекла мировую линию системы В

Это событие соответствует пересечению мировых линий сигнала и движущейся системы В, следовательно, оно означает принятие сигнала этой системой, поэтому его можно назвать «сигнал от А прибыл в В». Очевидно, что время этого прибытия однозначно определено и в процессе движения, в нашем примере оно равно 261 секунде и не может меняться. Это мы и увидим в таблице параметров движения, показанной рядом с диаграммой. Там уже видно, что, как и следовало ожидать, на диаграмме не изменились время наступления события А₄ – 110 секунд и время испускания сигнала А₂ – 70 секунд. Событие А₃ переместилось на свободное поле диаграммы и теперь его можно описать.

Событие А₃. Очевидно, этому событию следует дать название «сигнал находится в настоящем неподвижной системы отсчета». Сигнал покинул систему А, затем прошёл мимо системы С и продолжил своё движение в пространстве. Очевидно, что этот сигнал не может быть «в прошлом» и не может быть в «будущем». Если сигнал будет поглощён, то у его мировой линии возникнет обрыв, она прервётся, и в этом месте будет зафиксировано новое событие «поглощение сигнала А₃».

Продолжим движение в пространстве-времени и посмотрим на следующий рисунок, на котором не происходит никаких новых событий. Это промежуточное состояние:

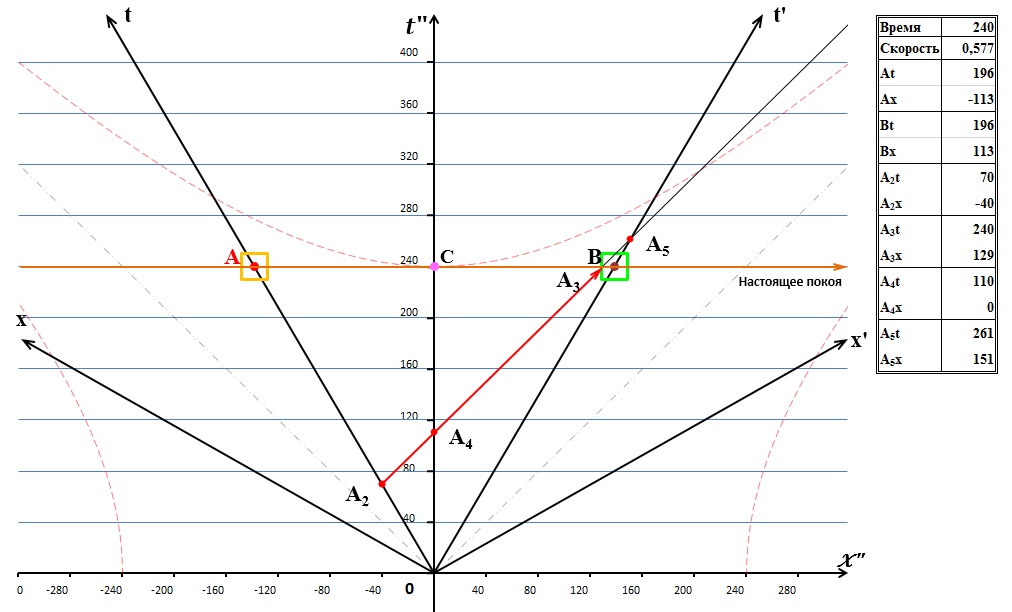
Рис.5 Световой сигнал вплотную приблизился к системе В

Здесь мы лишь отметим, что, как сказано выше, время наступления событий А2, А4 и А5 – это строго определённые времена, они фиксированы и не могут меняться в процессе движения. Это мы видим в таблице, которая в числовом виде показывает время наступления каждого из событий на диаграмме. Однако, хорошо заметно на диаграмме по таблице, что время события А₃ изменяется и неуклонно приближается к времени А₅. При этом время события В, то есть положение системы В в пространстве-времени диаграммы Минковского всегда находится между этими двумя событиями. Следует ожидать, что наступит время, когда совпадут события В, А₃ и А₅ по часам неподвижной системы. Действительно, такое совпадение происходит и возникает событие «сигнал А получен системой В». Одновременно с получением сигнала из А система В излучает ответный сигнал – В₂. Время этого события «излучение ответного сигнала» равно  262 секундам по часам неподвижной системы С:

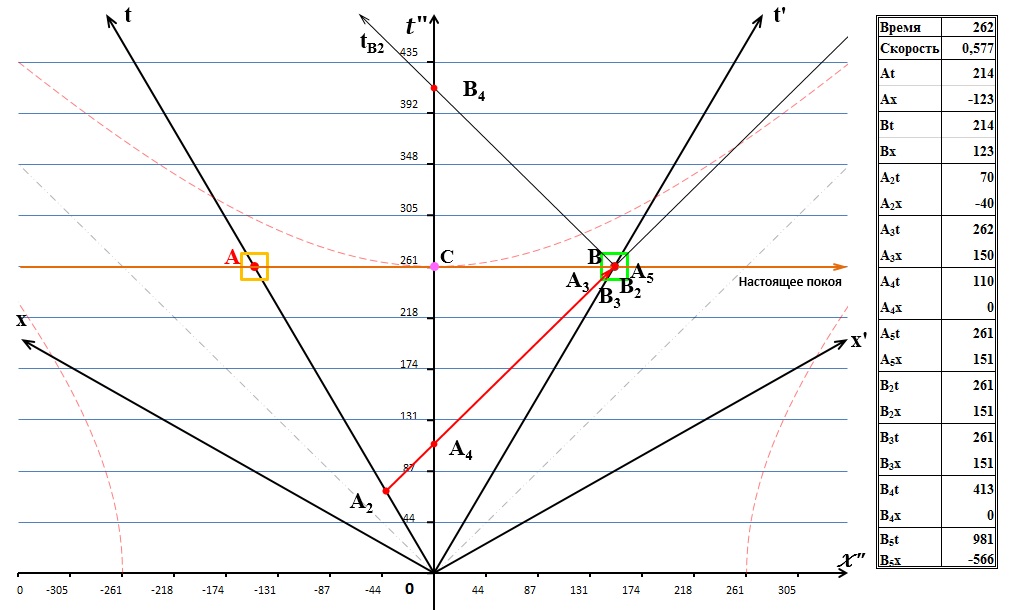
Рис.6 Система В излучает ответный световой сигнал в сторону системы А

Очевидно, что события В₁-В₅ имеют тот же смысл и схожие названия, что и события А₁-А₅. Также очевидно, что время наступления событий В₂, В₄ и В₅ будут неизменны на всей протяженности движения. Это мы увидим из таблицы к последующим рисункам. Как и ранее, событии В₅ оказалось за пределами диаграммы и также появится в её поле в дальнейшем. Но, даже не видя этого события, мы можем заметить, что наступит оно в 981 секунду и на расстоянии -566 световых секунд по часам неподвижной системы отсчета С. А пока посмотрим на ещё одну промежуточную диаграмму:

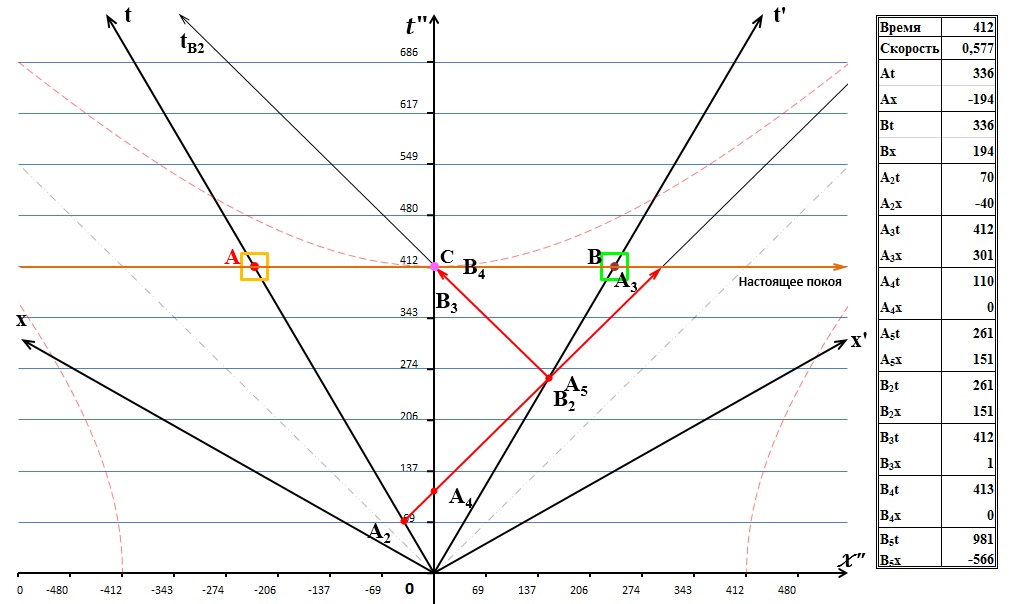
Рис.7 Сигнал системы В прибывает в систему С

Здесь можно обратить внимание на совпадение событий В₃, В₄ и С. Ясно, что это совпадение означает прибытие ответного сигнала В в систему С. Событие В₄, как и в предыдущем случае с сигналом А₃, так и называется - «прибытие ответного сигнала В в систему С». С этим событием пересеклись также линии «настоящее покоя» и «ответный сигнал находится в настоящем неподвижной системы отсчета», что означает прибытие ответного сигнала в С именно в настоящий момент времени.

Из таблицы и диаграммы мы видим неизменность времени совершения некоторых событий, а также одинаковое время и место событий А₅ и В₂. Это очевидно, ведь они произошли в одной точке пространства-времени, и это место не может быть изменено. Эти события неразлучной парой движутся в прошлое.

Рассмотрим ещё одну промежуточную диаграмму, время перед самым наступлением события поглощения ответного сигнала:

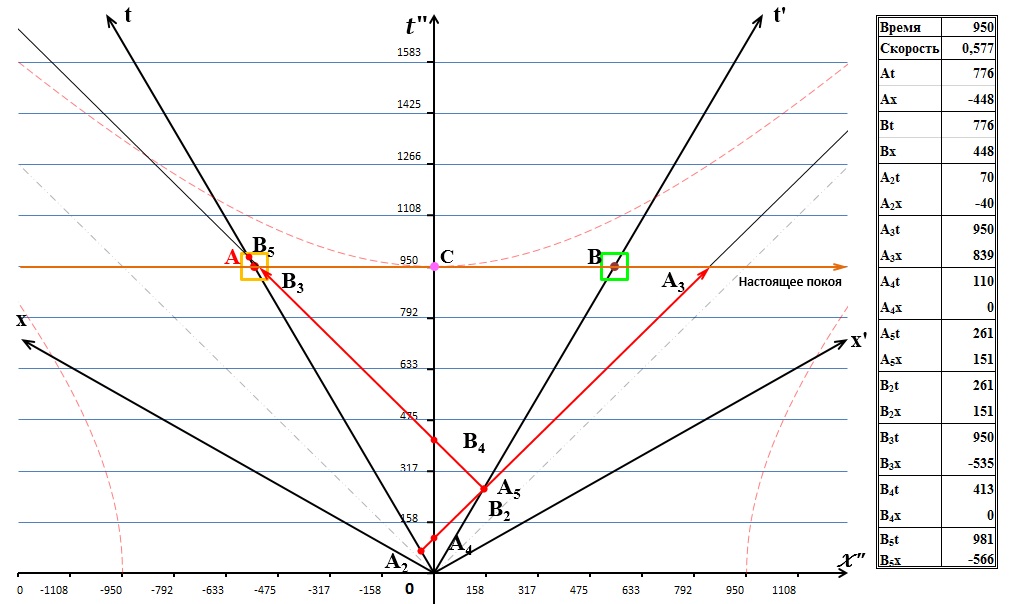
Рис.8 Сигнал системы В находится вблизи системы А

Никаких новых событий здесь не произошло. Мы лишь можем проверить, что время наступления некоторых событий, как и было заявлено, не изменилось. До наступления события «поглощение ответного сигнала В системой А» осталось всего 31 секунда. Эта диаграмма с поглощением ничем не будет отличаться от данной диаграммы, лишь совпадением в одной точке пространства-времени событий В₃, В₅ и А. Поскольку они и так достаточно близки друг к другу, мы эту диаграмму и не приводим. Вместо этого мы посмотрим на диаграмму в более далёком будущем. Как будет выглядеть картинам, например, через 100 000 секунд? Вот эта последняя в нашей статье диаграмма:

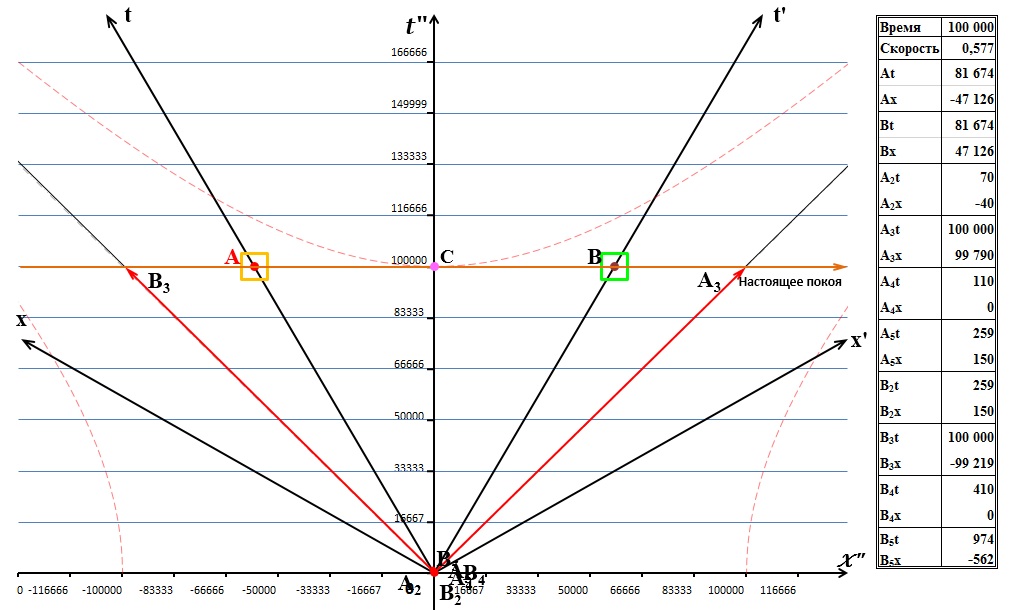
Рис.9 Состояние систем А, В и С через 100 000 секунд от начала движения

Все события, ушедшие в прошлое настолько близки друг к другу, что фактически слились в одну точку. Их обозначения, словно пчелиный рой, тоже наложились друг на друга так, что их сложно прочитать. На открытом поле диаграммы остались лишь события, действительно движущиеся в пространстве-времени – сигнал А3, ответный сигнал В3 и системы А, В, С. Вся наша экспериментальная «установка» растянулась в пространстве на 100 000 световых секунд в обе стороны.

Из таблицы видно, что с точки зрения систем В и С они удалились на расстояние ок.47 тысяч световых секунд и по их собственным часам прошло время ок.82 тысяч секунд. Это точно соответствует уравнениям Лоренца:

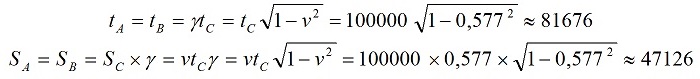
При изучении диаграмм у читателя может возникнуть резонный вопрос: почему все системы отсчета А, В и С изображены на одной горизонтали – линии «настоящего системы покоя»? Это их правильное изображение, хотя в литературе часто можно встретить их смещённое по вертикали расположение. Действительно, все события как на диаграмме Минковского, так и в реальности могут происходить только в настоящем времени. Ни одно событие не может происходить ни в будущем, ни в прошлом. События будущего – это, так сказать, предсказанные события, которые, разумеется, ещё не произошли и не происходят. Но время «настоящего», в котором они когда-то произойдут, нам уже известно. И только в это время, когда оно станет настоящим, совместится с линией «настоящее покоя» (на нашей диаграмме), только в это время эти события могут произойти. Но тогда это будет уже не будущее, а настоящее. Понятно, что у каждой системы отсчёта собственное «настоящее покоя», поэтому с их точки зрения рассмотренная диаграмма будет иметь совершенно иной вид.

Напротив, события прошлого уже свершились. То есть, они точно так же, как и события будущего, не происходят, не свершаются. Время их происхождения – это уже навсегда однозначно определённое, неизменное время. На нашей диаграмме такие события в самом наглядном виде «уходят в прошлое», двигаясь вниз по шкале времени, становясь достоянием истории.

Второй вероятный вопрос – почему стре́лки-события А₃ и В₃ словно скользят по линии настоящего? Это также должно быть понятно. Эти события являются фронтом световых сигналов, группой квантов, движущихся в пространстве-времени. Ни одно событие не «живет» в прошлом, ни одно событие не «живет» в будущем. Реально каждое событие имеет место только в настоящем. Настоящее постоянно движется по шкале времени, поэтому все «действующие» события движутся вместе с настоящим и могут «отстать» от него только в случае прекращения своего существования, завершения события. Такую картину можно сравнить с кинофильмом. Мы видим на экране неподвижную кабину и сидящего в ней водителя, а навстречу ему движется дорога. Точно так же и здесь: мы видим неподвижные системы отсчёта, а навстречу им движутся дорога «время» и дорога «расстояние». Стре́лки событий А₃ и В₃ движутся быстрее, поэтому они похожи на ещё два автомобиля, обгоняющие упомянутого водителя из кинофильма.