Модели памяти и внимания
ОСЦИЛЛЯТОРНЫЕ НЕЙРОННЫЕ СЕТИ. МАТЕМАТИЧЕСКИЕ РЕЗУЛЬТАТЫ И ПРИЛОЖЕНИЯ
6 Осцилляторные модели памяти и внимания
Среди различных нейросетевых моделей памяти наиболее известной и популярной является модель Дж. Хопфилда [51,52]. Она представляет собой однослойную нейронную сеть со связями "все на всех", в которой запоминаемым паттернам соответствуют стационарные состояния сети. Запоминание информации происходит путем формирования определенных коэффициентов связи между элементами сети. Важной особенностью памяти в сетях Хопфилда является ее ассоциативность: после того как сеть "запомнила" некоторый набор паттернов, она может воспроизвести любой из них даже в том случае, если этот паттерн подается на вход сети в искаженном виде.
В сети Хопфилда используются традиционные пороговые нейроны с симметричными связями, что гарантирует эволюцию сети к одному из ее стационарных состояний. Однако оказалось, что идеи Хопфилда имеют довольно общий характер и могут быть использованы при большей или меньшей модификации и в осцилляторных сетях. В этом случае запоминаемым образам по-прежнему соответствуют стационарные состояния, но уже не исходной ОНС, а некоторой новой динамической системы, получающейся из исходной с помощью подходящей замены переменных.
Проиллюстрируем сказанное конкретными примерами.
В работе Я.Б. Казановича и др. [60] предложена модель ассоциативной памяти в сети фазовых осцилляторов, в которой модификация текущих частот происходит в дискретные моменты времени. В результате функционирования сети все осцилляторы синхронизуются на некоторой частоте, но часть осцилляторов становится синфазной, а фазы других осцилляторов будут отличаться от них на л. Это позволяет установить соответствие между финальными состояниями сети Хопфилда и сети из фазовых осцилляторов, считая, что первая группа находится в состоянии "1", а вторая - в состоянии "0". Таким образом, информация в сети запоминается в виде фаз. Если правила обучения в сети Хопфилда и в данной сети фазовых осцилляторов одинаковы, то и запоминаемая этими сетями информация будет идентичной.
Аналогичный подход к моделированию памяти, но с использованием фазовых осцилляторов в непрерывном времени вида
![]()
где f - периодическая нечетная функция, предложен в работе А.Ю. Плахова и О.И. Фисуна [б]. Показано, что при определенных условиях запоминание информации в данной ОНС происходит более эффективно, чем в сети Хопфилда. Близкий подход к построению ассоциативной памяти, но с использованием в качестве элементов сети осцилляторов Ван-дер-Поля описан в работах Л. Абботта [10,11].
Другие варианты сети с ассоциативной памятью предложены в работе А. Ноеста [87]. Элемент сети носит название фазора, его состояние задается комплексным числом z = еi, модуль которого равен 1. Коэффициенты связи между фазорами также комплексные, что приводит к сдвигу аргумента передаваемого комплексного сигнала. Формально сеть не является осцилляторной, но возможность ее осцилляторной реализации достаточно очевидна.
Пусть сjk - коэффициент связи между фазорами j и k (сjk = сkj, сjj = 0); hj - сигнал, поступающий на j-й фазор:
![]()
Тогда динамика сети описывается системой уравнений
![]()
Функция Ляпунова для сети фазоров имеет вид
![]()
При запоминании паттернов (наборов аргументов 1,...,N) формирование коэффициентов связи осуществляется по правилу, которое является комплексным аналогом правила обучения в сети Хопфилда.
В работе Ф. Хоппенштедта [54] рассмотрена модель памяти в сети фазовых осцилляторов с локальными связями. Речь идет об алгоритме обучения сети из осцилляторов VCON (см. раздел 2), расположенных на окружности и связанных локальными возбуждающими или тормозными связями. Такие сети автор называет розетками. Обучение моделировалось путем увеличения силы связи между осцилляторами при синхронизации входа VCON и его ответа. Предположим, что все осцилляторы розетки работают синхронно с одинаковыми частотами 1. Затем на вход одного осциллятора подается возмущение, которое приводит к синхронизации системы, но уже с другим соотношением частот (см. определение синхронизации ОС 3 в разделе 2). Если включить обучение, то постепенно веса связей стабилизируют свои значения и в системе установится режим синхронизации на частоте 2. Обученная розетка без внешнего входа синхронизуется на частоте 1, но если подать внешний вход на любой из осцилляторов, то синхронизация установится уже на частоте 2. Тем самым система воспроизведет запомненную информацию. Отметим, что в данном случае рассматривалась лишь идея реализации памяти на ОНС, а проверка работоспособности сети проводилась на ЭВМ.
Задача запоминания информации в сети из нейронных осцилляторов сложнее, чем в случае сети из фазовых осцилляторов. В работе Д. Уанга и др. [118] предложен пример ее решения с использованием нейронных осцилляторов типа Вилсона-Коуэна (2.12) с задержкой в связях тормозных элементов "на себя". Обмен сигналами между осцилляторами идет через возбуждающие элементы. Активность элемента такой сети представляет собой чередование "пачек" высокочастотных колебаний (состояние "1") и интервалов отсутствия активности (состояние "0"). Переход от одного состояния к другому управляется входными сигналами на элементы сети. Коэффициенты связи между элементами формируются по правилу, сходному с правилом Хебба.
С помощью моделирования на ЭВМ в [118] продемонстрирована способность такой сети "запоминать" бинарные паттерны (конечные последовательности из нулей и единиц). Помимо этого сеть оказалась способной к сегментации сложного паттерна на составляющие. Сегментация выполняется следующим образом. Пусть сеть "запомнила" набор паттернов 1,2,...,k. Сформируем паттерн как смесь, например, трех паттернов 1,2, 3 так что начальная часть совпадает 1, средняя - с 2, а конечная - с 3. Добавим еще шум, изменив небольшое число компонент в . Тогда, как показывает один из примеров, приведенных в [118], при подаче на вход сети она некоторое время будет находиться в состоянии 1, затем перейдет в состояние 2, затем в состояние 3 затем снова в 1 и т.д. Время пребывания в каждом из этих состояний оказалось приблизительно равным продолжительности осцилляторной "пачки".
Важным параметром ассоциативной памяти является ее информационная емкость, т.е. количество паттернов, которые сеть способна запомнить и воспроизвести при заданном числе элементов. В смысле информационной емкости ОНС не дали пока каких-либо ощутимых преимуществ перед сетями Хопфилда. Но с точки зрения технических приложений они могут быть эффективны, если осцилляторная реализация элемента сети обладает какими-то преимуществами. Например, при оптической реализации нейронных сетей можно надеяться, что осцилляторные подходы окажутся плодотворными.
Переходя к рассмотрению моделей внимания, отметим, что в этой области еще не оформились общепринятые подходы и понятия. Поскольку многие нейрофизиологические данные свидетельствуют о том, что реализация функции внимания связана с синхронизацией электрической активности различных участков мозга, ОНС представляются наиболее перспективными для моделирования функции внимания.
Мы остановимся на трех известных нам подходах к моделированию внимания. Центральной идеей каждого из них является интерпретация внимания в терминах появления синхронизованной активности в определенных участках мозга. Согласно первому подходу внимание моделируется как способность к возбуждению и поддержанию высокого уровня колебательной активности в какой-то части сети в зависимости от подаваемого на вход набора сигналов. Согласно второму подходу, внимание трактуется как внутренняя способность кортикальных осцилляторов объединяться в синхронно работающие группы осцилляторов при отсутствии синхронизации между группами. Согласно третьему подходу, формирование группы синхронно функционирующих осцилляторов происходит с помощью центрального управляющего осциллятора, роль которого отводится септо-гиппокампальной области.
Первый подход представлен работами P.M. Борисюка и Ф. Хоппенштедта [22,55]. Работа [22] посвящена моделированию избирательности внимания. Для этого используется тот факт, что в фазовом пространстве отдельного нейронного осциллятора типа Вилсона-Коуэна (2.12) могут одновременно сосуществовать несколько аттракторов, например, состояние равновесия и предельный цикл. Предположим, что на распределенную по пространству сеть слабо взаимодействующих осцилляторов поступают одинаковые по амплитуде входные сигналы, но один из них представляет "особую важность". В начальный момент сеть получает указание о том, какой из одинаковых сигналов наиболее "важен", а далее поступающие сигналы неразличимы. Задача состоит в том, чтобы реакция сети на "важный" сигнал отличалась от реакции на все остальные сигналы. Чтобы реализовать такую "функцию внимания" предположим, что в начальный момент все осцилляторы находятся в состоянии равновесия и поступающие сигналы не выводят их из этого состояния. Но те осцилляторы, которые соответствуют "важному" сигналу, в результате дополнительного воздействия в начальный момент перейдут в колебательный режим и далее будут в нем оставаться. Аналогично может быть реализовано внимание и в том случае, когда поступающие на сеть сигналы со временем изменяют свое положение в пространстве.
В работе [55] модель внимания строится в сети из осцилляторов VCON. Это трехслойная сеть, слои которой интерпретируются как таламус, ретикулярная формация и неокортекс. Внимание в этой модели реализуется как возбуждение периодической активности в определенном элементе неокортекса в зависимости от наиболее сильного (значимого) сигнала из набора сигналов, поступающих на таламус.
Второй подход был развит в работе К. фон дер Мальсбурга и В. Шнайдера [81]. Предложенная в этой работе сеть состоит из 20 возбуждающих нейронов Е1, Е2, ... , Е20 со связями "все на всех" и одного тормозного нейрона I, получающего суммарный сигнал от всех нейронов Еi и тормозящего активность всех этих нейронов. Внешние сигналы и шум поступают на сеть через входы нейронов Еi. Взаимодействие нейронов Еi и I организовано таким образом, что при подаче на нейрон внешнего сигнала он генерирует пилообразные колебания. Нейроны Еi имеют рефрактерность, благодаря которой зубцы "пилы" отделены друг от друга периодами молчания нейрона.
В рамках данной модели синхронизация понимается в узком смысле как синфазность колебаний. Связи между возбуждающими нейронами Еi устроены так, чтобы синхронизовать активность этих нейронов. Роль тормозного нейрона I противоположная: если между колебаниями активности нейронов Еi и Еj есть ненулевая разность фаз, то под влиянием I эти нейроны будут стремиться работать в противофазе. Таким образом, синхронизация или десинхронизация зависит от конкурентного влияния взаимодействия возбуждающих нейронов между собой и воздействия на них тормозного нейрона.
Величины связей между нейронами Еi изменяются в ходе работы сети, и сформированные значения связей сохраняются в промежутках времени, когда входные сигналы на сеть не поступают. Правило изменения величины связи таково: связь увеличивается при синхронной работе нейронов и уменьшается, если колебания активности десинхронизованы. Такое правило обучения приводит к следующим достаточно очевидным последствиям.
Пусть на нейроны Е1, ..., Е10 в некоторый момент времени были одновременно поданы внешние сигналы (паттерн 1), а затем с некоторой задержкой были также одновременно поданы внешние сигналы на нейроны Е11, ..., Е20 (паттерн 2). Тогда после некоторого периода установления регулярной активности нейроны в каждой из групп 1-10 и 11-20 будут работать синхронно, а в разных группах колебания будут противофазными. Если сеть не обучена, одновременное предъявление двух паттернов приведет к установлению синхронных колебаний во всей сети. Если же обучение произошло и сильные внутригрупповые связи сформировались, то одновременная подача входных стимулов приводит под влиянием шума к образованию двух синхронно работающих групп осцилляторов, периоды активности которых находятся в противофазе друг к другу.
Третий подход к моделированию внимания сформулирован в работах В.И. Крюкова [72,73]. В его основе лежит принцип доминанты А.А. Ухтомского и ряд новых концепций обработки информации мозгом [2,26,83,116]. В отличие от распространенных моделей нейронных сетей, элементами которых являются отдельные нейроны, в данном случае элементом сети является ансамбль нейронов, функционирующий как осциллятор. Главной его особенностью является способность генерировать колебания, обладающие высокой стабильностью и периодом на порядок большим, чем характерное время срабатывания одиночного нейрона [З].
Сеть состоит из двух типов таких осцилляторов: кортикальных осцилляторов (КО) и септо-гиппокампального осциллятора (СГО), связанного со всеми КО, которые в свою очередь воздействуют на СГО через суммирующий элемент. В нейрофизиологических терминах КО интерпретируются как колонки неокортекса, а СГО как септо-гиппокампальная система, в которой источником осцилляции на частоте тета-ритма служит септум.
Как показано в работах [3,73] взаимодействие между осцилляторами в сети может быть приближенно описано системой фазовых уравнений
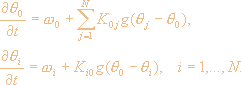
Здесь 0, i - фазы СГО и КО, 0, i - их собственные частоты, K0i, Ki0 - коэффициенты связи i-го КО с СГО и наоборот, g - функция, задающая взаимодействие осцилляторов. Таким образом, эти уравнения описывают сеть фазовых осцилляторов, в которой взаимодействие осуществляется через некоторый центральный осциллятор.
Появление синхронных колебаний СГО с какой-либо группой КО интерпретируется в модели как возникновение внимания. Изменяя собственную частоту СГО 0, можно выбирать группу КО, которые имеют собственные частоты близкие к 0 и будут синхронизоваться с СГО. Время на установление синхронизованных колебаний интерпретируется как время реакции или распознавания. Для его оценки могут быть использованы результаты, полученные в [З].
Архитектура рассматриваемой сети позволяет реализовать последовательную обработку поступающей информации от формирования фокуса внимания (FA) до записи в долговременную память (LTM). Промежуточным состоянием в этом процессе является формирование кратковременной памяти STM. В фокусе внимания находится та группа КО, которые в данный момент синхронизованы с СГО. Активизированные внешним воздействием КО, не входящие в FA, образуют STM. Переключение FA не приводит к немедленной десинхронизации уже сформированной группы синхронных осцилляторов. Эта группа какое-то время сохраняет синхронность без контроля со стороны СГО. Благодаря этому осуществляется превращение STM в LTM. Для этого используется принцип изолабильности, заключающийся в том, что осцилляторы, проработавшие достаточно большое время в синхронном режиме, постепенно меняют свою собственную частоту на ту, на которой они были синхронизованы. Эта частота сохраняется и после угашения колебаний и воспроизводится после того, как эти осцилляторы под внешним воздействием снова станут активными. Таким образом, запомненный в LTM паттерн активности может быть возвращен в STM или в FA.
Попадание осциллятора в FA может быть вызвано тремя причинами: появление нового стимула, замена имеющегося стимула на новый, спонтанная или целенаправленная активация с помощью СГО. Последнее обеспечивает возможность ассоциативной связи между последовательными "доминантными" состояниями сети.
Описанная модель обработки информации была названа нейрохронотопом. Функциональная схема нейрохронотопа представлена на рис. 1.
Отметим, что в рамках данной модели внимания получает объяснение ряд важных физиологических и психологических феноменов [73]. Среди них эффект селективного внимания (cocktail party effect), закон Йеркеса-Додсона (качество выполнения задания в зависимости от величины возбуждения имеет перевернутую U-образную форму), эффект интеграции стимулов (принятие решения, зависящего от комбинации стимулов, требует существенно большего времени, чем в случае одиночного стимула), Струп-эффект (время, требующееся для определения цвета чернил, которыми написано слово, существенно увеличивается, если слово обозначает цвет, отличный от того, которым оно написано).
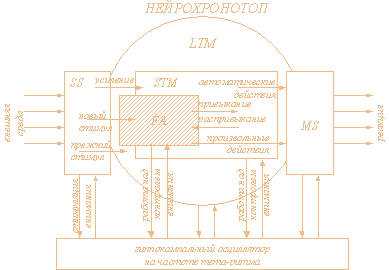
Рис.1 - Схема нейрохронотопа. SS - группа осцилляторов, на которые поступает сенсорная информация , FA - фокус внимания, STM - кратковременная память, LTM - долговременная память, MS - группа осцилляторов, обеспечивающая двигательную реакцию. STM представляет собой активную часть LTM, FA представляет собой синхронизованную с СГО часть STM, SS и MS представлены как частично активированные подмножества LTM (на это указывает пунктирная граница, отделяющая их от LTM)
