Содержание
- Нейросети второго поколения
- Глубокое обучение
- Практические эксперименты
- 3.1. Язык R
- 3.2. Варианты реализации и решаемые задачи
- 3.3. Подготовка данных для эксперимента
- 3.3.1. Исходные данные
- 3.3.2. Входные переменные (предикторы)
- 3.3.2.1. Welles Wilder's Directional Movement Index - ADX(HLC, n)
- 3.3.2.2. aroon(HL, n)
- 3.3.2.3. Commodity Channel Index - CCI(HLC, n)
- 3.3.2.4. chaikinVolatility (HLC, n)
- 3.3.2.5. Chande Momentum Oscillator - CMO(Med, n)
- 3.3.2.6. MACD oscillator
- 3.3.2.7. OsMA(Med,nFast, nSlow, nSig)
- 3.3.2.8. Relative Strength Index - RSI(Med,n)
- 3.3.2.9. Stochastic Oscillator - stoch(HLC, nFastK=14, nFastD=3, nSlowD=3)
- 3.3.2.10. Stochastic Momentum Index - SMI(HLC, n = 13, nFast = 2, nSlow = 25, nSig = 9)
- 3.3.2.11. Volatility (Yang and Zhang) - volatility(OHLC, n, calc="yang.zhang", N=96)
- 3.3.3. Выходные данные (целевая)
- 3.3.4. Очистка данных
- 3.3.5. Формирование обучающей и тестовой выборок
- 3.3.6. Балансировка классов
- 3.3.7. Препроцессинг
- 3.4. Построение, обучение и тестирование моделей
- Программная реализация (индикатор и эксперт)
Введение
В статье будут рассмотрены основные понятия по теме "Глубокое обучение" (Deep Learning), "Глубокие нейросети" (Deep Network) без сложных математических выкладок, как говорят, "на пальцах".
Будут проведены эксперименты с реальными данными подтверждающие (или нет) теоретические преимущества "глубоких сетей" перед "мелкими" путем определения и сравнения метрик. Решаемая задача — классификация. Мы создадим индикатор и эксперт, использующие модель глубокой сети и работающих в связке по схеме клиент-сервер и проведем их тестирование.
Предполагается, что читатели знакомы с основными понятиями по теме "Нейросети". Поскольку терминология по теме глубокое обучение на русском языке не установилась, будут приводиться, в необходимых случаях, термины на английском.
1. Нейросети второго поколения
Нейросети наиболее приспособлены к решению широкого круга задач, так или иначе связанных с обработкой образов.
Вот список типичных задач для нейросетей:
- Аппроксимация функций по набору точек (регрессия);
- Классификация данных по заданному набору классов;
- Кластеризация данных с выявлением заранее неизвестных классов-прототипов;
- Сжатие информации;
- Восстановление утраченных данных;
- Ассоциативная память;
- Оптимизация, оптимальное управление и др.
Из всего перечисленного в статье будем рассматривать только "Классификацию".
1.1. Архитектура связей
На способ обработки информации решающим образом сказывается наличие или отсутствие в сети петель обратных связей. Если обратные связи между нейронами отсутствуют (т.е. сеть имеет структуру последовательных слоев, где каждый нейрон получает информацию только с предыдущего слоя), обработка информации в сети однонаправлена. Входной сигнал обрабатывается последовательностью слоев, и ответ
гарантированно получается через число тактов, равному числу слоев.
Наличие же обратных связей может сделать динамику нейросети (называемой в этом случае рекуррентной) непредсказуемой. В принципе, сеть может "зациклиться" и не выдать ответа никогда. Причем, согласно Тьюрингу, не существует алгоритма, позволяющего для произвольной рекуррентной сети определить, придут ли когда-либо ее элементы в состояние равновесия (т.н. проблема останова).
Вообще говоря, то, что нейроны в рекуррентных сетях по многу раз принимают участие в обработке информации, позволяет таким сетям производить более разнообразную и глубокую обработку информации. Но в этом случае следует принимать специальные меры к тому, чтобы сеть не зацикливалась (например, использовать симметричные связи, как в сети Хопфилда, или принудительно ограничивать число итераций).
Тип обучения
Тип связей | С "учителем" | Без "учителя" |
|---|
| Без обратных связей | Многослойные персептроны (аппроксимация функций, классификация)
| Соревновательные сети, карты Кохонена (сжатие данных, выделение признаков) |
| С обратными связями | Рекуррентные аппроксиматоры (предсказание временных рядов, обучение в режиме on-line)
| Сеть Хопфилда (ассоциативная память, кластеризация данных, оптимизация) |
Таблица 1. Классификация нейросетей по типу связей и типу обучения
1.2. Основные виды нейросетей
Исторически, начавшись с перцептрона, нейросети прошли значительный путь в своем развитии. На сегодня известно и с пользой применяется большое количество нейросетей, разнообразных по структуре и методам обучения.
Из наиболее известных вспомним:
1.2.1. Многослойные полносвязные сети прямого распространения MLP (multilayer perceptron)
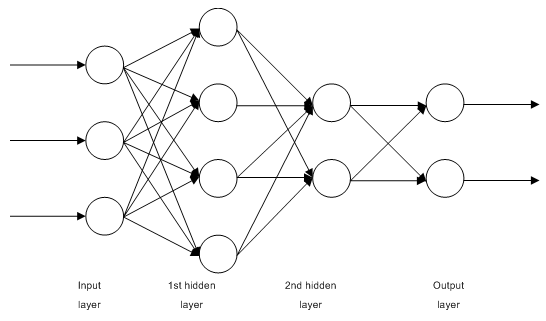
Рис. 1. Структурная схема многослойной нейросети
1.2.2. Сеть Джордана - частично рекуррентная сеть, подобна сетям Элмана (Jordan networks are partially recurrent networks and similar to Elman networks).
Ее можно рассматривать как сеть прямого распространения с дополнительными нейронами контекста во входном слое.
Эти контекстные нейроны принимают вход от себя (прямая обратная связь, direct feedback) и из выходных нейронов. Контекстные нейроны сохраняют текущее состояние сети. В сети Джордана количество контекстных и выходных нейронов должно быть одинаковым.
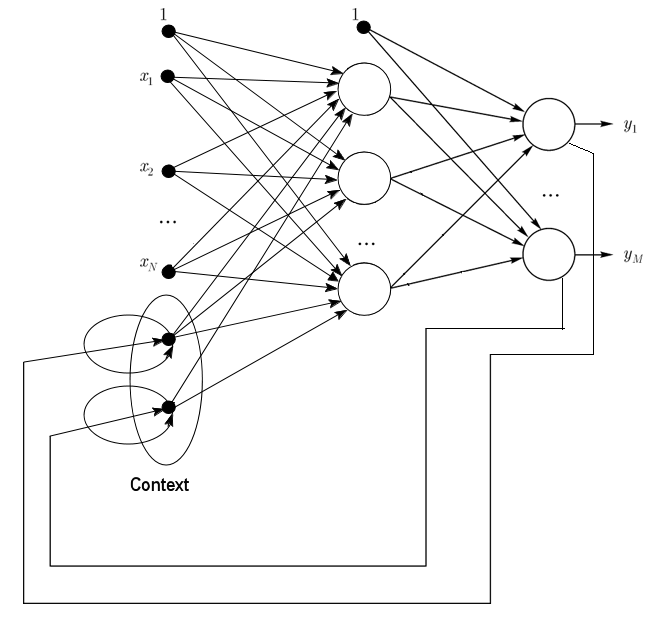
Рис. 2. Структурная схема сети Джордана
1.2.3. Сеть Элмана - частично рекуррентная сеть, подобна сетям Джордана (Elman networks are partially recurrent networks and similar to Jordan networks). Разница между сетью Элмана и Джордана
в том, что в сети Элмана контекстные нейроны берут вход не от выходных нейронов, а от скрытых. Кроме того, в контекстных нейронах нет никакой прямой обратной связи.
В сети Элмана число контекстных и скрытых нейронов должно быть одинаковым. Главное преимущество сетей Элмана состоит в том, что число контекстных нейронов определяется не размерностью выхода (как в сети Джордана) а количеством скрытых нейронов, что делает ее более гибкой. Можно легко добавить или убрать скрытые нейроны, в отличие от количества выходов.
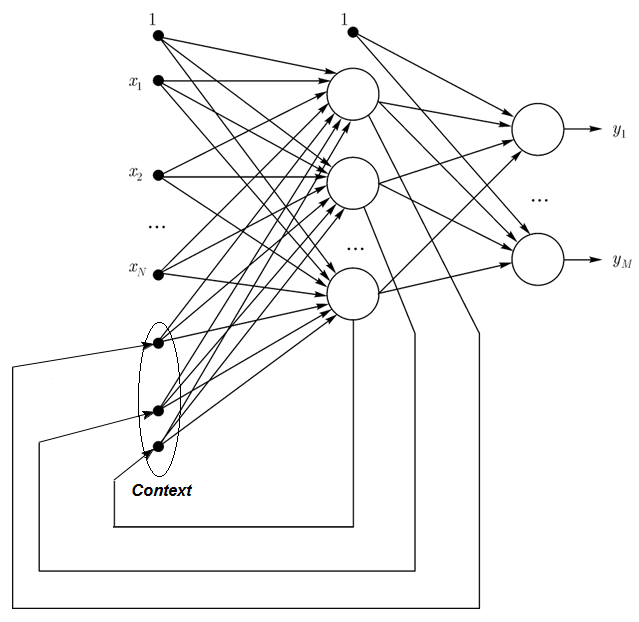
Рис. 3. Структурная схема сети Элмана
1.2.4. Сеть радиальных базисных функций (RBF) - нейронная сеть прямого распространения, которая содержит промежуточный (скрытый) слой радиально симметричных нейронов. Такой нейрон преобразовывает расстояние от данного входного вектора до соответствующего ему "центра" по некоторому нелинейному закону (обычно функция Гаусса).
Сети RBF имеют ряд преимуществ перед многослойными сетями прямого распространения. Во-первых, они моделируют произвольную нелинейную функцию с помощью всего одного промежуточного слоя, тем самым, избавляя разработчика от необходимости решать вопрос о числе слоев. Во-вторых, параметры линейной комбинации в выходном слое можно полностью оптимизировать с помощью хорошо известных методов линейной оптимизации, которые работают быстро и не испытывают трудностей с локальными минимумами, так мешающими при обучении с использованием алгоритма обратного распространения ошибки. Поэтому сеть RBF обучается очень быстро - на порядок быстрее, чем с использованием алгоритма ОР (обратного распространения).
Недостатки сетей RBF: данные сети обладают плохими экстраполирующими свойствами и получаются весьма громоздкими при большой размерности вектора входов.
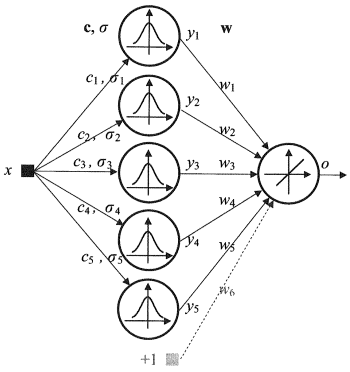
Рис. 4. Структурная схема RBF
1.2.5. Динамические сети обучаемого векторного квантования (Dynamic learning vector quantization, DLVQ networks) похожи на самоорганизующиеся карты Кохонена (SOM). В отличие от SOM, она обучается
с учителем, и в ней отсутствуют соседские отношения между прототипами (But they perform supervised learning and lack a neighborhood relationship between the prototypes). Векторное квантование является намного более общей операцией, чем кластеризация.
1.2.6. Нейронная сеть Хопфилда - полносвязная нейронная сеть с симметричной матрицей связей. В процессе работы динамика таких сетей сходится (конвергирует) к одному из положений равновесия. Эти положения равновесия являются локальными минимумами функционала, называемого энергией сети. Такая сеть может быть использована как автоассоциативная память, как фильтр, а также для решения некоторых задач оптимизации.
В отличие от многих нейронных сетей, работающих до получения ответа через определенное количество тактов, сети Хопфилда работают до достижения равновесия, когда следующее состояние сети в точности равно предыдущему: начальное состояние является входным образом, а при равновесии получают выходной образ. Обучение сети Хопфилда требует, чтобы обучающий образ был представлен на входном и выходном слоях одновременно.
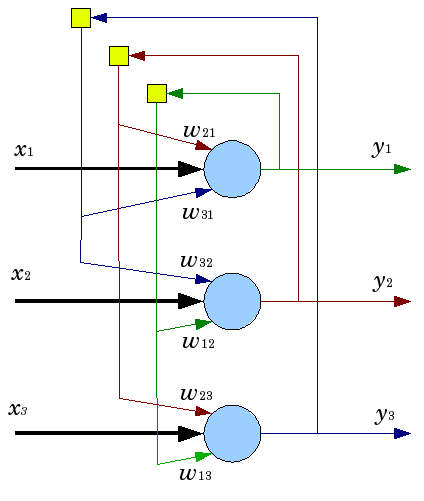
Рис. 5. Схема сети Хопфилда с тремя нейронами
Несмотря на интересные качества, нейронная сеть в классической модели Хопфилда далека от совершенства. Она обладает относительно скромным объемом памяти, приблизительно 15% от количества нейронов сети N, в то время как системы адресной памяти могут хранить до 2N различных образов, используя N битов.
Кроме того, нейронные сети Хопфилда не могут решить задачу распознавания, если изображение смещено или повернуто относительно его исходного запомненного состояния. Эти и другие недостатки сегодня определяют общее отношение к модели Хопфилда, скорее как к теоретическому построению, удобному для исследований, чем как повседневно используемому практическому средству.
И многие другие, не упомянутые здесь (Хеминга, Гросберга, сети адаптивной резонансной теории (ART-1, ART-2) и т.п.) поскольку не нашли широкого применения в нашей области интересов.
1.3. Методы обучения
Способность к обучению является основным свойством мозга. Для искусственных нейронных сетей под обучением понимается процесс настройки архитектуры сети (структуры связей между нейронами) и весов синаптических связей (влияющих на сигналы коэффициентов) для эффективного решения поставленной задачи. Обычно обучение нейронной сети осуществляется на некоторой выборке. По мере процесса обучения, который происходит по некоторому алгоритму, сеть должна все лучше и лучше (правильнее) реагировать на входные сигналы.
Выделяют три парадигмы обучения: с учителем, самообучение и смешанная. В первом способе известны правильные ответы к каждому входному примеру, а веса подстраиваются так, чтобы минимизировать ошибку. Обучение без учителя позволяет распределить образцы по категориям за счет раскрытия внутренней структуры и природы данных. При смешанном обучении комбинируются два вышеизложенных подхода.
1.3.1. Основные правила обучения нейронных сетей
Известны четыре основных правила обучения, обусловленные связанными с ними архитектурами сетей: коррекция ошибки, правило Больцмана, правило Хебба и метод соревнования.
1.3.1.1. Коррекция ошибки
Для каждого входного примера задан требуемый выход (целевой), который может не совпадать с реальным (предсказанным) значением. Правило обучения при коррекции по ошибке состоит в использовании разницы между целевой и предсказанной переменной для изменения весов, с целью уменьшения ошибки рассогласования. Обучение производится только в случае ошибочного результата. Известны многочисленные модификации этого правила обучения.
1.3.1.2. Правило Больцмана
Правило Больцмана является стохастическим правилом обучения, обусловленным аналогией с термодинамическими принципами. В результате его выполнения осуществляется настройка весовых коэффициентов нейронов в соответствии с требуемым распределением вероятностей. Обучение правилу Больцмана может рассматриваться как отдельный случай коррекции по ошибке, в котором под ошибкой понимается расхождение корреляций состояний в двух режимах.
1.3.1.3. Правило Хебба
Правило Хебба является самым известным алгоритмом обучения нейронных сетей, суть которого заключается в следующем: если нейроны с обеих сторон синапса возбуждаются одновременно и регулярно, то сила синаптической связи возрастает. Важной особенностью является то, что изменение синаптического веса зависит только от активности связанных этим синапсом нейронов. Предложено большое количество разновидностей этого правила, различающихся особенностями модификации синаптических весов.
1.3.1.4. Метод соревнования
В отличие от правила Хебба, в котором множество выходных нейронов могут возбуждаться одновременно, здесь выходные нейроны соревнуются между собой. И выходной нейрон с максимальным значением взвешенной суммы является "победителем" ("победитель забирает все"). Выходы же остальных выходных нейронов устанавливаются в неактивное состояние. При обучении модифицируются только веса нейрона - "победителя" в сторону увеличения близости к данному входному примеру.
Существует большое число алгоритмов обучения, ориентированных на решение разных задач. Среди них выделяется алгоритм обратного распространения ошибки, который является одним из наиболее успешных современных алгоритмов. Его основная идея заключается в том, что изменение весов синапсов происходит с учетом локального градиента функции ошибки.
Разница между реальными и правильными ответами нейронной сети, определяемыми на выходном слое, распространяется в обратном направлении (рис.5) — навстречу потоку сигналов. В итоге каждый нейрон способен определить вклад каждого своего веса в суммарную ошибку сети. Простейшее правило обучения соответствует методу наискорейшего спуска, то есть изменения синаптических весов пропорционально их вкладу в общую ошибку.
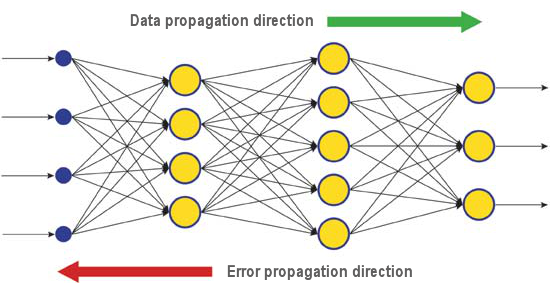
Рис. 6. Схема распространения данных и ошибки в нейросети при обучении методом обратного распространения ошибки
Конечно, при таком обучении нейронной сети нет уверенности, что она обучилась наилучшим образом, поскольку всегда существует возможность попадания алгоритма в локальный минимум. Для этого используются специальные приемы, позволяющие "выбить" найденное решение из локального экстремума. Если после нескольких таких действий нейронная сеть сходится к тому же решению, то можно сделать вывод о том, что найденное решение, скорее всего, оптимально.
1.4. Недостатки
- Основная трудность использования нейросетей - так называемое "проклятие размерности". При увеличении размерности входов и количества слоев, сложность сети и соответственно время обучения растет экспоненциально, при этом полученный результат далеко не оптимальный.
- Другая трудность использования нейронных сетей состоит в том, что традиционные нейронные сети неспособны объяснить, каким образом они решают задачу. Для многих областей это объяснение более важно, чем сам результат (например, медицина). Внутреннее представление результатов обучения зачастую настолько сложно, что его невозможно проанализировать, за исключением некоторых простейших случаев, обычно не представляющих интереса.
2. Глубокое обучение
В настоящее время теория и практика машинного обучения переживают настоящую "глубинную революцию", вызванную успешным применением методов Deep Learning (глубокого обучения), представляющих собой третье поколение нейронных сетей. В отличие от классических (второго поколения) нейронных сетей 80–90-х годов прошлого века, новые парадигмы обучения позволили избавиться от ряда проблем, которые сдерживали распространение и успешное применение традиционных нейронных сетей.
Сети, обученные с помощью алгоритмов глубокого обучения, не просто превзошли по точности лучшие альтернативные подходы, но и в ряде задач проявили зачатки понимания смысла подаваемой информации (например, при распознавании изображений, анализе текстовой информации и так далее).
Наиболее успешные современные промышленные методы компьютерного зрения и распознавания речи построены на использовании глубоких сетей, а гиганты IT-индустрии, такие как Apple, Google, Facebook, скупают коллективы исследователей, занимающихся глубокими нейросетями.
2.1. Немного истории
Команда аспирантов из университета г. Торонто (Канада) под руководством профессора Джеффри Хинтона (Geoffrey E. Hinton), выиграла конкурс, проводимый фармацевтической компанией Merck. Имея в своем распоряжении ограниченный набор данных, описывающих химическую структуру 15 молекул, группа Хинтона сумела создать и использовать специальную программную систему, которая определила, какая из этих молекул будет эффективнее других работать в качестве лекарства.
Особенность этой работы заключается в том, что разработчики системы использовали искусственную нейронную сеть на базе так называемого "глубокого обучения" (Deep Learning). В итоге их система смогла провести нужные расчеты и исследования на основании крайне малого набора исходных данных: обычно для обучения нейронных сетей перед использованием требуется загрузить в систему просто огромный массив информации.
Достижение команды Хинтона выглядит особенно впечатляющим, если учесть, что заявка на участие была подана буквально в последний момент. Более того, сама система "глубокого обучения" создавалась в условиях отсутствия конкретных данных о взаимодействии предложенных молекул с целевыми объектами. Успешное применение методики "глубокого обучения" стало еще одним достижением в развитии
искусственного интеллекта, которыми очень богата вторая половина 2012 года.
Так, летом этого года Джефф Дин (Jeff Dean) и Эндрю Нг (Andrew Y. Ng) из Google показали новую систему для распознавания изображений с точностью определения кота на снимке 15,8%, где для обучения кластерной системы из 16 тысяч узлов использовалась сеть ImageNet, содержащая 14 миллионов образов 20 тысяч разных объектов. В прошлом году швейцарские ученые показали систему, которая лучше человека распознавала дорожные знаки на фотографиях (точность составила 99,46% на наборе из 50 000 картинок, причем у людей максимальная точность составила 99,22%, а средняя точность по группе из 32 человек составила "всего" 98,84%). Наконец, в октябре этого года Ричард Рашид (Richard F. Rashid), координатор научных программ Microsoft, показал на конференции в Тяньцзине (КНР) технологию живого перевода с английского на мандаринский китайский с сохранением исходного голоса.
Все эти технологии, демонстрирующие прорыв в области искусственного интеллекта, в той или иной мере опираются на методику "глубокого обучения". Главный вклад в теорию глубокого обучения сейчас вносит как раз профессор Хинтон, который, кстати, является праправнуком Джорджа Буля, английского ученого, изобретателя булевой алгебры, лежащей в основе современных вычислительных машин.
Теория глубокого обучения дополняет обычные технологии машинного обучения специальными алгоритмами для анализа входной информации на нескольких уровнях представления. Особенность нового подхода заключается в том, что "глубокое обучение" изучает предмет, пока не найдет достаточно информативных уровней представления для учета всех факторов, способных повлиять на характеристики изучаемого предмета.
Таким образом, нейронная сеть на базе такого подхода требует меньше входной информации для обучения, а обученная сеть способна анализировать информацию с гораздо более высокой точностью, чем обычные нейронные сети. Сам Хинтон с коллегами заявляют, что их технология особенно хорошо подходит для поиска особенностей в многомерных, хорошо структурированных массивах информации.
Технологии искусственного интеллекта (ИИ) вообще, и глубокое обучение в частности, сейчас широко применяются в разных системах, включая голосового помощника Apple Siri на базе технологий Nuance Communications и распознавание адресов в службе Просмотра улиц Google. Тем не менее, ученые очень осторожно оценивают успехи в данной области, поскольку история создания ИИ изобилует громкими обещаниями и не менее громкими спадами.
Так, в 1960-х годах ученые считали, что до создания полноценного ИИ осталось всего около 10 лет. Потом, в 1980-х, была целая волна молодых компаний, предлагавших "готовый ИИ", после чего в этой области наступил настоящий "ледниковый период" — вплоть до нынешнего времени, когда огромные вычислительные возможности, доступные в облачных сервисах, открыли новый уровень для реализации мощных нейронных сетей с использованием новой теоретической и алгоритмической базы.
Стоит отдельно заметить, что нейронные сети (даже третьего поколения, такие как сверточные сети, авто-кодировщики, глубинные машины Больцмана) не имеют ничего общего с биологическими нейронами, кроме названия.
Новая парадигма обучения реализует идею обучения в два этапа. На первом этапе из большого массива неразмеченных данных с помощью автоассоциаторов (путем их послойного обучения без учителя) извлекается информация о внутренней структуре входных данных. Затем, используя эту информацию в многослойной нейросети, ее обучают с учителем (размеченными данными) известными методами. При этом количество неразмеченных данных желательно иметь как можно большим. Размеченных данных может быть намного меньше. Для нашего случая это не очень актуально.
2.2. Автоассоциаторы. Автоэнкодер и ограниченная машина Больцмана. Отличия и особенности
2.2.1. Автоэнкодер
Первым автоассоциатором (АА) был неокогнитрон Фукушимы.
Схема приведена на рис.7.
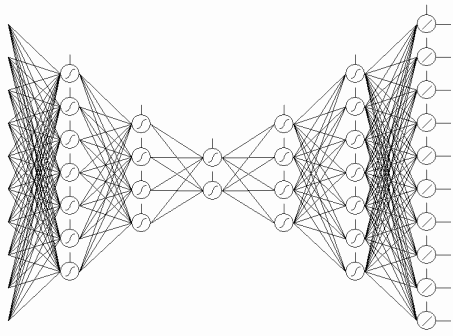
Рис. 7. Неокогнитрон Фукушимы
Задача АвтоАссоциатора (АА) получить на выходе как можно более точное отображение входа.
Используются два вида АА — генерирующие и синтезирующие. В качестве первых используют ограниченные машины Больцмана (Restricted Boltzmann Machine, RBM) а вторых — автоэнкодеры (АE).
Автоэнкодер — нейросеть с одним скрытым слоем, которая применяя алгоритм обучения без учителя и метод обратного распространения ошибки устанавливает целевое значение, равное входному вектору, т.е. y = x.
Пример Автоэнкодера приведен на рис.8.
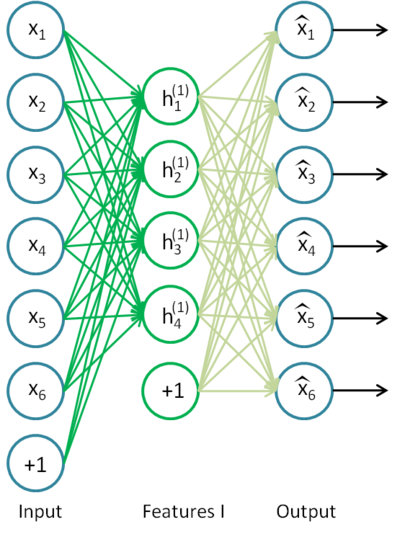
Рис. 8. Структурная схема Автоэнкодера
Автоэнкодер пытается построить функцию h(x)=x. Другими словами, пытается найти аппроксимацию такой функции, чтобы отклик нейронной сети приблизительно равнялся значению входных признаков. Для того, чтобы решение этой задачи было нетривиальным количество нейронов скрытого слоя должно быть меньше, чем размерность входных данных (как на рисунке).
Это позволяет получить сжатие данных при передаче входного сигнала на выход сети. Например, если входной вектор представляет собой набор уровней яркости изображения 10х10 пикселов (всего 100 признаков), а количество нейронов скрытого слоя 50, сеть вынужденно обучается компрессии изображения. Ведь требование h(x)=x означает, что исходя из уровней активации пятидесяти нейронов скрытого слоя выходной слой должен восстановить 100 пикселей исходного изображения. Такая компрессия возможна, если в данных есть скрытые взаимосвязи, корреляция признаков, и вообще какая-то структура. В таком виде функционирование автоэнкодера очень напоминает метод анализа главных компонент (PCA) в том смысле, что понижается размерность входных данных.
Удивительно, но эксперименты, о которых сообщали Bengio и др. (2007), показали, что при обучении со стохастическим градиентным спуском нелинейные автокодирующие устройства с количеством скрытых нейронов большим, чем входов (названные сверхполными), выдали полезные представления (в смысле аттестационной ошибки, измеренной на сети, берущей это представление во входе).
Позже с появлением идеи разрежения (sparsity) получил распространение разреженный Автоэнкодер (sparse Autoencoder).
Разреженный Автоэнкодер - это Автоэнкодер, у которого количество скрытых нейронов гораздо больше размерности входа, но они имеют разреженную активацию. Разреженная активация – это когда количество неактивных нейронов в скрытом слое значительно превышает количество активных. Если описывать разреженность неформально, то будем считать нейрон активным, когда значение его функции передачи близко к 1. Если используется сигмоидная функция передачи, то для неактивного нейрона ее значение должно быть близко к 0 (для функции гиперболического тангенса – к -1).
Существует вариант автокодирующего устройства, называемый denoising Автоэнкодер (Винсент и др., 2008). Это тот же Автоэнкодер, но обучение его специфично. При обучении на вход подают случайным образом "испорченные" данные (заменяют некоторые значения на 0). При этом для сравнения с выходом предъявляют "неиспорченные". Таким способом можно заставить автоэнкодер восстанавливать поврежденные входные данные.
2.2.2. Ограниченная машина Больцмана (Restricted Boltzmann Machine, RBM).
Я не буду особо заострять внимание на истории происхождения ограниченной машины Больцмана (RBM), упомяну лишь, что началось все с рекуррентных нейросетей, которые представляют из себя сети с обратной связью и которые крайне трудно обучить. Вследствие этого небольшого затруднения в обучении, народ стал выдумывать более ограниченные рекуррентные модели, для которых можно было бы применить более простые алгоритмы
обучения. Одной из таких моделей была нейронная сеть Хопфилда, и он же ввел понятие энергии сети, сравнив нейросетевую динамику с термодинамикой.
Следующим шагом на пути к RBM были обыкновенные машины Больцмана, они отличаются от сети Хопфилда тем, что имеют стохастическую природу, а нейроны поделены на две группы, описывающие видимые и скрытые
состояния (по аналогии со скрытыми моделями Маркова). Ограниченная машина Больцмана отличается от обыкновенной отсутствием связей между нейронами одного слоя.
На рис. 9 приведена структурная схема RBM.
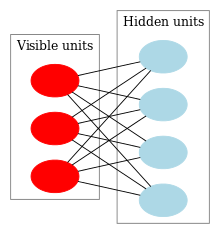
Рис. 9. Структурная схема RBM
Особенность этой модели в том, что при данном состоянии нейронов одной группы, состояния нейронов другой группы будут независимы друг от друга. Теперь можно перейти к немножко теории, где ключевую роль играет именно это свойство.
Интерпретация и цель
RBM интерпретируются аналогично скрытым моделям Маркова. У нас есть ряд состояний, которые мы можем наблюдать (видимые нейроны) и ряд состояний, которые скрыты, и мы не можем напрямую увидеть их состояние (скрытые нейроны). Но мы можем сделать вероятностный вывод относительно скрытых состояний, опираясь на состояния, которые мы можем наблюдать. Обучив такую модель мы так же получаем возможность делать выводы относительно видимых состояний, зная скрытые (теорему Байеса никто не отменял =), и тем самым генерировать данные из того вероятностного распределения, на котором обучена модель.
Таким образом, мы можем сформулировать цель обучения модели: необходимо настроить параметры модели так, чтобы восстановленный вектор из исходного состояния был наиболее близок к оригиналу. Под восстановленным понимается вектор, полученный вероятностным выводом из скрытых состояний, которые в свою очередь получены вероятностным выводом из видимых состояний, т.е. из оригинального вектора.
Алгоритм обучения - Сравнительное расхождение (сопоставительное отклонение) (Contrastive Divergence CD-k)
Этот алгоритм придуман профессором Хинтоном в 2002 году, и он отличается своей простотой. Главная идея в том, что математические ожидания заменяются вполне определенными значениями. Вводится понятие процесса
сэмплирования (Gibbs sampling).
Процесс CD-k выглядит следующим образом:
- Состояние видимых нейронов приравнивается к входному образу;
- Выводятся вероятности состояний скрытого слоя;
- Каждому нейрону скрытого слоя ставится в соответствие состояние "1" с вероятностью, равной его текущему состоянию;
- Выводятся вероятности видимого слоя на основании скрытого слоя;
- Если текущая итерация меньше k, то возврат к шагу 2;
- Выводятся вероятности состояний скрытого слоя;
В лекциях у Хинтона это выглядит так:
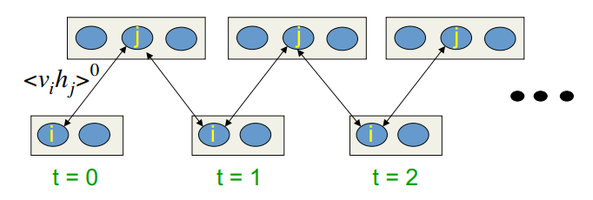
Рис.10. Алгоритм обучения CD-k
Т.е. чем дольше мы делаем сэмплинг, тем точнее будет наш градиент. В то же время профессор утверждает, что даже для CD-1 (всего одна итерация сэмплинга) уже вполне хороший результат получается.
2.3. Накапливающие автоассоциативные сети (stacked autoassociators network). Накапливающие автоэнкодеры (Stackеd Autoencoder SAE), Накапливающие сети Больцмана (Stacked RBM)
Для извлечения из входного набора данных абстракций высокого уровня автоассоциаторы складывают в сеть.
На рис. 11 приведена структурная схема накапливающего автоэнкодера и нейросети, которые в совокупности и представляют собой Глубокую нейросеть с инициализацией весов от SAE ("Deep neural network with weights initialized by Stacked AutoEncoder")
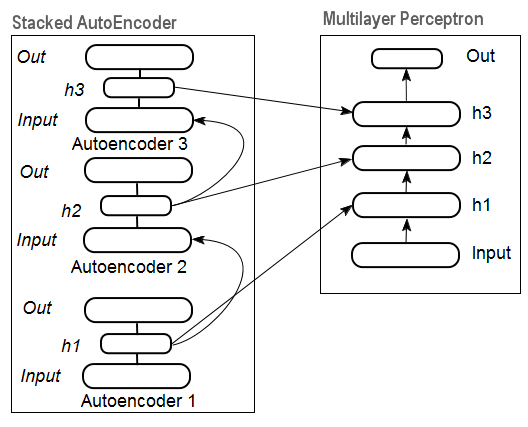
Рис. 11. Структурная схема DN SAE
На рис.12 приведена схема накапливающей RBM (SRBM) и нейросети, которые в совокупности представляют собой Глубокую нейросеть с инициализацией весов от SRBM ("Deep neural network with weights initialized by SRBM").
Схемы глубоких сетей изображают именно таким образом, подчеркивая, что информация извлекается снизу вверх.
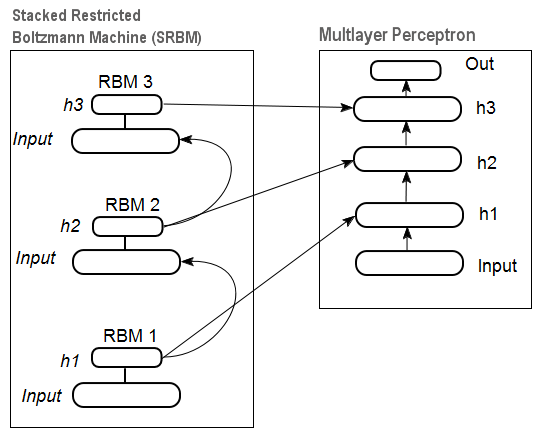
Рис. 12. Структурная схема DN SRBM
2.4. Обучение глубоких сетей (DN). Этапы обучения. Особенности
Обучение глубоких сетей проводят в два этапа. На первом этапе послойно обучают без учителя на массиве не размеченных данных автоассоциативную сеть (SAE или SRBM, в зависимости от типа DN), после чего
полученными после обучения весами скрытых слоев автоассоциативной сети инициализируют нейроны скрытых слоев обычной MLP. На рис. 11 и рис. 12 схематично показан этот процесс обучения и переноса. После обучения
первого АЕ/RBM веса нейронов скрытого слоя становятся входами второго и так далее. Тем самым из данных извлекается все более обобщающая информация о структуре (линия, контур, образ и т.д).
На втором этапе происходит тонкая настройка MLP (обучение с учителем) на размеченном наборе данных общеизвестными методами. Практически доказано, что такая инициализация устанавливает веса нейронов скрытых слоев MLP в область глобального минимума и последующая тонкая настройка происходит за очень короткое время.
Кроме того для глубоких сетей с количеством слоев более трех Д.Хинтон предложил тонкую настройку производить также в два этапа. На первом обучать только два верхних слоя и только потом обучать всю сеть.
Необходимо отметить, что при обучении без учителя SRBM дает менее стабильные результаты, чем SAE.
Замечание. Часто в литературе происходит путаница с терминами. SRBM отождествляют с глубокими сетями доверия (Deep belief network DBN). Несмотря на то, что RBM произошли от DBN, это
кардинально разные структуры. DBN это многослойная нейросеть, у которой веса нейронов скрытых слоев инициализируют случайным образом бинарными образцами.
3. Практические эксперименты
Реализацию глубоких сетей будем осуществлять на языке R.
3.1. Язык R
Немного истории. R является языком программирования (а также средой для статистических вычислений и построения графиков), который был разработан в 1996 году новозеландскими учеными Россом Ихака и Робертом Джентельменом при университете Окленда.
R является GNU-проектом, то есть свободным программным обеспечением, философия использования которого сводится к следующим принципам, а точнее свободам:
- свобода запускать программы в любых целях (свобода 0);
- свобода изучать, как работает программа, и адаптировать ее под свои нужды (свобода 1);
- свобода распространять копии, чтобы помочь своему ближнему (свобода 2);
- свобода улучшать программу и делать ваши улучшения общедоступными к выгоде всего сообщества.
В исторической перспективе R представляет альтернативную реализацию языка программирования S. Последний был разработан в компании Bell Labs Джоном Чемберсом и его коллегами в 1976 году. В данный момент R продолжает улучшаться усилиями "R Development Core Team", членом которой также является и Д.Чемберс.
Для повторения экспериментов вам необходимо будет установить язык R и Rstudio. О том, как установить и где взять, в русскоязычной сети и в приложениях достаточно информации. Если возникнут вопросы, обсудим дополнительно при обсуждении статьи.
Преимущества языка R:
- На сегодняшний день язык R де-факто является стандартом в статистических вычислениях.
- Развивается и поддерживается мировым научным сообществом университетов мира.
- Широчайший набор пакетов по всем передовым направлениям интеллектуального анализа данных (Data mining). Причем от появления новой идеи в научных публикациях до их реализации в пакете R проходит не более 2 недель.
- Последнее по порядку, но не по значению - он абсолютно бесплатный. Как говорил один известный разработчик свободной ОС: "Программы — как секс: лучше, когда это бесплатно".
3.2. Варианты реализации и решаемые задачи
Возможны два варианта практической реализации.
Первый - использовать авторские программы Д.Хинтона для Матлаба. Для чего нужно использовать пакет "R.matlab". Пакет предоставляет методы writeMat() и readMat() для чтения и записи MAT файлов. Это дает возможность коммуникации (выполнять код, отправлять и получать объекты и т.п.) с Matlab v6 или выше, запущенным локально или на удаленном хосте в связке клиент-сервер.
С деталями можно ознакомиться в описании пакета. Этот путь для тех у кого имеется Matlab и он с ним на ты. Я не ходил этим путем, но о возможности таким образом связать Matlab и MQL могу сообщить.
Второй — использовать пакеты языка R по этой теме. Вот этот путь мы и будем использовать.
По теме статьи "глубокие нейросети" мне известны три пакета:
"deepnet" - простой пакет, реализующий модель DN SAE и DN SRBM. Длина набора входных данных при обучении без учителя и с учителем одинакова. Нет возможности провести тонкую настройку в два этапа. Для освоения и опробования моделей на начальном этапе.
"darh" - очень развитый и широкий пакет моделирования для DN SRBM. Для DN SAE есть модель, но мне ее не удалось запустить. Этот пакет для тех, кто в теме, он позволяет создать и настроить модель любой сложности. Построен на базе оригинальных программ Хинтона на языке m для MatLab.
"H2O" - очень серьезный пакет, предназначен для обучения моделей глубоких сетей (и не только) на "больших наборах данных" (>1 Гб) записанных в csv-файлах.
В дальнейших экспериментах будем использовать пакет "deepnet".
3.3. Подготовка данных для экспериментов (входных и целевых)
Сегодня в "Интеллектуальном анализе данных" (Data mining) установился определенный порядок работы:
- Выбор исходных данных (изучение, анализ, предподготовка, оценка). Разбивка на тренировочный, валидационный и тестовый наборы (выборки);
- Обучение модели на обучающей выборке и выбор модели/моделей на валидационной;
- Оценка качества модели/моделей на тестовой выборке и определение оптимальных параметров модели или лучшей модели из набора по конкретным метрикам;
- Передача модели/моделей в работу.
Первый пункт наиболее трудоемок, но и наиболее важен для конечного результата. Справедливости ради нужно сказать, что этот пункт не формализован и по большому счету почти искусство. Многое зависит
от опыта исследователя. Но! Получить количественные оценки входного набора для выбора наиболее важных, а еще лучше автоматический выбор лучших переменных для конкретной модели просто необходимо. Так вот R предоставляет нам обширный функционал для решения задач на всех этих этапах.
Тема "Исходные данные" не только чрезвычайно важна, но и очень обширна. Заслуживает отдельной статьи. Поскольку задача настоящей статьи рассказать как можно проще о сложном, мы не будем глубоко копать, но на важные моменты будем обращать внимание.
3.3.1. Исходные данные
Для нашей задачи "Классификация" нужен набор независимых (входных) переменных и целевая переменная. Поскольку основным декларируемым преимуществом глубоких сетей является их способность быстро обучаться на входных выборках большой размерности, создадим набор входных данных из 17 предикторов (11 индикаторов) и в качестве целевой будем использовать ZigZag. В окружение R загрузим векторы котировок Open,
High, Low, Close глубиной 4000 баров. Как это сделать, будем обсуждать далее при написании индикатора. Сейчас это не важно. Все дальнейшие вычисления будут производиться в R.
Соберем в матрицу эти 4 вектора плюс среднюю цену и величину тела бара. Оформим как функцию:
pr.OHLC <- function (o, h, l, c)
{
#Объединим векторы котировок в матрицу, предварительно их развернув
#Индексация векторов таймсерий в R начинается с 1.
#Направление индексации- от старых к новым.
price <- cbind(Open = rev(o), High = rev(h), Low = rev(l), Close = rev(c))
Med <- (price[, 2] + price[, 3])/2
CO <- price[, 4] - price[, 1]
#добавим в матрицу Med и CO
price <- cbind(price, Med, CO)
}
Посмотрим, что получилось (состояние на момент 08.10. 14 12:00)
> head(price)
Open High Low Close Med CO
[1,] 1.33848 1.33851 1.33824 1.33844 1.338375 -4e-05
[2,] 1.33843 1.33868 1.33842 1.33851 1.338550 8e-05
[3,] 1.33849 1.33862 1.33846 1.33859 1.338540 1e-04
[4,] 1.33858 1.33861 1.33856 1.33859 1.338585 1e-05
[5,] 1.33862 1.33868 1.33855 1.33855 1.338615 -7e-05
[6,] 1.33853 1.33856 1.33846 1.33855 1.338510 2e-05
3.3.2. Входные переменные (предикторы)
Перечислим индикаторы. Индикаторы выбраны без всякого предпочтения, случайно с целью получить максимальную размерность входов.
Расчет всех индикаторов производится по пакету "TTR", в котором приведены многочисленные индикаторы.
3.3.2.1. Welles Wilder's Directional Movement Index - ADX(HLC, n) - 4 out (Dip, Din,DX, ADX)
Вычислим и посмотрим, как он выглядит на первых 200 барах:
> library(TTR)
> adx<-ADX(price, n = 16)
> plot.ts(head(adx, 200))
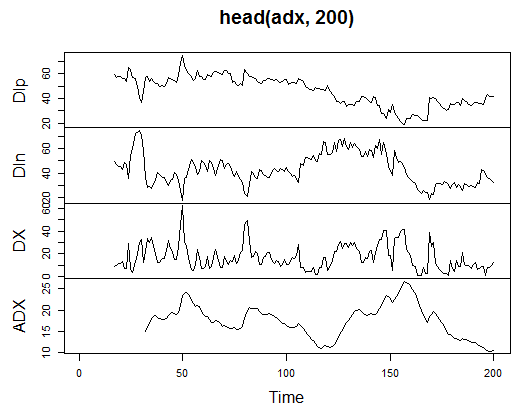
Рис. 13. Индикатор Welles Wilder's Directional Movement Index - ADX(HLC, n)
> summary(adx)
DIp DIn DX ADX
Min. :15.90 Min. : 5.468 Min. : 0.00831 Min. : 5.482
1st Qu.:41.21 1st Qu.: 33.599 1st Qu.: 8.05849 1st Qu.:14.046
Median :47.36 Median : 43.216 Median :16.95423 Median :18.099
Mean :47.14 Mean : 46.170 Mean :19.73032 Mean :19.609
3rd Qu.:53.31 3rd Qu.: 55.315 3rd Qu.:27.97471 3rd Qu.:23.961
Max. :80.12 Max. :199.251 Max. :81.08751 Max. :52.413
NA's :16 NA's :16 NA's :16 NA's :31
Как видно, в начале матрицы есть 31 неопределенное значение (NA). Далее проведем те же расчеты по всем индикаторам без подробных пояснений.
3.3.2.2. aroon(HL, n) - 1 out (oscillator)
Вычислим и посмотрим первые 200 баров только одной переменной - 'oscillator'
> ar<-aroon(price[ , c('High', 'Low')], n = 16)[ ,'oscillator']
> plot(head(ar, 200), t = "l")
> abline(h = 0)
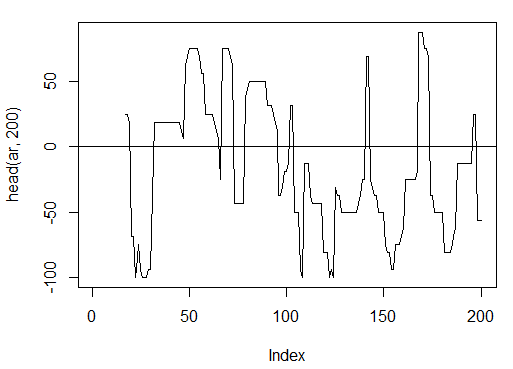
Рис. 14. Индикатор aroon(HL, n)
> summary(ar)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
-100.00 -56.25 -18.75 -7.67 43.75 100.00 16
3.3.2.3. Commodity Channel Index - CCI(HLC, n) - 1 out
> cci<-CCI(price[ ,2:4], n = 16)
> plot.ts(head(cci, 200))
> abline(h = 0)
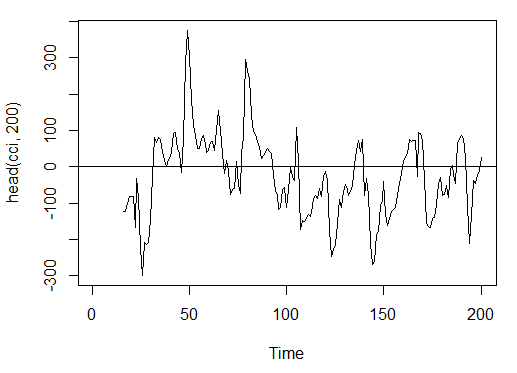
Рис. 15. Индикатор Commodity Channel Index - CCI(HLC, n)
> summary(cci)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
-469.10 -90.95 -18.74 -14.03 66.91 388.20 15
3.3.2.4. Chaikin Volatility - chaikinVolatility (HLC, n) - 1 out
> chv<-chaikinVolatility(price[ , 2:4], n = 16)
> summary(chv)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
-0.67570 -0.29940 0.02085 0.12890 0.41580 5.15700 31
> plot(head(chv, 200), t = "l")
> abline(h = 0)
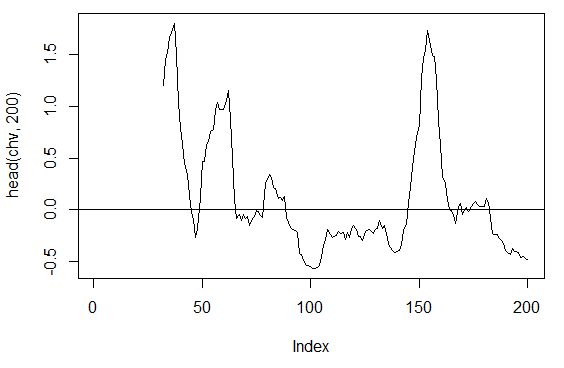
Рис. 16. Индикатор chaikinVolatility (HLC, n)
3.3.2.5. Chande Momentum Oscillator - CMO(Med, n) - 1 out
> cmo<-CMO(price[ ,'Med'], n = 16)
> plot(head(cmo, 200), t = "l")
> abline(h = 0)
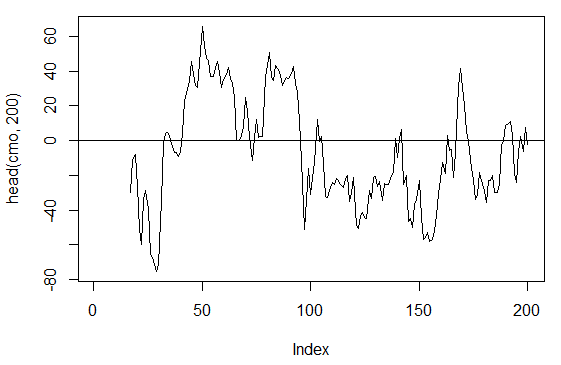
Рис. 17. Индикатор Chande Momentum Oscillator - CMO(Med, n)
> summary(cmo)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
-97.670 -32.650 -5.400 -6.075 19.530 93.080 16
3.3.2.6. MACD oscillator - MACD(Med, nFast, nSlow, nSig) будем использовать только 1 out (macd)
> macd<-MACD(price[ ,'Med'], 12, 26, 9)[ ,'macd']
> plot(head(macd, 200), t = "l")
> abline(h = 0)
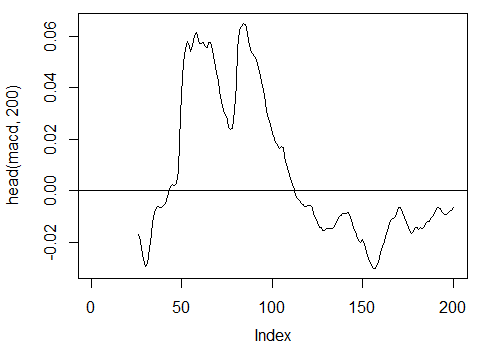
Рис. 18. Индикатор MACD oscillator
> summary(macd)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
-0.346900 -0.025150 -0.005716 -0.011370 0.013790 0.088880 25
3.3.2.7. OsMA(Med,nFast, nSlow, nSig) – 1 out
> osma<-macd - MACD(price[ ,'Med'],12, 26, 9)[ ,'signal']
> plot(head(osma, 200), t = "l")
> abline(h = 0)
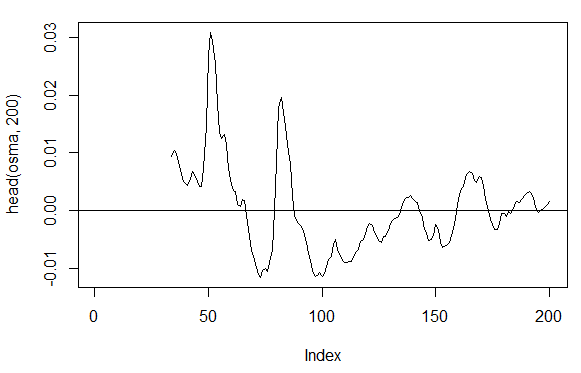
Рис. 19. Индикатор OsMA(Med,nFast, nSlow, nSig)
> summary(osma)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
-0.10560 -0.00526 0.00034 0.00007 0.00646 0.05922 33
3.3.2.8. Relative Strength Index - RSI(Med,n) – 1 out
> rsi<-RSI(price[ ,'Med'], n = 16)
> plot(head(rsi, 200), t = "l")
> abline(h = 50)
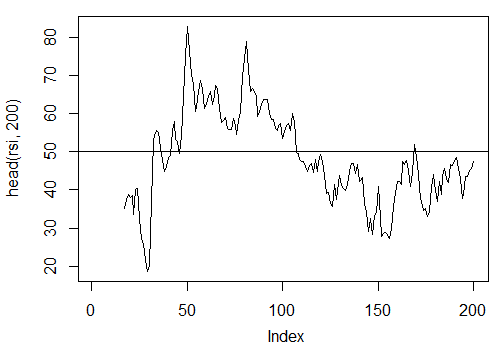
Рис. 20. Индикатор Relative Strength Index - RSI(Med,n)
> summary(rsi)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
5.32 37.33 47.15 46.53 55.71 84.82 16
3.3.2.9. Stochastic Oscillator - stoch(HLC, nFastK=14, nFastD=3, nSlowD=3) - 3 out
> stoh<-stoch(price[ ,2:4], 14, 3, 3)
> plot.ts(head(stoh, 200))
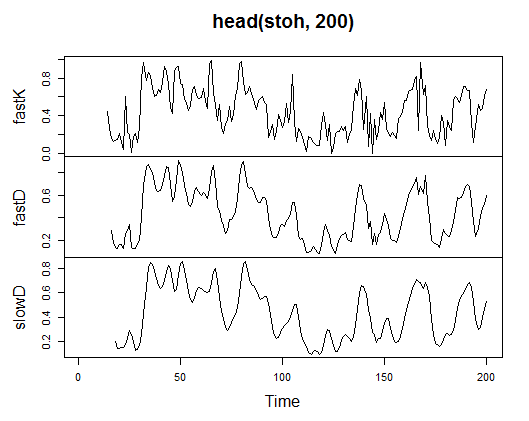
Рис. 21. Индикатор Stochastic Oscillator - stoch(HLC, nFastK=14, nFastD=3, nSlowD=3)
> summary(stoh)
fastK fastD slowD
Min. :0.0000 Min. :0.01782 Min. :0.02388
1st Qu.:0.2250 1st Qu.:0.23948 1st Qu.:0.24873
Median :0.4450 Median :0.44205 Median :0.44113
Mean :0.4622 Mean :0.46212 Mean :0.46207
3rd Qu.:0.6842 3rd Qu.:0.67088 3rd Qu.:0.66709
Max. :1.0000 Max. :0.99074 Max. :0.97626
NA's :13 NA's :15 NA's :17
3.3.2.10. Stochastic Momentum Index - SMI(HLC, n = 13, nFast = 2, nSlow = 25, nSig = 9) — 2 out
> smi<-SMI(price[ ,2:4],n = 13, nFast = 2, nSlow = 25, nSig = 9)
> plot.ts(head(smi, 200))
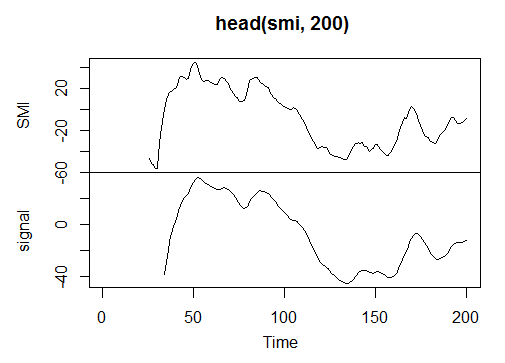
Рис. 22. Индикатор Stochastic Momentum Index - SMI(HLC, n = 13, nFast = 2, nSlow = 25, nSig = 9)
> summary(smi)
SMI signal
Min. :-82.185 Min. :-78.470
1st Qu.:-33.392 1st Qu.:-31.307
Median : -9.320 Median : -8.839
Mean : -8.942 Mean : -8.985
3rd Qu.: 15.664 3rd Qu.: 14.069
Max. : 71.878 Max. : 63.865
NA's :25 NA's :33
3.3.2.11. Volatility (по Yang and Zhang) - volatility(OHLC, n, calc="yang.zhang", N=96)- 1 out
> vol<-volatility(price[ ,1:4],n = 16,calc = "yang.zhang", N =96)
> plot.ts(head(vol, 200))
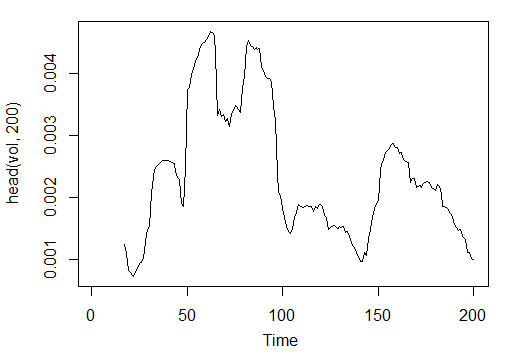
Рис. 23. Индикатор Volatility (Yang and Zhang) - volatility(OHLC, n, calc="yang.zhang", N=96)
> summary(vol)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
0.000599 0.001858 0.002638 0.003127 0.004015 0.012840 16
Итак, у нас есть 17 переменных из 11 индикаторов на символе EURUSD таймфрейм М15 на выборке OHLC глубиной 4000 баров.
Соберем их в матрицу и запишем все вышеприведенные расчеты одной функцией с одним формальным параметром р, который нам понадобится при проведении оптимизации.
Вычислим матрицу входных переменных с помощью формулы:
In<-function(p = 16){
adx<-ADX(price, n = p);
ar<-aroon(price[ ,c('High', 'Low')], n=p)[ ,'oscillator'];
cci<-CCI(price[ ,2:4], n = p);
chv<-chaikinVolatility(price[ ,2:4], n = p);
cmo<-CMO(price[ ,'Med'], n = p);
macd<-MACD(price[ ,'Med'], 12, 26, 9)[ ,'macd'];
osma<-macd - MACD(price[ ,'Med'],12, 26, 9)[ ,'signal'];
rsi<-RSI(price[ ,'Med'], n = p);
stoh<-stoch(price[ ,2:4],14, 3, 3);
smi<-SMI(price[ ,2:4],n = p, nFast = 2, nSlow = 25, nSig = 9);
vol<-volatility(price[ ,1:4],n = p,calc="yang.zhang", N=96);
In<-cbind(adx, ar, cci, chv, cmo, macd, osma, rsi, stoh, smi, vol);
return(In)
}
> X<-In()
> tail(X)
DIp DIn DX ADX ar cci chv
[3995,] 46.49620 36.32411 12.28212 18.17544 25.0 168.0407 0.1835102
[3996,] 52.99009 31.61164 25.26952 18.61882 37.5 227.7030 0.3189822
[3997,] 58.11948 28.16241 34.72000 19.62515 37.5 145.2337 0.3448520
[3998,] 56.00323 30.48687 29.50206 20.24245 37.5 118.5831 0.3068059
[3999,] 55.96197 28.78737 32.06467 20.98134 37.5 116.5376 0.3517668
[4000,] 54.97777 26.85440 34.36713 21.81795 62.5 160.0767 0.6169701
cmo macd osma rsi fastK
[3995,] 29.71342 -0.020870825 0.01666593 52.91932 0.8832685
[3996,] 41.89526 -0.009654368 0.02230591 61.49793 0.8833819
[3997,] 30.98237 -0.002051532 0.02392699 58.94513 0.7259475
[3998,] 33.84813 0.003454534 0.02354645 58.00549 0.7930029
[3999,] 38.84892 0.009590136 0.02374564 60.63806 0.8367347
[4000,] 54.71698 0.019303110 0.02676689 66.64815 0.9354120
fastD slowD SMI signal vol
[3995,] 0.7773581 0.7735064 -35.095406 -47.27712 0.003643196
[3996,] 0.7691688 0.7761507 -26.482951 -43.11828 0.003858942
[3997,] 0.8308660 0.7924643 -19.699762 -38.43458 0.003920541
[3998,] 0.8007775 0.8002707 -13.141932 -33.37605 0.003916109
[3999,] 0.7852284 0.8056239 -6.569699 -28.01478 0.003999789
[4000,] 0.8550499 0.8136852 2.197810 -21.97226 0.004293766
Сырые входные данные у нас готовы.
3.3.3. Выходные данные (целевая)
Перейдем к формированию выходных (целевых данных). Как мы выше говорили, будем применять ZigZag.
Возьмем ZigZag с шириной канала 37 больших пунктов. ZigZag будем вычислять по средней цене. Можно вычислять индикатор и по ценам HL, но по средней он менее "дерганный". Затем извлечем сигнал (0 - Buy, 1 -Sell) и конвертируем его в выходную матрицу, которую принимает модель сети.
Напишем функцию:
Out<-function(ch=0.0037){
# ЗигЗаг имеет значения (определен) на каждом баре а не только в вершинах
zz<-ZigZag(price[ ,'Med'], change = ch, percent = F, retrace = F, lastExtreme = T);
n<-1:length(zz);
# На последних барах неопределенные значения заменим на последние известные
for(i in n) { if(is.na(zz[i])) zz[i] = zz[i-1];}
#Определим скорость изменения ЗигЗага и сдвинем на один бар в будущее
dz<-c(diff(zz), NA);
#Если скорость >0 - сигнал = 0(Buy), если <0, сигнал = 1 (Sell) иначе NA
sig<-ifelse(dz>0, 0, ifelse(dz<0, 1, NA));
return(sig);
}
Вычислим сигналы.
> Y<-Out()
> table(Y)
Y
0 1
1567 2423
Соотношение классов разбалансировано. Количество примеров одного класса гораздо больше количества примеров другого. Все модели классификации относятся к таким наборам недружелюбно.
При разделении на тренировочную и тестовую выборки мы примем меры к исправлению этой ситуации.
3.3.4. Очистка данных
Очистим наши наборы от неопределенных данных. Под очисткой, в общем случае, понимают гораздо более широкий круг задач. Это и удаление "практически нулевых переменных" и удаление сильно коррелированых и некоторые другие задачи, которые мы в нашем случае применять не будем.
Напишем функцию и очистим наши данные
Clearing<-function(x, y){
dt<-cbind(x,y);
n<-ncol(dt)
dt<-na.omit(dt)
return(dt);
}
> dt<-Clearing(X,Y); nrow(dt)
[1] 3957
Матрица стала на 43 бара короче.
3.3.5. Формирование обучающей и тестовой выборок
Существует несколько способов разбиения исходных данных на обучающую и тестовую выборки. Мы применим обычное случайное разделение исходных данных на train и test в соотношении 8/10. Не забываем, что выборки должны быть стратифицированы, т.е. соотношение количества примеров классов в train и test должно соответствовать соотношению классов в исходном наборе. Кроме того, неплохо бы исправить неравенство классов в исходном наборе. Это можно сделать двумя способами — выровнять либо к большему, либо к меньшему классу. Поскольку нам желательно иметь больше примеров, выровняем к большему классу "1". Нам понадобится пакет "caret".
Сформируем новый сбалансированный набор, в котором количества примеров обоих классов будут одинаковы и будут равны большему.
3.3.6. Балансировка классов
Напишем функцию, которая выровняет количество классов в выборке в большую сторону (если расхождение больше 15%) и вернет сбалансированную матрицу
Balancing<-function(DT){
#Вычисляем таблицу с количеством классов
cl<-table(DT[ ,ncol(DT)]);
#Если разбаланс меньше 15%, возвращаем исходную матрицу
if(max(cl)/min(cl)<= 1.15) return(DT)
#Иначе балансируем в большую сторону
DT<-if(max(cl)/min(cl)> 1.15){
upSample(x = DT[ ,-ncol(DT)],y = as.factor(DT[ , ncol(DT)]), yname = "Y")
}
#Преобразуем у (фактор) в число
DT$Y<-as.numeric(DT$Y)
#Перекодируем у из 1,2 в 0,1
DT$Y<-ifelse(DT$Y == 1, 0, 1)
#Преобразуем датафрейм в матрицу
DT<-as.matrix(DT)
return(DT);
}
Краткое пояснение. В первой строке вычисляем количество примеров каждого класса (вектор, размерность которого равна количеству классов).
Находим отношение большего к меньшему, и если оно меньше установленного порога, выходим. Если больше, вычисляем функцию, подав раздельно х и y, который предварительно преобразуем в фактор.
Таково требование к формальным параметрам функции upSample(). Поскольку целевая в качестве фактора нам не нужна, мы ее преобразуем обратно в числовую со значениями 0 и 1. Обратите внимание! При преобразовании числовой (0,1) в фактор мы получаем текстовые "0" и "1". При обратном преобразовании в числовые мы получим 1 и 2 (!). Их мы заменяем на 0 и 1. Последней строкой мы преобразуем наш набор из класса "датафрейм" в класс "матрица". Вычислим ее:
dt.b<-Balancing(dt)
x<-dt.b[ ,-ncol(dt.b)]
y<-dt.b[ , ncol(dt.b)]
Таким образом у нас готов исходный dt набор данных (входных и выходных) и сбалансированный dt.b набор.
Разделим на train/test выборки
С помощью функции holdout() из пакета "rminer" получим индексы тренировочной и тестовой выборок
> library('rminer')
> t<-holdout(y, ratio = 8/10, mode = "random")
Объект t - лист содержащий индексы тренировочного (t$tr) и тестового наборов (t$ts). Выдаваемые наборы стратифицированы.
3.3.7. Препроцессинг
В нашем наборе входных данных находятся переменные с самыми различными диапазонами величин. Нужно вспомнить, что глубокие сети, по сути, просто нейросети с особенным способом инициализации весов.
Нейросети на вход могут принимать переменные в диапазоне (-1; 1) или (0, 1). Нормализуем входные переменные в диапазон [-1, 1].
Воспользуемся функцией preProcess() из пакета "caret". Обратить внимание, что параметры препроцессинга нужно вычислять на тренировочном наборе и сохранить их для дальнейшего препроцессинга тестового набора и вновь поступивших данных.
> spSign<-preProcess(x[t$tr, ], method = "spatialSign")
> x.tr<-predict(spSign, x[t$tr, ])
> x.ts<-predict(spSign, x[t$ts, ])
У нас все готово для построения, обучения и тестирования модели глубокой сети.
3.4. Построение, обучение и тестирование моделей
Построим и обучим модель DN SAE. Формула модели и описание переменных:
sae.dnn.train(x, y, hidden = c(10), activationfun = "sigm", learningrate = 0.8, momentum = 0.5, learningrate_scale = 1, output = "sigm", sae_output = "linear",
numepochs = 3, batchsize = 100, hidden_dropout = 0, visible_dropout = 0)
где:
- х - матрица входных данных;
- y - вектор или матрица целевых переменных;
- hidden - вектор с числом нейронов в каждом скрытом слое. По умолчанию с(10);
- activationfun - функция активации скрытых нейронов. Может быть "sigm", "linear", "tanh". По умолчанию "sigm";
- learningrate - уровень обучения для градиентного спуска. По умолчанию = 0.8;
- momentum - момент для градиентного спуска. По умолчанию = 0.5;
- learningrate_scale - уровень обучения может быть умножен на эту величину после каждой итерации. По умолчанию =1.0;
- numepochs - количество итераций для обучения. По умолчанию =3;
- batchsize - размер мини порций на которых проводится обучение. По умолчанию =100;
- output - функция активации для выходных нейронов, может быть "sigm", "linear", "softmax". По умолчанию "sigm";
- sae_output - функция активации выходных нейронов SAE, может быть "sigm", "linear", "softmax". По умолчанию "linear";
- hidden_dropout - удаляемая часть для скрытых слоев. По умолчанию =0;
- visible_dropout - удаляемая часть видимого (входного) слоя. По умолчанию =0.
Создадим модель размером (17, 100, 100, 100, 1), обучим ее, замерив время обучения, и посмотрим метрики предсказаний.
> system.time(SAE<-sae.dnn.train(x= x.tr, y= y[t$tr], hidden=c(100,100,100), activationfun = "tanh", learningrate = 0.6, momentum = 0.5, learningrate_scale = 1.0, output = "sigm", sae_output = "linear", numepochs = 10, batchsize = 100, hidden_dropout = 0, visible_dropout = 0))
begin to train sae ......
training layer 1 autoencoder ...
training layer 2 autoencoder ...
training layer 3 autoencoder ...
sae has been trained.
begin to train deep nn ......
deep nn has been trained.
user system elapsed
12.92 0.00 13.09
Как видим, обучение происходит в два этапа. Сначала послойно тренируются AE, после чего собственно тренируется нейросеть.
Умышленно установлено небольшое количество эпох обучения и огромное количество скрытых нейронов в трех слоях. Весь процесс занял чуть больше 13 сек!
Посмотрим на предсказания по тестовому набору предикторов.
> pr.sae<-nn.predict(SAE, x.ts);
> summary(pr.sae)
V1
Min. :0.2649
1st Qu.:0.2649
Median :0.5881
Mean :0.5116
3rd Qu.:0.7410
Max. :0.7410
Преобразуем в уровни 0,1 и вычислим метрики
> pr<-ifelse(pr.sae>mean(pr.sae), 1, 0)
> confusionMatrix(y[t$ts], pr)
Confusion Matrix and Statistics
Reference
Prediction 0 1
0 316 128
1 134 378
Accuracy : 0.7259
95% CI : (0.6965, 0.754)
No Information Rate : 0.5293
P-Value [Acc > NIR] : <2e-16
Kappa : 0.4496
Mcnemar's Test P-Value : 0.7574
Sensitivity : 0.7022
Specificity : 0.7470
Pos Pred Value : 0.7117
Neg Pred Value : 0.7383
Prevalence : 0.4707
Detection Rate : 0.3305
Detection Prevalence : 0.4644
Balanced Accuracy : 0.7246
'Positive' Class : 0
Коэффициент не выдающийся. Но нам важен не коэффициент а прибыль, которую мы получим по этим сигналам. Проверим это на последних 500 барах (приблизительно неделя).
Получим сигналы на последовательных последних 500 барах от нашей обученной сети.
Нормализуем последние 500 входных данных, получим предсказания от обученной нейросети и конвертируем их в сигналы -1= (Sell) и 1 = (Buy)
> new.x<-predict(spSign,tail(dt[ ,-ncol(dt)], 500))
> pr.sae1<-nn.predict(SAE, new.x)
> pr.sig<-ifelse(pr.sae1>mean(pr.sae1), -1, 1)
> table(pr.sig)
pr.sig
-1 1
235 265
> new.y<-ifelse(tail(dt[ , ncol(dt)], 500) == 0, 1, -1)
> table(new.y)
new.y
-1 1
201 299
> cm1<-confusionMatrix(new.y, pr.sig)
> cm1
Confusion Matrix and Statistics
Reference
Prediction -1 1
-1 160 41
1 75 224
Accuracy : 0.768
95% CI : (0.7285, 0.8043)
No Information Rate : 0.53
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.5305
Mcnemar's Test P-Value : 0.002184
Sensitivity : 0.6809
Specificity : 0.8453
Pos Pred Value : 0.7960
Neg Pred Value : 0.7492
Prevalence : 0.4700
Detection Rate : 0.3200
Detection Prevalence : 0.4020
Balanced Accuracy : 0.7631
'Positive' Class : -1
Коэффициент Accuracy неплох! Но опять же, нас интересует не коэффициент, а прибыль.
Протестируем с нашими предсказанными сигналами прибыль на последних 500 барах и получим кривую баланса:
> bal<-cumsum(tail(price[ , 'CO'], 500) * pr.sig)
> plot(bal, t = "l")
> abline(h = 0)
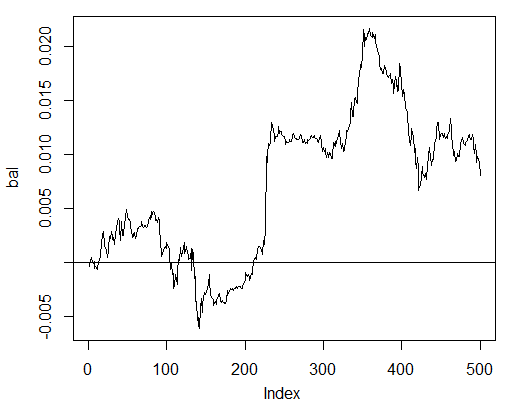
Рис. 24. Баланс на последних 500 барах по сигналам нейросети
Баланс посчитан без учета спрэда, проскальзывания и прочих прелестей реального рынка.
Сравним с балансом, который бы получился по идеальным сигналам от ZZ. Красная линия - баланс по сигналам нейросети:
> bal.zz<-cumsum(tail(price[ , 'CO'], 500) * new.y)
> plot(bal.zz, t = "l")
> lines(bal, col = 2)
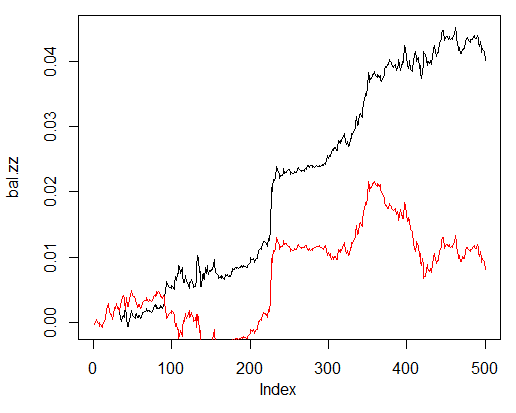
Рис. 25. Баланс на последних 500 барах по сигналам нейросети и сигналам ZigZag
Есть потенциал для улучшения.
Для облегчения тестирования напишем две вспомогательные функции Estimation() и Testing(). Первая будет выдавать коэффициенты (Accuracy/Err) а вторая баланс (Bal/BalZZ).
Это позволит (меняя некоторые
параметры сети) сразу получать результат, и увидеть, какие параметры и как влияют на качество полученной сети.
В последующем, написав фитнес функцию, можно будет найти оптимальные параметры сети с помощью эволюционных (генетических) алгоритмов, не прерывая процесс торговли. В этой статье мы этим заниматься не будем, может быть, сделаем это в следующей.
Итак, функция Estimation(), вычисляющая коэффициенты (Err/Accuracy):
Estimation<-function(X, Y, r = 8/10, m = "random", norm = "spatialSign",
h = c(10), act = "tanh", LR = 0.8, Mom = 0.5,
out = "sigm", sae = "linear", Ep = 10, Bs = 50,
CM=F){
#Индексы тренировочного и тестового наборов
t<-holdout(Y, ratio = r, mode = m)
#Параметры препроцессинга
prepr<-preProcess(X[t$tr, ], method = norm)
#Разделяем на train и test наборы с препроцессингом
x.tr<-predict(prepr, X[t$tr, ])
x.ts<-predict(prepr, X[t$ts, ])
y.tr<- Y[t$tr]; y.ts<- Y[t$ts]
#Обучаем модель
SAE<-sae.dnn.train(x = x.tr , y = y.tr , hidden = h,
activationfun = act,
learningrate = LR, momentum = Mom,
output = out, sae_output = sae,
numepochs = Ep, batchsize = Bs)
#Получаем предсказание по тестовому набору
pr.sae<-nn.predict(SAE, x.ts)
#Перекодируем его в сигналы 1,0
pr<-ifelse(pr.sae>mean(pr.sae), 1, 0)
#Вычисляем коэффициент Accuracy или ошибку классификации
if(CM) err<-unname(confusionMatrix(y.ts, pr)$overall[1])
if(!CM) err<-nn.test(SAE, x.ts, y.ts, mean(pr.sae))
return(err)
}
Формальные параметры:
- X – матрица входных сырых предикторов;
- Y – вектор целевой переменной;
- r – соотношение train/test;
- m – режим формирования выборок (случайный или последовательный);
- norm – режим нормирования входных переменных ([ -1, 1]= "spatialSign";[0, 1]="range");
- h – вектор с количеством нейронов в скрытых слоях;
- act – функция активации скрытых нейронов;
- LR – уровень обучения;
- Мом — момент;
- out – функция активации выходного слоя;
- sae – функция активации автоэнкодера;
- Ep – количество эпох обучения;
- Bs – размер мини выборок;
- СM– булева , если TRUE выводится Accuracy. иначе Err.
Например, вычислим ошибку классификации на несбалансированном наборе dt сетью с тремя скрытыми слоями по 30 нейронов в каждом:
> Err<-Estimation(X = dt[ ,-ncol(dt)], Y = dt[ ,ncol(dt)], h=c(30, 30, 30), LR= 0.7)
begin to train sae ......
training layer 1 autoencoder ...
training layer 2 autoencoder ...
training layer 3 autoencoder ...
sae has been trained.
begin to train deep nn ......
deep nn has been trained.
> Err
[1] 0.1376263
Следующая функция Testing() вычисляет баланс по прогнозным сигналам или по идеальным (ZigZag):
Testing<-function(dt1, dt2, r=8/10, m = "random", norm = "spatialSign",
h = c(10), act = "tanh", LR = 0.8, Mom = 0.5,
out = "sigm", sae = "linear", Ep = 10, Bs=50,
pr = T, bar = 500){
X<-dt1[ ,-ncol(dt1)]
Y<-dt1[ ,ncol(dt1)]
t<-holdout(Y, ratio = r, mode = m)
prepr<-preProcess(X[t$tr, ], method = norm)
x.tr<-predict(prepr, X[t$tr, ])
y.tr<- Y[t$tr];
SAE<-sae.dnn.train(x = x.tr , y = y.tr , hidden = h,
activationfun = act,
learningrate = LR, momentum = Mom,
output = out, sae_output = sae,
numepochs = Ep, batchsize = Bs)
X<-dt2[ ,-ncol(dt2)]
Y<-dt2[ ,ncol(dt2)]
x.ts<-predict(prepr, tail(X, bar))
y.ts<-tail(Y, bar)
pr.sae<-nn.predict(SAE, x.ts)
sig<-ifelse(pr.sae>mean(pr.sae), -1, 1)
sig.zz<-ifelse(y.ts == 0, 1,-1 )
bal<-cumsum(tail(price[ ,'CO'], bar) * sig)
bal.zz<-cumsum(tail(price[ ,'CO'], bar) * sig.zz)
if(pr) return(bal)
if(!pr) return(bal.zz)
}
Формальные параметры:
- dt1 – матрица входных и целевой, на которой проводится обучение сети;
- dt2 - матрица входных и целевой, на которой проводится тестирование обученной сети;
- pr – булева, если TRUE выводим баланс по предсказанным сигналам, иначе по ZigZag;
- bar -на скольких последних барах считать баланс.
Например, подсчитаем баланс на последних 500 барах нашего набора dt при обучении на сбалансированном наборе dt.b нейросетью с такими же параметрами, как выше:
> Bal<-Testing(dt.b, dt, h=c(30, 30, 30), LR= 0.7)
begin to train sae ......
training layer 1 autoencoder ...
training layer 2 autoencoder ...
training layer 3 autoencoder ...
sae has been trained.
begin to train deep nn ......
deep nn has been trained.
> plot(Bal, t = "l")
> abline(h = 0)
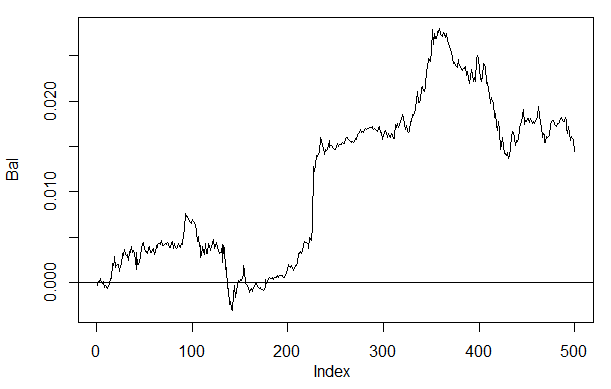
Рис. 26. Баланс на последних 500 барах по сигналам нейросети h(30,30,30)
Если сравним с ранее полученным балансом, то увидим значительные улучшения. Интересно другое.
Если посмотреть на график цены на этих последних 500 барах, то мы увидим, какие участки больше всего понравились нашей нейросети (150-350 бары).
> plot(tail(price[ ,'Close'], 500), t = "l")
> abline(v = c(150,350), col=2)
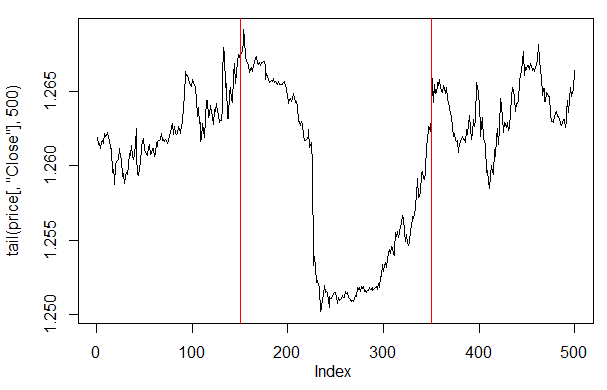
Рис. 27. График цены Close на последних 500 барах
Замечание: При декодировании предсказанных выходов мы приняли упрощенный вариант больше/меньше средней. Но применяются и другие варианты.
Например, больше 0.6 или меньше 0.4 (вырезается нестабильный участок 0.4-0.6). Еще более точные границы классов можно получить при калибровке. Об этом позже.
Изменим немного нашу функцию Testing(), введя дополнительный параметр dec, который позволяет выбрать вариант декодирования ("mean" или "60/40") и проверим на тех же предсказанных значениях, как это повлияет на баланс.
Testing.1<-function(dt1, dt2, r = 8/10, m = "random", norm = "spatialSign",
h = c(10), act = "tanh", LR = 0.8, Mom = 0.5,
out = "sigm", sae = "linear", Ep = 10, Bs = 50,
pr = T, bar = 500, dec=1){
X<-dt1[ ,-ncol(dt1)]
Y<-dt1[ ,ncol(dt1)]
t<-holdout(Y, ratio = r, mode = m)
prepr<-preProcess(X[t$tr, ], method = norm)
x.tr<-predict(prepr, X[t$tr, ])
y.tr<- Y[t$tr];
SAE<-sae.dnn.train(x = x.tr , y = y.tr , hidden = h,
activationfun = act,
learningrate = LR, momentum = Mom,
output = out, sae_output = sae,
numepochs = Ep, batchsize = Bs)
X<-dt2[ ,-ncol(dt2)]
Y<-dt2[ ,ncol(dt2)]
x.ts<-predict(prepr, tail(X, bar))
y.ts<-tail(Y, bar)
pr.sae<-nn.predict(SAE, x.ts)
#Вариант +/- mean
if(dec == 1) sig<-ifelse(pr.sae>mean(pr.sae), -1, 1)
#Вариант 60/40
if(dec == 2) sig<-ifelse(pr.sae>0.6, -1, ifelse(pr.sae<0.4, 1, 0))
sig.zz<-ifelse(y.ts == 0, 1,-1 )
bal<-cumsum(tail(price[ ,'CO'], bar) * sig)
bal.zz<-cumsum(tail(price[ ,'CO'], bar) * sig.zz)
if(pr) return(bal)
if(!pr) return(bal.zz)
}
Посчитаем и посмотрим баланс с первым и вторым вариантом декодирования.
Для повторяемости результатов перед каждым запуском функции установим ГСЧ в одинаковое значение.
> set.seed<-1245
> Bal1<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 1)
begin to train sae ......
training layer 1 autoencoder ...
training layer 2 autoencoder ...
training layer 3 autoencoder ...
sae has been trained.
begin to train deep nn ......
deep nn has been trained.
> set.seed<-1245
> Bal2<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 2)
begin to train sae ......
training layer 1 autoencoder ...
training layer 2 autoencoder ...
training layer 3 autoencoder ...
sae has been trained.
begin to train deep nn ......
deep nn has been trained.
> plot(Bal2, t = "l")
> lines(Bal1, col = 2)
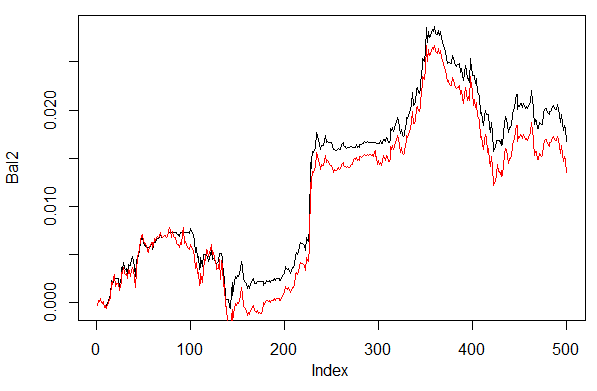
Рис. 28. Баланс на последних 500 барах по сигналам нейросети с различными способами декодирования предсказаний
Как видим, баланс по второму варианту 60/40 выглядит лучше. Так что и в этом направлении есть смысл искать пути улучшения результатов.
Ну и последнее. Теория говорит, что ансамбль из нескольких нейросетей дает лучший и более стабильный результат. Проверим на ансамбле из нескольких нейросетей, которые будут обучаться на одинаковых выборках (хотя ничто не мешает обучить их на независимых выборках). Результат предсказания ансамбля определим как простое среднее из предсказаний всех сетей. Существуют и другие, более изощренные способы усреднения.
Доработаем нашу функцию Testing(), добавив в нее еще один параметр — ans=1 , указывающий количество сетей в ансамбле.
3.4.1. Параллельные вычисления
Учитывая, что вычисления по нескольким независимым моделям хорошо распараллеливаются, используем возможность, предоставляемую языком R и для вычисления создадим кластер из нескольких ядер нашего процессора или компьютеров локальной сети (если у вас несколько компьютеров), независимо от того, с какой ОС эти компьютеры.
Для этого нам понадобится чудесный пакет "foreach" и пакет "doParallel". Напишем простенькую функцию, которая будет запускать кластер на всех ядрах нашего процессора.
library(doParallel)
library(foreach)
puskCluster<-function(){
cores<-detectCores()
cl<-makePSOCKcluster(cores)
registerDoParallel(cl)
clusterSetRNGStream(cl)
return(cl)
}
Несколько пояснений. В первых двух строчках мы загружаем необходимые библиотеки (они должны быть предварительно инсталлированы на вашем компьютере). Дальше определяем, сколько ядер имеет процессор, создаем
кластер, регистрируем пакет для параллельных вычислений, устанавливаем в каждый поток вычислений независимый генератор случайных чисел (ГСЧ) и возвращаем хендл кластера. Вообще, тема качества ГСЧ в вычислениях различных моделей чрезвычайно важна. Но это отдельная тема.
Итак, после того как мы запустили кластер и произвели необходимые вычисления, не забываем его остановить:
cl<-puskCluster()
stopCluster(cl)
Параллельные вычисления будем производить по следующей формуле из пакета "foreach":
SAE<-foreach(times(ans), .packages = "deepnet") %dopar%
sae.dnn.train(x = x.tr , y = y.tr , hidden = h,
activationfun = act,
learningrate = LR, momentum = Mom,
output = out, sae_output = sae,
numepochs = Ep, batchsize = Bs)
где times(ans) - количество сетей, которые мы хотим получить, а .packages указывает из какого пакета брать вычисляемую функцию.
Результат в виде листа будет содержать необходимое нам количество обученных сетей.
Дальше нам нужно получить предсказания от каждой нейросети, и вычислить среднее.
pr.sae<-(foreach(i = 1:ans, .combine = "+") %do% nn.predict(SAE[[i]], x.ts))/ans
Несколько пояснений, i – вектор индексов обученных нейросетей,.combine="+" указывает в каком виде вернуть вычисленные предикты по всем нейросетям. В нашем случае мы попросили вернуть сумму и выполняем мы эти вычисления последовательно, не параллельно (оператор %do%). После этого мы разделили эту сумму на количество нейросетей и получим окончательный результат. Просто и элегантно.
Вычислим баланс, полученный с использованием ансамбля из 3 и 4 нейросетей с теми же параметрами, что и в предыдущих расчетах и декодированием 60/40. Сравним с результатами на одной нейросети. Для определения эффективности параллельных вычислений увеличим количество эпох до 300, и замерим время выполнения прогноза.
1. Одна нейросеть:
> system.time(Bal21<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 2, Ep=300))
begin to train sae ......
training layer 1 autoencoder ...
####loss on step 10000 is : 0.000057
####loss on step 20000 is : 0.000043
training layer 2 autoencoder ...
####loss on step 10000 is : 0.000081
####loss on step 20000 is : 0.000086
training layer 3 autoencoder ...
####loss on step 10000 is : 0.000072
####loss on step 20000 is : 0.000066
sae has been trained.
begin to train deep nn ......
####loss on step 10000 is : 0.069451
####loss on step 20000 is : 0.079629
deep nn has been trained.
user system elapsed
115.78 0.00 116.96
> plot(Bal21, t = "l")
> abline(h = 0)
2. Ансамбль из 3 нейросетей:
> system.time(Bal41<-Testing.2(dt.b, dt, h = c(30, 30, 30), LR = 0.7, Ep=300, dec = 2, ans=3))
user system elapsed
0.22 0.06 233.64
> lines(Bal41, col=4)
3. Ансамбль из 4 нейросетей:
> system.time(Bal44<-Testing.2(dt.b, dt, h = c(30, 30, 30), LR = 0.7, Ep=300, dec = 2, ans=4))
user system elapsed
0.13 0.03 247.86
> lines(Bal44, col=2)
Как видим, время выполнения при параллельном вычислении оптимально, если количество потоков кратно количеству ядер. У меня задействовано 2 ядра.
А вот преимущества в балансе практически нет. На графике внизу синий - 3 сети, красный - 4 сетки, черный - одна сетка.
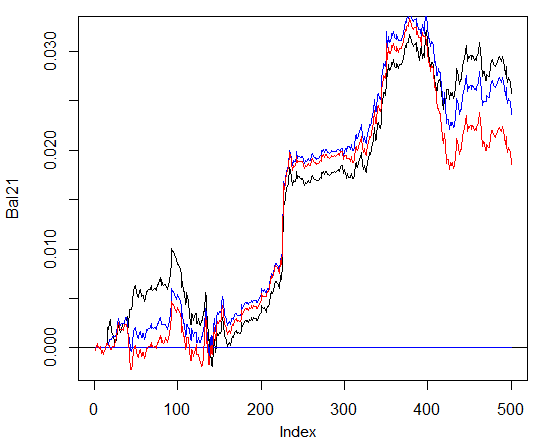
Рис. 29. Баланс на последних 500 барах по сигналам ансамблей, состоящих из 3 и 4 нейросетей и одной нейросети
В общем случае результат зависит от очень многих параметров, начиная с входных и выходных данных, способа их нормирования, количества скрытых слоев и количества нейронов в этих слоях, уровня обучения,
количества эпох обучения и многих, многих других.
Последние три примера. Посчитаем баланс на последних 1000 барах тремя нейросетями с различным количеством скрытых нейронов в трех скрытых слоях.
> system.time(Bal0<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 2, Ep=300, bar=1000))
begin to train sae ......
training layer 1 autoencoder ...
####loss on step 10000 is : 0.000054
####loss on step 20000 is : 0.000044
training layer 2 autoencoder ...
####loss on step 10000 is : 0.000078
####loss on step 20000 is : 0.000079
training layer 3 autoencoder ...
####loss on step 10000 is : 0.000090
####loss on step 20000 is : 0.000072
sae has been trained.
begin to train deep nn ......
####loss on step 10000 is : 0.072633
####loss on step 20000 is : 0.057917
deep nn has been trained.
user system elapsed
116.09 0.02 116.26
> max(Bal0)
[1] 0.04725
> plot(Bal0, t="l")
> tail(Bal0,1)
[1] 0.03514
Максимальный профит 472 пункта, на последнем баре 351 п. На графике отражен черным цветом.
> system.time(Bal0<-Testing.1(dt.b, dt, h = c(13, 8, 5), LR = 0.7, dec = 2, Ep=300, bar=1000))
begin to train sae ......
training layer 1 autoencoder ...
####loss on step 10000 is : 0.005217
####loss on step 20000 is : 0.004846
training layer 2 autoencoder ...
####loss on step 10000 is : 0.051324
####loss on step 20000 is : 0.046230
training layer 3 autoencoder ...
####loss on step 10000 is : 0.023292
####loss on step 20000 is : 0.026113
sae has been trained.
begin to train deep nn ......
####loss on step 10000 is : 0.057788
####loss on step 20000 is : 0.056932
deep nn has been trained.
user system elapsed
64.04 0.01 64.24
Warning message:
In sae$encoder[[i - 1]]$W[[1]] %*% t(train_x) + sae$encoder[[i - :
longer object length is not a multiple of shorter object length
> lines(Bal0, col="blue")
Явно слабый вариант.
И третий вариант:
> system.time(Bal0<-Testing.1(dt.b, dt, h = c(50, 50, 50), LR = 0.7, dec = 2, Ep=300, bar=1000))
begin to train sae ......
training layer 1 autoencoder ...
####loss on step 10000 is : 0.000018
####loss on step 20000 is : 0.000013
training layer 2 autoencoder ...
####loss on step 10000 is : 0.000062
####loss on step 20000 is : 0.000048
training layer 3 autoencoder ...
####loss on step 10000 is : 0.000053
####loss on step 20000 is : 0.000055
sae has been trained.
begin to train deep nn ......
####loss on step 10000 is : 0.096490
####loss on step 20000 is : 0.084860
deep nn has been trained.
user system elapsed
186.18 0.00 186.39
> lines(Bal0, col="red")
> max(Bal0)
[1] 0.0543
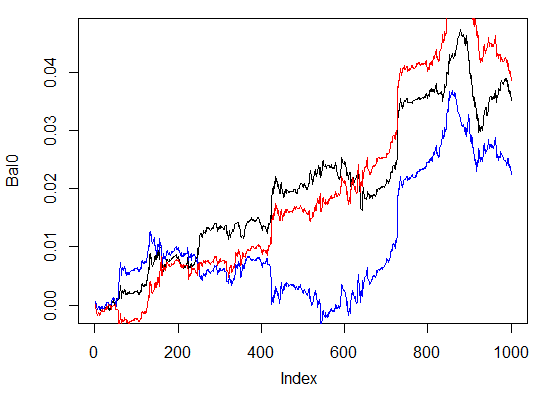
Рис. 30. Баланс на последних 1000 барах по сигналам трех нейросетей с различным количеством скрытых нейронов
Как видим, последний вариант лучший из трех, максимальный профит 543 пункта(!). И это мы изменили (от потолка) только количество скрытых нейронов, и уже есть значительное улучшение. Поэтому поиск оптимальных
параметров нужно производить с помощью эволюционных алгоритмов. Эти исследования для самостоятельной работы.
Кроме того, не забываем, что в этом пакете не полностью реализован авторский алгоритм.
4. Программная реализация (индикатор и эксперт)
Перейдем к программной реализации индикатора и эксперта, использующих глубокую сеть для получения торговых сигналов.
Возможна реализация в двух вариантах:
- Первый. Всю работу по обучению нейросети проводим в Rstudio врукопашную. После получения приемлемых результатов сохраняем нейросеть в соответствующем каталоге. Затем запускаем эксперт и
индикатор на графике. Эксперт загружает обученную сеть. Индикатор на каждом новом баре готовит вектор новых входных данных и передает их эксперту. Эксперт предъявляет данные нейросети, получает сигнал и далее его выполняет. Эксперт занимается своими обычными обязанностями (открыть, закрыть, тралить, ММ и т.п.). Задача индикатора подготовить и передать эксперту новые входные данные на каждом новом баре и, что более важно, выводить на график сигналы, полученные от нейросети при предсказании. Визуальный контроль, как показала практика, наиболее эффективный способ оценки работы нейросети.
- Второй. Запускаем на графике эксперт и индикатор. При первом запуске индикатор передает эксперту подготовленный большой набор входных и выходных данных. Эксперт запускает обучение, тестирование и
выбор лучшей нейросети. После этого работа продолжается по первому варианту.
Мы построим связку индикатор-эксперт по первому варианту. Эксперт с минимумом "рюшечек".
Предваряя вопрос — почему так сложно? Такой вариант исполнения дает возможность подключать к одному эксперту несколько индикаторов, расположенных на разных символах/таймфреймах, и, соответственно, работать на них. Для этого нужно будет сделать небольшую модернизацию эксперта. Но об этом позже.
Ниже представлена схема взаимодействия индикатора и эксперта:
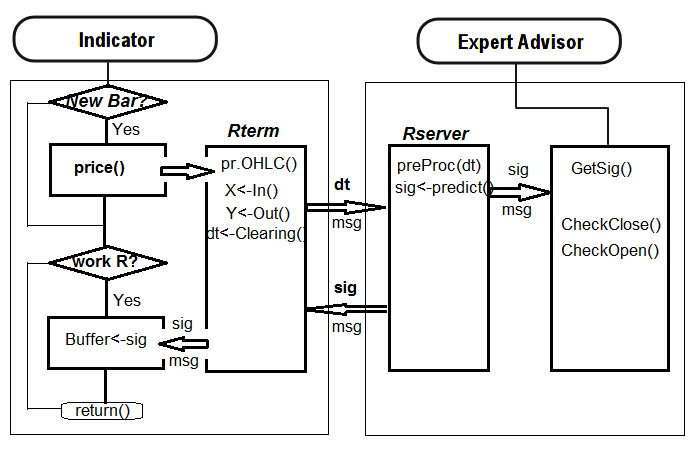
Рис. 31. Структурная схема взаимодействия индикатора и эксперта
4.1. Обучение и сохранение модели
С помощью индикатора, установленного на нужном нам графике, получим все необходимые исходные данные. Для этого нужно бросить индикатор на график, установив входную переменную send=false, т.е. - "картинку" писать, на сервер не отправлять. При первом запуске на этом символе или таймфрейме индикатор создаст в папке данных терминала (/MQL4/Files) следующие директории: /Symbol/TF/Test_Data/.
Такая организация директорий дает возможность не сваливать в одну кучу результаты экспериментов при предварительном обучении моделей и не затирать старые данные новыми. В директории /Symbol/TF/Test_Data/ будут находиться все ваши промежуточные результаты ежедневного труда, а в директории /Symbol/TF/ будет располагаться модель, по которой будет работать эксперт (туда ее нужно будет перенести вручную). Такой же результат будет получен при первом запуске на новом символе или таймфрейме эксперта.
Итак. На символе EURUSD ТФ(М30) 4000 баров по состоянию на 14.10.14. Нам нужен датафрейм dt[].
Сбалансируем классы:
> dt.b<-Balancing(dt)
> table(dt.b[ ,ncol(dt.b)])
0 1
2288 2288
Теперь с помощью ранее написанной функции Testing.1() обучим глубокую нейросеть количеством эпох (500 и 300) и посмотрим баланс, полученный на последних 500 барах по предсказанным нейросетью сигналам.
> system.time(bal<-Testing.1(dt.b, dt, h = c(50, 50, 50), LR = 0.7, dec = 2, Ep=500, bar=500))
begin to train sae ......
training layer 1 autoencoder ...
####loss on step 10000 is : 0.000017
####loss on step 20000 is : 0.000015
####loss on step 30000 is : 0.000015
training layer 2 autoencoder ...
####loss on step 10000 is : 0.000044
####loss on step 20000 is : 0.000041
####loss on step 30000 is : 0.000039
training layer 3 autoencoder ...
####loss on step 10000 is : 0.000042
####loss on step 20000 is : 0.000042
####loss on step 30000 is : 0.000036
sae has been trained.
begin to train deep nn ......
####loss on step 10000 is : 0.089417
####loss on step 20000 is : 0.043276
####loss on step 30000 is : 0.069399
deep nn has been trained.
user system elapsed
267.59 0.08 269.37
> plot(bal, t="l")
Сохраним нейросеть под другим именем и обучим вторую
> SAE1<-SAE
> system.time(bal<-Testing.1(dt.b, dt, h = c(50, 50, 50), LR = 0.7, dec = 2, Ep=300, bar=500))
begin to train sae ......
training layer 1 autoencoder ...
####loss on step 10000 is : 0.000020
####loss on step 20000 is : 0.000016
training layer 2 autoencoder ...
####loss on step 10000 is : 0.000050
####loss on step 20000 is : 0.000050
training layer 3 autoencoder ...
####loss on step 10000 is : 0.000051
####loss on step 20000 is : 0.000043
sae has been trained.
begin to train deep nn ......
####loss on step 10000 is : 0.083888
####loss on step 20000 is : 0.083941
deep nn has been trained.
user system elapsed
155.32 0.02 156.25
> lines(bal, col=2)
Посмотрим на графики баланса (красным последний результат).
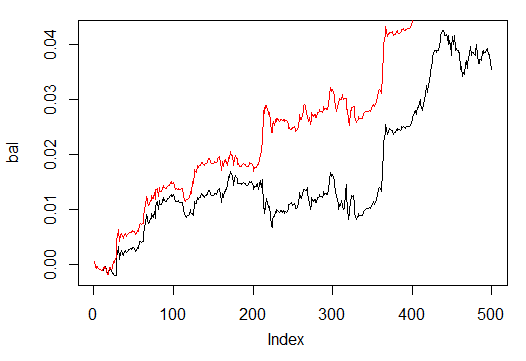
Рис. 32. Баланс на последних 500 барах по сигналам нейросетей обученых количеством эпох 500 и 300
Как видим, нейросеть, обученная в течение 300 эпох, показала результат лучше, чем сеть с 500.
Время обучения последней сети вполне приемлемо для оперативного переобучения во время торговли на этом таймфрейме.
Для дальнейшей работы на реальном графике нам нужны два объекта: обученная модель "SAE" и параметры нормализации входных данных - "prepr". Сохраним их в соответствующей директории, у меня это "D:/Alpari
Limited MT4/MQL4/Files/EURUSD/M30/Test_2014-10-14" (она уже определена и установлена как рабочая, если вы открыли сохраненную индикатором рабочую область "i_SAE_EURUSD_30.Rdata" в Rstudio.
save(SAE, prepr, file="SAE.model")
В файле "SAE.model" мы сохранили собственно модель и параметры нормализации, без которых применение модели бессмысленно. Вы можете экспериментировать и сохранять понравившиеся вам модели каждый день, они будут складываться в папки "/File/Symbol/TF/Test_Data". Для использования модели экспертом файл "SAE.model" нужно переложить в папку "File/Symbol/TF/" вручную и в этой папке может быть только одна модель, по которой и будет работать эксперт.
Теперь загрузив файл (load("SAE.model")) эксперт загрузит в рабочую область эти объекты для использования в работе. На этом ручная часть работы закончена, можно ставить индикатор-эксперт на график и тестировать в реальном времени.
Для определения эффективности работы эксперта нужны количественные критерии. Как показывает опыт, коэффициент Accuracy не очень подходит на эту роль.
Можно использовать среднее от отношения баланса по предсказаниям к балансу по ZigZag или отношение баланса на последнем баре к количеству баров. Например, в нашем случае баланс по ZigZag:
sig.zz<-ifelse(tail(dt[ , ncol(dt)], 500) == 0, 1, -1)
bal.zz<-cumsum(tail(price[ , 'CO'], 500) * sig.zz)
Kzz<-mean(bal.zz / bal)
> Kzz
[1] 0.9173312
Это очень высокий показатель, но он относительный.
Если посмотреть, как он выглядит во времени, то можно увидеть, что на первых 50-100 барах это нестабильный показатель, хотя потом он становиться практически
постоянным. Статистики приведены ниже:
> plot(bal/bal.zz, t="l")
> summary(bal/bal.zz)
Min. 1st Qu. Median Mean 3rd Qu. Max.
-15.2500 0.7341 0.7844 0.9173 0.8833 55.0000
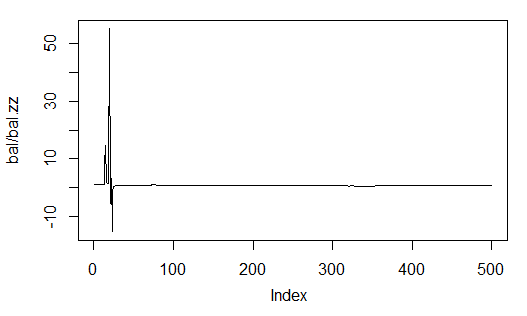
Рис. 33. Отношение баланса по предсказаниям к балансу по ZigZag
Второй более конкретный, он показывает, сколько пунктов прибыли приходится на один бар на отрезке длиной N баров.
Например, для баланса по предсказаниям нейросети на отрезке в 500 баров:
> Kb<-tail(bal,1)/length(bal)*10^Dig
> Kb
[1] 11.508
и
по сигналам Зигзага:
> Kbz<-tail(bal.zz,1)/length(bal)*10^Dig
> Kbz
[1] 13.784
Определив нижнюю границу эффективности по одному из этих показателей, мы можем знать момент, когда нужно переучить нейросеть или оптимизировать ее параметры.
Эксперт будет выводить на график следующие показатели OP – выполняемая операция, Acc – Accuracy, K – это Kb определенный выше, Kmax – это такой же показатель как Kb но определенный на пике баланса (дает представление насколько отличается этот показатель на последнем баре от максимального).
4.2. Порядок установки и запуска
В приложенном архиве SAE.zip находятся:
- Индикатор i_SAE.mq4, положить в папку ~/MQL4/Indicators/
- Эксперт e_SAE.mq4, положить в папку ~/MQL4/Experts/
- Библиотека mt4Rb7.dll, положить в папку ~/MQL4/Libraries/.
- Заголовочный файл mt4Rb7.mqh, положить в папку ~/MQL4/Include/. Библиотеку и заголовочный файл разработал и предоставил добрый человек Bernd Kreuss. В наименовании я добавил индекс последнего изменения (b7). При наличии многих версий (как у меня) с одинаковыми именами случаются казусы, которые отнимают море времени на их отлов.
- Скрипты на R: i_SAE.r (основной скрипт индикатора), i_SAE_fun.r (функции скрипта индикатора), e_SAE.r (скрипт эксперта), e_SAE_init.r(скрипт инициализации эксперта), SAE_SetDir.r (скрипт проверки и создания необходимых директорий). Поскольку скрипты не зависят ни от символа, ни от таймфрейма, ни от терминала, их можно расположить в отдельной директории (у меня "C:Rdata/SAE/"). В директории "C:Rdata/" находятся различные скрипты, не привязанные к конкретному проекту. Если вы положили скрипты в папку отличную от моей, внесите соответствующие изменения в индикатор и эксперт (поправьте путь к скриптам).
- SAE.model - файл с моделью "SAE" и параметрами нормализации - "prepr". Модель обучена на данных EURUSD (M30) последней датой 14.10.14. Процесс обучения в статье выше.
Также не забудьте поправить путь к директории, в которой находится инсталлированный язык R на вашем компьютере.
Запуск для работы желательно производить в следующей последовательности: устанавливаем на график эксперт. Если вы решили установить еще один эксперт на другом символе, нужно указать порт, отличный от ранее запущенных серверов, например port = 8886 (по умолчанию port = 8888).
Замечение. Это абсолютно нерациональный вариант. Каждый сервер занимает около 120-130 Mb. Но пока так.
После нормальной инициализации эксперта появится алерт "Нет результата вычислений! Symbol". После этого устанавливаете индикатор с внешней переменной send = true и с указанием порта сервера, к которому должен подключиться индикатор (см. выше). Если все работает нормально, в выводимой строке появятся реальные данные - "операция", Accuracy, K и Kmax и начнется торговля.
Контролировать состояние работы R-процесса лучше всего, открыв окно диспетчера задач Windows. Если после запуска эксперта или индикатора в списке не появился Rterm, значит R-процесс упал. Основная причина, по
которой падает процесс — синтаксическая ошибка в скриптах, несоответствие длин принимающего вектора в MQL и вынимаемого вектора из Rterm-а.
Отлаживать скрипты можно в Rstudio, запуская построчно скрипт от начала до конца.
К сожалению, мне не удалось запустить эксперт в тестере, поэтому тестировать нужно на демо-счете.
4.3. Пути и методы улучшения качественных показателей
- Изменить набор индикаторов используемых на входе.
- Изменить способ нормализации входных данных.
- Оптимизировать параметры "учителя" и индикаторов на входе.
- Изменить кодировку выходной переменной на матрицу с двумя колонками. Калибровать предсказанный сигнал.
- Оптимизировать параметры нейросети (количество нейронов в скрытых слоев, их количество, уровень обучения, количество эпох ).
Заключение
Нами были созданы, обучены и протестированы модели глубоких сетей с инициализацией весов нейронов скрытых слоев от SAE. Сети обучаются действительно быстро, что позволяет переобучать их без остановки процесса торговли.
Результаты, показанные нейросетями, являются средними (имею ввиду метрики). Задача получить идеальный результат не ставилась.
Используя такую модель и постоянное определение коэффициента эффективности, можно оперативно переобучать и оптимизировать модель без прерывания процесса торговли.
Приложения:
- SAE.zip - индикатор, эксперт и сопутствующие файлы (по тексту).
- R_intro.zip - литература по языку R и Rstudio на русском языке.
- DeepLearning.zip - литература по теме "глубокого обучения".
27 ноября 2014, 10:37 Vladimir Perervenko
Последнее редактирование: 2025-11-08
Оценить статью можно после того, как в обсуждении будет хотя бы одно сообщение.Об авторе:
Этот материал взят из в свободном доступе интернета. Вся грамматика источника сохранена.
Тест: А не зомбируют ли меня?
Тест: Определение веса ненаучности