Проблема происхождения интеллекта
Журн. высшей нервн. деятельн. 1998. Т.48. Вып.2. С.358-369.
РЕДЬКО В.Г.
ПРОБЛЕМА ПРОИСХОЖДЕНИЯ ИНТЕЛЛЕКТА И ЭВОЛЮЦИОННАЯ БИОКИБЕРНЕТИКА
Аннотация. В статье развивается предложенная Л.М.Чайлахяном дискуссия, касающаяся проблемы происхождения естественного интеллекта. Аргументируется, что эту проблему целесообразно изучать в рамках общих исследований эволюции биологических информационных и кибернетических систем, таковые исследования могут составлять предмет целой науки - эволюционной биокибернетики.
Цель настоящей статьи - развить дискуссию, предложенную Л.М.Чайлахяном [41], и наметить конструктивные пути исследований эволюции биологических информационных систем. Фактически статья [41] - одна из первых серьезных попыток критически осмыслить с позиций биолога современные бионические исследования, направленные на создание искусственных интеллектуальных информационных систем. В настоящей работе эти же бионические исследования рассматриваются с физико-математической точки зрения.
Сначала - о сравнении точек зрения. Здесь мне не хотелось бы обсуждать спорный вопрос о принципиальной невозможности создания искусственного интеллекта (отметим, что решение этого вопроса во многом зависит от того, что подразумевать под искусственным интеллектом). Однако, я согласен с, как мне кажется, главной идеей работы [41]: современные математические и кибернетические модели биологических информационных систем далеко не отражают их реального биологического значения и функционального предназначения в живых системах. Так же я согласен с тем, что "...проблема происхождения психики - сложнейшая проблема теоретической биологии" [41], и с тем, что для полноценного изучения биологических информационных систем и обеспечиваемых ими кибернетических свойств организмов необходим эволюционный подход, позволяющий осмыслить причины происхождения тех или иных "интеллектуальных изобретений" биологической эволюции. Но я не согласен с несколько скептически-успокоительным настроем статьи [41], подразумевающим, что кибернетические и математические модели в принципе не могут быть адекватны биологическим информационным системам. По моему мнению, сейчас состояние дел в области исследования биологических информационных систем в чем-то напоминает ситуацию в физике в первой половине XVII века, когда, благодаря глубоким исследованиям Г. Галилея и Р. Декарта, работы по созданию физических теорий были уже начаты, однако еще не было Ньютоновских четких и ясных теоретических обобщений, давших толчок дальнейшему развитию точных наук на несколько столетий вперед. По моему мнению, исследования эволюции биологических информационных и кибернетических систем должны составлять предмет целой науки - эволюционной биокибернетики.
Далее в статье будут кратко охарактеризованы направления исследований, которые можно отнести к эволюционной биокибернетике (раздел 2), а также будут предложены некоторые пути дальнейших исследований (раздел 3). Однако, прежде всего остановимся на глубокой гносеологической проблеме, подчеркивающей актуальность исследований, направленных на построение теории эволюционного происхождения логического мышления (раздел 1).
Некоторые обсуждаемые здесь вопросы были рассмотрены в предыдущих работах [29,50].
1. ГНОСЕОЛОГИЧЕСКАЯ ПРОБЛЕМА И ПОДХОДЫ К ЕЕ РЕШЕНИЮ
Существует глубокая гносеологическая проблема: почему человеческая логика применима к познанию природы? Действительно, те процессы, которые происходят в голове ученого, использующего логические методы при изучении природы, совсем не похожи на процессы в исследуемых им явлениях, поэтому применимость нашей логики к этим явлениям далеко не очевидна. В особенности указанная проблема касается применимости математического знания в естественных науках. В этом контексте проблема обсуждалась рядом ученых. Например, М.Клайн в книге “Математика. Поиск истины”, посвященной исследованию природы математического знания, задает вопрос: “Почему теоремы, доказанные человеческим разумом в тиши кабинетов, должны быть применимы к реальному миру...?” [14]. Проблема природы математического знания и удивительной эффективности математики в естественных науках обсуждалась такими известными учеными как А.Пуанкаре и Ю. Вигнер [5,23]. Следует подчеркнуть, что указанная проблема связана с основаниями всего научного познания. В этом разделе делается попытка “нащупать” подходы к решению этой проблемы на естественно-научной основе.
Мне представляется, что наиболее естественный подход к решению рассматриваемой гносеологической проблемы состоит в том, чтобы попытаться разобраться, каким образом в процессе биологической эволюции возникла человеческая логика? Для понимания процесса возникновения логики и осмысления того, как и почему в этом процессе появились логические формы, обеспечивающие познание природы, имеет смысл построить модельную теорию происхождения логики в биосфере. Надежнее всего начать "с самого начала" - с происхождения жизни и проследить весь путь биологической эволюции от простейших до человека, выделяя на этом пути наиболее важные эволюционные "изобретения", ведущие к логике, и осмысливая причины происхождения этих “интеллектуальных изобретений” на базе построения их математических моделей. Чтобы представить круг вопросов, которые могут составить предмет модельной теории происхождения логики, отметим некоторые уровни "интеллектуальных изобретений", укажем соответствующие им примеры и модели, характеризующие эти уровни.
Уровень первый - организм различает состояния внешней среды, память о состояниях записана в геноме и передается по наследству, организм адекватно использует различие сред, меняя свое поведение с изменением среды. Пример этого уровня - свойство регулирования синтеза белков в ответ на изменение питательных веществ во внешней среде по схеме Ф.Жакоба и Ж.Моно [10], которое можно назвать элементарной сенсорикой. Простая математическая модель элементарной сенсорики - адаптивный сайзер (подробнее о сайзерах см. раздел 2), построена в [27].
Второй уровень - временное запоминание организмом состояния среды и адекватное (также временное) приспособление к среде. Пример этого уровня - привыкание, а именно, постепенное угасание реакции раздражения на биологически нейтральный стимул [6,48]. Модели автоматов, способных временно запоминать состояния внешней среды и использовать приобретаемый при этом опыт, уровень "интеллектуальности" которых примерно соответствует уровню привыкания, были разработаны и разносторонне исследованы М.Л.Цетлиным и его последователями [40].
Третий уровень - запоминание устойчивых связей между событиями в окружающей организм природе. Пример - классический условный рефлекс (УР) [22], в котором происходит долговременное запоминание связи между условным и безусловным стимулами. Известен ряд математических и кибернетических моделей УР (популярный обзор моделей сделан в [8]). Однако, насколько мне известно, до сих пор нет математической модели, единым образом отражающей основные свойства УР - самовосстановление, генерализацию, реакцию на дифференцировочные стимулы, и соответствующей биологическому значению УР (предвидение будущих событий и использование этого предвидения).
Между классическим условным рефлексом и логикой лежит ряд промежуточных уровней (инструментальный условный рефлекс, цепи рефлексов и т.д.). Начиная с некоторого уровня, у животных возможно формирование моделей внешнего мира.
Вызывает сомнения возможность построения единой математической модели систем адаптации высших животных лишь потому, что определяющим принципом и направлением этих систем является личностная система значимости, характерная не столько своей сложностью, сколько отсутствием определенной логики для алгоритмизирования, которая не сводится к простому списку произвольных оценок значимости, а, являясь общим и самым главным достижением эволюции данного вида, постоянно находится в тесном соответствии со всем многообразием тех проявлений внешнего мира, с которым сталкивается организм и постоянно меняется вместе с ними и с собственным развитием. В данной статье об этом даже не идет речь.
Последний из
рассматриваемых уровней - логика. Пример этого уровня - системы логического
вывода [9]. Примеры логических правил:  (Если из А следует В , и из В
следует С , то из А следует С ),
(Если из А следует В , и из В
следует С , то из А следует С ),  (Если из А следует В , и В ложно,
то А ложно). Математические модели логики широко разработаны: есть
исчисление высказываний, исчисление предикатов, математические теории
логического вывода [9,15,16]; ведутся работы по формализации индуктивного
вывода [36].
(Если из А следует В , и В ложно,
то А ложно). Математические модели логики широко разработаны: есть
исчисление высказываний, исчисление предикатов, математические теории
логического вывода [9,15,16]; ведутся работы по формализации индуктивного
вывода [36].
Итак, можно выделить несколько ключевых "изобретений" и расположить их в последовательный ряд эволюционных достижений [6] (рис.1). В этом ряду происходит постепенное усовершенствование "познания" закономерностей во внешнем мире. Отметим, что с целью достижения определенности и четкости мы сильно упростили схему развития "интеллектуальных изобретений". В действительности процессы обработки информации и познания закономерностей при “интеллектуальном” поведении животных разного эволюционного уровня, конечно же, значительно сложнее (см., например, [1-3,6,18-21,34]).
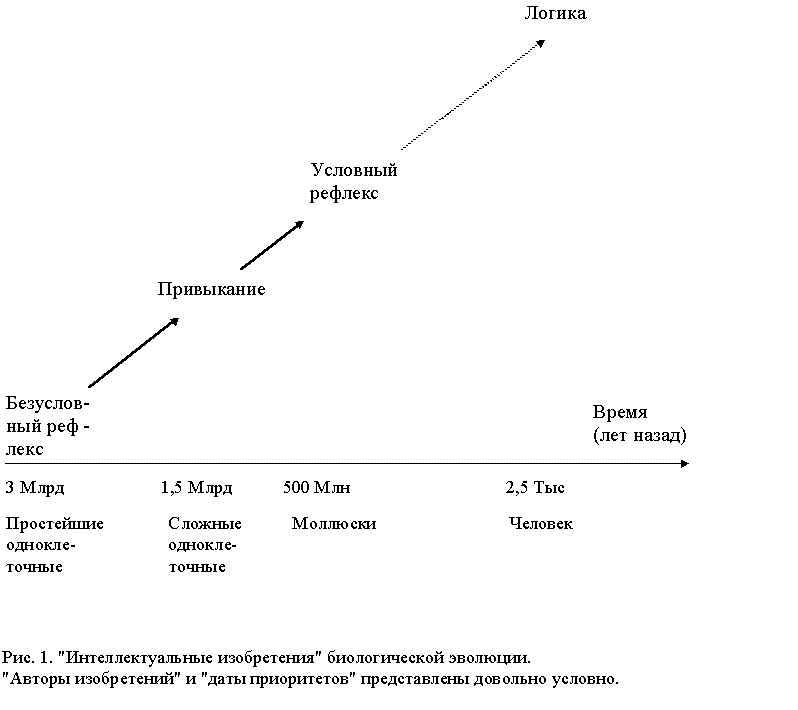
Обратим внимание на фрагментарность и слабую разработанность математических моделей "интеллектуальных изобретений" биологической эволюции. Совершенно нет моделей переходов между "изобретениями" разного уровня. Сейчас можно только предварительно указать на просматриваемые здесь аналогии. Например, выработку условного рефлекса можно рассматривать как происходящий в нервной системе животного элементарный логический вывод - "Если за условным стимулом следует безусловный, а безусловный стимул вызывает определенную реакцию, то условный стимул также вызывает эту реакцию" - дальний предшественник одной из основных формул дедуктивной логики: "Если из А следует В , и из В следует С , то из А следует С ".
Следует отметить, что исследование происхождения логики соответствует определенным тенденциям развития математического знания. Действительно, после открытия И.Ньютоном и Г.Лейбницем дифференциального и интегрального исчисления математики XVII и XVIII веков занимались содержательным развитием и применением этого мощного и плодотворного исчисления, не особенно беспокоясь об его обоснованности. Типичным примером такой позиции служит знаменитое изречение Ж.Даламбера "Идите вперед, и уверенность придет" (цит. по [39]). Но в XIX веке математики устремились к достижению абсолютной строгости. Благодаря работам О.Коши, Б.Больцано, К. Вейерштрасса и других приверженцев строгих доказательств, дифференциальное и интегральное исчисление получает мощное обоснование; в результате был разработан классический математический анализ, сочетающий красоту математической строгости с эффективностью и содержательностью результатов. Затем в начале XX века многие математики обратились к дальнейшему обоснованию математического знания, в том числе к анализу самого инструмента математических исследований - к построению теорий математической логики [9,16]. Т.е. сами математические исследования стали предметом изучения новой дисциплины - теории доказательств или метаматематики [16]. Название метаматематика подчеркивает, что в теории доказательств происходит выход на определенный мета-уровень относительно объекта исследования - собственно математической теории. По-видимому, наиболее естественным продолжением исследований в рамках рассматриваемой тенденции мог бы быть дальнейший переход к более глубокому естественно-научному обоснованию логики путем исследования причин ее происхождения. Подчеркивая, что при этом происходит дальнейший переход на следующий мета-уровень относительно математической логики, теорию происхождения логики можно было бы назвать метаметаматематикой. Т. е., указанная тенденция такова:
математика метаматематика метаметаматематика.
В то время как математическая логика дает ответы на вопросы: "Каковы правила человеческой логики?" и "Как использовать правила логики?", рассматриваемая здесь пока чисто умозрительно теория происхождения логики могла бы дать ответы на более глубокие вопросы: "Почему правила человеческой логики таковы, каковы они есть?" и "Почему правила логики могут корректно использоваться?"
Резюмируя раздел, подчеркнем, что анализ "интеллектуальных изобретений" биологической эволюции и построение теории происхождения логики представляет собой очень интересную и практически нетронутую область для теоретических исследований. Более того, построение теории происхождения логики чрезвычайно актуально в связи с возможностью определенного обоснования всего научного познания.
2. ЭВОЛЮЦИОННАЯ БИОКИБЕРНЕТИКА - СФЕРА ИССЛЕДОВАНИЙ
По моему мнению, теория происхождения логики должна быть важной частью эволюционной биокибернетики. Рис. 2 иллюстрирует области исследований, которые могут быть отнесены к эволюционной биокибернетике.
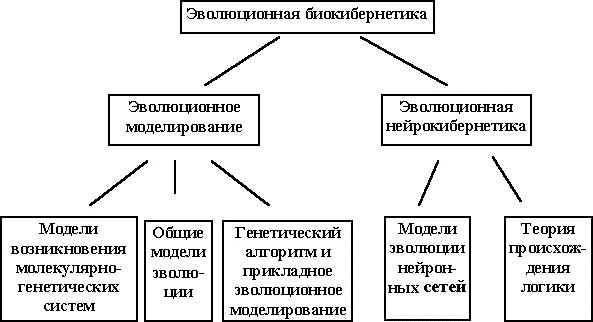
Рис.2. Области исследований эволюционной биокибернетики.
Уже достаточно сложившаяся область - эволюционное моделирование, в котором можно выделить три направления исследований: 1) построение моделей возникновения молекулярно-генетических информационных систем, 2) моделирование общих закономерностей эволюции, 3) прикладное эволюционное моделирование. Охарактеризуем кратко эти направления. Более подробное изложение содержится в [29].
Модели возникновения молекулярно-генетических информационных систем разрабатывались в связи с проблемой происхождения жизни. Проиллюстрируем эти работы на примерах моделей квазивидов и сайзеров.
Модель квазивидов была предложена М.Эйгеном [43]. В этой модели анализируется эволюция популяции последовательностей символов (информационных аналогов цепочек ДНК или РНК). В простейшем случае последовательность символов представляет собой двоичный код, т.е. последовательность нулей и единиц. Последовательности обладают определенными селективными ценностями. Эволюция популяции представляет собой размножение и отбор последовательностей в соответствии с их селективными ценностями, а также мутации, т.е. случайные замены символов в последовательностях. В результате эволюции формируется квазивид: популяция, в которой наряду с оптимальной последовательностью есть множество сходных с ней мутантов. Эйген с сотрудниками провели ряд имитационных расчетов на ЭВМ и продемонстрировали достаточно быструю скорость поиска оптимальных последовательностей в модели квазивидов. В [26] была развита модель квазивидов и получены количественные оценки числа особей, участвующих в эволюционном поиске оптимальных последовательностей. Согласно этим оценкам при эволюционном поиске оптимума число участвующих особей (растущее как небольшая степень длины последовательностей) может быть значительно меньше по сравнению со случайным перебором, при котором число участников экспоненциально растет с ростом длины последовательностей.
Модель сайзеров (syser - сокращение от system of self-reproduction - самовоспроизводящаяся система) была предложена новосибирскими учеными В.А.Ратнером и В.В.Шаминым в 1980 г [24,25]. В простейшем случае эта модель описывает систему макромолекул, в которую входят: полинуклеотидная матрица, ферменты репликации и ферменты трансляции; полинуклеотидная матрица хранит информацию, кодирующую синтезируемые в сайзере ферменты, ферменты репликации обеспечивают копирование полинуклеотидных цепочек, а ферменты трансляции - синтез ферментов в соответствии с закодированной в матрице информацией. Сайзеры - вполне естественная модель простейшей самовоспроизводящейся системы, поэтому неудивительно, что она под разными названиями и в несколько различных формах была предложена независимо от Ратнера и Шамина и другими авторами: Д.Уайтом [51] и Р.Файстелем [46]. По общей структуре модель сайзеров сходна со схемой самовоспроизводящихся автоматов, исследованных на заре развития вычислительной техники Дж.фон Нейманом [38]. Самовоспроизводящиеся автоматы по фон Нейману содержат хранящую информацию ленту (аналог полинуклеотидной матрицы), автомат для копирования ленты (аналог ферментов репликации) и автомат для синтеза произвольного автомата по закодированной в ленте информации (аналог ферментов трансляции). Концепция биологических информационных систем, основанная на аналогиях с самовоспроизводящимися автоматами фон Неймана, разработана В.И.Корогодиным [17].
Среди работ, посвященных моделированию общих кибернетических закономерностей биологической эволюции, отметим интересный цикл исследований С.Кауффмана, посвященный анализу автоматов, состоящих из множества случайно связанных логических элементов [13]. Отдельный автомат можно рассматривать как модель молекулярно-генетической системы управления живой клетки, при этом каждый логический элемент интерпретируется как регулятор синтеза определенного фермента. Примечательно, что при исследовании автоматов Кауффмана применяются высокоэффективные математические методы статистической физики. Модели Кауффмана позволяют сделать ряд предсказаний относительно "программ" жизнедеятельности клеток. В частности, продемонстрировано, что для одновременного обеспечения устойчивости и гибкости программы число входов логических элементов должно быть ограничено определенным интервалом, а именно составлять величину примерно равную 2-3.
К работам по моделированию общих аспектов биологической эволюции можно отнести и исследования вопросов эволюции генетических текстов. Например, в работах Д.С.Чернавского и Н.М. Чернавской [42] исследовалась проблема возникновения в процессе эволюции новой биологически значимой информации, а также была сделана оценка вероятности случайного формирования в геноме участка ДНК, кодирующего новый функционально важный для организма белок. Интересна, хотя, по-видимому, не бесспорна, модель блочно-иерархического эволюционного отбора [11], согласно которой новые генетические тексты большой длины сначала случайно составляются из коротких текстов, оптимизированных в предыдущие эволюционные эпохи, а после составления оптимизируются.
Прикладное эволюционное моделирование связано с идеей: можно ли использовать принципы биологической эволюции для оптимизации практически важных для человека систем? В нескольких модификациях основанные на таких идеях исследования проводились рядом авторов. В 60-х годах Л.Фогель, А.Оуенс, М.Уолш предложили схему эволюции логических автоматов, решающих задачи прогноза [37]. Исследования по прикладному эволюционному моделированию, идейно близкие к работам Фогеля с сотрудниками, были разносторонне развиты в работах И.Л.Букатовой [4]. В последнее время проявляется большой интерес к исследованию и использованию генетического алгоритма, предложенного Дж.Холландом [47]. Общая схема генетического алгоритма практически совпадает с таковой в модели квазивидов, за исключением того, что в генетическом алгоритме механизм изменчивости помимо точечных мутаций (равновероятных случайных замен символов информационных последовательностей - аналогов геномов "особей") включает в себя кроссинговер - скрещивание последовательностей, и инверсии - обращение порядка следования символов в некотором случайно выбранном участке последовательности.
Сфера применений генетического алгоритма обширна: это и разработка экспертных систем в искусственном интеллекте, и сугубо практическая оптимизация работы нефтяных трубопроводов, и моделирование структур нейронных сетей в нейрокибернетических исследованиях.
Вторая область исследований, которую можно отнести к эволюционной биокибернетике - эволюционная нейрокибернетика, а именно исследования по эволюции информационных процессов в нервной системе. В отличие от эволюционного моделирования эта область исследований только формируется. К ней можно отнести работы по моделированию эволюции нейронных сетей и собственно теорию происхождения логики, подходы к построению которой обсуждались в разделе 1.
Говоря о нейронных сетях, нельзя не отметить чрезвычайно широкого развития нейросетевых моделей в последние 10-15 лет. В моделях строятся сети из формальных нейронов (многовходовых пороговых элементов). Специалисты по нейронным сетям разработали эффективные алгоритмы ассоциативной памяти, распознавания образов, обработки информации в системах управления. Достоинства нейронных сетей - параллельность обработки информации и способность к обучению.
Работы по моделированию эволюции нейронных сетей включают в себя как разработку концепций селективного отбора эффективных нейронных сетей при обучении животных [44,45], так и анализ возможностей эволюционной оптимизации нейронных сетей с помощью генетического алгоритма или его аналогов [35].
3. ПОДХОДЫ К ДАЛЬНЕЙШЕМУ МОДЕЛИРОВАНИЮ
Теперь, кратко охарактеризовав ключевую проблему и направления работ эволюционной биокибернетики, наметим некоторые пути дальнейших исследований, которые в определенной степени могут прояснить вопросы, поставленные в [41].
Интересно промоделировать возникновение и развитие целенаправленного поведения животных, адекватно учитывая такие важные свойства, как потребность, мотивация, доминанта. Значимость этих свойств для функционирования биологических информационных систем подчеркивалась рядом авторов [2,17,31-34,49].
Рассмотрим сначала простую модель возникновения целенаправленного поведения. Представим себе примитивное животное, имеющее как минимум две потребности и рассмотрим схему управления поведением, направленным на удовлетворение этих двух потребностей. В качестве опорного примера будем подразумевать, что потребности соответствуют двум типам питательных веществ, которые необходимо получать животному. Будем предполагать, что:
1) каждая из потребностей характеризуется своим ресурсом ri , i - номер потребности, i = 1, 2 (рис. 3);
2) животное может определять наличие во внешней среде E ситуаций, позволяющих удовлетворять потребности (в нашем опорном случае - наличие двух типов питательных веществ);
3) с помощью управляющих блоков Ui животное может включать систему действий Ai , направленных на удовлетворение первой и второй потребности, выполняя эти действия, животное тем самым пополняет ресурсы ri ;
4) для выполнения действий Ai животное должно привлекать свои общие ресурсы Rg (для рассматриваемого примера считаем, что Rg - ресурсы, обеспечивающие перемещение животного).
|
а |
б |
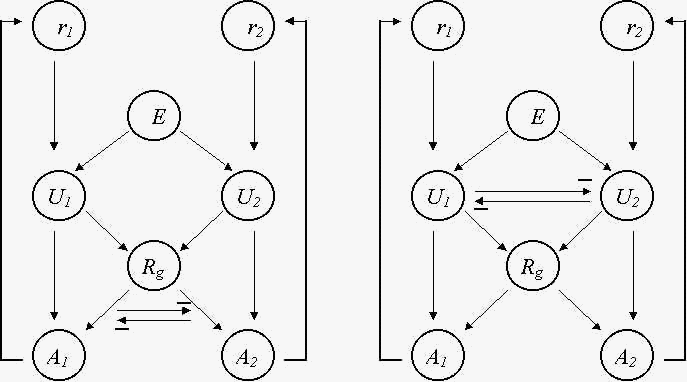
Рис. 3. Схема управления поведением, направленным на удовлетворение двух потребностей. Взаимное торможение осуществляется на уровне действий (а), либо на уровне управляющих блоков (б). ri - ресурсы потребностей, i = 1, 2; E - внешняя среда; Ui - управляющие блоки; Rg - общие ресурсы животного; Ai - действия, направленные на удовлетворение потребностей.
При недостатке первого ресурса r1 и наличии соответствующего питательного вещества во внешней среде E управляющий блок U1 включает систему действий A1 , привлекая при этом общий ресурс Rg . Однако, если одновременно выполняются аналогичные условия для второй потребности, то управляющий блок U2 включает свою систему действий A2 , и возникает конкуренция за общий ресурс, которая препятствует удовлетворению обоих потребностей (рис. 3а). Для рассматриваемого опорного примера возможна ситуация (два типа питательных веществ находятся по разные стороны от животного), когда из-за конкуренции ни одна из потребностей не может быть удовлетворена.
Устранить влияние конкуренции на уровне действий можно, введя конкуренцию на уровне управляющих блоков, а именно, введя взаимное торможение между блоками U1 и U2 (рис. 3б). В этом случае только один из управляющих блоков U1 , либо U2 , соответствующий приоритетной потребности, включает действие A1 , либо A2 , т.е. действия A1 и A2 могут выполняться только последовательно, тем самым животное сначала обеспечивает достижение одной (наиболее приоритетной) цели, а затем другой (которая в свою очередь становится приоритетной после выполнения первого действия и пополнения соответствующего ресурса).
Переход к схеме с тормозящими связями на уровне управляющих блоков (рис. 3б) от схемы, представленной на рис. 3а, можно рассматривать как простую модель возникновения доминанты. Вводя количественные параметры, характеризующие ресурсы, управляющие сигналы, коэффициенты связей между блоками, частоты появления питательных веществ во внешней среде, можно построить математические модели обеих рассматриваемых схем, провести детальный анализ их функционирования и выяснить условия (соотношения между параметрами), при которых возникновение доминанты селективно выгодно.
Схема управления, изображенная на рис. 3б, довольно проста, не подразумевает запоминания индивидуальных приобретенных навыков и, в принципе, могла бы возникнуть у одноклеточных организмов на молекулярно-генетическом уровне.
Более сложная схема, включающая использование индивидуальной памяти животного, прогноз результата мотивированного действия, принятие решения, сравнение результата действия с прогнозом и (при необходимости) коррекцию действия, - функциональная система по П.К. Анохину [2]. Построение и исследование математических моделей функциональных систем в духе Анохина - одно из естественных направлений исследований, которые могут быть проведены в ближайшее время.
Простейшая модель функциональной системы могла бы описывать систему управления, обеспечивающую удовлетворение нескольких потребностей на основе использования кратковременной и долговременной ассоциативной памяти, и характеризовать такие свойства как привыкание и условные рефлексы.
Функциональные системы обладают хорошим потенциалом для будущего развития кибернетических моделей. В общую схему функциональной системы помимо основных потребностей могут быть включены подпотребности (например, необходимость избежать боль - подпотребность сохранения организма); в памяти могут формироваться модели ситуаций во внешней среде в виде семантических сетей [12], характеризующих смысловые связи между различными объектами во внешней среде [7] (для достаточно высокого уровня животных в памяти могут формироваться парадигмы - общие картины внешнего мира); принятие решений может включать логические выводы на семантических сетях; достижение основных целей может включать выделение и достижение промежуточных подцелей.
Один из наиболее интересных вопросов, обсуждавшихся в [41], - как биологические информационные системы могли возникать естественным путем, в процессе самоорганизации. Иначе этот вопрос можно переформулировать так: можно ли промоделировать процесс возникновения новой информационной системы, "не навязывая своей воли" этому процессу, не зная заранее, что получится?
Прямой путь к такому моделированию - непосредственная имитация эволюционного процесса. Пример - модель возникновения "программ жизнедеятельности" одноклеточных организмов [28]. Эта модель основана на следующих предположениях: 1) геном организма кодирует систему регуляторно взаимодействующих между собой ферментов (регулирование синтеза ферментов аналогично таковому в схеме Жакоба и Моно [10]); 2) в процессе эволюции в геноме организмов-потомков могут появляться или исчезать участки, кодирующие ферменты, появляющиеся таким образом новые ферменты случайно взаимодействуют с уже имеющимися; 3) для фиксированного организма в каждый момент времени в результате положительных и отрицательных регуляторных взаимодействий синтезируется только часть из кодируемых геномом ферментов; синтезируемый в данный момент времени ферментный набор характеризует состояние организма; 4) последовательность чередующихся во времени состояний организма (ферментных наборов) представляет собой повторяющийся цикл или "программу жизнедеятельности" организма; 5) приспособленность организма пропорциональна отношению длины жизненного цикла к общему числу ферментов в организме (такое определение приспособленности нейтрально и не имеет какой-либо связи с конкретными свойствами ферментов, т. е. при моделировании не происходит “навязывания своей воли” эволюционному процессу). Моделирование проводилось путем имитации эволюционного процесса на ЭВМ. В процессе эволюции отбирались организмы, обладающие достаточно нетривиальными программами жизнедеятельности (жизненный цикл состоял из нескольких десятков состояний при примерно десяти ферментах в организме). В модель вводились также "удары судьбы", которые случайным образом частично меняли взаимодействие между ферментами (это можно интерпретировать как попадание в среду обитания организмов новых химических веществ, которые случайно меняют каталитические свойства ферментов). Под действием ударов судьбы программы жизнедеятельности частично разрушались, однако, возникающие в процессе последующей эволюции новые программы включали в себя отдельные блоки старых программ, т.е. программы формировались не полностью оптимально, а по возможности оптимально, насколько это позволял имеющийся "подручный материал". В целом модель возникновения программ жизнедеятельности [28] соответствует описанной в [41] стратегии одноклеточного организма, за исключением того, что эта модель не учитывает указанного в [41] управляющего влияния внешних химических веществ на синтез ферментов внутри клетки.
Отметим, что имитация эволюционных процессов возможна не только на базе программ для универсальных ЭВМ, но и с использованием параллельно функционирующих специализированных эволюционных оптимизаторов [30], применение которых могло бы радикально ускорить процессы моделирования.
Подводя итог, подчеркну основные моменты. По моему мнению, наиболее естественный путь к пониманию информационных и кибернетических свойств биологических организмов - построение базовых математических моделей, адекватно характеризующих основные ступени развития "интеллектуальных изобретений" биологической эволюции. Область этих исследований чрезвычайно обширна и требует энергичных совместных действий биологов и кибернетиков.
Автор благодарен К.А.Никольской за плодотворные дискуссии.
Список литературы
1. Андрианов О.С. Организованный мозг ( очерк о конструкции и функциональной организации мозга) // Успехи физиол. наук. 1995. Т.26. № 1. С. 25 (Сообщение 1), Успехи физиол. наук. 1995. Т.26. № 2. С. 18 (Сообщение 2).
2. Анохин П.К. Системные механизмы высшей нервной деятельности. М.: Наука, 1979. 453 с.
3. Балабан П.М. Концепция подкрепления на простых нервных системах // Журн. высш. нерв. деят. 1997. Т.47. № 2. С. 280.
4. Букатова И.Л. Эволюционное моделирование и его приложения. М.: Наука, 1979. 231 с.
5. Вигнер Ю. Непостижимая эффективность математики в естественных науках // Вигнер Ю. Этюды о симметрии. М.: Мир, 1971. С. 182.
6. Воронин Л.Г. Эволюция высшей нервной деятельности. М.: Наука, 1977, 128 с.
7. Воронин Л.Г., Никольская К.А. О структурной организации памяти // Нейрофизиологические основы памяти. 7-е гагрские беседы. Тбилиси: Мецниереба, 1979. С. 345.
8. Гаазе-Раппопорт М.Г., Поспелов Д.А. От амебы до робота: модели поведения. М.: Наука, 1987. 288 с.
9. Генцен Г. Исследования логических выводов // Математическая теория логического вывода. М.: Наука, 1967. С. 9.
10. Жакоб Ф., Моно Ж. Регуляция активности генов // Регуляторные системы клетки. М.: Мир, 1964. С. 278.
11. Иваницкий Г.Р., Есипова Н.Г., Абагян Р.А., Шноль С.Э. Блочное совершенствование генетического текста как фактор ускорения биологической эволюции // Биофизика. 1985. Т.30. № 3. С. 418.
12. Искусственный интеллект. - В 3-х кн. Кн.2. Модели и методы. Справочник / Под ред. Д.А.Поспелова. М.: Радио и связь, 1990. 304 с.
13. Кауффман С. Антихаос и приспособление // В мире науки. 1991. № 10. С. 58.
14. Клайн М. Математика. Поиск истины. М.: Мир, 1988. 295 с.
15. Клини С. Математическая логика. М.: Мир, 1973. 480 с.
16. Клини С. Введение в метаматематику. М.: ИЛ. 1957. 526 c.
17. Корогодин В.И. Информация и феномен жизни. Пущино, 1991, 202 с.
18. Костандов Э.А. Установка как физиологическая детерминанта поведения // Журн. высш. нерв. деят. 1995. Т.45. № 1. С. 3.
19. Крушинский Л.В. Биологические основы рассудочной деятельности: эволюционные и физиологическо-генетические аспекты. М.: Изд-во Московского университета, 1986. 270 с.
20. Леонтьев А.Н. Проблемы развития психики. М.: Изд-во Московского университета, 1981. 584 с.
21. Никольская К.А., Савоненко А.В., Осипов А.И., Ещенко О.В., Карась А.Я. Информационная роль инстинкта при организации целенаправленного поведения // Успехи совр. биологии. 1995. Т.115. № 4. С. 390.
22. Павлов И.П. Двадцатилетний опыт объективного изучения высшей нервной деятельности (поведения) животных. Условные рефлексы. М., Л.: Госиздат, 1928. 388 с.
23. Пуанкаре А. О науке. М.: Наука, 1990. 736 с.
24. Ратнер В.А., Шамин В.В. Сайзеры: моделирование фундаментальных особенностей молекулярно-биологической организации // Математические модели эволюционной генетики. Новосибирск: ИЦИГ, 1980. С. 66.
25. Ратнер В.А., Шамин В.В. Сайзеры: моделирование фундаментальных особенностей молекулярно-биологической организации. Соответствие общих свойств и конструктивных особенностей коллективов макромолекул // Журн. общ. биологии. 1983. Т.44. № 1. С. 51.
26. Редько В.Г. Спиновые стекла и эволюция // Биофизика. 1990. Т.35. № 5. С. 831.
27. Редько В.Г. Адаптивный сайзер // Биофизика. 1990. Т.35. № 6. С. 1007.
28. Редько В.Г. К теории эволюции. Модель возникновения “программ жизнедеятельности” // Журн. общ. биологии. 1991. Т.52. № 3. С. 334.
29. Редько В.Г. Эволюционный подход к исследованию естественных и созданию искусственных “биокомпьютеров” // Нейрокомпьютер. 1994. № 1,2. С. 38.
30. Редько В.Г., Дябин М.И., Елагин В.М., Карпинский Н.Г., Половянюк А.И., Сереченко В.А., Ургант О.В. К микроэлектронной реализации эволюционного оптимизатора // Микроэлектроника. 1995. Т. 24. № 3. С. 207.
31. Симонов П.В. Доминанта и нейродарвинизм // Журн. высш. нерв. деят. 1993. Т.43. № 4. С. 765.
32. Судаков К.В. Мотивация и подкрепление в системных механизмах поведения: динамические энграммы поведения // Журн. высш. нерв. деят. 1995. Т.45. № 4. С. 627.
33. Судаков К.В. Системный процесс подкрепления // Журн. высш. нерв. деят. 1996. Т.46. № 4. С. 643.
34. Судаков К.В. Пластичность системных механизмов мозга // Успехи физиол. наук. 1996. Т.27. № 2. С. 3.
35. Терехин А.Т. , Будилова Е. В. Сетевые механизмы физиологической регуляции // Успехи физиол. наук. 1995. Т. 26. № 4. С. 75.
36. Финн В.К. О машинно ориентированной формализации правдоподобных рассуждений в стиле Ф. Бэкона - Д.С. Милля // Семиотика и информатика. 1983. М.: ВИНИТИ. Вып. 20. С. 35.
37. Фогель Л., Оуэнс А., Уолш М. Искусственный интеллект и эволюционное моделирование. М.: Мир, 1969. 230 с.
38. Фон Нейман Дж. Теория самовоспроизводящихся автоматов. М.: Мир, 1971. 382 с.
39. Френкель А., Бар-Хиллел И. Основания теории множеств. М.: Мир, 1966. 556 с.
40. Цетлин М.Л. Исследования по теории автоматов и моделирование биологических систем. М.: Наука, 1969. 316 с.
41. Чайлахян Л. М. Информационно-энергетическая концепция происхождения психики // Журн. высш. нерв. деят. 1996. Т.46. № 3. С. 617.
42. Чернавская Н.М., Чернавский Д.С. Проблема возникновения новой информации в эволюции // Термодинамика и регуляция биологических процессов. Теория информации, управление в живых системах, проблема самоорганизации, эволюция и онтогенез. М.: Наука, 1984. С. 247.
43. Эйген М., Шустер П. Гиперцикл. Принципы самоорганизации макромолекул. М.: Мир, 1982. 270 с.
44. Conrad M. Evolutionary learning circuits // J. Theor. Biol. 1974. V.46. № 1. P. 167.
45. Edelman G. M. Neural Darwinism. The theory of neural group selection. N.Y. : Basic Books, 1987. 371 p.
46. Feistel R. On the evolution of biological macromolecules. Precelular organization. 4. Holobiotic competition // Studia biophysica. 1983. V.93. № 2. P. 113.
47. Holland J.H. Adaptation in natural and artificial systems. Ann Arbor: Univ. of Michigan Press, 1975. 183 p.
48. Kinastowski W. Der Einfluss der mechanishcen Reise auf die Kontraktilitat von Spirotomum ambguum Ehrbg. // Acta Protozool. 1963. V.1. Fasc. 23. P. 201.
49. Kryukov V.I. An attention model based on the principle of dominanta // Proceedings in Nonlinear Science. Neurocomputers and Attention. I: Neurobiology, Synchronization, and Chaos. 1989. Ed by A.Y. Holden and V.I.Kryukov. P. 319.
50. Red'ko V.G. Towards the evolutionary biocybernetics // Proceedings of The Second International Symposium on Neuroinformatics and Neurocomputers, Rostov-on-Don, 1995. P. 422.
51. White D.H. A theory for the origin of the self-replicating chemical system. 1. Natural selection of the autogen from short random oligomers // J. Mol. Evol. 1980. V.16. № 2. P. 121.
Физико-технологический институт РАН, Москва
