Искусственные нейронные сети
Введение в искусственные нейронные сети
|
17.04.1997 |
|
Анил
К. Джейн Мичиганский Государственный университет, США jain@cps.msu.edu Жианчанг Мао, К М. Моиуддин Исследовательский Центр IBM в Альмадене, США |
|
Anil K. Jain, Jianchang Mao, K.M. Mohiuddin
Artificial Neural Networks: A Tutorialп,
Computer, Vol.29, No.3, March/1996, pp. 31-44.
Translated from the original English version and reprinted with permission. (IEEE) |
Интеллектуальные системы на основе искусственных нейронных сетей (ИНС) позволяют с успехом решать проблемы распознавания образов, выполнения прогнозов, оптимизации, ассоциативной памяти и управления. Известны и иные, более традиционные подходы к решению этих проблем, однако они не обладают необходимой гибкостью за пределами ограниченных условий. ИНС дают многообещающие альтернативные решения, и многие приложения выигрывают от их использования. Данная статья является введением в современную проблематику ИНС и содержит обсуждение причин их стремительного развития. Здесь описаны также основные принципы работы биологического нейрона и его искусственной вычислительной модели. Несколько слов будет сказано о нейросетевых архитектурах и процессах обучения ИНС. Венчает статью знакомство с проблемой распознавания текста - наиболее успешной реализацией ИНС.
Длительный период эволюции придал мозгу человека много качеств, которые отсутствуют как в машинах с архитектурой фон Неймана, так и в современных параллельных компьютерах. К ним относятся:
массовый параллелизм,
распределенное представление информации и вычисления,
способность к обучению и способность к обобщению,
адаптивность,
свойство контекстуальной обработки информации,
толерантность к ошибкам,
низкое энергопотребление.
Можно предположить, что приборы, построенные на тех же принципах, что и биологические нейроны, будут обладать перечисленными характеристиками.
1. От биологических сетей к ИНС
Современные цифровые вычислительные машины превосходят человека по способности производить числовые и символьные вычисления. Однако человек может без усилий решать сложные задачи восприятия внешних данных (например, узнавание человека в толпе только по его промелькнувшему лицу) с такой скоростью и точностью, что мощнейший в мире компьютер по сравнению с ним кажется безнадежным тугодумом. В чем причина столь значительного различия в их производительности? Архитектура биологической нейронной системы совершенно не похожа на архитектуру машины фон Неймана (Таблица 1), существенно влияет на типы функций, которые более эффективно исполняются каждой моделью.
Таблица 1.
Машина
фон Неймана по сравнению с биологической нейронной системой.
|
|
Машина фон Неймана |
Биологическая нейронная система |
|
Процессор |
Сложный |
Простой |
|
Высокоскоростной |
Низкоскоростной |
|
|
Один или несколько |
Большое количество |
|
|
Память |
Отделена от процессора |
Интегрирована в процессор |
|
Локализована |
Распределенная |
|
|
Адресация не по содержанию |
Адресация по содержанию |
|
|
Вычисления |
Централизованные |
Распределенные |
|
Последовательные |
Параллельные |
|
|
Хранимые программы |
Самообучение |
|
|
Надежность |
Высокая уязвимость |
Живучесть |
|
Специализация |
Численные и символьные oперации |
Проблемы восприятия |
|
Среда функционирования |
Строго определенная |
Плохо определенная |
|
Строго ограниченная |
Без ограничений |
Подобно биологической нейронной системе ИНС является вычислительной системой с огромным числом параллельно функционирующих простых процессоров с множеством связей. Модели ИНС в некоторой степени воспроизводят "организационные" принципы, свойственные мозгу человека. Моделирование биологической нейронной системы с использованием ИНС может также способствовать лучшему пониманию биологических функций. Такие технологии производства, как VLSI (сверхвысокий уровень интеграции) и оптические аппаратные средства, делают возможным подобное моделирование.
Глубокое изучение ИНС требует знания нейрофизиологии, науки о познании, психологии, физики (статистической механики), теории управления, теории вычислений, проблем искусственного интеллекта, статистики/математики, распознавания образов, компьютерного зрения, параллельных вычислений и аппаратных средств (цифровых/аналоговых/VLSI/оптических). С другой стороны, ИНС также стимулируют эти дисциплины, обеспечивая их новыми инструментами и представлениями. Этот симбиоз жизненно необходим для исследований по нейронным сетям.
Представим некоторые проблемы, решаемые в контексте ИНС и представляющие интерес для ученых и инженеров.
Классификация образов. Задача состоит в указании принадлежности входного образа (например, речевого сигнала или рукописного символа), представленного вектором признаков, одному или нескольким предварительно определенным классам. К известным приложениям относятся распознавание букв, распознавание речи, классификация сигнала электрокардиограммы, классификация клеток крови.
Кластеризация/категоризация. При решении задачи кластеризации, которая известна также как классификация образов "без учителя", отсутствует обучающая выборка с метками классов. Алгоритм кластеризации основан на подобии образов и размещает близкие образы в один кластер. Известны случаи применения кластеризации для извлечения знаний, сжатия данных и исследования свойств данных.
Аппроксимация функций. Предположим, что имеется обучающая выборка ((x1,y1), (x2,y2)..., (xn,yn)) (пары данных вход-выход), которая генерируется неизвестной функцией (x), искаженной шумом. Задача аппроксимации состоит в нахождении оценки неизвестной функции (x). Аппроксимация функций необходима при решении многочисленных инженерных и научных задач моделирования.
Предсказание/прогноз. Пусть заданы n дискретных отсчетов {y(t1), y(t2)..., y(tn)} в последовательные моменты времени t1, t2,..., tn . Задача состоит в предсказании значения y(tn+1) в некоторый будущий момент времени tn+1. Предсказание/прогноз имеют значительное влияние на принятие решений в бизнесе, науке и технике. Предсказание цен на фондовой бирже и прогноз погоды являются типичными приложениями техники предсказания/прогноза.
Оптимизация. Многочисленные проблемы в математике, статистике, технике, науке, медицине и экономике могут рассматриваться как проблемы оптимизации. Задачей алгоритма оптимизации является нахождение такого решения, которое удовлетворяет системе ограничений и максимизирует или минимизирует целевую функцию. Задача коммивояжера, относящаяся к классу NP-полных, является классическим примером задачи оптимизации.
Память, адресуемая по содержанию. В модели вычислений фон Неймана обращение к памяти доступно только посредством адреса, который не зависит от содержания памяти. Более того, если допущена ошибка в вычислении адреса, то может быть найдена совершенно иная информация. Ассоциативная память, или память, адресуемая по содержанию, доступна по указанию заданного содержания. Содержимое памяти может быть вызвано даже по частичному входу или искаженному содержанию. Ассоциативная память чрезвычайно желательна при создании мультимедийных информационных баз данных.
Управление. Рассмотрим динамическую систему, заданную совокупностью {u(t), y(t)}, где u(t) является входным управляющим воздействием, а y(t) - выходом системы в момент времени t. В системах управления с эталонной моделью целью управления является расчет такого входного воздействия u(t), при котором система следует по желаемой траектории, диктуемой эталонной моделью. Примером является оптимальное управление двигателем.
1.1 Краткий исторический обзор
Исследования в области ИНС пережили три периода активизации. Первый пик в 40-х годах обусловлен пионерской работой МакКаллока и Питтса [4]. Второй возник в 60-х благодаря теореме сходимости перцептрона Розенблатта [5] и работе Минского и Пейперта [6], указавшей ограниченные возможности простейшего перцептрона. Результаты Минского и Пейперта погасили энтузиазм большинства исследователей, особенно тех, кто работал в области вычислительных наук. Возникшее в исследованиях по нейронным сетям затишье продлилось почти 20 лет. С начала 80-х годов ИНС вновь привлекли интерес исследователей, что связано с энергетическим подходом Хопфилда [7] и алгоритмом обратного распространения для обучения многослойного перцептрона (многослойные сети прямого распространения), впервые предложенного Вербосом [8] и независимо разработанного рядом других авторов. Алгоритм получил известность благодаря Румельхарту [9] в 1986году Андерсон и Розенфельд [10] подготовили подробную историческую справку о развитии ИНС.
1.2 Биологические нейронные сети
Нейрон (нервная клетка) является особой биологической клеткой, которая обрабатывает информацию (рис. 1). Она состоит из тела клетки (cell body), или сомы (soma), и двух типов внешних древоподобных ветвей: аксона (axon) и дендритов (dendrites). Тело клетки включает ядро (nucleus), которое содержит информацию о наследственных свойствах, и плазму, обладающую молекулярными средствами для производства необходимых нейрону материалов. Нейрон получает сигналы (импульсы) от других нейронов через дендриты (приемники) и передает сигналы, сгенерированные телом клетки, вдоль аксона (передатчик), который в конце разветвляется на волокна (strands). На окончаниях этих волокон находятся синапсы (synapses).
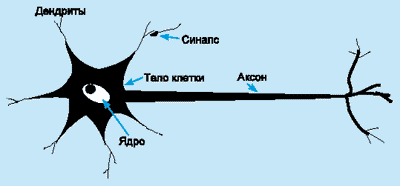
Рисунок 1.
Схема
биологического нейрона.
Синапс является элементарной структурой и функциональным узлом между двумя нейронами (волокно аксона одного нейрона и дендрит другого). Когда импульс достигает синаптического окончания, высвобождаются определенные химические вещества, называемые нейротрансмиттерами. Нейротрансмиттеры диффундируют через синаптическую щель, возбуждая или затормаживая, в зависимости от типа синапса, способность нейрона-приемника генерировать электрические импульсы. Результативность синапса может настраиваться проходящими через него сигналами, так что синапсы могут обучаться в зависимости от активности процессов, в которых они участвуют. Эта зависимость от предыстории действует как память, которая, возможно, ответственна за память человека.
Кора головного мозга человека является протяженной, образованной нейронами поверхностью толщиной от 2 до 3 мм с площадью около 2200 см2, что вдвое превышает площадь поверхности стандартной клавиатуры. Кора головного мозга содержит около 10^11 нейронов, что приблизительно равно числу звезд Млечного пути [11]. Каждый нейрон связан с 10^3 - 10^4 другими нейронами. В целом мозг человека содержит приблизительно от 10^14 до 10^15 взаимосвязей.
Нейроны взаимодействуют посредством короткой серии импульсов, как правило, продолжительностью несколько мсек. Сообщение передается посредством частотно-импульсной модуляции. Частота может изменяться от нескольких единиц до сотен герц, что в миллион раз медленнее, чем самые быстродействующие переключательные электронные схемы. Тем не менее сложные решения по восприятию информации, как, например, распознавание лица, человек принимает за несколько сотен мс. Эти решения контролируются сетью нейронов, которые имеют скорость выполнения операций всего несколько мс. Это означает, что вычисления требуют не более 100 последовательных стадий. Другими словами, для таких сложных задач мозг "запускает" параллельные программы, содержащие около 100 шагов. Это известно как правило ста шагов [12]. Рассуждая аналогичным образом, можно обнаружить, что количество информации, посылаемое от одного нейрона другому, должно быть очень маленьким (несколько бит). Отсюда следует, что основная информация не передается непосредственно, а захватывается и распределяется в связях между нейронами. Этим объясняется такое название, как коннекционистская модель, применяемое к ИНС.
2. Основные понятия
2.1 Модель технического нейрона
МакКаллок и Питтс [4] предложили использовать бинарный пороговый элемент в качестве модели искусственного нейрона. Этот математический нейрон вычисляет взвешенную сумму n входных сигналов xj, j = 1, 2... n, и формирует на выходе сигнал величины 1, если эта сумма превышает определенный порог u, и 0 - в противном случае.
Часто удобно рассматривать u как весовой коэффициент, связанный с постоянным входом x0 = 1. Положительные веса соответствуют возбуждающим связям, а отрицательные - тормозным. МакКаллок и Питтс доказали, что при соответствующим образом подобранных весах совокупность параллельно функционирующих нейронов подобного типа способна выполнять универсальные вычисления. Здесь наблюдается определенная аналогия с биологическим нейроном: передачу сигнала и взаимосвязи имитируют аксоны и дендриты, веса связей соответствуют синапсам, а пороговая функция отражает активность сомы.
2.2 Архитектура нейронной сети
ИНС может рассматриваться как направленный граф со взвешенными связями, в котором искусственные нейроны являются узлами. По архитектуре связей ИНС могут быть сгруппированы в два класса (рис. 2): сети прямого распространения, в которых графы не имеют петель, и рекуррентные сети, или сети с обратными связями.
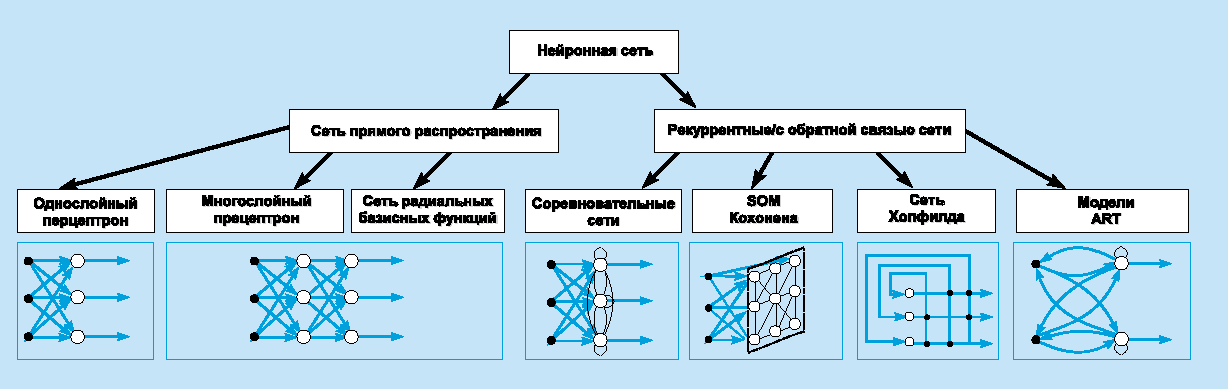
Рисунок 2.
Систематизация
архитектур сетей прямого распространения и рекуррентных (с обратной связью).
В наиболее распространенном семействе сетей первого класса, называемых многослойным перцептроном, нейроны расположены слоями и имеют однонаправленные связи между слоями. На рис. 2 представлены типовые сети каждого класса. Сети прямого распространения являются статическими в том смысле, что на заданный вход они вырабатывают одну совокупность выходных значений, не зависящих от предыдущего состояния сети. Рекуррентные сети являются динамическими, так как в силу обратных связей в них модифицируются входы нейронов, что приводит к изменению состояния сети.
2.3 Обучение
Способность к обучению является фундаментальным свойством мозга. В контексте ИНС процесс обучения может рассматриваться как настройка архитектуры сети и весов связей для эффективного выполнения специальной задачи. Обычно нейронная сеть должна настроить веса связей по имеющейся обучающей выборке. Функционирование сети улучшается по мере итеративной настройки весовых коэффициентов. Свойство сети обучаться на примерах делает их более привлекательными по сравнению с системами, которые следуют определенной системе правил функционирования, сформулированной экспертами.
Для конструирования процесса обучения, прежде всего, необходимо иметь модель внешней среды, в которой функционирует нейронная сеть - знать доступную для сети информацию. Эта модель определяет парадигму обучения [3]. Во-вторых, необходимо понять, как модифицировать весовые параметры сети - какие правила обучения управляют процессом настройки. Алгоритм обучения означает процедуру, в которой используются правила обучения для настройки весов.
Существуют три парадигмы обучения: "с учителем", "без учителя" (самообучение) и смешанная. В первом случае нейронная сеть располагает правильными ответами (выходами сети) на каждый входной пример. Веса настраиваются так, чтобы сеть производила ответы как можно более близкие к известным правильным ответам. Усиленный вариант обучения с учителем предполагает, что известна только критическая оценка правильности выхода нейронной сети, но не сами правильные значения выхода. Обучение без учителя не требует знания правильных ответов на каждый пример обучающей выборки. В этом случае раскрывается внутренняя структура данных или корреляции между образцами в системе данных, что позволяет распределить образцы по категориям. При смешанном обучении часть весов определяется посредством обучения с учителем, в то время как остальная получается с помощью самообучения.
Теория обучения рассматривает три фундаментальных свойства, связанных с обучением по примерам: емкость, сложность образцов и вычислительная сложность. Под емкостью понимается, сколько образцов может запомнить сеть, и какие функции и границы принятия решений могут быть на ней сформированы. Сложность образцов определяет число обучающих примеров, необходимых для достижения способности сети к обобщению. Слишком малое число примеров может вызвать "переобученность" сети, когда она хорошо функционирует на примерах обучающей выборки, но плохо - на тестовых примерах, подчиненных тому же статистическому распределению. Известны 4 основных типа правил обучения: коррекция по ошибке, машина Больцмана, правило Хебба и обучение методом соревнования.
Правило коррекции по ошибке. При обучении с учителем для каждого входного примера задан желаемый выход d. Реальный выход сети y может не совпадать с желаемым. Принцип коррекции по ошибке при обучении состоит в использовании сигнала (d-y) для модификации весов, обеспечивающей постепенное уменьшение ошибки. Обучение имеет место только в случае, когда перцептрон ошибается. Известны различные модификации этого алгоритма обучения [2].
Обучение Больцмана. Представляет собой стохастическое правило обучения, которое следует из информационных теоретических и термодинамических принципов [10]. Целью обучения Больцмана является такая настройка весовых коэффициентов, при которой состояния видимых нейронов удовлетворяют желаемому распределению вероятностей. Обучение Больцмана может рассматриваться как специальный случай коррекции по ошибке, в котором под ошибкой понимается расхождение корреляций состояний в двух режимах .
Правило Хебба. Самым старым обучающим правилом является постулат обучения Хебба [13]. Хебб опирался на следующие нейрофизиологические наблюдения: если нейроны с обеих сторон синапса активизируются одновременно и регулярно, то сила синаптической связи возрастает. Важной особенностью этого правила является то, что изменение синаптического веса зависит только от активности нейронов, которые связаны данным синапсом. Это существенно упрощает цепи обучения в реализации VLSI.
Обучение методом соревнования. В отличие от обучения Хебба, в котором множество выходных нейронов могут возбуждаться одновременно, при соревновательном обучении выходные нейроны соревнуются между собой за активизацию. Это явление известно как правило "победитель берет все". Подобное обучение имеет место в биологических нейронных сетях. Обучение посредством соревнования позволяет кластеризовать входные данные: подобные примеры группируются сетью в соответствии с корреляциями и представляются одним элементом.
При обучении модифицируются только веса "победившего" нейрона. Эффект этого правила достигается за счет такого изменения сохраненного в сети образца (вектора весов связей победившего нейрона), при котором он становится чуть ближе ко входному примеру. На рис. 3 дана геометрическая иллюстрация обучения методом соревнования. Входные векторы нормализованы и представлены точками на поверхности сферы. Векторы весов для трех нейронов инициализированы случайными значениями. Их начальные и конечные значения после обучения отмечены Х на рис. 3а и 3б соответственно. Каждая из трех групп примеров обнаружена одним из выходных нейронов, чей весовой вектор настроился на центр тяжести обнаруженной группы.
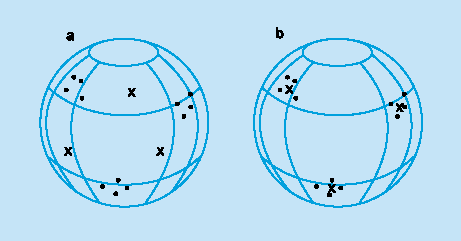
Рисунок 3.
Пример
обучения методом соревнования:
(а) перед обучением; (б) после обучения.
Можно заметить, что сеть никогда не перестанет обучаться, если параметр скорости обучения не равен 0. Некоторый входной образец может активизировать другой выходной нейрон на последующих итерациях в процессе обучения. Это ставит вопрос об устойчивости обучающей системы. Система считается устойчивой, если ни один из примеров обучающей выборки не изменяет своей принадлежности к категории после конечного числа итераций обучающего процесса. Один из способов достижения стабильности состоит в постепенном уменьшении до 0 параметра скорости обучения. Однако это искусственное торможение обучения вызывает другую проблему, называемую пластичностью и связанную со способностью к адаптации к новым данным. Эти особенности обучения методом соревнования известны под названием дилеммы стабильности-пластичности Гроссберга.
В Таблице 2 представлены различные алгоритмы обучения и связанные с ними архитектуры сетей (список не является исчерпывающим). В последней колонке перечислены задачи, для которых может быть применен каждый алгоритм. Каждый алгоритм обучения ориентирован на сеть определенной архитектуры и предназначен для ограниченного класса задач. Кроме рассмотренных, следует упомянуть некоторые другие алгоритмы: Adaline и Madaline [14], линейный дискриминантный анализ [15], проекции Саммона [15], анализ главных компонентов [2].
Таблица 2.
Известные
алгоритмы обучения.
|
Парадигма |
Обучающее правило |
Архитектура |
Алгоритм обучения |
Задача |
|
С учителем |
Коррекция ошибки |
Однослойный и многослойный перцептрон |
Алгоритмы обучения перцептрона |
Классификация образов |
|
Больцман |
Рекуррентная |
Алгоритм обучения Больцмана |
Классификация образов |
|
|
Хебб |
Многослойная прямого распространения |
Линейный дискриминантный анализ |
Анализ данных |
|
|
Соревнование |
Соревнование |
Векторное квантование |
Категоризация внутри класса Сжатие данных |
|
|
Сеть ART |
ARTMap |
Классификация образов |
||
|
Без учителя |
Коррекция ошибки |
Многослойная прямого распространения |
Проекция Саммона |
Категоризация внутри класса Анализ данных |
|
Хебб |
Прямого распространения или соревнование |
Анализ главных компонентов |
Анализ данных |
|
|
Сеть Хопфилда |
Обучение ассоциативной памяти |
Ассоциативная память |
||
|
Соревнование |
Соревнование |
Векторное квантование |
Категоризация |
|
|
SOM Кохонена |
SOM Кохонена |
Категоризация |
||
|
Сети ART |
ART1, ART2 |
Категоризация |
||
|
Смешанная |
Коррекция ошибки и соревнование |
Сеть RBF |
Алгоритм обучения RBF |
Классификация образов |
3. Многослойные сети прямого распространения
Стандартная L-слойная сеть прямого распространения состоит из слоя входных узлов (будем придерживаться утверждения, что он не включается в сеть в качестве самостоятельного слоя), (L-1) скрытых слоев и выходного слоя, соединенных последовательно в прямом направлении и не содержащих связей между элементами внутри слоя и обратных связей между слоями. На рис. 4 приведена структура трехслойной сети.
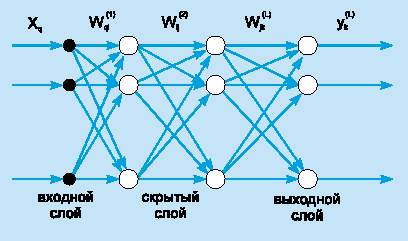
Рисунок 4.
Типовая
архитектура трехслойной сети прямого распространения.
3.1 Многослойный перцептрон
Наиболее популярный класс многослойных сетей прямого распространения образуют многослойные перцептроны, в которых каждый вычислительный элемент использует пороговую или сигмоидальную функцию активации. Многослойный перцептрон может формировать сколь угодно сложные границы принятия решения и реализовывать произвольные булевы функции [6]. Разработка алгоритма обратного распространения для определения весов в многослойном перцептроне сделала эти сети наиболее популярными у исследователей и пользователей нейронных сетей. Геометрическая интерпретация [14] объясняет роль элементов скрытых слоев (используется пороговая активационная функция).
3.2 RBF-сети
Сети, использующие радиальные базисные функции (RBF-сети), являются частным случаем двухслойной сети прямого распространения. Каждый элемент скрытого слоя использует в качестве активационной функции радиальную базисную функцию типа гауссовой. Радиальная базисная функция (функция ядра) центрируется в точке, которая определяется весовым вектором, связанным с нейроном. Как позиция, так и ширина функции ядра должны быть обучены по выборочным образцам. Обычно ядер гораздо меньше, чем обучающих примеров. Каждый выходной элемент вычисляет линейную комбинацию этих радиальных базисных функций. С точки зрения задачи аппроксимации скрытые элементы формируют совокупность функций, которые образуют базисную систему для представления входных примеров в построенном на ней пространстве.
Существуют различные алгоритмы обучения RBF-сетей [3]. Основной алгоритм использует двушаговую стратегию обучения, или смешанное обучение. Он оценивает позицию и ширину ядра с использованием алгоритма кластеризации "без учителя", а затем алгоритм минимизации среднеквадратической ошибки "с учителем" для определения весов связей между скрытым и выходным слоями. Поскольку выходные элементы линейны, применяется неитерационный алгоритм. После получения этого начального приближения используется градиентный спуск для уточнения параметров сети.
Этот смешанный алгоритм обучения RBF-сети сходится гораздо быстрее, чем алгоритм обратного распространения для обучения многослойных перцептронов. Однако RBF-сеть часто содержит слишком большое число скрытых элементов. Это влечет более медленное функционирование RBF-сети, чем многослойного перцептрона. Эффективность (ошибка в зависимости от размера сети) RBF-сети и многослойного перцептрона зависят от решаемой задачи.
3.3 Нерешенные проблемы
Существует множество спорных вопросов при проектировании сетей прямого распространения - например, сколько слоев необходимы для данной задачи, сколько следует выбрать элементов в каждом слое, как сеть будет реагировать на данные, не включенные в обучающую выборку (какова способность сети к обобщению), и какой размер обучающей выборки необходим для достижения "хорошей" способности сети к обобщению.
Хотя многослойные сети прямого распространения широко применяются для классификации и аппроксимации функций [2], многие параметры еще должны быть определены путем проб и ошибок. Существующие теоретические результаты дают лишь слабые ориентиры для выбора этих параметров в практических приложениях.
4. Самоорганизующиеся карты Кохонена
Самоорганизующиеся карты Кохонена (SOM) [16] обладают благоприятным свойством сохранения топологии, которое воспроизводит важный аспект карт признаков в коре головного мозга высокоорганизованных животных. В отображении с сохранением топологии близкие входные примеры возбуждают близкие выходные элементы. На рис. 2 показана основная архитектура сети SOM Кохонена. По существу она представляет собой двумерный массив элементов, причем каждый элемент связан со всеми n входными узлами.
Такая сеть является специальным случаем сети, обучающейся методом соревнования, в которой определяется пространственная окрестность для каждого выходного элемента. Локальная окрестность может быть квадратом, прямоугольником или окружностью. Начальный размер окрестности часто устанавливается в пределах от 1/2 до 2/3 размера сети и сокращается согласно определенному закону (например, по экспоненциально убывающей зависимости). Во время обучения модифицируются все веса, связанные с победителем и его соседними элементами.
Самоорганизующиеся карты Кохонена могут быть использованы для проектирования многомерных данных, аппроксимации плотности и кластеризации. Эта сеть успешно применялась для распознавания речи, обработки изображений, в робототехнике и в задачах управления [2]. Параметры сети включают в себя размерность массива нейронов, число нейронов в каждом измерении, форму окрестности, закон сжатия окрестности и скорость обучения.
5. Модели теории адаптивного резонанса
Напомним, что дилемма стабильности-пластичности является важной особенностью обучения методом соревнования. Как обучать новым явлениям (пластичность) и в то же время сохранить стабильность, чтобы существующие знания не были стерты или разрушены?
Карпентер и Гроссберг, разработавшие модели теории адаптивного резонанса (ART1, ART2 и ARTMAP) [17], сделали попытку решить эту дилемму. Сеть имеет достаточное число выходных элементов, но они не используются до тех пор, пока не возникнет в этом необходимость. Будем говорить, что элемент распределен (не распределен), если он используется (не используется). Обучающий алгоритм корректирует имеющийся прототип категории, только если входной вектор в достаточной степени ему подобен. В этом случае они резонируют. Степень подобия контролируется параметром сходства k, 0<k<1, который связан также с числом категорий. Когда входной вектор недостаточно подобен ни одному существующему прототипу сети, создается новая категория, и с ней связывается нераспределенный элемент со входным вектором в качестве начального значения прототипа. Если не находится нераспределенного элемента, то новый вектор не вызывает реакции сети.
Чтобы проиллюстрировать модель, рассмотрим сеть ART1, которая рассчитана на бинарный (0/1) вход. Упрощенная схема архитектуры ART1 [2] представлена на рис. 5. Она содержит два слоя элементов с полными связями.
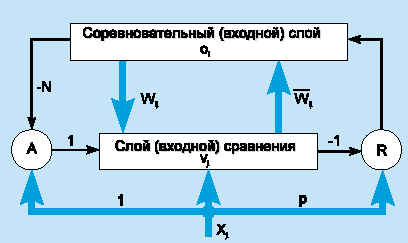
Рисунок 5.
Сеть
ART1.
Направленный сверху вниз весовой вектор wj соответствует элементу j входного слоя, а направленный снизу вверх весовой вектор i связан с выходным элементом i; i является нормализованной версией wi . Векторы wj сохраняют прототипы кластеров. Роль нормализации состоит в том, чтобы предотвратить доминирование векторов с большой длиной над векторами с малой длиной. Сигнал сброса R генерируется только тогда, когда подобие ниже заданного уровня.
Модель ART1 может создать новые категории и отбросить входные примеры, когда сеть исчерпала свою емкость. Однако число обнаруженных сетью категорий чувствительно к параметру сходства.
6. Сеть Хопфилда
Хопфилд использовал функцию энергии как инструмент для построения рекуррентных сетей и для понимания их динамики [7]. Формализация Хопфилда сделала ясным принцип хранения информации как динамически устойчивых аттракторов и популяризовала использование рекуррентных сетей для ассоциативной памяти и для решения комбинаторных задач оптимизации.
Динамическое изменение состояний сети может быть выполнено по крайней мере двумя способами: синхронно и асинхронно. В первом случае все элементы модифицируются одновременно на каждом временном шаге, во втором - в каждый момент времени выбирается и подвергается обработке один элемент. Этот элемент может выбираться случайно. Главное свойство энергетической функции состоит в том, что в процессе эволюции состояний сети согласно уравнению она уменьшается и достигает локального минимума (аттрактора), в котором она сохраняет постоянную энергию.
6.1 Ассоциативная память
Если хранимые в сети образцы являются аттракторами, она может использоваться как ассоциативная память. Любой пример, находящийся в области притяжения хранимого образца, может быть использован как указатель для его восстановления.
Ассоциативная память обычно работает в двух режимах: хранения и восстановления. В режиме хранения веса связей в сети определяются так, чтобы аттракторы запомнили набор p n-мерных образцов {x1, x2,..., xp), которые должны быть сохранены. Во втором режиме входной пример используется как начальное состояние сети, и далее сеть эволюционирует согласно своей динамике. Выходной образец устанавливается, когда сеть достигает равновесия.
Сколько примеров могут быть сохранены в сети с n бинарными элементами? Другими словами, какова емкость памяти сети? Она конечна, так как сеть с n бинарными элементами имеет максимально 2n различных состояний, и не все из них являются аттракторами. Более того, не все аттракторы могут хранить полезные образцы. Ложные аттракторы могут также хранить образцы, но они отличаются от примеров обучающей выборки. Показано, что максимальное число случайных образцов, которые может хранить сеть Хопфилда, составляет Pmax ( 0.15 n. Когда число сохраняемых образцов p ( 0.15 n, достигается наиболее успешный вызов данных из памяти. Если запоминаемые образцы представлены ортогональными векторами (в отличие от случайных), то количество сохраненных в памяти образцов будет увеличиваться. Число ложных аттракторов возрастает, когда p достигает емкости сети. Несколько правил обучения предложено для увеличения емкости памяти сети Хопфилда [2]. Заметим, что в сети для хранения p n-битных примеров требуется реализовать 2n связей.
6.2 Минимизация энергии
Сеть Хопфилда эволюционирует в направлении уменьшения своей энергии. Это позволяет решать комбинаторные задачи оптимизации, если они могут быть сформулированы как задачи минимизации энергии. В частности, подобным способом может быть сформулирована задача коммивояжера.
7. Приложения
В начале статьи были описаны 7 классов различных приложений ИНС. Следует иметь в виду, что для успешного решения реальных задач необходимо определить ряд характеристик, включая модель сети, ее размер, функцию активации, параметры обучения и набор обучающих примеров. Для иллюстрации практического применения сетей прямого распространения рассмотрим проблему распознавания изображений символов (задача OCR, которая состоит в обработке отсканированного изображения текста и его преобразовании в текстовую форму).
7.1 Система OCR
Система OCR обычно состоит из блоков препроцессирования, сегментации, выделения характеристик, классификации и контекстуальной обработки. Бумажный документ сканируется, и создается изображение в оттенках серого цвета или бинарное (черно-белое) изображение. На стадии препроцессирования применяется фильтрация для удаления шума, область текста локализуется и преобразуется к бинарному изображению с помощью глобального и локального адаптивного порогового преобразователя. На шаге сегментации изображение текста разделяется на отдельные символы. Эта задача особенно трудна для рукописного текста, который содержит связи между соседними символами. Один из эффективных приемов состоит в расчленении составного образца на малые образцы (промежуточная сегментация) и нахождении точек правильной сегментации с использованием выхода классификатора по образцам. Вследствие различного наклона, искажений, помех и стилей письма распознавание сегментированных символов является непростой задачей.
7.2 Схемы вычислений
На рис. 6 представлены две основные схемы использования ИНС в OCR системах. Первая выполняет явное извлечение характерных признаков (не обязательно на нейронной сети). Например, это могут быть признаки обхода по контуру. Выделенные признаки подаются на вход многослойной сети прямого распространения [19]. Эта схема отличается гибкостью в отношении использования большого разнообразия признаков. Другая схема не предусматривает явного выделения признаков из исходных данных. Извлечение признаков происходит неявно в скрытых слоях ИНС. Удобство этой схемы состоит в том, что выделение признаков и классификация объединены и обучение происходит одновременно, что дает оптимальный результат классификации. Однако схема требует большего размера сети, чем в первом случае.
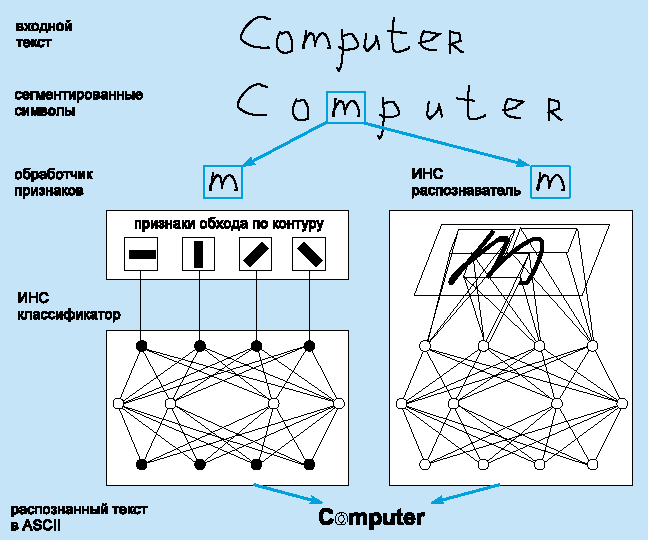
Рисунок 6.
Две
схемы применения ИНС в системах OCR.
Типичный пример подобной интегрированной схемы рассмотрен Куном [20] для распознавания zip-кода.
7.3 Результаты
ИНС очень эффективно применяются в OCR-приложениях. Однако, нет убедительных доказательств их превосходства над соответствующими статистическими классификаторами. На первой конференции по OCR-системам в 1992 г. [18] более 40 систем распознавания рукописного текста были сопоставлены для одних и тех же данных. Из них 10 лучших использовали вариант многослойной сети прямого распространения или классификатор "ближайшего соседа". ИНС имеют тенденцию к превосходству по скорости и требуемой памяти по сравнению с методом "ближайшего соседа", в отличие от которого скорость классификации с применением ИНС не зависит от объема обучающей выборки. Точность распознавания лучших OCR-систем на базе данных предварительно сегментированных символов составила около 98% для цифр, 96% для заглавных букв и 87 - для строчных. (Низкая точность для строчных букв вызвана в значительной степени тем, что тестовые данные существенно отличались от тренировочных.) По данным теста можно сделать вывод, что на изолированных символах OCR система близка по точности к человеку. Однако человек опережает системы OCR на свободных от ограничений и рукописных документах.
Заключение
Развитие ИНС вызвало немало энтузиазма и критики. Некоторые сравнительные исследования оказались оптимистичными, другие - пессимистичными. Для многих задач, таких как распознавание образов, пока не создано доминирующих подходов. Выбор лучшей технологии должен диктоваться природой задачи. Нужно пытаться понять возможности, предпосылки и область применения различных подходов и максимально использовать их дополнительные преимущества для дальнейшего развития интеллектуальных систем. Подобные усилия могут привести к синергетическому подходу, который объединяет ИНС с другими технологиями для существенного прорыва в решении актуальных проблем. Как недавно заметил Минский, пришло время строить системы за рамками отдельных компонентов. Индивидуальные модули важны, но мы также нуждаемся в методологии интеграции. Ясно, что взаимодействие и совместные работы исследователей в области ИНС и других дисциплин позволят не только избежать повторений, но и (что более важно) стимулируют и придают новые качества развитию отдельных направлений.
Литература
[1] DARPA Neural Network Study, AFCEA Int'l Press, Fairfax, Va., 1988.
[2] J. Hertz, A. Krogh, and R.G. Palmer, Introduction to the Theory of Neural Computation, Addison-Wesley, Reading, Mass., 1991.
[3] S. Haykin, Neural Networks: A Comprehensive Foundation, MacMillan College Publishing Co., New York, 1994.
[4] W.S. McCulloch and W. Pitts, "A logical Calculus of Ideas Immanent in Nervous Activity", Bull. Mathematical Biophysics, Vol. 5, 1943, pp. 115-133.
[5] R.Rosenblatt, "Principles of Neurodynamics", Spartan Books, New York, 1962.
[6] M. Miтnsky and S. Papert, "Perceptrons: An Introduction to Computational Geometry", MIT Press, Cambridge, Mass., 1969.
[7] J.J. Hopfield, "Neural Networks and Physical Systems with Emergent Collective Computational Abilities", in Proc. National Academy of Sciencies, USA 79, 1982, pp. 2554-2558.
[8] P. Werbos, "Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences", Phd Thesis, Dept. of Applied Mathematics, Harvard University, Cambridge, Mass., 1974.
[9] D.E. Rumelhart and J.L. McClelland, Parallel Distributed Processing: Exploration in the Microstructure of Cognition, MIT Press, Cambridge, Mass., 1986.
[10] J.A. Anderson and E. Rosenfeld, "Neurocomputing: Foundation of Research", MIT Press, Cambridge, Mass., 1988.
[11] S. Brunak and B. Lautrup, Neural Networks, Computers with Intuition, World Scientific, Singapore, 1990.
[12] J. Feldman, M.A. Fanty, and N.H. Goddard, "Computing with Structured Neural Networks", Computer, Vol. 21, No. 3, Mar.1988, pp. 91-103.
[13] D.O. Hebb, The Organization of Behavior, John Wiley & Sons, New York, 1949.
[14] R.P.Lippmann, "An Introduction to Computing with Neural Nets", IEEE ASSP Magazine, Vol.4, No.2, Apr. 1987, pp. 4-22.
[15] A.K. Jain and J. Mao, "Neural Networks and Pattern Recognition", in Computational Intelligence: Imitating Life, J.M. Zurada, R.J. Marks II, and C.J. Robinson, eds., IEEE Press, Piscataway, N.J., 1994, pp. 194-212.
[16] T. Kohonen, SelfOrganization and Associative Memory, Third Edition, Springer-Verlag, New York, 1989.
[17] G.A.Carpenter and S. Grossberg, Pattern Recognition by SelfOrganizing Neural Networks, MIT Press, Cambridge, Mass., 1991.
[18] "The First Census Optical Character Recognition System Conference", R.A.Wilkinson et al., eds., . Tech. Report, NISTIR 4912, US Deop. Commerse, NIST, Gaithersburg, Md., 1992.
[19] K. Mohiuddin and J. Mao, "A Comparative Study of Different Classifiers for Handprinted Character Recognition", in Pattern Recognition in Practice IV, E.S. Gelsema and L.N. Kanal, eds., Elsevier Science, The Netherlands, 1994, pp. 437-448.
[20] Y.Le Cun et al., "Back-Propagation Applied to Handwritten Zip Code Recognition", Neural Computation, Vol 1, 1989, pp. 541-551.
[21] M. Minsky, "Logical Versus Analogical or Symbolic Versus Connectionist or Neat Versus Scruffy", AI Magazine, Vol. 65, No. 2, 1991, pp. 34-51.
