Сети эхо-состояний (ESN) обеспечивают архитектуру и контролируемый принцип обучения для рекуррентных нейронных сетей (RNN). Основная идея заключается в том, чтобы (i) управлять случайной, большой, фиксированной рекуррентной нейронной сетью с помощью входного сигнала, тем самым вызывая у каждого нейрона в этой "резервной" сети нелинейный ответный сигнал, и (ii) комбинировать желаемый выходной сигнал с помощью обучаемой линейной комбинации всех этих ответных сигналов.

Основная идея ESNs перекликается с Liquid State Machines (LSM), которые были разработаны Вольфгангом Маассом независимо от ESNs и одновременно с ними (Maass W., Natschlaeger T., Markram H., 2002). Все чаще LSM, ESN и недавно изученное правило изучения декорреляции обратного распространения для RNN (Schiller and Steil, 2005) объединяются под названием "Вычисления коллектора". Шиллер и Стайл (Schiller and Steil, 2005) также показали, что в традиционных методах тренировки для RNN, при которых адаптируются все веса (а не только выходные), основные изменения происходят в выходных весах. В области когнитивной нейронауки аналогичный механизм был исследован Питером Ф. Домини в контексте моделирования обработки последовательностей в мозге млекопитающих, особенно распознавания речи в мозге человека (например, Dominey 1995, Dominey, Hoen and Inui 2006). Основная идея также легла в основу модели временного распознавания входных данных в биологических нейронных сетях (Буономано и Мерцених, 1995). Ранняя четкая формулировка идеи вычисления резервуара принадлежит К. Кирби, который раскрыл эту концепцию в почти забытом (1 ссылка на Google по состоянию на 2017 год) материале конференции (Kirby, 1991). Самая ранняя из известных на сегодняшний день формулировок идеи вычисления резервуара была дана Л. Шомейкером (1990 [= глава 7 в Schomaker 1991], 1992), который описал, как можно получить желаемый целевой результат от RNN, научившись комбинировать сигналы от случайно сконфигурированного ансамбля импульсных нейронных генераторов.

В качестве иллюстрации рассмотрим задачу обучения RNN вести себя как генератор настраиваемой частоты (загрузите код MATLAB из этого примера). Входной сигнал u(n) представляет собой медленно изменяющуюся настройку частоты, желаемый выходной сигнал y(n) представляет собой синусоиду частоты, указанной текущим входным сигналом. Предположим, что задана обучающая последовательность ввода-вывода D=(u(1),y(1)),...,(u(nmax),y(nmax)) (см. Входные и выходные сигналы в ; здесь входные данные представляют собой медленную случайную ступенчатую функцию, указывающую частоты в диапазоне от 1/16 до 1/4 Гц). Задача состоит в том, чтобы обучить RNN на основе этих обучающих данных таким образом, чтобы при медленном тестировании входных сигналов на выходе снова была синусоидальная частота, определенная на входе.

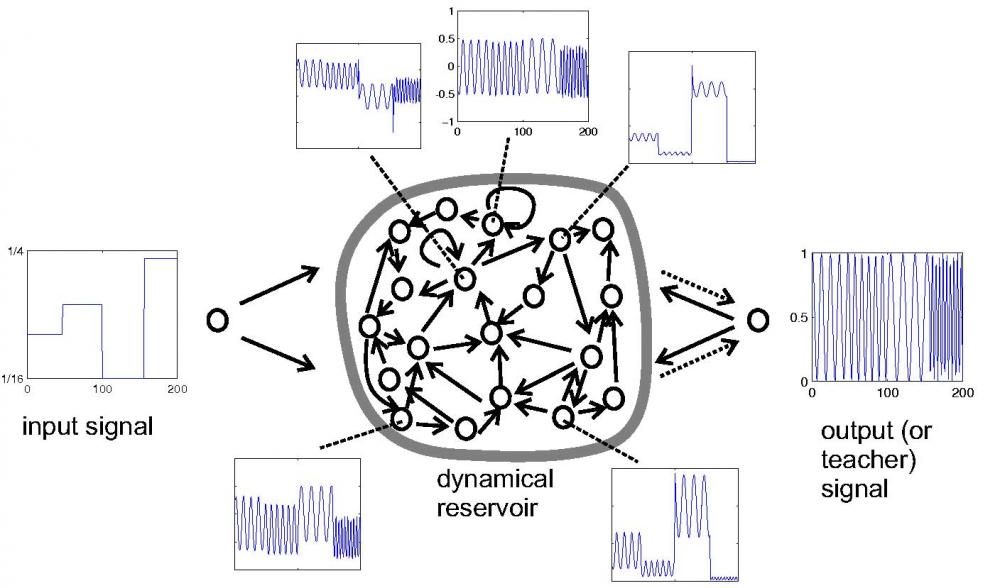
Шаг 1: Задайте случайный RNN. (i) Создайте случайный динамический RNN резервуара, используя любую модель нейрона (в демонстрационном примере с генератором частоты использовались нейроны-интеграторы без всплесков). Размер резервуара N зависит от задачи. В демонстрационном задании с генератором частоты использовалось N=200. (ii) Подключите входные блоки к резервуару, создав произвольные соединения "все ко всем". (iii) Создайте выходные блоки. Если для задачи требуется обратная связь по выходу (как для задачи с генератором частоты), установите случайно сгенерированные соединения выход-резервуар ("все-ко-всему"). Если задача не требует обратной связи по выходу, не создавайте никаких подключений к блокам вывода на этом шаге.
Шаг 2: Собираем данные о состоянии резервуара. Управляйте динамическим резервуаром с помощью обучающих данных D в течение времени n=1,...,nmax . В демонстрационном примере, где имеются соединения с обратной связью "выход-резервуар", это означает запись как входных данных u(n) в блок ввода, так и выходных данных y(n) преподавателя в блок вывода ("принуждение преподавателя"). В задачах без обратной связи по выходу резервуар управляется только входным сигналом u(n). В результате получается последовательность x(n) N-мерных состояний резервуара. Каждый составляющий сигнал x(n) является нелинейным преобразованием управляющего входного сигнала. В демонстрационной версии каждый x (n) представляет собой индивидуальную смесь входного сигнала с медленным шагом и быстрой выходной синусоидальной волны (см. Пять примерных графиков состояния нейронов на рисунке 1).
Шаг 3: Вычислите выходные веса. Вычислите выходные значения как значения линейной регрессии выходных данных y(n) преподавателя для состояний хранилища x(n). Используйте эти значения для создания связей между хранилищем и выходом (пунктирные стрелки на рисунке 1). На этом обучение завершено, и ESN готов к использованию. На рисунке 2 показан выходной сигнал, полученный при подключении обученного ESN к входу с медленным шагом, показанному на том же рисунке.

Сети эхо-состояний могут быть созданы с прямыми обучаемыми соединениями ввода-вывода или без них, с обратной связью вывода-хранилища или без нее, с различными типами нейронов, различными схемами подключения к внутреннему резервуару и т.д. Кроме того, выходные веса могут быть вычислены с помощью любого из доступных автономных или онлайн-алгоритмов линейной регрессии. Помимо решений с наименьшей среднеквадратичной ошибкой (т.е. весов линейной регрессии), для определения выходных весов использовались критерии максимизации запаса, известные из методов обучения опорным векторам (Schmidhuber et al., 2007).

Объединяющей темой всех этих вариаций является использование фиксированного RNN в качестве случайной нелинейной возбудимой среды, чей многомерный динамический "эхо-отклик" на управляющий входной сигнал (и/или выходную обратную связь) используется в качестве неортогональной сигнальной основы для восстановления желаемого выходного сигнала с помощью линейной комбинации, минимизирующей некоторые критерии ошибки.

Формализм и теория
Системные уравнения. Базовая сигмовидная эхо-сеть с дискретным временем, состоящая из N единиц хранения, K входов и L выходов, определяется уравнением обновления состояния

(1) x(n+1)=f(Wx(n)+Winu(n+1)+Wfby(n)) ,

где x(n) - N-мерное состояние резервуара, f - сигмоидальная функция (обычно логистическая сигмоида или функция tanh), W - матрица веса резервуара N× N, Win - входная матрица веса N×K, u(n) - K-мерный входной сигнал, Wfb это выходная матрица обратной связи N× L, а y(n) - L-мерный выходной сигнал. В задачах, где обратная связь на выходе не требуется, Wfb обнуляется. Расширенное состояние системы z(n)=[x(n);u(n)] в момент времени n представляет собой объединение состояний резервуара и входных данных. Выходные данные получены из расширенного состояния системы по формуле

(2) y(n)=g(Woutz(n)) ,

где g - выходная функция активации (обычно единичная или сигмовидная), а Wout - L× (K +N)-мерная матрица выходных весов.

Обучающие уравнения. На этапе сбора данных о состоянии ESN управляется входной последовательностью u(1),...,u(nmax), которая выдает последовательность z(1),...,z(nmax) расширенных состояний системы. Здесь используются системные уравнения (1), (2). Если модель включает обратную связь по выходу (т.е. ненулевой Wfb), то во время генерации состояний системы правильные выходные данные d(n) (часть обучающих данных) записываются в выходные единицы ("принуждение учителя"). Полученные расширенные системные состояния записываются по строкам в матрицу S сбора данных о состояниях размером nmax×(N+K). Обычно некоторая начальная часть собранных таким образом состояний отбрасывается, чтобы обеспечить размыв произвольного (случайного или нулевого) исходного состояния хранилища, необходимого в момент времени 1. Аналогично, требуемые выходные данные d(n) сортируются по строкам в матрицу сбора выходных данных для учителя D размером nmax×L .

Требуемые выходные значения Wout - это веса линейной регрессии для желаемых выходных данных d(n) в собранных расширенных состояниях z(n). Математически простой способ вычисления Wout - вызвать псевдообратную (обозначаемую ⋅†) из S :

(3) Wout=(S†D)' ,

который является автономным алгоритмом (простое число обозначает транспонирование матрицы). Адаптивные методы, известные из линейной обработки сигналов, также могут быть использованы для вычисления выходных весов (Jaeger, 2003).

Свойство состояния эхо-сигнала. Для того чтобы принцип ESN работал, резервуар должен обладать свойством состояния эхо-сигнала (ESP), которое связывает асимптотические свойства динамики возбужденного резервуара с управляющим сигналом. Интуитивно понятно, что ESP утверждает, что резервуар асимптотически удалит любую информацию из начальных условий. ESP гарантирован для резервуаров с аддитивными сигмовидными нейронами, если матрица веса резервуара (и скорости утечки) удовлетворяет определенным алгебраическим условиям в терминах сингулярных значений. Для таких резервуаров с сигмовидной формой tanh ESP нарушается при нулевом вводе, если спектральный радиус матрицы веса резервуара больше единицы. И наоборот, эмпирически установлено, что ESP предоставляется для любого входного сигнала, если этот спектральный радиус меньше единицы. В литературе это привело к распространенному, но ошибочному определению ESP со спектральным радиусом менее 1. В частности, чем больше амплитуда входного сигнала, тем больше может быть спектральный радиус, превышающий единицу, при сохранении ESP. Абстрактная характеристика ESP для произвольных типов резервуаров и алгебраические условия для резервуаров аддитивных сигмовидных нейронов приведены в Jaeger (2001a); для важного подкласса резервуаров более жесткие алгебраические условия приведены в Buehner and Young (2006) и Yildiz et al. (2012); для нейронов с протекающими интеграторами., алгебраические условия изложены в Jaeger et al. (2007). Взаимосвязь между характеристиками входного сигнала и ESP исследована в работах Манджуната и Джегера (2013), где показан фундаментальный закон 0-1: если вход поступает от стационарного источника, ESP выполняется с вероятностью 1 или 0.

Объем памяти. Из-за того, что RNNS поддерживает автоматическую обратную связь, состояния хранилища x(n) отражают следы прошлой истории ввода. Это можно рассматривать как динамическую кратковременную память. Для ESN с одним входом объем C этой кратковременной памяти может быть количественно определен как C=∑i=1,2,...r2(u(n-i),yi(n)) , где r2(u(n-i),yi(n)) − квадрат коэффициент корреляции между входным сигналом, задержанным на i, и обученным выходным сигналом yi(n), который был обучен заданию ретродиктировать (запоминать) u(n−i) по входному сигналу u(n). Получается, что для i.i.d. при вводе данных объем памяти C сети эхо-состояний размера N ограничен значением N; при отсутствии числовых ошибок и линейном накопителе достигается ограничение (Jaeger 2002a; White and Sompolinsky 2004; Hermans & Schrauwen 2009). Эти результаты означают, что невозможно обучить ESN задачам, требующим неограниченного объема памяти, таким как, например, задачи контекстно-свободного разбора грамматики (Schmidhuber et al., 2007). Однако, если выходные блоки с обратной связью с резервуаром обучаются как блоки памяти аттрактора, неограниченные объемы памяти могут быть реализованы и с помощью ESN (см. пример мультистабильного переключения в Jaeger 2002a; основы теории аттракторов удержания в памяти, вызванных обратной связью, в Maass, Joshi & Sontag 2007; модель рабочей памяти со стабильными состояниями аттрактора на основе ESN в Pascanu & Jaeger 2010).

Универсальные вычислительные и аппроксимирующие свойства. ESNS может реализовать любой нелинейный фильтр с ограниченной памятью сколь угодно хорошо. Это направление теоретических исследований было начато и продвинуто в области автоматов с конечным состоянием (Maass, Natschlaeger & Markram, 2002; Maass, Joshi & Sontag, 2007), и читатель может ознакомиться с подробностями в статье LSM.

Практические вопросы: настройка глобального контроля и регуляризация
При использовании ESNS в практических задачах нелинейного моделирования конечной целью является минимизация ошибки тестирования. Стандартный метод машинного обучения для получения оценки ошибки тестирования заключается в использовании только части доступных обучающих данных для оценки модели и мониторинге производительности модели на основе утаенной части исходных обучающих данных (набора для проверки). Вопрос в том, как можно оптимизировать модели ESN, чтобы уменьшить количество ошибок в наборе проверки? В терминологии машинного обучения это сводится к вопросу о том, как можно снабдить модели ESN смещением, соответствующим задаче. В ESNS существует три вида смещения (в широком смысле), которые следует корректировать.

Первый вид смещения заключается в использовании регуляризации. По сути, это означает, что модели сглаживаются. Два стандартных способа добиться некоторого сглаживания заключаются в следующем:

Регрессия гребня (также известная как регуляризация по Тихонову): измените уравнение линейной регрессии (3) для выходных весов.:
(4) Wout=(R+a2I)−1P ,
где R=1/nmaxS - матрица корреляции состояний расширенного резервуара, P=1/Nmaxs'D - матрица взаимной корреляции состояний по сравнению с желаемые выходные данные, α2 - это некоторое неотрицательное число (чем больше, тем сильнее эффект сглаживания), а I - единичная матрица.

Шум состояния: Во время сбора данных о состоянии вместо (1) используйте обновление состояния, которое добавляет вектор шума ν(n) к состояниям хранилища.:
(5) x(n+1)=f(Wx(n)+Winu(n+1)+Wfby(n))+ν(n) .
Оба метода приводят к уменьшению выходного веса. Добавление шума состояния требует больших вычислительных затрат, но, по-видимому, дает дополнительное преимущество в виде стабилизации решений в моделях с обратной связью по выходу (Jaeger 2002a; Jaeger, Lukosevicius, Popovici & Siewert 2007).

Второй вид смещения достигается за счет создания сети эхо-состояний, как можно было бы сказать, "динамически подобной" системе, которую вы хотите смоделировать. Например, если исходная система развивается медленно, ESN должна делать то же самое; или если исходная система имеет большой объем памяти, то и ESN должна делать то же самое. Такое формирование основных динамических характеристик осуществляется путем настройки небольшого числа глобальных управляющих параметров:

Спектральный радиус матрицы веса резервуара определяет (i) эффективную постоянную времени сети эхо-сигналов (больший спектральный радиус подразумевает более медленное затухание импульсной характеристики) и (ii) степень нелинейного взаимодействия входных компонентов во времени (больший спектральный радиус подразумевает взаимодействие на большем расстоянии).
Входной масштабирующий код определяет степень нелинейности динамики коллектора. С одной стороны, при очень малых эффективных входных амплитудах резервуар ведет себя почти как линейная среда, в то время как с другой стороны, очень большие входные амплитуды приводят к насыщению нейронов сигмовидной кишки, что приводит к бинарной динамике переключения.
Масштабирование выходной обратной связи определяет степень, в которой обученный ESN обладает автономным компонентом генерации шаблонов. ESN без какой-либо выходной обратной связи являются типичным выбором для задач распознавания и классификации динамических образов, управляемых исключительно входными данными. С другой стороны, для демонстрации работы генератора частоты требовалась сильная обратная связь на выходе, чтобы генерировать колебания (которых нет на входе). Ненулевая обратная связь на выходе создает опасность динамической нестабильности.
Часто утверждается (начиная с ранних технических отчетов Jaeger), что связность матрицы весов коллектора отвечает за "богатство" сигналов отклика в коллекторе, следуя следующей логике: разреженная связность → разложение динамики коллектора на слабо связанные подсистемы → большие различия между сигналами коллектора (желательно). Однако, вопреки этой интуиции, многие авторы сообщают, что полностью подключенные резервуары работают так же хорошо, как и слабо подключенные. Учитывая, что сети с редким, но случайным подключением обладают свойствами малого мира, представляется вероятным, что редкое случайное подключение не приводит к динамическому разъединению, поэтому первоначальные интуитивные предположения ошибочны. Более важным с практической точки зрения аспектом разреженной связности является то, что она приводит к линейному масштабированию вычислительной сложности. Если хранилища настроены таким образом, что каждый нейрон в среднем подключается к фиксированному числу K других нейронов, независимо от размера сети N, вычислительные затраты на запуск обученных сетей растут только линейно с увеличением N.

Наконец, третий вид смещения (здесь терминология немного расширена) - это просто размер хранилища N . В смысле теории статистического обучения увеличение размера хранилища является наиболее прямым способом увеличения производительности модели.

Все эти виды смещения должны быть оптимизированы совместно. В настоящее время стандартной практикой для этого является экспериментирование вручную. Практические "приемы работы" собраны в книге Лукошявичюса (2012).

Значимость
С начала 1990-х годов известен ряд алгоритмов для контролируемого обучения RNN, в первую очередь рекуррентное обучение в реальном времени (Уильямс и Ципсер, 1989), обратное распространение во времени (Вербос, 1990), методы, основанные на расширенной фильтрации Калмана (Пускориус и Фельдкамп, 2004), и алгоритм Атия-Парлоса (Atiya-Parlos). и Parlos 2000). Все эти алгоритмы адаптируют все соединения (входные, рекуррентные, выходные) с помощью той или иной версии градиентного спуска. Это делает эти алгоритмы медленными и, что, возможно, еще более громоздкими, приводит к нарушению процесса обучения из-за бифуркаций (Doya 1992); сходимость не может быть гарантирована. Как следствие, RNN редко использовались в практических инженерных приложениях в то время, когда были внедрены ESN. Обучение с помощью ESN, напротив, происходит быстро, не имеет сбоев и легко реализуется. В ряде контрольных задач ESNS значительно превзошли все другие методы нелинейного динамического моделирования (Jaeger and Haas, 2004, Jaeger et al., 2007).

Сегодня (по состоянию на 2017 год), с появлением глубокого обучения, проблемы, с которыми сталкивается обучение рекуррентных нейронных сетей на основе градиентного спуска, можно считать решенными. Первоначальная уникальная особенность ESNS - стабильные и простые алгоритмы обучения - исчезла. Более того, методы глубокого обучения для RNNS доказали свою эффективность при решении очень сложных задач моделирования, особенно в области языка и обработки речи. Для достижения подобных уровней сложности потребовались бы хранилища непомерного размера. Методы расчета запасов, тем не менее, являются альтернативой, которую стоит рассмотреть, когда моделируемая система не слишком сложна и когда требуется дешевое, быстрое и адаптивное обучение. Это справедливо для многих применений в обработке сигналов, таких как, например, обработка биосигналов (Kudithipudi et al., 2015), дистанционное зондирование (Antonelo, 2017) или управление двигателями роботов (Polydoros et al., 2015).

Примерно с 2010 года сети эхо-состояний стали актуальными и довольно популярными в качестве вычислительного принципа, который хорошо сочетается с нецифровыми вычислительными субстратами, такими как оптические микрочипы (Вандорн и др., 2014), механические наногенераторы (Куломб, Йорк и Сильвестр, 2017), нейроморфные микрочипы на основе мемристоров (Бюргер и др., 2017). 2015), смеси углеродных нанотрубок и полимеров (Dale et al., 2016) или даже искусственные мягкие конечности (Nakajima, Hauser and Pfeifer, 2015). Таким нестандартным вычислительным материалам и изготовленным из них микроустройствам часто не хватает точности вычислений, они демонстрируют значительное несоответствие между устройствами, а способы эмуляции классических логических схем переключения неизвестны. Но часто нелинейную динамику можно выявить из соответствующим образом взаимосвязанных ансамблей таких элементов, то есть можно создать физические хранилища, что открывает возможности для обучения таких систем с помощью методов ESN.