Байесовская ловушка
Байесовская ловушка
https://science.d3.ru/baiesovskaia-lovushka-1366880/?sorting=rating
Этот пост, пожалуй, можно было бы выложить и на политоту, или даже на политикс. Хороший повод задуматься о том, как мы попадаем в плен собственных иллюзий и становимся жертвой "самосбывающихся пророчеств".
Написалsyd6 мая 2017 в 18:01
192
5949
все комментарии (48)
только новые
Комментировать
Сразу кину камень в
переводчиков: он Байес, с ударением
на первом слоге. Теперь по сути.
Чувак на видео затронул очень интересную тему. Мы действительно очень плохо
умеем рассчитыватьбайесовскую вероятность, но при этом мы очень
хорошо умеем ее интуитивно использовать. Может быть это для кого–то
будет открытием, но вычисления не являются для людей чем–то естественным и
интуитивно понятным, считать мы учимся. А вот интуитивно оценивать вероятности
было очень важно для выживания.
Вчера удачно сорвал банан с дерева, и тигра рядом не видел, и тигр сейчас
должен быть сыт, поскольку съел антилопу — значит можно идти за следующим
бананом. Само по себе ни одно из событий не дает уверенности в безопасности
данного предприятия, но все они вместе дают почти полную уверенность.
Заинтересовавшимся можно дать несколько советов. Как бы от гуру, а на самом
деле следующих из байесовской логики.
— никогда не верьте во что угодно на 100%
— никогда не отрицайте что угодно на 100%
— время от времени изменяйте своим привычкам.
— не бойтесь менять убеждения
79
НаписалDedushka_shubin6 мая 2017 в 19:37ответить
Dedushka_shubin, Ага, я прям ждал, когда он до черных лебедей дойдет. Ну вот какой опыт человечества, обновляемый по Байесу, мог предсказать вероятность того, что террористы захватят два самолета и направят их в башни? Или вот что чувак, который начал как обычный гринмейлер корпораций, потеряет глаз от зеленки?
-1
Написалptitzin6 мая 2017 в 20:25ответить
ptitzin, но ведь не дошел же. И правильно сделал. Потому что черные лебеди — из другого заповедника.
0
НаписалDedushka_shubin6 мая 2017 в 22:30ответить
Dedushka_shubin, ну не знаю. Я учился на прикладного математика, финансовая статистика и бросил это именно из–за черных лебедей. Портфели балансировать это не интересно, продавать бумаги, на которые ткнул начальник, тоже, а вот случайность и хаос — это завораживает. Поэтому я и рисую — в этом достаточно много случайности.
5
Написалptitzin7 мая 2017 в 08:46ответить
ptitzin, есть подозрение, что бросили вы потому–что склонны больше к рисованию, чем к расчётам.
3
Написалyukkatan12 мая 2017 в 13:00ответить
yukkatan, Ну как–то так выяснил, что могу, но не радует. Склонность к рисованию я целенаправленно в себе воспитывал. Еще так же я выяснил, что не склонен к написанию музыки и к работе на сцене. А так же к администрированию сетей.
0
Написалptitzin12 мая 2017 в 13:06ответить
ptitzin, а у вас случайно не было изначально влечения к программированию, которое после фиаско из–за проблем с объектно–ориентированным моделированием трансформировалось в администрирование сетей?
0
Написалyukkatan12 мая 2017 в 13:27ответить
yukkatan, нет, не было. Я проверял
0
Написалptitzin12 мая 2017 в 13:58ответить
ptitzin,
Хуево Вы на математика учились. Лебеди — это вовсе не функция апдейта, а
исходной степени веры. Скажем если мы определяем параметр биномиального
распределения с неизвестной вероятностью события p, то для неиформативного
prior мы используем гамму с альфа, бета=1.
Другими словами, мы изначально предполагаем что у монеты в принципе может быть
две стороны даже если мы ее не видели вообще. Аналогично, для мультиномиального
распределения иэмы можем использовать Дирихле с начальными альфа=1 и тд и тп.
0
Написалvolkot13 мая 2017 в 01:42ответить
Dedushka_shubin, сколь помню, байесовская вероятность как раз контринтуитивна, в том числе и в "прикидках на глаз". Или я не правильно понял разницу между "рассчитывать" и "использовать"?
-1
НаписалSkyRzn6 мая 2017 в 23:55ответить
SkyRzn, видимо, вы неправильно
поняли слово "интуитивно". Допустим, есть такая проблема:
сосед–алкоголик 5 раз подряд занимал тыщу до зарплаты и ни разу не отдал. Надо
ему верить еще раз? Большинство людей скажет, что нет, не надо. Хотя формальная
логика говорит, что мы не можем быть уверены, что и в шестой раз он не вернет
деньги. Здесь интуитивная оценка работает. Теперь представьте ту же ситуацию
чуть иначе: некий филантроп говорит, что надо людям верить и готов
перестраховать долг соседа. Вам надо только оценить вероятность того, что он
все–таки отдаст деньги. И тут как раз большинство людей не смогут сделать
интуитивную оценку.
Однако, если мы будем наберем статистику по кредитам и отказам на бытовом
уровне, мы получим примерно тот же результат, как если бы люди вычисляли
вероятность по формуле Байеса. То есть, грубо, 90% людей не дадут деньги при
вероятности невозврата 90% (на самом деле немного не так, но формула там все
равно работает)
В приведенном примере с болезнью большинство людей, получив неприятный диагноз,
побежит к другому врачу. На чем, кстати, наживаются разнообразные знахари.
Использование животными байесовской логики исследовалось учеными. Вот 2 ссылки:
https://www.researchgate.net/publication/221946444_Bayes'_theorem_and_its_applications_in_animal_behavior
http://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1002282
Вторая статья как раз про социальное поведение животных.
14
НаписалDedushka_shubin7 мая 2017 в 09:20ответить
Dedushka_shubin, хммм... Да, интересно, спасибо.
1
НаписалSkyRzn7 мая 2017 в 10:00ответить
Ну у него какая–то уж очень
вольная философская трактовка, мне кажется.
А на счет вероятности: фраза "тест выдает положительный результат у 99%
больных людей и ложно–положительный у 1% здоровых" — это не полная
группа событий.
Полна группа события будет включать всех людей, прошедших тест, и будет
состоять из 4 вероятностей:
1) "те, кто был болен и получил положительный результат"
2) "те, кто был болен и получил отрицательный результат"
3) "те, кто был здоров и получил отрицательный результат"
4) "те, кто был здоров и получил положительный результат"
Из этих вероятностей мы знаем только две. Да и то в процентах не от общего
числа прошедших тест, а от числа здоровых/больных. При том, что больных на
несколько порядков меньше, чем здоровых, и поэтому в абсолютных значениях число
людей с ложно–положительными результатами будет значительно больше, чем
действительно больных.
Имхо, тут имеет место введение в заблуждение со стороны врача, сознательное или
не сознательное.
Врач вполне мог сказать, сколько людей, из получивших положительный результат,
оказались действительно больны, а не играться с цифрами. Кстати, если бы цифры
были 99% и 2%, то тоже возникли бы подозрения, что что–то ту не так.
Я понимаю, что это пример такой странный. Но, мне кажется, тут основная суть в
том, что люди могут вводить вас в заблуждение с помощью такой тактики —
подгоняя цифры и выдавая за полную группу событий то, что ей не является.
34
Написалколдун–инопланетянинvolk-kuraga6 мая 2017 в 20:04ответить
volk–kuraga, пример не про реальную ситуацию с болезнью и диагнозом, которая может выглядеть еще сложнее, а про реальную ситуацию с неспособностью среднего (т.е. необученного) человека решить эту задачу. То, что вы сейчас делаете, это примерно как увидев задачу про бассейн и три трубы, рассуждать, что в реальных бассейнах есть еще фильтр на заливе, фильтр на сливе и так далее.
8
НаписалDedushka_shubin6 мая 2017 в 22:35ответить
Dedushka_shubin, Нет. Я может в
своем комментарии много лишнего написал, но суть в том, что пример некорректный.
То, что у 99% больных тест дает положительный результат — означает, что у 1% больных он дает
отрицательный результат.
В примере не моргнув глазом заменили 1 % больных с отрицательным результатом на
один 1% здоровых с положительным. Благо, что цифры совпали. А ведь тест мог
давать положительный результат и у 2% здоровых, и у 4%. Вероятность
ложно–положительных результатов среди здоровых — никак не связана с
вероятностью положительных результатов у больных.
Это явная попытка введения в заблуждение и подмена цифр. Не важно, реальный
пример или выдуманный — в любом случае, нельзя просто так складывать
вероятности от разных групп событий.
Правильно фраза должна была звучать так:
"Среди всех, получивших положительный результат, 99% оказались больными, а
1% — здоровыми"
Тогда было бы все ясно и понятно.
7
Написалколдун–инопланетянинvolk-kuraga7 мая 2017 в 01:46ответить
volk–kuraga, Я хочу сказать,
что авторы, видимо, перегнули палку и, помимо демонстрации теоремы Байеса,
добавили еще и демонстрацию введения в заблуждение с помощью цифр.
Достаточно было заменить 1% на 2%, и тогда цифры бы не сошлись — и не было бы
путаницы.
Но видимо им захотелось сделать свой пример еще более убедительным.
Суть то тут вообще в том, что вероятность положительного теста у больных — мало
что говорит о том, больны вы или нет. Потому что неизвестно, как относится
число больных с положительным тестом к числу здоровых с ложно–положительным. В
тесте на это все натягивается теорема Байеса, хотя по сути она тут не нужна —
нужно просто посчитать все возможные исходы теста (которые я написал выше) и
соответствующий процент людей, попадающий в них. Тогда было бы очевидно, что на
тысячу человек приходится 1 больной с положительным тестом и 10 здоровых с
ложно–положительным.
Т.е., еще раз: в примере неправильно используется информация о здоровых с
ложно–положительными результатами. Это вызвано совпадением процента больных с
отрицательным и процента здоровых с ложно–положительным. Если бы процент был
разный, это бы уже не прокатило.
В итоге мы имеем, что пример демонстрирует совсем не то, о чем пост.
6
Написалколдун–инопланетянинvolk-kuraga7 мая 2017 в 02:04ответить
volk–kuraga, я еще помню, как
проходила математика — моего учителя очень бесили вопросы типа "почему е
равняется ~2,72", а меня — ответы "так надо, потом узнаешь" или
впрыгивают эти лямбды в уравнение, как черт из табакерки.
Но можно было просто сказать, что вся математика — на самом деле, фантазия,
полет мысли, выстроенная в логике, строго последовательна и формализована — для
универсальности в т.ч. Хоть такое утверждение сильно обобщено, уверен, многие
вещи я воспринимал бы иначе.
Видео из поста — это другая крайность. Круто, если бы у него там была ссылка в
описании — проходишь, а там "Добро пожаловать на уровень 2. Ну да, с
цифрами мы упростили. Следуя теореме Байеса, надо взять и т.д."
2
Написалhadabr7 мая 2017 в 03:36ответить
hadabr, Извините, ваш учитель
не мог ответить на вопрос, почему е равняется ~2,72???
Ужас. Это можно объяснить семикласснику без каких–либо проблем.
1
НаписалDedushka_shubin7 мая 2017 в 09:22ответить
Dedushka_shubin, А кстати можете объяснить? Ну мне просто любопытно стало.
5
Написалколдун–инопланетянинvolk-kuraga7 мая 2017 в 19:18ответить
volk–kuraga, есть много разных способов, но вот один: начинаем с объяснения того, что такое вообще нецелая степень. Строим несколько графиков y=a^x при разных a. Наблюдаем, насколько быстро оно растет, и пробуем выяснить, насколько же быстро. Для этого проще всего сделать табличку в Экселе и менять a. Видим, что скорость изменения y как–то похожа на сам график y=a^x. Строим обе функции, y=a^x и ее производной на одном графике. Далее утверждаем, что есть такое волшебное число, для которого скорость изменения у описывается в точности тем же уравнением, что и исходная y. Пробуем подобрать такое число. Получается где–то примерно e.
0
НаписалDedushka_shubin7 мая 2017 в 20:22ответить
Dedushka_shubin, Ну я вас понял, а вот на счет семиклассника — не уверен. :)
1
Написалколдун–инопланетянинvolk-kuraga7 мая 2017 в 23:28ответить
volk–kuraga, есть еще такое
обьяснение числа е — оно мало к чему ведет, но красиво звучит и чему–то
учит.
Вот представь себе, что ты взял кредит по пьяни под 100% годовых.
ТО есть ты думаешь, что ты взял 1 (миллион), и через год вернешь 2
=1*(100%+100%)
Но дальше банк становится хитрожопым, и пересчитывает процент каждые полгода.
Тогда ты платишь в конце года 1*1.5*1.5=2.25
Или если четыре раза в год, то (1.25)^4=2.44
Или каждый день (1+1/365)^365=2.714
Или каждый час (1+1/365/24)^(365*24)=2.71813
вот если банк начнет так делать бесконечно часто, то это будет е...
8
НаписалKalvado7 мая 2017 в 23:57ответить
volk–kuraga, Зашел за этим
комментарием.
Первый пример вообще не корректен. В основе фразы "тест выдает
положительный результат у 99% больных людей и ложно–положительный у 1%
здоровых" лежат всего лишь результаты тестирования теста перед его
выпуском для широкого применения. Так же не корректен пример с тысячей человек,
потому что там показано, что человек заболел с вероятностью 1@0 (это прямо
таки дофига для редкой болезни), а не с реальной вероятностью. В результате
пример подсовывает вывод, учитывая наши когнитивные искажения, лишь "тесту
с такой вероятностью ошибки верить нельзя".
2
Написалptitzin6 мая 2017 в 20:17ответить
volk–kuraga, не не братюня математик, тут тема такая сможешь ли ты круто поменять свою жизь
2
Написалpizzazz7 мая 2017 в 08:32ответить
pizzazz, Но... я не математик
2
Написалколдун–инопланетянинvolk-kuraga7 мая 2017 в 19:12ответить
> Этот пост, пожалуй, можно
было бы выложить и на политоту, или даже на политикс.
Да нет, в ролике же прямо говорят, что спор между людьми уверенными в чем–то на
100% бесполезен.
15
Написалtequila_Jim6 мая 2017 в 19:35ответить
tequila_Jim, это тонкий момент.
Что считать 100%? Если как личная субъективная оценка — да, это одно.
Типа, человек может быть на 100, на 101 и даже на 1 000 000% уверен, что
"я сегодня не выпью", а к вечеру — вероятности меняются.
Любой взрослый человек может покопаться в памяти и вспомнить свои прежние
убеждения, в которых он был уверен на 100%, но потом — что–то изменилось.
Где–то есть небайесово действие, какое–то арифметическое –0.0001%, которое даже
в самом убежденном человеке зарождает сомнение, через которое он может потом
изменить мнение.
Мне кажется, то, что он говорил про "людей, уверенных на 100%" —
это не имеет отношения к формуле Байеса, это не частный случай применения
формулы, а просто красивая аналогия, так как человек иррационален (даже если
формулу Байеса знает), и внутри живет не по формулам.
2
Написалxenon7 мая 2017 в 14:52ответить
Яростно плюсую любую популяризацию Байеса здесь и везде, где только можно. Это должен знать, понимать и использовать каждый. Для меня в свое время, еще в школе, это имело эффект сродни какой–то магии. Весь мир, каждое событие, прогнозы, споры стали выглядеть совершенно иначе. Потом, конечно, эмоции схлынули, но до сих пор помню то ошеломляющее впечатление, наверное что–то подобное чувствуют дальтоники, впервые увидевшие цвета, или глухие, впервые услышавшие музыку. Это очень круто, да, контринтуитивно, но очень просто и эффективно. Спасибо автору за невольное напоминание об этом моменте, да и вообще — это очень и очень актуально в наши времена.
13
Написалqwasy6 мая 2017 в 20:26ответить
qwasy, К сожалению мысленный опыт Байеса нарушается, если ассистент врет про мячи — достаточно небольшого искажения поступающих данных и ошибка будет накапливаться. Так же мысленный опыт не сработает, если ассистент вывалит на стол сразу корзину мячей — информация начинает поступать в таких количествах, что Байес не успевает ее обрабатывать и обновлять свое знание о мире. Ну и уж тем более не сработает, если ассистент выстрелит ему в голову из пистолета, пользуясь тем, что Байес сидит к нему спиной. Велкам в наш реальный мир.
11
Написалptitzin6 мая 2017 в 20:37ответить
ptitzin, да знаю я, чай не мальчик уже. Говорю же — "еще в школе", "потом эмоции схлынули". Просто ощущение очень прикольное, когда что–то смутно, интуитивно понимаешь, а потом раз — и все это смутное становится кристально чистым — что иногда некоторые вещи можно просчитать, а не просто почувствовать. Для подростка подобные вещи в новинку и впечатляют весьма — как первый секс, первый стакан портвейна, первое разочарование в людях. Просто вспомнилось. Ну и нечастно бывает, как я потом понял, чтобы первое знакомство с вероятностным анализом началось именно с Байеса. Это пробудило во мне интерес к теории игр, к математической статистике — да чего там говорить, я буквально через пару месяцев начал считать и запоминать карты при игре в дурака, что просто неимоверно подняло мой рейтинг побед среди дворовых любителей подкидного. А потом, когда попал в компанию преферансистов, они мне не поверили, что я раньше никогда в преферанс не играл. В общем, ничего сверхъестественного, просто ностальгия по одному из первых жизненных открытий.
1
Написалqwasy6 мая 2017 в 21:23ответить
qwasy, > первое знакомство с
вероятностным анализом началось именно с Байеса
Вообще–то оно ДОЛЖНО начинаться с Байеса, хотя бы с объяснения чем классическая
и байсовская вероятность различаются. А то так и будут шутить про блондинку и
вероятностью встретить динозавра.
0
Написалptitzin6 мая 2017 в 21:40ответить
ptitzin, воот, я ж про это же. Мне офигенно повезло, что оно началось именно с этого. Обычно, как показала практика, начинается с чего–то более элементарного, как бы, с примеров про бросание монетки 1 раз, 10раз и 1000, например. Наш преподаватель вышки в универе, когда я с это с ним обсуждал, говорил что Байес слишком сложен для понимания людьми, не знакомыми с математически формализованным понятием классической вероятности. А мой случай он сравнивал со школьником, который вместо первого класса попал сразу в пятый–шестой. Как по мне — преувеличение и консерватизм, но именно так он и говорил. А я на тот момент был, скажем так, гуманитарно ориентирован, математику считал нуднейшей хренью, к которой я не способен и которая мне не нравилась, и даже о элементарнейших вещах, самых что ни на есть основах тервера не задумывался, мне было не интересно. И тут бабах — поворот на 180 градусов, я изменил свое отношение целиком и полностью. Можно сказать, что я открыл для себя красоту и величие математики благодаря Байесу. Математиком я так и не стал, но увлечение осталось на всю жизнь, и очень мне помогало в самых различных областях и сферах деятельности.
0
Написалqwasy7 мая 2017 в 00:02ответить
qwasy, меня это видео и его
содержание натолкнуло на похожую мысль.
Вот в развитых странах уже будущность, автоматизация, вся фигня. Внезапно
человек может на рынке труда не так много и предложить — что не могут
роботы — собственно, человечность (рынок услуг), креативность и системное
мышление (особенно на срезе дисциплин).
И вот с двумя последними интересное — всё больше по жизни сталкиваюсь, что
проблема не то, что ты чего–то не знаешь или не умеешь, а то, что ты не знаешь,
что ты чего–то не знаешь.
Грубо говоря, представим себе математика, собравшегося решить теорема Ферма. В
его мире известен только раздел диффуров.
2
Написалhadabr7 мая 2017 в 02:52ответить
hadabr, о да. Системное мышление в междисциплинарном взаимодействии — крайне важная штука, и дефицит кадров, продвинутых в этом, еще долго будет актуален, кмк. Вот, к примеру, психология — в обывательском понимании абсолютно гуманитарная дисциплина, которая к математике никакого отношения не имеет, и даже рядом не стояла. Но это только на первый взгляд. Нам преподавали в универе матстат и тервер в том же объеме, что и на мехмате, и я видел, как "плавали" мои одногрупники, в большинстве своем подобного не ожидавшие. Как же негодовала одна студентка, круглая отличница на тот момент, у которой с вышкой был полный швах. "Зачем нам столько математики, мы же психологи! Они издеваются!" У меня же, уже успевшего отучиться на инженера на тот момент, было противоположное мнение — я видел, что преподаватель откровенно жалеет нас, и ставит тройки и четверки в таких ситуациях, в которых в техвузе отправили бы на пересдачу без лишних разговоров. Я считал, что математики мало, что надо обязательно прививать математическое мышление — и многие потом, ближе к диплому, со мной соглашались. Обработка результатов тестирования при тысячах опрошенных, различные статистические выборки, Гаусс, то же Байес — это огромный пласт в определенных направлениях психологи, та же социальная психология, к примеру. Можно, конечно, отдавать это на аутсорс, особенно если в дальнейшем заниматься подобным не планируешь, но как же помогают и экономят время продвинутые навыки самостоятельного решения таких задач! В общем, я считаю, что за этим будущее — жесткое разделение на гуманитариев и технарей должно исчезнуть рано или поздно, и упор на междисциплинарность станет обязательным и обыденным. Это уже происходит, но основная часть этого пути еще не пройдена.
12
Написалqwasy7 мая 2017 в 10:37ответить
qwasy, В России просто еще с
советских времен пошло неуважение к гуманитарным специальностям и точка зрения,
что туда идут те, кто не смог стать инженером.
Ну типа "раз ты танки и ракеты проектировать не можешь, иди на
гуманитария — все хоть какая–то польза будет". Я даже знаю случаи,
когда родители отговаривают детей поступать на не–технические
специальности — что мол, никому они не нужны, работу потом не найдешь, там
только тупые учатся и т.д.
Ну, правда, я достаточно давно учился — сейчас может и не так все плохо.
3
Написалколдун–инопланетянинvolk-kuraga7 мая 2017 в 19:27ответить
volk–kuraga, некоторое время всё было ещё хуже, но с перекосом в другую сторону — все как подорваные стремились в экономисты да юристы, отчего их явный переизбыток случился, а вот инженеры толковые до сих пор в некотором дефиците. Сейчас ситуация вроде как выравнивается, я плотно не мониторил, но по знакомым скажу — очень многие детей ориентируют учиться на технические специальности. Если это отражает общую ситуацию по стране, то не может не радовать. Но, повторюсь — будущее за междисциплинарностью. Многие профессии в не столь отдаленной перспективе отомрут, будучи компьютеризированными и автоматизированными, а нужны будут в основном те, кого модно называть "смарт–менеджер" — творчески ориентированные технари, ну и технически продвинутые гуманитарии, которые, к примеру, и накодить что–то смогут, и ЧПУ настроить, и 3d модельку в каком–нибудь Zbrushдля этого ЧПУ сваять. В общем, нас ждут интересные времена — если доживем, и если политики все в очередной раз не отправят коту под хвост.
0
Написалqwasy8 мая 2017 в 00:29ответить
Если я бы глянул видео в
средней школе, точно увлекся бы на время матстатистикой. Может, перешел бы к
эконометрии или Data mining, может, бы бросил, но спустя годы в совершенно
другой сфере деятельности нашел бы ключ к разгадке, а иначе — никак.
Ясное дело, что обучить человека всему не нужно/невозможно — в споре
Шерлока и Ватсона "Вы, что не читаете романы"
Шерлок куда актуальней. Замечательная возможность, если в образовании будущего,
где всё учится соответственно запросу — быстрей, но
"узкоспециализированей" — рядом с основным потоком обучения
существовал бы некий шум из подобных видео — на грани доступности и
информативности в несколько слоев "погружения" (доступность⟶информативность). Когда даешь
себя осознанно увлечь.
0
Написалhadabr7 мая 2017 в 03:09ответить
ptitzin, ба–ба–ба баес в здании...
0
Написалpizzazz7 мая 2017 в 08:35ответить
А еще Байесиановская статистика помогает вытаскивать сигнал из шума — примерно так:
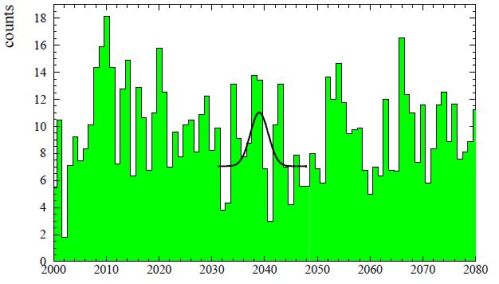
5
НаписалKalvado6 мая 2017 в 18:13ответить
Kalvado, можете порекомендовать
что–то почитать на эту тему?
Очень уж картинка напоминает задачу, с которой недавно сталкивался. Впрочем,
может быть, я неудачно гадаю по картинке, и здесь совсем не то. Задача
была — выделить импульсный сигнал с длительностью в пару отсчетов. Решение
"в лоб" работает, но догадываюсь, что далеко не лучшим образом, а с
теорией обработки сигналов не знаком.
0
НаписалSkyRzn6 мая 2017 в 23:49ответить
SkyRzn, с моей точки зрения, картинка это (не очень удачное) натягивание совы на глобус. Я, по–видимому, не одинок в таком мнении: мужик картинку опубликовавший Нобеля еще не имеет, хотя если бы это было правдой как он говорит — он бы должен был получать ближайшего. Бо тема сильнейшая.
0
НаписалKalvado7 мая 2017 в 01:48ответить
Kalvado, Не знаю, что у вас там исследуют, но черная кривая перевернута.
0
Написалдилетантshadows_and_dust7 мая 2017 в 05:49ответить
shadows_and_dust, мне тоже как
кажется — но автор утверждает что это 3 сигма и оно опубликовано в приличном
журнале
upd: посмотрел — на эту работу 894 ссылки.
ВОСЕМЬСОТ
ДЕВЯНОСТО ЧЕТЫРЕ!!!
4
НаписалKalvado7 мая 2017 в 06:00ответить
Kalvado,
Если статьи цитируют, значит это кому–нибудь нужно.
0
Написалдилетантshadows_and_dust7 мая 2017 в 08:38ответить
shadows_and_dust, если бы быть
уверенным что тут правда — это нобель, без дураков.... Но статья 2003
года.
12 лет накапливали статистику, 1е25 лет период полураспада...
0
НаписалKalvado7 мая 2017 в 09:09ответить
У меня тоже такая фигня была: а лечился от трепака, а две подруги и жена сказали, что у них ничего нет. Жалко я тогда про теорему Байеса не знал.
3
Написалiangel6 мая 2017 в 22:48ответить
Зачем плодить сущности без
необходимости.
Закон Орра: "Что бы ни думал думающий, доказывающий это докажет"
3
Написалbrooke bond7 мая 2017 в 00:00ответить
brooke bond, что бы ни думал
думающий о необходимости плодить сущности, доказывающий это докажет. И более
того, что бы ни думал думающий о законе Орра, доказывающий докажет и это.
С учетом этих сентенций, что там с необходимостью плодить сущности и законом
Орра получается?
2
Написалqwasy7 мая 2017 в 00:46ответить
