Функциональный анализ для самых маленьких
Функциональный анализ для самых маленьких
5 0 0 5 4 4 4 0 5 Относится к разделам:
В математике существует превеликое множество всяческих разделов, подразделов, направлений и течений. Самым трудным из них в рамках университетского курса прикладной математики для меня оказался функциональный анализ. И, по всей видимости, не для меня одного, раз сей предмет получил шутливое название “анальный функционализ” среди студентов околоматематических специальностей. Экзамен по нему я сдал аж с четвертого раза, из–за чего потерял маленькую, но очень вожделенную стипендию на целый семестр. Ну а более–менее ясное понимание идей и методов этого раздела математики пришло ко мне лишь через пару лет после окончания курса. Этим своим видением сего премудрого колдунства под гордым названием “Функциональный анализ” (далее “функан”) я бы и хотел поделиться с почтенной публикой. 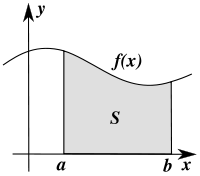 Представление художника об определенном интеграле. Аналогичным образом, если постараться, можно нарисовать себе картинку многих математических абстракций — производных, векторов, тензоров и даже, при желании, некоторых алгебраических структур, наподобие групп . Все это вполне себе прекрасно помещается в нашем воображении и дает более–менее правдоподобное представление о рассматриваемом объекте. Но когда дело доходит до функана, как и в случае с квантовой механикой, наступает облом — картинку изучаемых там процессов воображение рисовать наотрез отказывается. Дабы не быть голословным, давайте вместе попробуем состряпать типичный объект, изучаемый этой дисциплиной. Строительство начнем с простого. Возьмем обычный отрезок — кусочек прямой, ограниченный двумя точками. Можно обозвать его более заумно — часть одномерного пространства, ограниченного с двух сторон. Про размерность пространства, думаю, все имеют определенное представление, останавливаться здесь не будем. Замечу лишь, что наше интуитивное представление о размерности пространства совпадает с точным занудным математическим определением. Теперь, усложним наш объект — добавим к нему еще одно измерение и ограничим его там точно так же с двух сторон. Мы получили квадрат на плоскости, для понимания происходящего по–прежнему не требуется повышенное содержание пядей во лбу. Добавим еще одно измерение и мы увидим обычный куб. Правда если присмотреться, то обычный он только для нас с вами. А, скажем, для двумерных героев сериала “Симпсоны” трехмерный куб является объектом фантастическим, находящимся за гранью их понимания. Они этому факту даже кусочек хэллоуиновской серии . Двигаемся дальше — нарастим еще одно, уже четвертое измерение. На сей раз мы имеем нечто интересное под названием “гиперкуб” или “ тессеракт ”. Вообразить этот объект может уже далеко не всякий. В расплющенном до нашего трехмерного пространства виде эта штука выглядит примерно так:  Плоский тессеракт Кстати, вы заметили, что сделав всего несколько шагов к построению элементарнейшего объекта функционального анализа, наше воображение уже добралось до своего предела? Вот эти шаги, на картинке: 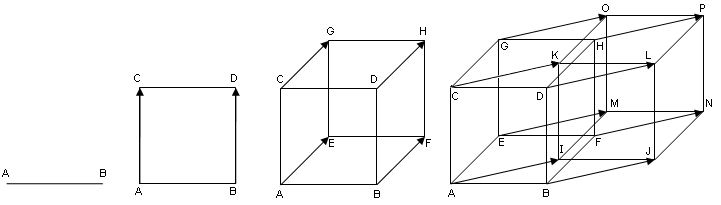 Рождение гиперкуба. Ну что, не устали? Тогда двигаемся дальше. Продолжим наращивать измерения — пятое, шестое, седьмое, …, сто тридцатое, …, семь миллионов девятое,..., , ЧислоГрэммаПлюсПервое, ….. Наш гиперкуб уже не просто гиперкуб, а супер–пупер–гиперкуб, но даже и эта штука не настолько крутая, чтобы на нее обратили внимание нерды с кафедры функционального анализа. И что же делать? Как нам добраться до цели? Выход один: сделать количество измерений равным бесконечности. За последнюю фразу, вообще говоря, на математическом симпозиуме можно получить по щщам с вертухи, т.к. равной бесконечности никакая величина быть не может, ибо бесконечность — это процесс. Но мы не на симпозиуме и я позволю себе пошалить и вдоволь покидаться умными и не очень словами не особо переживая за их точный математический смысл. Да простит меня за эти шалости почтенный Николя Бурбаки . Итак, мы добрались до финиша, построив какую–то непонятную хреновину в виде куба с бесконечным количеством сторон. Забавный каламбур — несмотря на то, что всю дорогу у нас был куб, полученную сущность математики почему–то именуют шаром. Такой вот шар бесконечномерного пространства, а также само бесконечномерное пространство и действующие в нем всякие фиговины, под названием “отображения” — это и есть та самая , которую изучает функан. Такие дела. Теперь вы имеете самое минимальное представление о том, над чем горбатятся яйцеголовые очкарики на средних и старших курсов мехмата. Дальше, как вы догадываетесь, будет только хуже. Согласен, функан расширяет сознание похлеще некоторых веществ. Спасибо его основателям во главе со Стефананом Банахом за бесплатный опиум. Сам функан, как это ни парадоксально, задумывался из желания унифицировать, и тем самым упростить жизнь математиков. Все дело в том, что огромная часть задач, встречающихся на практике, начиная от того, сколько бутылок водки надо купить на компанию из 14ти человек, чтоб всем хватило, заканчивая расчетом двигателя для Боинга, сводятся к различного рода уравнениям — алгебраическим, дифференциальным, интегральным и т.п.. На первый взгляд, может показаться, что все эти уравнения очень разные. Действительно, посмотрите, как они выглядят внешне:  Алгебраическое уравнение  Дифференциальное  Уравнение в частных производных 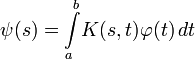 Интегральное уравнение Бывают и другие типы уравнений, а так же целые системы из них, и они так же внешне не похожи на представленные здесь. Но это только на первый взгляд. Дотошные математики давно стали замечать, что несмотря на всю кажущуюся непохожесть, решения абсолютно разных по своей природе уравнений ведут себя настораживающе сходным образом. Например, если А и В — это решения какого либо из приведенных выше примеров, то их сумма А+В тоже будет решением этого примера. И даже не просто сумма, а вот такая штука k*A+m*B, где k и m — это обычные числа (множители), так же сгодится под решение. И вот, зацепившись за столь незначительный, с первого взгляда, факт, неутомимые матанщики умудрились построить целую теорию, позволяющую изучать все эти совершенно разные уравнения как одно и то же, не вдаваясь в их абсолютно разную природу и происхождение. В конце XIX — начале ХХ века до математиков медленно начало доходить, что во всех этих случаях происходит один и тот же процесс, записываемый символически вот так:  Операторное уравнение 1–го рода Расшифрую. Берется неизвестное х, затем оно пропускается через какую–то ерундовину F(), а на выходе из нее должна получиться некая заранее известная величина y. Задача — найти х. Кому как, но мне сей процесс удобно представлять при помощи мясорубки, где х — ингредиенты для фарша (неизвестное), F() — сама мясорубка, y — получившийся фарш: 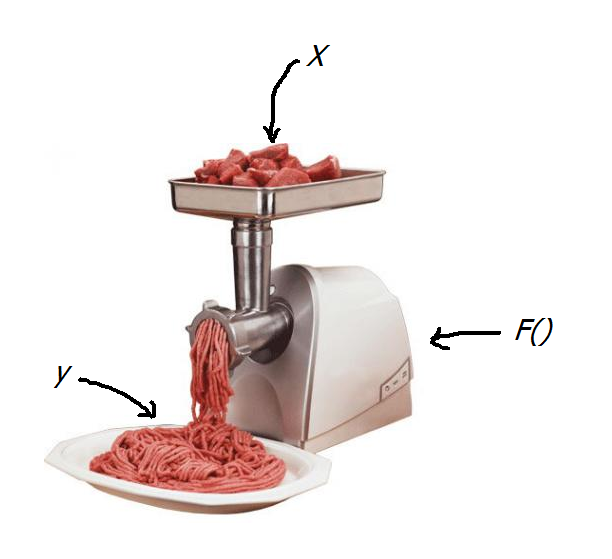 Операторное уравнение 1–го рода Забавно, но все принципы функционального анализа одинаково хорошо работают как для обычной мясорубки, так и для дифференциального уравнения. Поэтому, производство фарша будет хорошей аналогией для демонстрации прелестей сабжа. Предметы в бесконечномерном пространстве ведут себя не так как в конечномерном. Например, теряет смысл понятие объема. В самом деле квадрат со стороной 2 имеет площадь (2D–объем) 2х2=4, объем 3D куба со стороной 2 равен 2х2х2=8, 4D, как не сложно догадаться 2х2х2х2=16 и т.д.. Соответственно, объем бесконечномерного куба будет равен бесконечности. В кубе с ребром 1 можно уместить бесконечное количество кубов с ребром 0,5, и при этом они не будут друг друга даже задевать. Классический матан на этом месте сдувается — ему же надо чтоб были бесконечно малые, пределы, вот это вот все (если кто помнит), а какие тут могут быть пределы, если даже бесконечно малый куб при ближайшем рассмотрении оказывается беспредельно большим? Ясен пень, что никаких. Вообще, функан соотносится с обычным матаном примерно так же, как теория относительности с ньютоновской механикой. Как при малых скоростях Эйнштейн=Ньютон, точно так же и в конечномерных пространствах функан=матан. Функциональный анализ имеет в своем арсенале несколько очень важных для приложений результатов, благодаря которым решается множество серьезных проблем в современных математике и физике. Жаль, что не все из них я смогу объяснить на примере фарша с мясорубкой. Вернемся к нашим аналогиям. Итак, фарш — это продукт, который состоит из множества ингредиентов — свинина, говядина, баранина, соль, сало, перец и т.п.. Представим, что таких ингредиентов в нашем фарше смешивается бесконечное количество. Стало быть каждый конкретный рецепт приготовления фарша — это своего рода точка бесконечномерного пространства: если по оси говядины отложить столько–то кг, по оси свинины столько–то, по оси сала столько–то и т.д. мы получим точку в бесконечномерном пространстве по аналогии с трехмерной системой координат, где вместо осей XYZ идет бесконечное количество осей с ингредиентами. 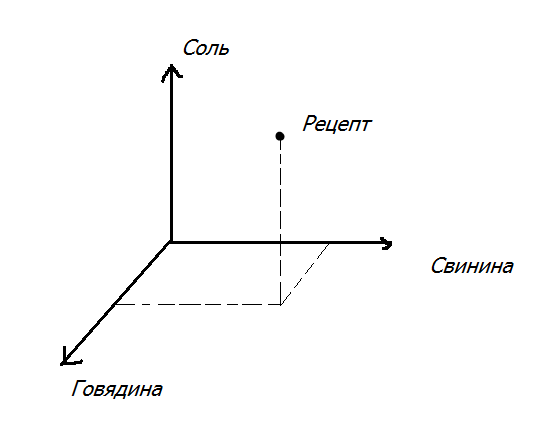 Трехмерная система координат. Может быть расширена до бесконечномерной неограниченным добавлением осей. Мясорубка — это предмет, который пропускает фарш через себя и тем самым меняет его состав. Пускай у нас будет немного волшебная мясорубка: скажем, она сможет менять количество ингредиентов в фарше — уменьшать объем соли или увеличивать содержание свинины в фарше, или все вместе, или все наоборот. Если наш фарш математики привыкли именовать “точкой” или “вектором”, то мясорубку они будут называть “оператором”. Попытаемся сформулировать в кухонных терминах одну из главных теорем функционального анализа — теорему Банаха об обратном операторе. Для солидности приведем ее обычную формулировку (прошу вас в нее не вдумываться — она здесь просто для картинки): Теорема Банаха об обратном операторе. Пусть X, Y — банаховы пространства, оператор A ∈ L(X, Y ) взаимооднозначно отображает X на все Y (т.е. KerA = {0}, ImA = Y ). Тогда A непрерывно обратим. Несмотря на всю суровость и непонятность формулировки, обозначает она лишь то, что если во–первых, мощность мясорубки не бесконечна, и во–вторых, при помощи этой мясорубки теоретически можно получить любой фарш с любой рецептурой, если подобрать правильные компоненты, то по–любому найдется такая волшебная антимясорубка, которая сможет восстанавливать из фарша исходные ингредиенты. Проще говоря, эта теорема дает условия, при которых у мясорубки существует ей обратная антимясорубка. Естественный возникающий при этом вопрос: на кой оно нам вообще надо? А надо вот зачем. Если помните, то наша основная задача в мясорубочном процессе — это зная мясорубку и получившийся фарш, найти исходные для этого фарша ингредиенты. Иными словами мясорубка и фарш — это известные величины, ингредиенты — неизвестная величина.Если наша мясорубка подходит под условия теоремы, то гарантированно для нее найдется какая–то антимясорубка, пропустив через которую известную величину “фарш”, мы получим искомую величину “мясо”. Забавно, что теорема не дает никакого понимания, как будет выглядеть сия антимясорубка, и как с ее помощью решить поставленную задачу. Теорема лишь говорит, что решение просто существует и все, какое оно — никто может и не знать. И математиков это вполне устраивает — для них порой узнать существует ли решение задачи или нет, важнее отыскания самого решения. На эту тему у них даже есть самоироничный анекдот: В гостинице, куда поселились инженер, математик и физик, возник пожар. Инженер выбегает в коридор, видит на стене пожарный шланг, хватает его, открывает воду и заливает очаг возгорания. Физик, быстро прикинув объем горючих веществ, температуру пламени, теплоемкость воды и пара, атмосферное давление и т.п., наливает в стакан из графина строго определенное количество воды и заливает огонь этой водой. Математик выскакивает в коридор, видит на стене огнетушитель, и, обрадовано воскликнув: "Решение существует!", спокойно возвращается в номер... Второй важный результат функана, который я попытаюсь объяснить на кулинарной основе, это спектральная теорема, являющаяся одним из главных кирпичей в фундаменте квантовой механики. Перед ее изложением я приведу несколько дополнительных понятий: компактное множество, базис пространства и собственные значения и векторы оператора. Начнем с первого. Помните, выше мы увидели, что любой куб/шар бесконечномерного пространства имеет бесконечный объем? Выясняется, что, однако, не все объекты в функане бесконечны внутри. Самый простой пример — это конечномерный куб в бесконечномерном пространстве — его объем ограничен. Другие примеры конечного объема в бесконечномерном пространстве имеют более сложное строение, похожее на кусок швейцарского сыра, в котором дырок больше, чем самого сыра, из–за чего общий объем получается не таким уж и большим. Такие объекты называются компактными множествами (или компактами). Математикам удобнее считать, что компакты содержат свою границу, т.е. кожуру. Таким образом, типичным представителем компакта можно считать неочищенную от кожицы краковскую колбасу, в которую забыли добавить сало, и теперь вместо белых пятен у нее на срезе красуются пустоты.  Типичное компактное множество Мясорубка (оператор) тоже может быть компактной. Ее так называют, если она умеет из фарша делать колбасу (по заумному: из шара делает компакт) Второе нужное нам понятие — это базис. Базис, как не сложно догадаться, является однокоренным к слову “база”, т.е. “основа”. Так вот, базис — это набор ингредиентов, из которых мы собираемся с помощью мясорубки что–нибудь приготовить. Например, по–хорошему, краковская колбаса готовится из свинины, говядины, соли, перца и т.п.. Это и есть базис, на котором мы можем напридумывать кучу рецептов разных колбас. Однако, некоторые недобросовестные производители умудряются приготовить колбасу из совершенно другого набора продуктов: кенгурятины, барсучьего жира, сои, ароматизаторов, идентичных натуральным, и т.п.. На вкус эта “колбаса” будет неотличимой от “настоящей” краковской. Просто, она будет приготовленной на другой элементной базе. Так вот, эти два рецепта математики будут называть разложением краковской колбасы двум по разным базисам. Фактически это одна и та же точка, но только в разных системах координат. 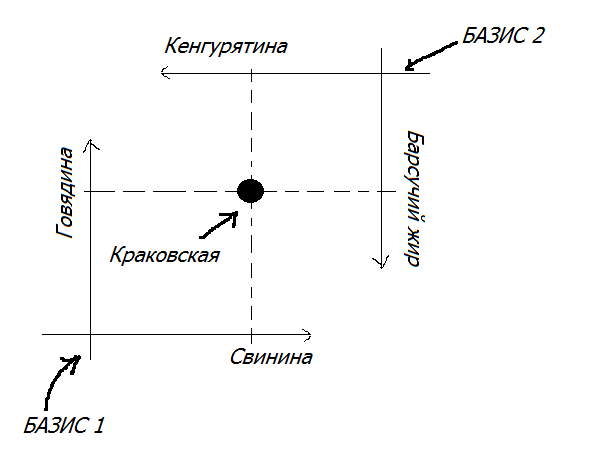 Краковская колбаса при переходе от одного базиса к другому. Другая аналогия: одна и та же температура по Цельсию и Фаренгейту — температура одна, а цифры разные. Третье понятие — собственные векторы оператора. Их можно объяснить следующим образом: собственные векторы — это векторы, в направлении которых мясорубка не меняет химического состава выходного продукта. Примеры: 1. Если мы засунем в мясорубку килограмм свинины, и на выходе получим тоже свинину, причем неважно, килограмм, 5 или 10, то свинина — это собственный вектор, т.к. химический состав не поменялся, была свинина на входе, осталась свинина на выходе. 2. Если мы засунем докторскую колбасу, и на выходе будем иметь тоже докторскую, то докторская колбаса тоже будет собственным вектором — состав же не поменялся. 3. А вот если на входе мы имеем краковскую, а на выходе любительскую, то краковская собственным вектором не будет — хим. состав поменялся же. В общем, собственные вектора — это вектора, на которые оператор действует как множитель: увеличивает или уменьшает его длину (в нашем случае вес). В этих направлениях КПД мясорубки максимален. Собственное число — это то, на сколько сильно меняется собственный вектор при прохождении через мясорубку. Если мы засунули килограмм свинины, а на выходе получили пять килограмм, то собственное число равно пяти. Теперь мы обладаем достаточным багажом знаний для осмысления самой спектральной теоремы. В скучной формулировке она звучит следующим образом: Спектральная теорема. Пусть A является компактным самосопряжённым оператором в гильбертовом пространстве V. Существует ортонормированный базис пространства V, состоящий из собственных векторов оператора A. При этом все собственные значения вещественны. Не очень понятно, правда? На наших гастрономических аналогиях это означает, что если наша мясорубка умеет делать краковскую колбасу, то из ее собственных векторов можно составить такой базисный набор продуктов, который окажется самым удобным при работе с этой мясорубкой из всех прочих. Краковскую, напомним, можно приготовить из многих наборов продуктов: из божьей росы и одуванчиков, либо из пингвиньего жира и сои и т.д.. Но проще всего, с точки зрения трудозатрат на раскручивание мясорубки — это из говядины и свинины. И вот такой вот оптимальный набор продуктов для каждой конкретной задачи, и будет называться базисом из собственных векторов мясорубки (оператора). А спектральная теорема лишь указывает на существование и характер этого оптимального набора ингредиентов (базиса из собственных векторов) у отдельных видов мясорубок. Эти собственные значения и вектора играют огромную роль в изучении физических процессов. Например, различные состояния элементарных частиц в квантовой физике — это различные собственные векторы квантовых мясорубок (операторов) Шредингера. А частота, с которой струна музыкального инструмента издает звук — это собственное значение мясорубки (уравнения), описывающей колебание струны. Я привел всего пару фактов из функционального анализа, которые оказали огромное влияние на другие разделы научного знания. Конечно, у функана есть множество других, не менее важных достижений о которых не так–то просто доходчиво поведать в двух словах. И количество этих достижений неуклонно растет. Результаты, приведенные выше — это результаты лишь первой половины ХХ века. Современный функан ушел далеко вперед. Сейчас это не просто общая теория разрешимости уравнений. Нынешний функциональный анализ — это основной язык современной математики и физики, на котором формулируются результаты не только теории дифференциальных уравнений, но и результаты алгебры, геометрии, теории вероятностей, квантовой механики, теории струн и так далее. Список можно продолжать очень долго. Любой современный учебник по этим дисциплинам говорит языком бесконечномерных пространств и действующих в них операторах (соответственно языком фаршей и мясорубок). Такие дела. Я очень надеюсь, что у меня получилось хотя бы немного приоткрыть тайну происходящего в высших разделах математики, и при этом продемонстрировать истинную внутреннюю простоту математической науки, несмотря на внешний пафос ее языка с множество непонятных символов и сложных слов. В общем, учите математику, она ум в порядок приводит (с). |
Рекомендовал: nan
Ссылки на материалы внешних ресурсов:
Вставить свой комментарий в эту страницу (только для unlimited)
Экспертов: 1 Об авторе: Статьи на сайте Форнит активно защищаются от безусловной веры в их истинность, и авторитетность автора не должна оказывать влияния на понимание сути. Если читатель затрудняется сам с определением корректности приводимых доводов, то у него есть возможность задать вопросы в обсуждении или в теме на форуме. Про авторство статей >>.
Тест: А не зомбируют ли меня? Тест: Определение веса ненаучности
В предметном указателе: Асимметрия мозга | Иванов В.В. Бессознательное, функциональная асимметрия, язык и творчество | Периодизация психического развития с точки зрения онтогенеза функциональной асимметрии полушарий | Рецепторы функциональной системы сна | Схема основных функциональных блоков в организации адаптивности поведения | Функциональная анатомия сенсорных систем Иваничев Г.А | Анализ личности | Анализ и синтез, идеализация, обобщение, абстрагирование как методы научного познания | Выготский Л.С. Искусство и психоанализ | Книга Махариши Путеводный свет гималаев Критический анализ | Новый фильтр АГС Яндекса: исследование 90к доноров, анализ и отличия от АГС-40 | О постоянстве скорости света. Анализ постулатов Эйнштейна | Без веры нет духовности | Безусловная вера | божестевенный акт творения | Виртуальные шаблоны понятий | Журнал Достижения науки, техни... | Непознаваемое | Новости науки и техники | О мистике, ее сути и свойствах | Путь самосовершенствования | Самосознание личности | Апгрейд обезьяны. Большая история маленькой сингулярности Никонов А.П. | Здоровье. МАЛЕНЬКИЕ СЕРЕНЬКИЕ КЛЕТОЧКИ ТОЖЕ ХОТЯТ ЕСТЬ | Маленькая вера. Интервью с Кристофером Хитченсом | Маленькая и большая ложь патриарха Кирилла | Маленький Мук
Последняя из новостей: Трилогия: Основы фундаментальной теории сознания.
| Обнаружен организм с крупнейшим геномом Новокаледонский вид вилочного папоротника Tmesipteris oblanceolata, произрастающий в Новой Каледонии, имеет геном размером 160,45 гигапары, что более чем в 50 раз превышает размер генома человека. | Тематическая статья: Тема осмысления |
Рецензия: Рецензия на книгу Майкла Газзанига Сознание как инстинкт | Топик ТК: Матрица, как симулякр-среда для симулякров |