Монадные кристаллы
Монадные кристаллы
http://www.milogiya2008.ru/monad_kristal.htm
1. МИР
КРИСТАЛЛОВ
1.1.ЧЕТЫРЕ СТИХИИ
КРИСТАЛЛОВ
Бесконечно богатый мир монадных кристаллов порождается их
четырьмя генетическими основаниями, из которых. по образу и подобию, формируется этот
бесконечно сказочный мир монадных кристаллов.
Ниже приводятся некоторые первые
представления о монадных кристаллах и их
формах.
1.2.МОНАДНЫЕ
ФОРМЫ
Анализ монадных форм
выявляет одно очень интересное явление. Оказывается, что вся эволюция монадных
форм колеблется между двумя типами совершенных форм. Один тип форм
составляют звездные тетраэдры (куб, на плоскости - квадрат), а другой -
простые тетраэдры (на плоскости - треугольник).
Совершенная форма кристаллов проявляется в их
симметрии. На рисунке ниже приведены 4 способа изображения молекулы
метана.
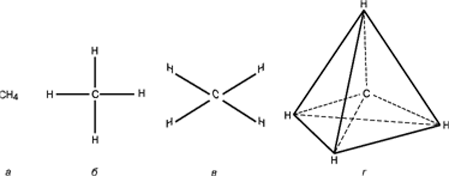 а) химическая формула;
б) структурная формула;
в) реальная схема молекулы;
г) пространственное расположение атомов в
молекуле.
Из последней схемы видно, что в молекуле
метана каждая вершина может быть вершиной
тетраэдра.
Тетраэдр является
основой совершенных форм кристаллов нашего мироздания. Кроме того, из этих
схем непосредственно видно, что "четыре стихии" порождаются "Пятой стихией". И
это не случайно (Пирамида
Силы). Эволюция монадных форм все свои творения порождает по образу и
подобию, используя природные операционные механизмы Единого
закона.
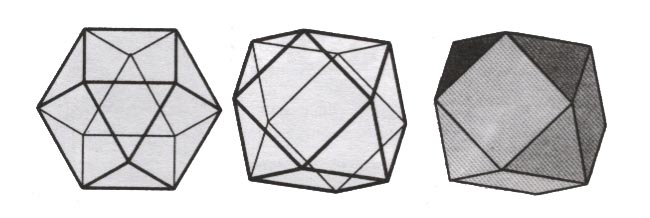
Хотелось бы отметить
также смешанные монадные форму, одной из которых является кубоктаэдр
(рис.1).
а) химическая формула;
б) структурная формула;
в) реальная схема молекулы;
г) пространственное расположение атомов в
молекуле.
Из последней схемы видно, что в молекуле
метана каждая вершина может быть вершиной
тетраэдра.
Тетраэдр является
основой совершенных форм кристаллов нашего мироздания. Кроме того, из этих
схем непосредственно видно, что "четыре стихии" порождаются "Пятой стихией". И
это не случайно (Пирамида
Силы). Эволюция монадных форм все свои творения порождает по образу и
подобию, используя природные операционные механизмы Единого
закона.
Хотелось бы отметить
также смешанные монадные форму, одной из которых является кубоктаэдр
(рис.1).
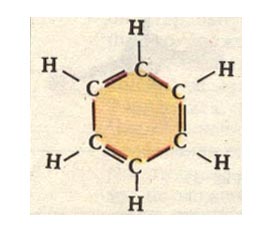
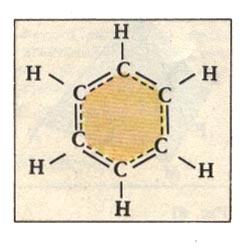 Рис. 2
Рис. 3
На первый взгляд такая структура не
должна быть симметричной, т.к. молекулы углерода в бензольном кольце
связаны не одинаковыми связями (одинарными и двойными). Это должно
искажать структуру кольца. Но этого не происходит. Коррекция формы
осуществляется на следующем "этаже", за счет обобществления бензольным кольцом
шести электронов, не занятых в локализованных связях между атомами, а способных
свободно перемещаться по бензольному кольцу, как бы демонстрируя наличие некой
силовой линии в кристалле (рис. 3). Штриховые линии обозначают наличие не
локализованной связи, возникающие за счет обобществления шести электронов.
Почему они обобществляются? Почему возникают подобные
силовые линии?
Но разные кристаллы не обязательно
формируются разными элементами. Пример, алмаз и графит. Различие в их
свойствах связано исключительно с различием их кристаллической
структуры. Кристаллическая решетка, обратите внимание, представляет собой
природный трехмерный орнамент. Заметим также, что всего существует
семь типов симметрии повторяющихся рисунков в орнаменте, которые носят
название бордюров. Можно ли сказать, что это тоже случайность, или совпадение
?
Рис. 2
Рис. 3
На первый взгляд такая структура не
должна быть симметричной, т.к. молекулы углерода в бензольном кольце
связаны не одинаковыми связями (одинарными и двойными). Это должно
искажать структуру кольца. Но этого не происходит. Коррекция формы
осуществляется на следующем "этаже", за счет обобществления бензольным кольцом
шести электронов, не занятых в локализованных связях между атомами, а способных
свободно перемещаться по бензольному кольцу, как бы демонстрируя наличие некой
силовой линии в кристалле (рис. 3). Штриховые линии обозначают наличие не
локализованной связи, возникающие за счет обобществления шести электронов.
Почему они обобществляются? Почему возникают подобные
силовые линии?
Но разные кристаллы не обязательно
формируются разными элементами. Пример, алмаз и графит. Различие в их
свойствах связано исключительно с различием их кристаллической
структуры. Кристаллическая решетка, обратите внимание, представляет собой
природный трехмерный орнамент. Заметим также, что всего существует
семь типов симметрии повторяющихся рисунков в орнаменте, которые носят
название бордюров. Можно ли сказать, что это тоже случайность, или совпадение
?
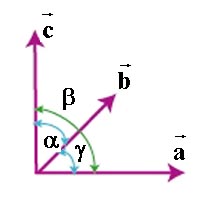 рис. 4
Здесь a, b,c,
длины ребер элементарной ячейки, а
рис. 4
Здесь a, b,c,
длины ребер элементарной ячейки, а 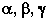 - углы между
ребрами ячейки.
Наукой установлено всего 7 кристаллографических
систем, получаемых из этой элементарных ячеек, отличающихся друг от друга длиной
сторон и углами между ними. Но почему-то снова появляется число 7? За этим скрывается закономерность, порождающая эти
кристаллографические системы, или это случайность? В этих системах каждый кристалл характеризуется наличием
определенных осей симметрии.
Куб:
- углы между
ребрами ячейки.
Наукой установлено всего 7 кристаллографических
систем, получаемых из этой элементарных ячеек, отличающихся друг от друга длиной
сторон и углами между ними. Но почему-то снова появляется число 7? За этим скрывается закономерность, порождающая эти
кристаллографические системы, или это случайность? В этих системах каждый кристалл характеризуется наличием
определенных осей симметрии.
Куб:
 Октаэдр:
Октаэдр:
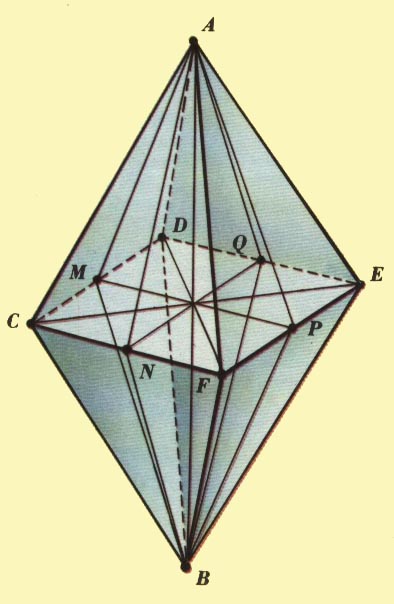
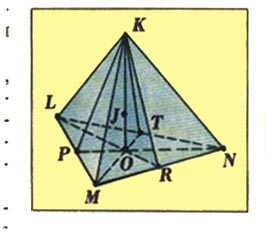 рис. 5
Из этих рисунков, характеризующих оси симметрии
в кристаллах, видно, что в той или тиной форме все кристаллические решетки
связаны с треугольными формами. На рисунке справа каждый квадрат (или в
общем случае, квадра) распадается на 4 триады. Поэтому каждая квадра имеет
ширину и высоту. Для квадрата ширина и высота квадры равны. На этом рисунке в
его центре просматривается и шестиугольник, собранный из треугольных форм. Рисунок справа говорит о том, что в таком кристалле ширина
не полная, характеризуя как бы незавершенность
структуры.
Специально следует отметить
кристаллы, имеющие кубическую структуру
рис. 5
Из этих рисунков, характеризующих оси симметрии
в кристаллах, видно, что в той или тиной форме все кристаллические решетки
связаны с треугольными формами. На рисунке справа каждый квадрат (или в
общем случае, квадра) распадается на 4 триады. Поэтому каждая квадра имеет
ширину и высоту. Для квадрата ширина и высота квадры равны. На этом рисунке в
его центре просматривается и шестиугольник, собранный из треугольных форм. Рисунок справа говорит о том, что в таком кристалле ширина
не полная, характеризуя как бы незавершенность
структуры.
Специально следует отметить
кристаллы, имеющие кубическую структуру
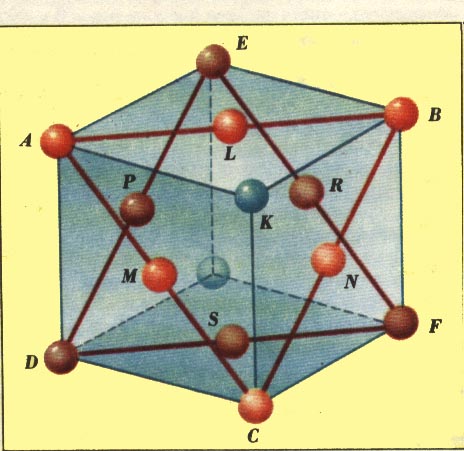 рис. 6
В этом рисунке, характеризующем
элементарную ячейку гранецентрированной кубической решетки в явном
виде выделяются две диагональные триады (DEF, ABC), а
четвертая диагональ характеризует ось симметрии (ось вращения) такой ячейки (ось
KS).
1.3. ТРИАНГУЛЯРЫ И КОРПУСКУЛЯРЫ
Вводимые ниже определения являются робкой
попыткой автора осознать простую истину из вышеизложенного материала, что все
монадные формы формируются из треугольников и четырехугольников и потому
этот факт может быть как-то зафиксирован, пусть даже на уровне
информацию для размышления, отражающей важнейшие специфические свойства
всех монадных форм.
Двойственность монадных форм (треугольники и квадраты)
позволяет ввести для них специальные
категории.
Триангула -
это треугольная монадная
форма.
Триангуляр - упорядоченная, замкнутая последовательность (сумма) триангул.
Триангуляр есть мера собственного пространства монадных форм триангульного
типа. Элеентарный триангуляо-трехугольная
пирамида.
Корпускула - это четырехгранная монадная форма.
Это битриангула. Корпускула допускает две основные формы. В одном случае она
получается путем последовательного склеивания односпиральных триангул по
граням. В результате такой склейки вторая триангулы будет сдвинута относительно
первой на 600.
В другом случае она формируется путем
антипаралельного склеивания разноспиральных триангул.
Корпускуляр - упорядоченная, замкнутая
последовательность(сумма) корпускул. Корпускуляр является мерой собственного
пространства корпускулярного типа. Это битриангуляр.
Он оже может иметь две формы. Одна форма образуется
путем последовательного соединения триангуляров, с одинаковой
спиральностью. Другая форма - путем антипаралельного склеивния разноспиральных
триангуляров.
Бикорпускуляр - склеивается из двух
битриангуляров, путем их последовательного, либо антипараллельного соединения.
При антипараллельном соединении мы получим совершенную
звезднотетраэдрическую монадную форму (или куб). При последовательном соединении
- четырехугольную пирамиду.
Данные монадные
формы определены с целью дать информации о возможных принципах формирования и
свойствах монадных кристаллов, в частности Платоновых
тел (рис.5).
рис. 6
В этом рисунке, характеризующем
элементарную ячейку гранецентрированной кубической решетки в явном
виде выделяются две диагональные триады (DEF, ABC), а
четвертая диагональ характеризует ось симметрии (ось вращения) такой ячейки (ось
KS).
1.3. ТРИАНГУЛЯРЫ И КОРПУСКУЛЯРЫ
Вводимые ниже определения являются робкой
попыткой автора осознать простую истину из вышеизложенного материала, что все
монадные формы формируются из треугольников и четырехугольников и потому
этот факт может быть как-то зафиксирован, пусть даже на уровне
информацию для размышления, отражающей важнейшие специфические свойства
всех монадных форм.
Двойственность монадных форм (треугольники и квадраты)
позволяет ввести для них специальные
категории.
Триангула -
это треугольная монадная
форма.
Триангуляр - упорядоченная, замкнутая последовательность (сумма) триангул.
Триангуляр есть мера собственного пространства монадных форм триангульного
типа. Элеентарный триангуляо-трехугольная
пирамида.
Корпускула - это четырехгранная монадная форма.
Это битриангула. Корпускула допускает две основные формы. В одном случае она
получается путем последовательного склеивания односпиральных триангул по
граням. В результате такой склейки вторая триангулы будет сдвинута относительно
первой на 600.
В другом случае она формируется путем
антипаралельного склеивания разноспиральных триангул.
Корпускуляр - упорядоченная, замкнутая
последовательность(сумма) корпускул. Корпускуляр является мерой собственного
пространства корпускулярного типа. Это битриангуляр.
Он оже может иметь две формы. Одна форма образуется
путем последовательного соединения триангуляров, с одинаковой
спиральностью. Другая форма - путем антипаралельного склеивния разноспиральных
триангуляров.
Бикорпускуляр - склеивается из двух
битриангуляров, путем их последовательного, либо антипараллельного соединения.
При антипараллельном соединении мы получим совершенную
звезднотетраэдрическую монадную форму (или куб). При последовательном соединении
- четырехугольную пирамиду.
Данные монадные
формы определены с целью дать информации о возможных принципах формирования и
свойствах монадных кристаллов, в частности Платоновых
тел (рис.5).
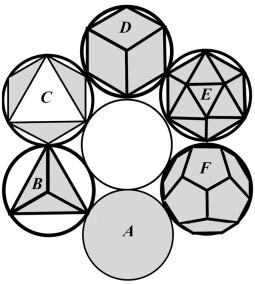 рис. 7
Из рисунка
видно, что эволюция Платоновых тел вначале осуществляется от сферы к
формированию триангуляров, затем рождается совершенная форма, но уже
корпускулярная монадная форма (куб), а далее эволюция снова возвращается к
битриангулярным формам.
путем эволюция которых завершается
формированием другой совершенной монадной формы - сферы.
Поскольку в гексаде эволюции сфера
и куб находятся на одной и той же оси, то будем считать, что сфера является
совершенной формой корпускуляра. Поэтому можно считать, что все эволюционные
процессы монадных форм будут направлены от одной корпускулярной формы к
другой, через упорядоченную последовательность триангулярных и
битриангулярных форм.
В связи с этим имеет
смысл данные противоположные друг другу корпускулярные формы называть
соответственно женскими и мужскими корпускулярами. В этом проявляется
дуадность корпускуляров. Будем считать сферу женским корпускуляром, а куб
-мужским.
Будем условно считать,
что эта та изначальная двойственная пара (монада), которая порождает монадный
мир (порождающая как пространство, так и энергию).
1.4. СТРЕЛЫ ОПТИМАЛЬНОСТИ или
ВЕКТОРЫ
УСТРЕМЛЕНИЙ
Поскольку
любой эволюционный процесс характеризуется определенной направленностью, то
можно считать, что любая монадная форма, любой монадный кристалл может быть
"соткан" из векторов. Так, при анализе свойств Единого закона, будет обосновано,
что на первом этапе эволюция направлена к формированию корпускулярных форм
со специфическим вектором устремлений, направленного
вовне пространства монадной формы. Второй этап эволюции монадных форм, от
корпускулярных монадных форм к триангулярным, наоборот, характеризуется
вектором устремлений, направленного вовнутрь монадной формы.
На следующих рисунках приведены примеры 4-х типов
триангул и корпускул. Желтые и голубые триангулы имеют
разную спиральность.
рис. 7
Из рисунка
видно, что эволюция Платоновых тел вначале осуществляется от сферы к
формированию триангуляров, затем рождается совершенная форма, но уже
корпускулярная монадная форма (куб), а далее эволюция снова возвращается к
битриангулярным формам.
путем эволюция которых завершается
формированием другой совершенной монадной формы - сферы.
Поскольку в гексаде эволюции сфера
и куб находятся на одной и той же оси, то будем считать, что сфера является
совершенной формой корпускуляра. Поэтому можно считать, что все эволюционные
процессы монадных форм будут направлены от одной корпускулярной формы к
другой, через упорядоченную последовательность триангулярных и
битриангулярных форм.
В связи с этим имеет
смысл данные противоположные друг другу корпускулярные формы называть
соответственно женскими и мужскими корпускулярами. В этом проявляется
дуадность корпускуляров. Будем считать сферу женским корпускуляром, а куб
-мужским.
Будем условно считать,
что эта та изначальная двойственная пара (монада), которая порождает монадный
мир (порождающая как пространство, так и энергию).
1.4. СТРЕЛЫ ОПТИМАЛЬНОСТИ или
ВЕКТОРЫ
УСТРЕМЛЕНИЙ
Поскольку
любой эволюционный процесс характеризуется определенной направленностью, то
можно считать, что любая монадная форма, любой монадный кристалл может быть
"соткан" из векторов. Так, при анализе свойств Единого закона, будет обосновано,
что на первом этапе эволюция направлена к формированию корпускулярных форм
со специфическим вектором устремлений, направленного
вовне пространства монадной формы. Второй этап эволюции монадных форм, от
корпускулярных монадных форм к триангулярным, наоборот, характеризуется
вектором устремлений, направленного вовнутрь монадной формы.
На следующих рисунках приведены примеры 4-х типов
триангул и корпускул. Желтые и голубые триангулы имеют
разную спиральность.
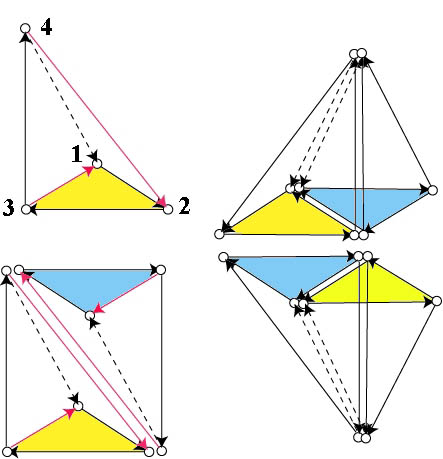 рис. 11
На данном рисунке вершины триангулятора <1,2,3,4> отражают последоватльнось
порождения триангулятора из триангул. Стрелки символизируют векторы
устремлений. Красные стрелки означают, что данный вектор устремлений не
является замкнутым для одной из граней триангулятора. Из рисунка видно, что
триангуляр является полностью уравновешенным монадным кристаллом. Так,
неуравновешенный в триангуле <1,2,4> вектор 4,2
оказывается уравновешен в триангуле <2,3,4>. То же самое можно сказать и про вектор устремлений 3,1. На других рисунках показаны примеры "склеек" уже триангуляров.
На рис. справа приведен пример недостроенного монадного кристалла.
Анализ Платоновых тел
показывает, что большинство этих монадных форм относятся к триангулярным.
Другими словами существование этих форм можно отождествить со свойствами
пространства, которое при отрицательном векторе устремлений является
расширяющимся, а при положительном векторе устремлений -
сжимающимся. Расширяющееся
пространство характеризуется увеличением "проявленной" массы, а сжимающееся - ее
уменьшением.
Триангулярный вектор устремлений обладает важным свойством. Зная
этот вектор мы однозначно можем с его вершины видеть все пространство, т.к. с
конца этого вектора оно будет видно как трехмерное. Другими словами конец
вектора устремления триангуляра будет всегда являться вершиной
тетраэдра. Отсюда вытекает важнейший вывод о трехмерности нашего
проявленного пространства, о трехмерности нашей Вселенной, о трехмерности
пространства монадных форм, о трехмерности Единого самосогласованного поля, о
трехмерности Единого Периодического закона.
Но какой же физический смысл
может быть заложен в корпускуляры?
Может быть корпускуляры связать
с энергией? Так, в силу
взаимодополнительности увеличение и уменьшение массы пространства напрямую
связаны с энергетикой. На первом этапе, как у маятника, происходит
увеличение трансформация потенциальной энергии в кинетическую, а на втором,
наоборот, кинетической в потенциальную.
Если триангулярный и
корпускулярный вектора устремлений будут перпендикулярны друг к другу, то
они могут взаимопревращаться друг в друга в процессе эволюции
монадной формы. Эти свойства могут порождать в монадных формах
различные типы полей, обладающих как потенциальной, так и кинетической
энергией.
Рассмотрим некоторые
специфичные свойства корпускуляров, на примере мужского корпускуляра. Монадная
форма такого корпускуляра является звездным тетраэдром (кубом). Она составлена
из двух триангулярных форм (тетраэдров), "склеенных" в единую форму. Но в
силу того, что векторы устремлений в каждом тетраэдре оказываются
противоположны, то такая склейка может выполняться таким образом, чтобы
суммарный вектор устремления звездного тетраэдра оказывался равным нулю.
Любое рассогласование векторов устремлений, выше определенного предела, в
"склеенных" тетраэдрах вызовет их расталкивание. Поскольку энергия
порождается женской формой корпускуляров, и снова поглощается этой же
формой.
В триангулах дело может
обстоять наоборот. После "склеивания" они стремятся к дальнейшему
присоединению и способствуют, тем самым, формированию массы, т.е. вектор
устремления массы стремится к центру масс.
Если сопоставить свойства данных типов монадных форм
(триангуляров и корпускуляров) и свойства типов элементарных частиц (бозоны и
фермионы), то невольно можно заметить между ними определенные аналогии. Трудно
сказать, случайность это, или совпадение, но свойства фермионов напоминают
свойства корпускуляров (в одном состоянии могут находиться только два фермиона с
противоположными спинами), а свойства бозонов напоминают
свойства триангул (в одном состоянии может находиться сколь угодно
много триангул). Из этих триангул можно "ткать нити", которые могут
сворачиваться в клубок.
Таковы
самые первые представления о пространстве и энергии монадных форм.
Только пространство и энергия (свет) являются той изначальной двойственной
парой, которая, собственно, является стоком и истоком эволюции любой
монадной формы. Заметим, что пространство и
энергия здесь никак не связаны со временем. Время
начинает проявляться тогда, когда появляется необходимость в синхронизации
подобных (триангулярных или корпускулярных) собственных пространств, когда
возникает необходимость инвариантных переходов из одного собственного
пространства монадных форм в другое.
2. КЛАССИФИКАЦИЯ
КРИСТАЛЛОВ
2.1.ТВЕРДЫЕ
КРИСТАЛЛЫ
Мир твердых кристаллов макромира чрезвычайно
многообразен и богат. Этот мир проявляется уже на уровне Периодической системы
химических элементов Д.И. Менделеева. Химикам известно, что каждый
химический элемент может иметь несколько форм, обладающих разными
химическими свойствами (изомеры- химические элементы, имеющие один и тот же
заряд ядра, но содержащих разное число нейтронов).
Оказывается, что изомеры могут иметь разные
структурные свойства, т.е. речь идет о химических элементах, имеющих совершенно один и тот же
состав, но обладающих разной внутренней структурой, как например, графит и
алмаз, обладают разной внутренней структурой. Подобные элементы академик Болотов
называет изостерами и приводит Периодическую таблицу химических элементов, как
некую периодизацию кристаллических элементов, в которой каждый химический
элемент имеет несколько изостеров.
1. Все изостеры одного и того же элемента
отличаются разной внутренней структурой, имеют разную "кристаллическую решетку".
2. Если в одном изостере нарушить хотя бы одну
связь в его "кристаллической решетке", то это может привести к измерению его
внутренней структуры и трансформацию в другой изостер.
3. Если в изостере изменить состав на 1
единицу, то изостер трансформируется в новый химический элемент с
соответствующей структурой "внутренней кристаллической решетки".
4. Все изостеры с одной
начальной структурой формируют единое периодическое подсемейство изостеров
химических элементов, т.е. Периодическая система химических элементов может
иметь несколько изостерных семейств Периодической системы химических элементов.
К такому выводу приводит закономерность о преемственности структуры изостерных
элементов. Спонтанные "мутации" приводят к изменению его внутренней структуры и
переход его в другое изостерное подсемейство.
Таким образом, изостеры
характеризуют многомерность даже в рамках одних и тех же химических элементов, с
одним и тем же количественным составом. Однако многие ученые не поняли смысл
открытия академика Б.В. Болотова, который вместо химического "элемента" ввел
понятие "изостер". Однако они и не отвергли это окрытие, возможно, потому,
что Б.В. Болотов к этому времени уже был академиком. А ведь это открытие можно
смело считать реформой Периодической системы химических элементов. Увы, этого не
произошло. Жаль, что это не известно широкому научному кругу.
Еще более жаль, что этот замечательный ученый и изобретатель уже ушел в мир
иной, так и не оцененный по достоинству за это поистине великое
открытие.
Но если химические
элементы обладают кристаллической решеткой, то они могут формировать, по образу
и подобию многомерные кристаллические решетки высших измерений, порождая мир
кристаллических форм.
рис. 11
На данном рисунке вершины триангулятора <1,2,3,4> отражают последоватльнось
порождения триангулятора из триангул. Стрелки символизируют векторы
устремлений. Красные стрелки означают, что данный вектор устремлений не
является замкнутым для одной из граней триангулятора. Из рисунка видно, что
триангуляр является полностью уравновешенным монадным кристаллом. Так,
неуравновешенный в триангуле <1,2,4> вектор 4,2
оказывается уравновешен в триангуле <2,3,4>. То же самое можно сказать и про вектор устремлений 3,1. На других рисунках показаны примеры "склеек" уже триангуляров.
На рис. справа приведен пример недостроенного монадного кристалла.
Анализ Платоновых тел
показывает, что большинство этих монадных форм относятся к триангулярным.
Другими словами существование этих форм можно отождествить со свойствами
пространства, которое при отрицательном векторе устремлений является
расширяющимся, а при положительном векторе устремлений -
сжимающимся. Расширяющееся
пространство характеризуется увеличением "проявленной" массы, а сжимающееся - ее
уменьшением.
Триангулярный вектор устремлений обладает важным свойством. Зная
этот вектор мы однозначно можем с его вершины видеть все пространство, т.к. с
конца этого вектора оно будет видно как трехмерное. Другими словами конец
вектора устремления триангуляра будет всегда являться вершиной
тетраэдра. Отсюда вытекает важнейший вывод о трехмерности нашего
проявленного пространства, о трехмерности нашей Вселенной, о трехмерности
пространства монадных форм, о трехмерности Единого самосогласованного поля, о
трехмерности Единого Периодического закона.
Но какой же физический смысл
может быть заложен в корпускуляры?
Может быть корпускуляры связать
с энергией? Так, в силу
взаимодополнительности увеличение и уменьшение массы пространства напрямую
связаны с энергетикой. На первом этапе, как у маятника, происходит
увеличение трансформация потенциальной энергии в кинетическую, а на втором,
наоборот, кинетической в потенциальную.
Если триангулярный и
корпускулярный вектора устремлений будут перпендикулярны друг к другу, то
они могут взаимопревращаться друг в друга в процессе эволюции
монадной формы. Эти свойства могут порождать в монадных формах
различные типы полей, обладающих как потенциальной, так и кинетической
энергией.
Рассмотрим некоторые
специфичные свойства корпускуляров, на примере мужского корпускуляра. Монадная
форма такого корпускуляра является звездным тетраэдром (кубом). Она составлена
из двух триангулярных форм (тетраэдров), "склеенных" в единую форму. Но в
силу того, что векторы устремлений в каждом тетраэдре оказываются
противоположны, то такая склейка может выполняться таким образом, чтобы
суммарный вектор устремления звездного тетраэдра оказывался равным нулю.
Любое рассогласование векторов устремлений, выше определенного предела, в
"склеенных" тетраэдрах вызовет их расталкивание. Поскольку энергия
порождается женской формой корпускуляров, и снова поглощается этой же
формой.
В триангулах дело может
обстоять наоборот. После "склеивания" они стремятся к дальнейшему
присоединению и способствуют, тем самым, формированию массы, т.е. вектор
устремления массы стремится к центру масс.
Если сопоставить свойства данных типов монадных форм
(триангуляров и корпускуляров) и свойства типов элементарных частиц (бозоны и
фермионы), то невольно можно заметить между ними определенные аналогии. Трудно
сказать, случайность это, или совпадение, но свойства фермионов напоминают
свойства корпускуляров (в одном состоянии могут находиться только два фермиона с
противоположными спинами), а свойства бозонов напоминают
свойства триангул (в одном состоянии может находиться сколь угодно
много триангул). Из этих триангул можно "ткать нити", которые могут
сворачиваться в клубок.
Таковы
самые первые представления о пространстве и энергии монадных форм.
Только пространство и энергия (свет) являются той изначальной двойственной
парой, которая, собственно, является стоком и истоком эволюции любой
монадной формы. Заметим, что пространство и
энергия здесь никак не связаны со временем. Время
начинает проявляться тогда, когда появляется необходимость в синхронизации
подобных (триангулярных или корпускулярных) собственных пространств, когда
возникает необходимость инвариантных переходов из одного собственного
пространства монадных форм в другое.
2. КЛАССИФИКАЦИЯ
КРИСТАЛЛОВ
2.1.ТВЕРДЫЕ
КРИСТАЛЛЫ
Мир твердых кристаллов макромира чрезвычайно
многообразен и богат. Этот мир проявляется уже на уровне Периодической системы
химических элементов Д.И. Менделеева. Химикам известно, что каждый
химический элемент может иметь несколько форм, обладающих разными
химическими свойствами (изомеры- химические элементы, имеющие один и тот же
заряд ядра, но содержащих разное число нейтронов).
Оказывается, что изомеры могут иметь разные
структурные свойства, т.е. речь идет о химических элементах, имеющих совершенно один и тот же
состав, но обладающих разной внутренней структурой, как например, графит и
алмаз, обладают разной внутренней структурой. Подобные элементы академик Болотов
называет изостерами и приводит Периодическую таблицу химических элементов, как
некую периодизацию кристаллических элементов, в которой каждый химический
элемент имеет несколько изостеров.
1. Все изостеры одного и того же элемента
отличаются разной внутренней структурой, имеют разную "кристаллическую решетку".
2. Если в одном изостере нарушить хотя бы одну
связь в его "кристаллической решетке", то это может привести к измерению его
внутренней структуры и трансформацию в другой изостер.
3. Если в изостере изменить состав на 1
единицу, то изостер трансформируется в новый химический элемент с
соответствующей структурой "внутренней кристаллической решетки".
4. Все изостеры с одной
начальной структурой формируют единое периодическое подсемейство изостеров
химических элементов, т.е. Периодическая система химических элементов может
иметь несколько изостерных семейств Периодической системы химических элементов.
К такому выводу приводит закономерность о преемственности структуры изостерных
элементов. Спонтанные "мутации" приводят к изменению его внутренней структуры и
переход его в другое изостерное подсемейство.
Таким образом, изостеры
характеризуют многомерность даже в рамках одних и тех же химических элементов, с
одним и тем же количественным составом. Однако многие ученые не поняли смысл
открытия академика Б.В. Болотова, который вместо химического "элемента" ввел
понятие "изостер". Однако они и не отвергли это окрытие, возможно, потому,
что Б.В. Болотов к этому времени уже был академиком. А ведь это открытие можно
смело считать реформой Периодической системы химических элементов. Увы, этого не
произошло. Жаль, что это не известно широкому научному кругу.
Еще более жаль, что этот замечательный ученый и изобретатель уже ушел в мир
иной, так и не оцененный по достоинству за это поистине великое
открытие.
Но если химические
элементы обладают кристаллической решеткой, то они могут формировать, по образу
и подобию многомерные кристаллические решетки высших измерений, порождая мир
кристаллических форм.

 рис. 12
И весь этот сказочно богатый
мир кристаллов сложен в конечном итоге из треугольников и
четырехугольников.
Но в конечном итоге
весь этот бесконечно многообразный мир кристаллов состоит всего лишь из двух
взаимодополнительных групп, отражающих янский, или
иньский аспект
рис. 12
И весь этот сказочно богатый
мир кристаллов сложен в конечном итоге из треугольников и
четырехугольников.
Но в конечном итоге
весь этот бесконечно многообразный мир кристаллов состоит всего лишь из двух
взаимодополнительных групп, отражающих янский, или
иньский аспект
 Иньские кристаллы не имеют
"шипов". Их грани формируются пирамидами, все вершины которых совмещены в центре
кристалла. Янские кристаллы формируются уже удвоенными пирамидами, одна вершина
которой находится в центре кристалла, а другая формирует "шип"
кристалла.
В этой связи особый интерес для нас
представляет звездный тетраэдр
Иньские кристаллы не имеют
"шипов". Их грани формируются пирамидами, все вершины которых совмещены в центре
кристалла. Янские кристаллы формируются уже удвоенными пирамидами, одна вершина
которой находится в центре кристалла, а другая формирует "шип"
кристалла.
В этой связи особый интерес для нас
представляет звездный тетраэдр
 Это янский кристалл, которому соответствует женский
кристалл -октаэдр.
Выражая отношения между октаэдром и звездным
тетраэдром через отношения "число вершин /число граней", получим следующее
тождество,
Это янский кристалл, которому соответствует женский
кристалл -октаэдр.
Выражая отношения между октаэдром и звездным
тетраэдром через отношения "число вершин /число граней", получим следующее
тождество,
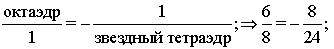 ,
отражающего отношения между мужским и женским началом
в этих кристаллах.
Но выше мы уже говорили о том, что куб и октаэдр
взаимодополнительны и эта взаимодополнительность может быть отражена
тождеством
,
отражающего отношения между мужским и женским началом
в этих кристаллах.
Но выше мы уже говорили о том, что куб и октаэдр
взаимодополнительны и эта взаимодополнительность может быть отражена
тождеством
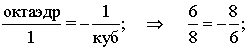 Таким образом, использование вышеприведенных
тождеств позволяет проводить классификацию кристаллов с позиций природных
операционных механизмов Единого закона эволюции двойственных
отношений.
2.2. ЖИДКИЕ
КРИСТАЛЛЫ
Жидкий кристалл - это особое состояние вещества, промежуточное между жидким
и твердым состояниями. В жидкости молекулы могут свободно
вращаться и перемещаться в любых направлениях. В кристаллическом твердом теле
они расположены по узлам правильной геометрической сетки, называемой
кристаллической решеткой, и могут лишь вращаться в своих фиксированных позициях.
В жидком кристалле имеется некоторая степень геометрической упорядоченности в
расположении молекул, но допускается и некоторая свобода перемещения.
Считается, что состояние жидкого кристалла открыл в 1888 австрийский ботаник
Ф.Рейнитцер. Он изучал поведение органического твердого вещества, называемого
холестерилбензоатом. При нагревании это соединение переходило из твердого в
мутное на вид состояние, ныне называемое жидкокристаллическим, а затем в
прозрачную жидкость; при охлаждении последовательность превращений повторялась в
обратном порядке. Рейнитцер отметил также, что при нагревании изменяется цвет
жидкого кристалла – от красного к синему, с повторением в обратном порядке при
охлаждении. Почти все жидкие кристаллы, обнаруженные на сегодняшний день,
представляют собой органические соединения; примерно 50% всех известных
органических соединений при нагревании образуют жидкие кристаллы. В литературе
описаны также жидкие кристаллы некоторых гидроксидов (например, Fe2O3ЧxH2O).
Консистенция жидких кристаллов может быть разной – от легкотекучей жидкой до
пастообразной. Жидкие кристаллы имеют необычные оптические свойства, что
используется в технике.
Известно,
что при нагревании некоторых твердых органических соединений их кристаллическая
решетка разваливается и образуется жидкий кристалл. Если температуру повышать и
далее, то жидкий кристалл переходит в настоящую жидкость. Жидкие кристаллы,
образующиеся при нагревании, называются термотропными. В конце 1960-х годов были получены
органические соединения, являющиеся жидкокристаллическими при комнатной
температуре.
Но существует и
другой способ получения жидких кристаллов – обработка некоторых соединений
контролируемым количеством воды или другого полярного растворителя. (Полярным
называется растворитель, состоящий из молекул-диполей, на одном конце которых
находится положительный электрический заряд, а на другом – отрицательный.)
Жидкие кристаллы, состоящие из двух и более компонентов, называются лиотропными. Их можно получать, смешивая с водой
такие материалы, как мыла, детергенты, полипептиды, жирные кислоты, соли жирных
кислот и фосфолипиды.
Жидкие кристаллы образуются из молекул, имеющих разную геометрическую форму
(чаще всего – удлиненных или дискообразных). Электрическими межмолекулярными
силами определяется характер «упаковки» молекул, т.е. то, как они геометрически
соотносятся друг с другом.
Расположение молекул в жидких
кристаллах изменяется под действием таких факторов, как температура, давление,
электрические и магнитные поля; изменения же расположения молекул приводят к
изменению оптических свойств, таких, как цвет, прозрачность и способность к
вращению плоскости поляризации проходящего света. На всем этом основаны
многочисленные применения жидких кристаллов.
Так, жидкие кристаллы широко применяются
в производстве наручных часов и небольших калькуляторов. Создаются плоские
телевизоры с тонким жидкокристаллическим экраном, и т.д..
И хотя для жидких кристаллов отсутствуют такая же подробная классификация, как
для твердых кристаллов, однако, в соответствии с природными операционными
механизмами Единого закона можно смело выдвинуть гипотезу о том, что мир жидких
кристаллов столь же богат и разнообразен, как и мир тверддых
кристаллов.
Таким образом, использование вышеприведенных
тождеств позволяет проводить классификацию кристаллов с позиций природных
операционных механизмов Единого закона эволюции двойственных
отношений.
2.2. ЖИДКИЕ
КРИСТАЛЛЫ
Жидкий кристалл - это особое состояние вещества, промежуточное между жидким
и твердым состояниями. В жидкости молекулы могут свободно
вращаться и перемещаться в любых направлениях. В кристаллическом твердом теле
они расположены по узлам правильной геометрической сетки, называемой
кристаллической решеткой, и могут лишь вращаться в своих фиксированных позициях.
В жидком кристалле имеется некоторая степень геометрической упорядоченности в
расположении молекул, но допускается и некоторая свобода перемещения.
Считается, что состояние жидкого кристалла открыл в 1888 австрийский ботаник
Ф.Рейнитцер. Он изучал поведение органического твердого вещества, называемого
холестерилбензоатом. При нагревании это соединение переходило из твердого в
мутное на вид состояние, ныне называемое жидкокристаллическим, а затем в
прозрачную жидкость; при охлаждении последовательность превращений повторялась в
обратном порядке. Рейнитцер отметил также, что при нагревании изменяется цвет
жидкого кристалла – от красного к синему, с повторением в обратном порядке при
охлаждении. Почти все жидкие кристаллы, обнаруженные на сегодняшний день,
представляют собой органические соединения; примерно 50% всех известных
органических соединений при нагревании образуют жидкие кристаллы. В литературе
описаны также жидкие кристаллы некоторых гидроксидов (например, Fe2O3ЧxH2O).
Консистенция жидких кристаллов может быть разной – от легкотекучей жидкой до
пастообразной. Жидкие кристаллы имеют необычные оптические свойства, что
используется в технике.
Известно,
что при нагревании некоторых твердых органических соединений их кристаллическая
решетка разваливается и образуется жидкий кристалл. Если температуру повышать и
далее, то жидкий кристалл переходит в настоящую жидкость. Жидкие кристаллы,
образующиеся при нагревании, называются термотропными. В конце 1960-х годов были получены
органические соединения, являющиеся жидкокристаллическими при комнатной
температуре.
Но существует и
другой способ получения жидких кристаллов – обработка некоторых соединений
контролируемым количеством воды или другого полярного растворителя. (Полярным
называется растворитель, состоящий из молекул-диполей, на одном конце которых
находится положительный электрический заряд, а на другом – отрицательный.)
Жидкие кристаллы, состоящие из двух и более компонентов, называются лиотропными. Их можно получать, смешивая с водой
такие материалы, как мыла, детергенты, полипептиды, жирные кислоты, соли жирных
кислот и фосфолипиды.
Жидкие кристаллы образуются из молекул, имеющих разную геометрическую форму
(чаще всего – удлиненных или дискообразных). Электрическими межмолекулярными
силами определяется характер «упаковки» молекул, т.е. то, как они геометрически
соотносятся друг с другом.
Расположение молекул в жидких
кристаллах изменяется под действием таких факторов, как температура, давление,
электрические и магнитные поля; изменения же расположения молекул приводят к
изменению оптических свойств, таких, как цвет, прозрачность и способность к
вращению плоскости поляризации проходящего света. На всем этом основаны
многочисленные применения жидких кристаллов.
Так, жидкие кристаллы широко применяются
в производстве наручных часов и небольших калькуляторов. Создаются плоские
телевизоры с тонким жидкокристаллическим экраном, и т.д..
И хотя для жидких кристаллов отсутствуют такая же подробная классификация, как
для твердых кристаллов, однако, в соответствии с природными операционными
механизмами Единого закона можно смело выдвинуть гипотезу о том, что мир жидких
кристаллов столь же богат и разнообразен, как и мир тверддых
кристаллов.
2.3. ПЛАЗМЕННЫЕ КРИСТАЛЛЫ В своей книге "Теория кристаллизации плазмы" Владимир Тимофеевич Гринев( diplazmv56@mail.ru) пишет о том, что вот уже 20 лет существует настоящее фундаментальное открытие, способное инициировать фейерверк фантастических изобретений, и способное в полной мере удовлетворить самые смелые ожидания. Его основная суть в том, что удалось разгадать свойства вещества при температурах в сотни миллионов градусов. "По существу, открыто принципиально новое, пятое состояние вещества. Ему дано условное название "ПЛАЗМЕННЫЙ КРИСТАЛЛ" (ПК) или "КРИСТАЛЛИЧЕСКАЯ ПЛАЗМА". Как оказалось, при очень высокой температуре вещество, уже, не может находиться в состоянии плазмы, и самопроизвольно, скачкообразно, переходит в принципиально иное состояние. Поняты основные причины и законы этого перехода. Выяснены основные свойства вещества в этом состоянии. Обнаружено множество уже существующих и широко известных экспериментальных фактов прямо подтверждающих существование вышеназванного состояния вещества. Более того - найдены решения, позволяющие получать ПК в лаборатории. Как выяснилось, ПК обладают многими фантастическими свойствами. Например, их совершенно не нужно удерживать, как пытаются удержать плазму. При остывании ПК лавинообразно переходит в состояние обычной плазмы и взрывается, как взрывается шаровая молния. В принципе, шаровая молния это и есть кусочек вещества в пятом состоянии. ПК (шаровые молнии) могут использоваться как реакторы управляемого ядерного синтеза, как установки управляемой мутации химических элементов - из водорода можно получать в промышленных масштабах любой химический элемент, от гелия до урана и золота. При этом, термоядерные реакторы на ПК это относительно простые, надежные, недорогие устройства, совершенно непохожие на современные установки, работающие по совершенно по другому принципу, абсолютно безопасные в эксплуатации, не нарабатывающие радиоактивные отходы, обеспечивающие прямое преобразование энергии ядерного синтеза в электрическую и способные использовать в качестве топлива не только дейтерий и тритий, но и множество других химических элементов. ПК могут быть использованы как генераторы сверхмощного когерентного излучения в любом диапазоне, от радиоволн до жесткого ядерного излучения (рентгеновский лазер например), и как сверхчувствительные радиоприемники того же диапазона". В моих монографиях [1] и [2] приводятся другие дополнительные обоснования свойств плазменных кристаллов. В соответствии с едиными природными операционными принципами Единого закона эволюции двойственных отношений были приведены свойства "горячих", поистине звездной Периодической системе элементов - астроноидов еще в 1999 году. Кроме того, информация о свойствах этих поистине звездных кристаллов приводится и на страницах данного сайта (О космологии). Но кто из ученых заинтересовался данными публикациями? Никто! Разве может "серьмяжный мужик" написать что-то такое, что их благородиям не известно? А потому их вывод однозначен -лжеистина. 2.4. ВОЛНОВЫЕ КРИСТАЛЛЫ Современная наука уже имеет достаточно хорошие представления и о свойствах кристаллов совершенно иного уровня - волновых кристаллов. Эти кристаллы также, по образу и подобию порождаются природными операционными механизмами Единого закона. Об этом свидетельствуют публикации П.Гаряева (Волновой генетический код), И.И. Дороднова (Дороднов И.И. ) и других авторов. Уже существуют практические доказательства существования волнового уравнения Единого закона (Волновой геном), формирующего двойные спирали волновых функций. Известно, что волны любой природы характеризуются длиной волны (l) и ее периодом (t),а их взаимодействие описывается в рамках передатчика (прд) и приемника (прм) волнового излучения, которые могут двигаться друг относительно друга.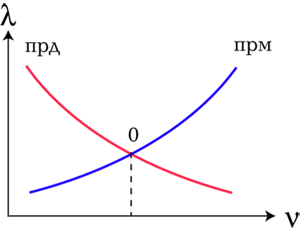 рис. 13
Подобное взаимодействие порождает весы монады
рис. 13
Подобное взаимодействие порождает весы монады
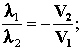 При движении приемника и
передатчика с одной и той же скоростью, в одном и том же направлении,
длина волны остается неизменной (равновесное
состояние).
При увеличении скорости движения передатчика в
направлении движения волны, длина волны уменьшается. При увеличении скорости
приемника волны (навстречу фронту волны) соответственно уменьшается длина
принимаемой волны. И это наглядно видно из
тождества.
Более наглядно смысл этого тождества можно получить
из следующего рисунка
При движении приемника и
передатчика с одной и той же скоростью, в одном и том же направлении,
длина волны остается неизменной (равновесное
состояние).
При увеличении скорости движения передатчика в
направлении движения волны, длина волны уменьшается. При увеличении скорости
приемника волны (навстречу фронту волны) соответственно уменьшается длина
принимаемой волны. И это наглядно видно из
тождества.
Более наглядно смысл этого тождества можно получить
из следующего рисунка
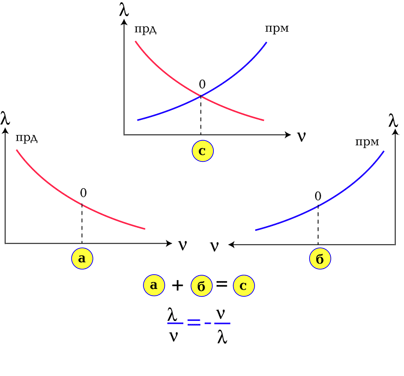 рис. 14
Видите, как естественно волновые весы монады
порождают равновесные состояния, в которых нет волны?
Многомерный характер весов монады порождает
многомерную волновую "кристаллическую решетку".
рис. 14
Видите, как естественно волновые весы монады
порождают равновесные состояния, в которых нет волны?
Многомерный характер весов монады порождает
многомерную волновую "кристаллическую решетку".
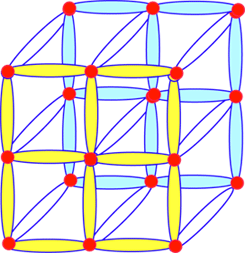 рис. 15
И мы
возвращаемся в лоно природных операционных механизмов Единого закона
эволюции двойственного отношения. Из этого кубика более наглядно
модно представить себе, что "дефекты" двойственного отношения вида
рис. 15
И мы
возвращаемся в лоно природных операционных механизмов Единого закона
эволюции двойственного отношения. Из этого кубика более наглядно
модно представить себе, что "дефекты" двойственного отношения вида
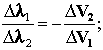 не могут не порождать сжатия (растяжения) структуры
волнового кубика, и могут вызывать преобразование физических размеров всего
"кубика", а не только и исключительно, длины, ширины, высоты, времени, длины
волны, периода и других волновых характеристик.
Кристаллическая решетка формируется природными операционными механизмами Единого
закона эволюции двойственного отношения и потому она проявляется во всех земных
и небесных сферах.
Корпускулярно-волновое единство структуры и функции,
частицы и волны наиболее ярко проявляются в Периодической системе химических
элементов.
не могут не порождать сжатия (растяжения) структуры
волнового кубика, и могут вызывать преобразование физических размеров всего
"кубика", а не только и исключительно, длины, ширины, высоты, времени, длины
волны, периода и других волновых характеристик.
Кристаллическая решетка формируется природными операционными механизмами Единого
закона эволюции двойственного отношения и потому она проявляется во всех земных
и небесных сферах.
Корпускулярно-волновое единство структуры и функции,
частицы и волны наиболее ярко проявляются в Периодической системе химических
элементов.
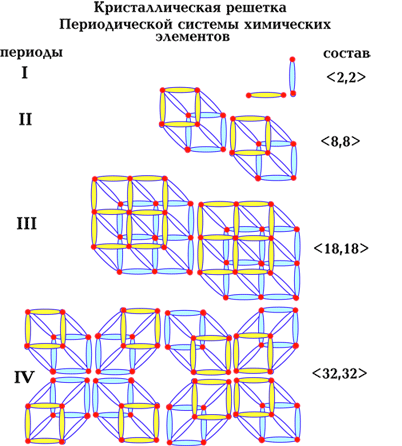 рис. 16
Данный рисунок представляет
собой двойную спираль "волновых кубиков" Периодической системы химических элементов. Эта структура
отражает собой совокупность полностью заполненных кристаллических оболочек (и
подоболочек) Периодической системы химических
элементов.
И хотя эта структура
является гипотетичной и ее еще долго не будут замечать в упор, но эта гипотеза
основывается на природных операционных принципах Единого
закона.
Посмотрите, как естественно в IV периоде из волновых кубиков
формируется ГиперКуб.
Как здесь снова не вспомнить библию "И последний
становится Первым". Может быть, кому то мои восклицания по данному поводу уже
"набили оскомину", но я прошу меня простить за эти и иные повторы,
которые я постоянно использую на разных страницах, но ... "повторение-мать
учения".
Посмотрите, IV период полностью соответствует свойствам матрицы И-Цзин (Книга
перемен).
рис. 16
Данный рисунок представляет
собой двойную спираль "волновых кубиков" Периодической системы химических элементов. Эта структура
отражает собой совокупность полностью заполненных кристаллических оболочек (и
подоболочек) Периодической системы химических
элементов.
И хотя эта структура
является гипотетичной и ее еще долго не будут замечать в упор, но эта гипотеза
основывается на природных операционных принципах Единого
закона.
Посмотрите, как естественно в IV периоде из волновых кубиков
формируется ГиперКуб.
Как здесь снова не вспомнить библию "И последний
становится Первым". Может быть, кому то мои восклицания по данному поводу уже
"набили оскомину", но я прошу меня простить за эти и иные повторы,
которые я постоянно использую на разных страницах, но ... "повторение-мать
учения".
Посмотрите, IV период полностью соответствует свойствам матрицы И-Цзин (Книга
перемен).
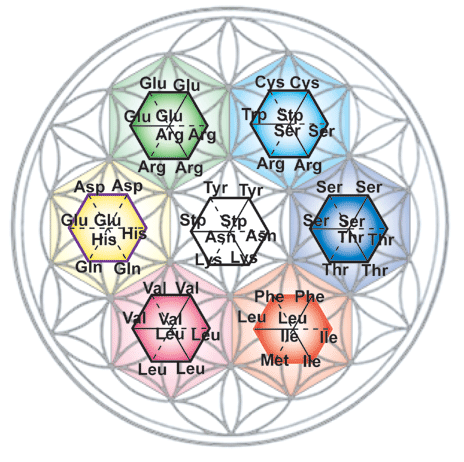
рис. 17
Данный рисунок
также приводится на многих страницах моего сайта. Он представляет собой
ГиперКуб генетического кода(О
генетическом коде)., наложенного на Древний Цветок Жизни (Эзотерика), который
содержит в себе все законы мироздания, все формулы, все до
единой. И на странице "Метагенетика" этому "наглому" утверждению древних
милогия дает современное обоснование.
Хотелось бы
обратить внимание читателей на следующие особенности рисунка Древнего цветка
Жизни. Он соткан из полуволн и представляет собой проекцию некоторого
пространственного совершенного кристалла на плоскость.
Прежде всего
обратим внимание, что в проекции мы видим только 7 "кубиков". Первый и Последний
кубик проектируются в один и тот же лепесток Цветка. На странице "Эзотерика"мы подробно
рассматривали свойства Древнего Цветка Жизни и говорили о том, что Цветок Жизни
содержит ровно 19 "волновых узлов".
А теперь взгляните на
структуру III периода
(рис.16) и увидьте, что этот рисунок состоит из двух 18 -ти узловых
кристаллических решеток, которые не могу не иметь Великого Предела -19-го узла.
Этот Предел соответствует химическому элементу с номером 57, который
является общим для всей структуры и соответствует группе химических
элементов(58-71), лантаноиды). Следующая группа
химических элементов начинается с номера (57+32=89). Этот элемент порождает
взаимодополнительную группу -лантаноидов (90-103
элементы).
Как видим, "волновые
кубики" Периодической системы химических элементов могут дать дополнительную
информацию о корпускулярных и волновых свойствах Периодической системы
химических элементов.
 а) химическая формула;
б) структурная формула;
в) реальная схема молекулы;
г) пространственное расположение атомов в
молекуле.
Из последней схемы видно, что в молекуле
метана каждая вершина может быть вершиной
тетраэдра.
Тетраэдр является
основой совершенных форм кристаллов нашего мироздания. Кроме того, из этих
схем непосредственно видно, что "четыре стихии" порождаются "Пятой стихией". И
это не случайно (Пирамида
Силы). Эволюция монадных форм все свои творения порождает по образу и
подобию, используя природные операционные механизмы Единого
закона.
Хотелось бы отметить
также смешанные монадные форму, одной из которых является кубоктаэдр
(рис.1).
а) химическая формула;
б) структурная формула;
в) реальная схема молекулы;
г) пространственное расположение атомов в
молекуле.
Из последней схемы видно, что в молекуле
метана каждая вершина может быть вершиной
тетраэдра.
Тетраэдр является
основой совершенных форм кристаллов нашего мироздания. Кроме того, из этих
схем непосредственно видно, что "четыре стихии" порождаются "Пятой стихией". И
это не случайно (Пирамида
Силы). Эволюция монадных форм все свои творения порождает по образу и
подобию, используя природные операционные механизмы Единого
закона.
Хотелось бы отметить
также смешанные монадные форму, одной из которых является кубоктаэдр
(рис.1).
Рис.1 Можно с одинаковым основанием считать эту фигуру усеченным кубом или октаэдром. Бакминстер Фуллер, обнаруживший этот многогранник, считал, что он является величайшей из всех форм творения. Для него этот многогранник был так важен, что он присвоил ему совершенно новое имя - векторное равновесие. Ниже мы увидим, что такое название чрезвычайно актуально, т.к. свойства всех кристаллов будут определяться именно их внутренними векторными свойствами. Он открыл, что эта форма, через разные формы вращения, превращается во все пять Платоновых тел. Кажется, что эта форма содержит их все внутри себя. Двойником кубоктаэдра является ромбододэкаэдр, который получается путем соединения центров кубоктаэдра (и наоборот). Д. Мельхиседек пишет об этом следующим образом (т.1, стр. 194): "Я думаю, что первые пять Платоновых тел - это первые пять нот пентатоники. В октаве 7 нот, последние две относятся к кубоктаэдру и ромбодекаэдру". Видимо, не будет преувеличением сказать, что и остальные пять дополнительных монадных форм, которые образуют целостную хроматическую монадную гамму многогранников, и будут содержать в качестве граней только треугольники и (или) квадраты. Следовательно, мир кристаллов сложен из треугольных, или квадратных граней. О мире кристаллов написано много замечательных книг. И это не удивительно. Мир кристаллов вездесущ. Он также, как и мир волн, пронизывает все явления нашей жизни. Этот мир целиком и полностью соткан из мира симметрии и асимметрии. Он проявляется себя в живой и неживой материи. Мир элементарных частиц, атомы химических элементов, молекулы, минералы, флора и фауна планеты-все это кристаллические структуры. Так, например, в мире органической химии можно вспомнить о молекуле бензоле (С6H6). Атомы углерода располагаются в одной плоскости, образуя правильный шестиугольник.

 Рис. 2
Рис. 3
На первый взгляд такая структура не
должна быть симметричной, т.к. молекулы углерода в бензольном кольце
связаны не одинаковыми связями (одинарными и двойными). Это должно
искажать структуру кольца. Но этого не происходит. Коррекция формы
осуществляется на следующем "этаже", за счет обобществления бензольным кольцом
шести электронов, не занятых в локализованных связях между атомами, а способных
свободно перемещаться по бензольному кольцу, как бы демонстрируя наличие некой
силовой линии в кристалле (рис. 3). Штриховые линии обозначают наличие не
локализованной связи, возникающие за счет обобществления шести электронов.
Почему они обобществляются? Почему возникают подобные
силовые линии?
Но разные кристаллы не обязательно
формируются разными элементами. Пример, алмаз и графит. Различие в их
свойствах связано исключительно с различием их кристаллической
структуры. Кристаллическая решетка, обратите внимание, представляет собой
природный трехмерный орнамент. Заметим также, что всего существует
семь типов симметрии повторяющихся рисунков в орнаменте, которые носят
название бордюров. Можно ли сказать, что это тоже случайность, или совпадение
?
Рис. 2
Рис. 3
На первый взгляд такая структура не
должна быть симметричной, т.к. молекулы углерода в бензольном кольце
связаны не одинаковыми связями (одинарными и двойными). Это должно
искажать структуру кольца. Но этого не происходит. Коррекция формы
осуществляется на следующем "этаже", за счет обобществления бензольным кольцом
шести электронов, не занятых в локализованных связях между атомами, а способных
свободно перемещаться по бензольному кольцу, как бы демонстрируя наличие некой
силовой линии в кристалле (рис. 3). Штриховые линии обозначают наличие не
локализованной связи, возникающие за счет обобществления шести электронов.
Почему они обобществляются? Почему возникают подобные
силовые линии?
Но разные кристаллы не обязательно
формируются разными элементами. Пример, алмаз и графит. Различие в их
свойствах связано исключительно с различием их кристаллической
структуры. Кристаллическая решетка, обратите внимание, представляет собой
природный трехмерный орнамент. Заметим также, что всего существует
семь типов симметрии повторяющихся рисунков в орнаменте, которые носят
название бордюров. Можно ли сказать, что это тоже случайность, или совпадение
?
 рис. 4
Здесь a, b,c,
длины ребер элементарной ячейки, а
рис. 4
Здесь a, b,c,
длины ребер элементарной ячейки, а  Октаэдр:
Октаэдр:

 рис. 5
Из этих рисунков, характеризующих оси симметрии
в кристаллах, видно, что в той или тиной форме все кристаллические решетки
связаны с треугольными формами. На рисунке справа каждый квадрат (или в
общем случае, квадра) распадается на 4 триады. Поэтому каждая квадра имеет
ширину и высоту. Для квадрата ширина и высота квадры равны. На этом рисунке в
его центре просматривается и шестиугольник, собранный из треугольных форм. Рисунок справа говорит о том, что в таком кристалле ширина
не полная, характеризуя как бы незавершенность
структуры.
Специально следует отметить
кристаллы, имеющие кубическую структуру
рис. 5
Из этих рисунков, характеризующих оси симметрии
в кристаллах, видно, что в той или тиной форме все кристаллические решетки
связаны с треугольными формами. На рисунке справа каждый квадрат (или в
общем случае, квадра) распадается на 4 триады. Поэтому каждая квадра имеет
ширину и высоту. Для квадрата ширина и высота квадры равны. На этом рисунке в
его центре просматривается и шестиугольник, собранный из треугольных форм. Рисунок справа говорит о том, что в таком кристалле ширина
не полная, характеризуя как бы незавершенность
структуры.
Специально следует отметить
кристаллы, имеющие кубическую структуру
 рис. 6
В этом рисунке, характеризующем
элементарную ячейку гранецентрированной кубической решетки в явном
виде выделяются две диагональные триады (DEF, ABC), а
четвертая диагональ характеризует ось симметрии (ось вращения) такой ячейки (ось
KS).
1.3. ТРИАНГУЛЯРЫ И КОРПУСКУЛЯРЫ
Вводимые ниже определения являются робкой
попыткой автора осознать простую истину из вышеизложенного материала, что все
монадные формы формируются из треугольников и четырехугольников и потому
этот факт может быть как-то зафиксирован, пусть даже на уровне
информацию для размышления, отражающей важнейшие специфические свойства
всех монадных форм.
Двойственность монадных форм (треугольники и квадраты)
позволяет ввести для них специальные
категории.
Триангула -
это треугольная монадная
форма.
Триангуляр - упорядоченная, замкнутая последовательность (сумма) триангул.
Триангуляр есть мера собственного пространства монадных форм триангульного
типа. Элеентарный триангуляо-трехугольная
пирамида.
Корпускула - это четырехгранная монадная форма.
Это битриангула. Корпускула допускает две основные формы. В одном случае она
получается путем последовательного склеивания односпиральных триангул по
граням. В результате такой склейки вторая триангулы будет сдвинута относительно
первой на 600.
В другом случае она формируется путем
антипаралельного склеивания разноспиральных триангул.
Корпускуляр - упорядоченная, замкнутая
последовательность(сумма) корпускул. Корпускуляр является мерой собственного
пространства корпускулярного типа. Это битриангуляр.
Он оже может иметь две формы. Одна форма образуется
путем последовательного соединения триангуляров, с одинаковой
спиральностью. Другая форма - путем антипаралельного склеивния разноспиральных
триангуляров.
Бикорпускуляр - склеивается из двух
битриангуляров, путем их последовательного, либо антипараллельного соединения.
При антипараллельном соединении мы получим совершенную
звезднотетраэдрическую монадную форму (или куб). При последовательном соединении
- четырехугольную пирамиду.
Данные монадные
формы определены с целью дать информации о возможных принципах формирования и
свойствах монадных кристаллов, в частности Платоновых
тел (рис.5).
рис. 6
В этом рисунке, характеризующем
элементарную ячейку гранецентрированной кубической решетки в явном
виде выделяются две диагональные триады (DEF, ABC), а
четвертая диагональ характеризует ось симметрии (ось вращения) такой ячейки (ось
KS).
1.3. ТРИАНГУЛЯРЫ И КОРПУСКУЛЯРЫ
Вводимые ниже определения являются робкой
попыткой автора осознать простую истину из вышеизложенного материала, что все
монадные формы формируются из треугольников и четырехугольников и потому
этот факт может быть как-то зафиксирован, пусть даже на уровне
информацию для размышления, отражающей важнейшие специфические свойства
всех монадных форм.
Двойственность монадных форм (треугольники и квадраты)
позволяет ввести для них специальные
категории.
Триангула -
это треугольная монадная
форма.
Триангуляр - упорядоченная, замкнутая последовательность (сумма) триангул.
Триангуляр есть мера собственного пространства монадных форм триангульного
типа. Элеентарный триангуляо-трехугольная
пирамида.
Корпускула - это четырехгранная монадная форма.
Это битриангула. Корпускула допускает две основные формы. В одном случае она
получается путем последовательного склеивания односпиральных триангул по
граням. В результате такой склейки вторая триангулы будет сдвинута относительно
первой на 600.
В другом случае она формируется путем
антипаралельного склеивания разноспиральных триангул.
Корпускуляр - упорядоченная, замкнутая
последовательность(сумма) корпускул. Корпускуляр является мерой собственного
пространства корпускулярного типа. Это битриангуляр.
Он оже может иметь две формы. Одна форма образуется
путем последовательного соединения триангуляров, с одинаковой
спиральностью. Другая форма - путем антипаралельного склеивния разноспиральных
триангуляров.
Бикорпускуляр - склеивается из двух
битриангуляров, путем их последовательного, либо антипараллельного соединения.
При антипараллельном соединении мы получим совершенную
звезднотетраэдрическую монадную форму (или куб). При последовательном соединении
- четырехугольную пирамиду.
Данные монадные
формы определены с целью дать информации о возможных принципах формирования и
свойствах монадных кристаллов, в частности Платоновых
тел (рис.5).
 рис. 7
Из рисунка
видно, что эволюция Платоновых тел вначале осуществляется от сферы к
формированию триангуляров, затем рождается совершенная форма, но уже
корпускулярная монадная форма (куб), а далее эволюция снова возвращается к
битриангулярным формам.
путем эволюция которых завершается
формированием другой совершенной монадной формы - сферы.
Поскольку в гексаде эволюции сфера
и куб находятся на одной и той же оси, то будем считать, что сфера является
совершенной формой корпускуляра. Поэтому можно считать, что все эволюционные
процессы монадных форм будут направлены от одной корпускулярной формы к
другой, через упорядоченную последовательность триангулярных и
битриангулярных форм.
В связи с этим имеет
смысл данные противоположные друг другу корпускулярные формы называть
соответственно женскими и мужскими корпускулярами. В этом проявляется
дуадность корпускуляров. Будем считать сферу женским корпускуляром, а куб
-мужским.
Будем условно считать,
что эта та изначальная двойственная пара (монада), которая порождает монадный
мир (порождающая как пространство, так и энергию).
1.4. СТРЕЛЫ ОПТИМАЛЬНОСТИ или
ВЕКТОРЫ
УСТРЕМЛЕНИЙ
Поскольку
любой эволюционный процесс характеризуется определенной направленностью, то
можно считать, что любая монадная форма, любой монадный кристалл может быть
"соткан" из векторов. Так, при анализе свойств Единого закона, будет обосновано,
что на первом этапе эволюция направлена к формированию корпускулярных форм
со специфическим вектором устремлений, направленного
вовне пространства монадной формы. Второй этап эволюции монадных форм, от
корпускулярных монадных форм к триангулярным, наоборот, характеризуется
вектором устремлений, направленного вовнутрь монадной формы.
На следующих рисунках приведены примеры 4-х типов
триангул и корпускул. Желтые и голубые триангулы имеют
разную спиральность.
рис. 7
Из рисунка
видно, что эволюция Платоновых тел вначале осуществляется от сферы к
формированию триангуляров, затем рождается совершенная форма, но уже
корпускулярная монадная форма (куб), а далее эволюция снова возвращается к
битриангулярным формам.
путем эволюция которых завершается
формированием другой совершенной монадной формы - сферы.
Поскольку в гексаде эволюции сфера
и куб находятся на одной и той же оси, то будем считать, что сфера является
совершенной формой корпускуляра. Поэтому можно считать, что все эволюционные
процессы монадных форм будут направлены от одной корпускулярной формы к
другой, через упорядоченную последовательность триангулярных и
битриангулярных форм.
В связи с этим имеет
смысл данные противоположные друг другу корпускулярные формы называть
соответственно женскими и мужскими корпускулярами. В этом проявляется
дуадность корпускуляров. Будем считать сферу женским корпускуляром, а куб
-мужским.
Будем условно считать,
что эта та изначальная двойственная пара (монада), которая порождает монадный
мир (порождающая как пространство, так и энергию).
1.4. СТРЕЛЫ ОПТИМАЛЬНОСТИ или
ВЕКТОРЫ
УСТРЕМЛЕНИЙ
Поскольку
любой эволюционный процесс характеризуется определенной направленностью, то
можно считать, что любая монадная форма, любой монадный кристалл может быть
"соткан" из векторов. Так, при анализе свойств Единого закона, будет обосновано,
что на первом этапе эволюция направлена к формированию корпускулярных форм
со специфическим вектором устремлений, направленного
вовне пространства монадной формы. Второй этап эволюции монадных форм, от
корпускулярных монадных форм к триангулярным, наоборот, характеризуется
вектором устремлений, направленного вовнутрь монадной формы.
На следующих рисунках приведены примеры 4-х типов
триангул и корпускул. Желтые и голубые триангулы имеют
разную спиральность.
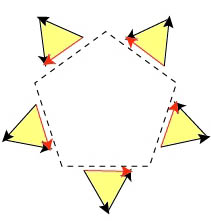
рис. 8 Цифры 1 и 2 также характеризуют эти формы, как имеющие разную спиральность и показывающие, как из триангул формируется корпускула (битриангула). Из рисунка видно два типа триангул. Одна триангула полностью замкнута, в то время как в другой замыкание осуществляется вектором, являющимся сумой двух других векторов. Эти вектора на рисунке обозначены красным цветом. Такие триангулы будем считать "заряженными". Конечно, это не единственный способ формирования корпускул из триангул. Рисунок характеризует только принципы формирования корпускул из триангул. Но эти принципы являются универсальными, всеобщими. Приведем теперь пример корпускуляров, сформированных из корпускул. Тогда, соединяя битриангулы III и IV через вершины, мы получим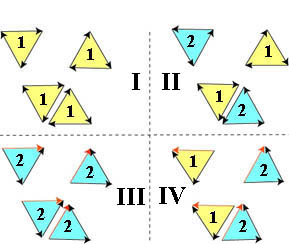
рис. 9 Этот рисунок показывает, как из корпускул формируется монадный цветок -корпускуляр. Это и есть совершенная монадная форма. Этот цветок состоит из трех "одноименных секций", сдвинутых друг относительно друга на 1200. В первом корпускуляре секции представляют собой последовательно соединенные "воронку и вихрь". Соединение этих секций в единый цветок порождает единую "стоячую волну". Система "воронка-вихрь", синхронно двигаясь по кругу, оказалась замкнутой. Во втором корпускуляре эти секции (корпускулы) представляют две "шестеренки", вращающиеся в противоположном направлении, а сам триангуляр оказлся трансформированным в новый корпускуляр, в котором противоположные триангулы сдвинуты друг относительно друг на 600. Эти системы интересны еще и тем, что удалив из оболочки одну, две. или даже 3 триангулы, мы все равно будем получать замкнутую "стоячую волну" ("воронка"-"вихрь"), например,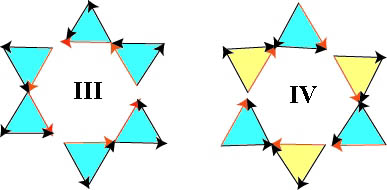
рис. 10 Однако эти цветки не формируют целостную систему, замкнутую оболочку. Триангулы отделены друг от друга корпускулами, а сформированная ими внутренняя силовая линия оказывается замкнутой. Поэтому они могут вращаться вокруг центрального "цветка". Ниже мы покажем, что такой тип оболочки присутствует в целостном монадном Цветке Жизни. Возможно, что в мире элементарных частиц эти монадные оболочки могут быть родоначальниками лептонного семейства. Существование векторов устремлений, имеющих противоположную направленность (и спиральность, позволяет ввести в рассмотрение положительные и отрицательные векторы (положительные либо отрицательные стрелы оптимальности). Например, можно говорить, что векторы устремлений, характеризующие эволюцию двойственной пары "сфера-куб" можно называть вектором, имеющим отрицательный заряд, в то время как вектор устремлений пары "куб-сфера" могут характеризоваться положительным зарядом. В каждой точке любой монадной формы можно определить свой собственный вектор устремлений, который будет однозначно характеризовать местоположение, собственное значение "веса" этой точки и ориентацию его в пространстве. Любая заряженная монадная форма имеет свою собственную стрелу оптимальности. Любая незаряженная монадная форма также имеет собственную стрелу оптимальности. В последнем случае стрела оптимальности будет характеризовать ось вращения (ось симметрии) уравновешенной монадой формы. Стрела оптимальности в разных научных приложениях может иметь разный смысл (мировая линия, спин, ось вращения, ось симметрии, и т.д.). Хочется отметить в этом направлении работы Бишкекской группы независимых ученых (подробнее), в работах которых на серьезном научном уровне обосновываются приоритеты асимметрии нашего мира и вводится понятие стрелы оптимальности. Но вот проблема взаимодействия стрел оптимальности, проблема того, как из асимметрии рождается симметрия, к сожалению, остается за "кадром" в оригинальных трудах этой группы ученых. Оказывается, что природа знает основы философии. Она знает закон отрицания отрицания, в соответствии с которым стрела оптимальности периодически меняет свое направление на противоположное, сменяя тезис на антитезис. Рассмотрим некоторые дополнительные свойства векторов устремлений.
 рис. 11
На данном рисунке вершины триангулятора <1,2,3,4> отражают последоватльнось
порождения триангулятора из триангул. Стрелки символизируют векторы
устремлений. Красные стрелки означают, что данный вектор устремлений не
является замкнутым для одной из граней триангулятора. Из рисунка видно, что
триангуляр является полностью уравновешенным монадным кристаллом. Так,
неуравновешенный в триангуле <1,2,4> вектор 4,2
оказывается уравновешен в триангуле <2,3,4>. То же самое можно сказать и про вектор устремлений 3,1. На других рисунках показаны примеры "склеек" уже триангуляров.
На рис. справа приведен пример недостроенного монадного кристалла.
Анализ Платоновых тел
показывает, что большинство этих монадных форм относятся к триангулярным.
Другими словами существование этих форм можно отождествить со свойствами
пространства, которое при отрицательном векторе устремлений является
расширяющимся, а при положительном векторе устремлений -
сжимающимся. Расширяющееся
пространство характеризуется увеличением "проявленной" массы, а сжимающееся - ее
уменьшением.
Триангулярный вектор устремлений обладает важным свойством. Зная
этот вектор мы однозначно можем с его вершины видеть все пространство, т.к. с
конца этого вектора оно будет видно как трехмерное. Другими словами конец
вектора устремления триангуляра будет всегда являться вершиной
тетраэдра. Отсюда вытекает важнейший вывод о трехмерности нашего
проявленного пространства, о трехмерности нашей Вселенной, о трехмерности
пространства монадных форм, о трехмерности Единого самосогласованного поля, о
трехмерности Единого Периодического закона.
Но какой же физический смысл
может быть заложен в корпускуляры?
Может быть корпускуляры связать
с энергией? Так, в силу
взаимодополнительности увеличение и уменьшение массы пространства напрямую
связаны с энергетикой. На первом этапе, как у маятника, происходит
увеличение трансформация потенциальной энергии в кинетическую, а на втором,
наоборот, кинетической в потенциальную.
Если триангулярный и
корпускулярный вектора устремлений будут перпендикулярны друг к другу, то
они могут взаимопревращаться друг в друга в процессе эволюции
монадной формы. Эти свойства могут порождать в монадных формах
различные типы полей, обладающих как потенциальной, так и кинетической
энергией.
Рассмотрим некоторые
специфичные свойства корпускуляров, на примере мужского корпускуляра. Монадная
форма такого корпускуляра является звездным тетраэдром (кубом). Она составлена
из двух триангулярных форм (тетраэдров), "склеенных" в единую форму. Но в
силу того, что векторы устремлений в каждом тетраэдре оказываются
противоположны, то такая склейка может выполняться таким образом, чтобы
суммарный вектор устремления звездного тетраэдра оказывался равным нулю.
Любое рассогласование векторов устремлений, выше определенного предела, в
"склеенных" тетраэдрах вызовет их расталкивание. Поскольку энергия
порождается женской формой корпускуляров, и снова поглощается этой же
формой.
В триангулах дело может
обстоять наоборот. После "склеивания" они стремятся к дальнейшему
присоединению и способствуют, тем самым, формированию массы, т.е. вектор
устремления массы стремится к центру масс.
Если сопоставить свойства данных типов монадных форм
(триангуляров и корпускуляров) и свойства типов элементарных частиц (бозоны и
фермионы), то невольно можно заметить между ними определенные аналогии. Трудно
сказать, случайность это, или совпадение, но свойства фермионов напоминают
свойства корпускуляров (в одном состоянии могут находиться только два фермиона с
противоположными спинами), а свойства бозонов напоминают
свойства триангул (в одном состоянии может находиться сколь угодно
много триангул). Из этих триангул можно "ткать нити", которые могут
сворачиваться в клубок.
Таковы
самые первые представления о пространстве и энергии монадных форм.
Только пространство и энергия (свет) являются той изначальной двойственной
парой, которая, собственно, является стоком и истоком эволюции любой
монадной формы. Заметим, что пространство и
энергия здесь никак не связаны со временем. Время
начинает проявляться тогда, когда появляется необходимость в синхронизации
подобных (триангулярных или корпускулярных) собственных пространств, когда
возникает необходимость инвариантных переходов из одного собственного
пространства монадных форм в другое.
2. КЛАССИФИКАЦИЯ
КРИСТАЛЛОВ
2.1.ТВЕРДЫЕ
КРИСТАЛЛЫ
Мир твердых кристаллов макромира чрезвычайно
многообразен и богат. Этот мир проявляется уже на уровне Периодической системы
химических элементов Д.И. Менделеева. Химикам известно, что каждый
химический элемент может иметь несколько форм, обладающих разными
химическими свойствами (изомеры- химические элементы, имеющие один и тот же
заряд ядра, но содержащих разное число нейтронов).
Оказывается, что изомеры могут иметь разные
структурные свойства, т.е. речь идет о химических элементах, имеющих совершенно один и тот же
состав, но обладающих разной внутренней структурой, как например, графит и
алмаз, обладают разной внутренней структурой. Подобные элементы академик Болотов
называет изостерами и приводит Периодическую таблицу химических элементов, как
некую периодизацию кристаллических элементов, в которой каждый химический
элемент имеет несколько изостеров.
1. Все изостеры одного и того же элемента
отличаются разной внутренней структурой, имеют разную "кристаллическую решетку".
2. Если в одном изостере нарушить хотя бы одну
связь в его "кристаллической решетке", то это может привести к измерению его
внутренней структуры и трансформацию в другой изостер.
3. Если в изостере изменить состав на 1
единицу, то изостер трансформируется в новый химический элемент с
соответствующей структурой "внутренней кристаллической решетки".
4. Все изостеры с одной
начальной структурой формируют единое периодическое подсемейство изостеров
химических элементов, т.е. Периодическая система химических элементов может
иметь несколько изостерных семейств Периодической системы химических элементов.
К такому выводу приводит закономерность о преемственности структуры изостерных
элементов. Спонтанные "мутации" приводят к изменению его внутренней структуры и
переход его в другое изостерное подсемейство.
Таким образом, изостеры
характеризуют многомерность даже в рамках одних и тех же химических элементов, с
одним и тем же количественным составом. Однако многие ученые не поняли смысл
открытия академика Б.В. Болотова, который вместо химического "элемента" ввел
понятие "изостер". Однако они и не отвергли это окрытие, возможно, потому,
что Б.В. Болотов к этому времени уже был академиком. А ведь это открытие можно
смело считать реформой Периодической системы химических элементов. Увы, этого не
произошло. Жаль, что это не известно широкому научному кругу.
Еще более жаль, что этот замечательный ученый и изобретатель уже ушел в мир
иной, так и не оцененный по достоинству за это поистине великое
открытие.
Но если химические
элементы обладают кристаллической решеткой, то они могут формировать, по образу
и подобию многомерные кристаллические решетки высших измерений, порождая мир
кристаллических форм.
рис. 11
На данном рисунке вершины триангулятора <1,2,3,4> отражают последоватльнось
порождения триангулятора из триангул. Стрелки символизируют векторы
устремлений. Красные стрелки означают, что данный вектор устремлений не
является замкнутым для одной из граней триангулятора. Из рисунка видно, что
триангуляр является полностью уравновешенным монадным кристаллом. Так,
неуравновешенный в триангуле <1,2,4> вектор 4,2
оказывается уравновешен в триангуле <2,3,4>. То же самое можно сказать и про вектор устремлений 3,1. На других рисунках показаны примеры "склеек" уже триангуляров.
На рис. справа приведен пример недостроенного монадного кристалла.
Анализ Платоновых тел
показывает, что большинство этих монадных форм относятся к триангулярным.
Другими словами существование этих форм можно отождествить со свойствами
пространства, которое при отрицательном векторе устремлений является
расширяющимся, а при положительном векторе устремлений -
сжимающимся. Расширяющееся
пространство характеризуется увеличением "проявленной" массы, а сжимающееся - ее
уменьшением.
Триангулярный вектор устремлений обладает важным свойством. Зная
этот вектор мы однозначно можем с его вершины видеть все пространство, т.к. с
конца этого вектора оно будет видно как трехмерное. Другими словами конец
вектора устремления триангуляра будет всегда являться вершиной
тетраэдра. Отсюда вытекает важнейший вывод о трехмерности нашего
проявленного пространства, о трехмерности нашей Вселенной, о трехмерности
пространства монадных форм, о трехмерности Единого самосогласованного поля, о
трехмерности Единого Периодического закона.
Но какой же физический смысл
может быть заложен в корпускуляры?
Может быть корпускуляры связать
с энергией? Так, в силу
взаимодополнительности увеличение и уменьшение массы пространства напрямую
связаны с энергетикой. На первом этапе, как у маятника, происходит
увеличение трансформация потенциальной энергии в кинетическую, а на втором,
наоборот, кинетической в потенциальную.
Если триангулярный и
корпускулярный вектора устремлений будут перпендикулярны друг к другу, то
они могут взаимопревращаться друг в друга в процессе эволюции
монадной формы. Эти свойства могут порождать в монадных формах
различные типы полей, обладающих как потенциальной, так и кинетической
энергией.
Рассмотрим некоторые
специфичные свойства корпускуляров, на примере мужского корпускуляра. Монадная
форма такого корпускуляра является звездным тетраэдром (кубом). Она составлена
из двух триангулярных форм (тетраэдров), "склеенных" в единую форму. Но в
силу того, что векторы устремлений в каждом тетраэдре оказываются
противоположны, то такая склейка может выполняться таким образом, чтобы
суммарный вектор устремления звездного тетраэдра оказывался равным нулю.
Любое рассогласование векторов устремлений, выше определенного предела, в
"склеенных" тетраэдрах вызовет их расталкивание. Поскольку энергия
порождается женской формой корпускуляров, и снова поглощается этой же
формой.
В триангулах дело может
обстоять наоборот. После "склеивания" они стремятся к дальнейшему
присоединению и способствуют, тем самым, формированию массы, т.е. вектор
устремления массы стремится к центру масс.
Если сопоставить свойства данных типов монадных форм
(триангуляров и корпускуляров) и свойства типов элементарных частиц (бозоны и
фермионы), то невольно можно заметить между ними определенные аналогии. Трудно
сказать, случайность это, или совпадение, но свойства фермионов напоминают
свойства корпускуляров (в одном состоянии могут находиться только два фермиона с
противоположными спинами), а свойства бозонов напоминают
свойства триангул (в одном состоянии может находиться сколь угодно
много триангул). Из этих триангул можно "ткать нити", которые могут
сворачиваться в клубок.
Таковы
самые первые представления о пространстве и энергии монадных форм.
Только пространство и энергия (свет) являются той изначальной двойственной
парой, которая, собственно, является стоком и истоком эволюции любой
монадной формы. Заметим, что пространство и
энергия здесь никак не связаны со временем. Время
начинает проявляться тогда, когда появляется необходимость в синхронизации
подобных (триангулярных или корпускулярных) собственных пространств, когда
возникает необходимость инвариантных переходов из одного собственного
пространства монадных форм в другое.
2. КЛАССИФИКАЦИЯ
КРИСТАЛЛОВ
2.1.ТВЕРДЫЕ
КРИСТАЛЛЫ
Мир твердых кристаллов макромира чрезвычайно
многообразен и богат. Этот мир проявляется уже на уровне Периодической системы
химических элементов Д.И. Менделеева. Химикам известно, что каждый
химический элемент может иметь несколько форм, обладающих разными
химическими свойствами (изомеры- химические элементы, имеющие один и тот же
заряд ядра, но содержащих разное число нейтронов).
Оказывается, что изомеры могут иметь разные
структурные свойства, т.е. речь идет о химических элементах, имеющих совершенно один и тот же
состав, но обладающих разной внутренней структурой, как например, графит и
алмаз, обладают разной внутренней структурой. Подобные элементы академик Болотов
называет изостерами и приводит Периодическую таблицу химических элементов, как
некую периодизацию кристаллических элементов, в которой каждый химический
элемент имеет несколько изостеров.
1. Все изостеры одного и того же элемента
отличаются разной внутренней структурой, имеют разную "кристаллическую решетку".
2. Если в одном изостере нарушить хотя бы одну
связь в его "кристаллической решетке", то это может привести к измерению его
внутренней структуры и трансформацию в другой изостер.
3. Если в изостере изменить состав на 1
единицу, то изостер трансформируется в новый химический элемент с
соответствующей структурой "внутренней кристаллической решетки".
4. Все изостеры с одной
начальной структурой формируют единое периодическое подсемейство изостеров
химических элементов, т.е. Периодическая система химических элементов может
иметь несколько изостерных семейств Периодической системы химических элементов.
К такому выводу приводит закономерность о преемственности структуры изостерных
элементов. Спонтанные "мутации" приводят к изменению его внутренней структуры и
переход его в другое изостерное подсемейство.
Таким образом, изостеры
характеризуют многомерность даже в рамках одних и тех же химических элементов, с
одним и тем же количественным составом. Однако многие ученые не поняли смысл
открытия академика Б.В. Болотова, который вместо химического "элемента" ввел
понятие "изостер". Однако они и не отвергли это окрытие, возможно, потому,
что Б.В. Болотов к этому времени уже был академиком. А ведь это открытие можно
смело считать реформой Периодической системы химических элементов. Увы, этого не
произошло. Жаль, что это не известно широкому научному кругу.
Еще более жаль, что этот замечательный ученый и изобретатель уже ушел в мир
иной, так и не оцененный по достоинству за это поистине великое
открытие.
Но если химические
элементы обладают кристаллической решеткой, то они могут формировать, по образу
и подобию многомерные кристаллические решетки высших измерений, порождая мир
кристаллических форм.

 рис. 12
И весь этот сказочно богатый
мир кристаллов сложен в конечном итоге из треугольников и
четырехугольников.
Но в конечном итоге
весь этот бесконечно многообразный мир кристаллов состоит всего лишь из двух
взаимодополнительных групп, отражающих янский, или
иньский аспект
рис. 12
И весь этот сказочно богатый
мир кристаллов сложен в конечном итоге из треугольников и
четырехугольников.
Но в конечном итоге
весь этот бесконечно многообразный мир кристаллов состоит всего лишь из двух
взаимодополнительных групп, отражающих янский, или
иньский аспект
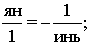 Иньские кристаллы не имеют
"шипов". Их грани формируются пирамидами, все вершины которых совмещены в центре
кристалла. Янские кристаллы формируются уже удвоенными пирамидами, одна вершина
которой находится в центре кристалла, а другая формирует "шип"
кристалла.
В этой связи особый интерес для нас
представляет звездный тетраэдр
Иньские кристаллы не имеют
"шипов". Их грани формируются пирамидами, все вершины которых совмещены в центре
кристалла. Янские кристаллы формируются уже удвоенными пирамидами, одна вершина
которой находится в центре кристалла, а другая формирует "шип"
кристалла.
В этой связи особый интерес для нас
представляет звездный тетраэдр
 Это янский кристалл, которому соответствует женский
кристалл -октаэдр.
Выражая отношения между октаэдром и звездным
тетраэдром через отношения "число вершин /число граней", получим следующее
тождество,
Это янский кристалл, которому соответствует женский
кристалл -октаэдр.
Выражая отношения между октаэдром и звездным
тетраэдром через отношения "число вершин /число граней", получим следующее
тождество,
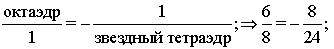 ,
отражающего отношения между мужским и женским началом
в этих кристаллах.
Но выше мы уже говорили о том, что куб и октаэдр
взаимодополнительны и эта взаимодополнительность может быть отражена
тождеством
,
отражающего отношения между мужским и женским началом
в этих кристаллах.
Но выше мы уже говорили о том, что куб и октаэдр
взаимодополнительны и эта взаимодополнительность может быть отражена
тождеством
 Таким образом, использование вышеприведенных
тождеств позволяет проводить классификацию кристаллов с позиций природных
операционных механизмов Единого закона эволюции двойственных
отношений.
2.2. ЖИДКИЕ
КРИСТАЛЛЫ
Жидкий кристалл - это особое состояние вещества, промежуточное между жидким
и твердым состояниями. В жидкости молекулы могут свободно
вращаться и перемещаться в любых направлениях. В кристаллическом твердом теле
они расположены по узлам правильной геометрической сетки, называемой
кристаллической решеткой, и могут лишь вращаться в своих фиксированных позициях.
В жидком кристалле имеется некоторая степень геометрической упорядоченности в
расположении молекул, но допускается и некоторая свобода перемещения.
Считается, что состояние жидкого кристалла открыл в 1888 австрийский ботаник
Ф.Рейнитцер. Он изучал поведение органического твердого вещества, называемого
холестерилбензоатом. При нагревании это соединение переходило из твердого в
мутное на вид состояние, ныне называемое жидкокристаллическим, а затем в
прозрачную жидкость; при охлаждении последовательность превращений повторялась в
обратном порядке. Рейнитцер отметил также, что при нагревании изменяется цвет
жидкого кристалла – от красного к синему, с повторением в обратном порядке при
охлаждении. Почти все жидкие кристаллы, обнаруженные на сегодняшний день,
представляют собой органические соединения; примерно 50% всех известных
органических соединений при нагревании образуют жидкие кристаллы. В литературе
описаны также жидкие кристаллы некоторых гидроксидов (например, Fe2O3ЧxH2O).
Консистенция жидких кристаллов может быть разной – от легкотекучей жидкой до
пастообразной. Жидкие кристаллы имеют необычные оптические свойства, что
используется в технике.
Известно,
что при нагревании некоторых твердых органических соединений их кристаллическая
решетка разваливается и образуется жидкий кристалл. Если температуру повышать и
далее, то жидкий кристалл переходит в настоящую жидкость. Жидкие кристаллы,
образующиеся при нагревании, называются термотропными. В конце 1960-х годов были получены
органические соединения, являющиеся жидкокристаллическими при комнатной
температуре.
Но существует и
другой способ получения жидких кристаллов – обработка некоторых соединений
контролируемым количеством воды или другого полярного растворителя. (Полярным
называется растворитель, состоящий из молекул-диполей, на одном конце которых
находится положительный электрический заряд, а на другом – отрицательный.)
Жидкие кристаллы, состоящие из двух и более компонентов, называются лиотропными. Их можно получать, смешивая с водой
такие материалы, как мыла, детергенты, полипептиды, жирные кислоты, соли жирных
кислот и фосфолипиды.
Жидкие кристаллы образуются из молекул, имеющих разную геометрическую форму
(чаще всего – удлиненных или дискообразных). Электрическими межмолекулярными
силами определяется характер «упаковки» молекул, т.е. то, как они геометрически
соотносятся друг с другом.
Расположение молекул в жидких
кристаллах изменяется под действием таких факторов, как температура, давление,
электрические и магнитные поля; изменения же расположения молекул приводят к
изменению оптических свойств, таких, как цвет, прозрачность и способность к
вращению плоскости поляризации проходящего света. На всем этом основаны
многочисленные применения жидких кристаллов.
Так, жидкие кристаллы широко применяются
в производстве наручных часов и небольших калькуляторов. Создаются плоские
телевизоры с тонким жидкокристаллическим экраном, и т.д..
И хотя для жидких кристаллов отсутствуют такая же подробная классификация, как
для твердых кристаллов, однако, в соответствии с природными операционными
механизмами Единого закона можно смело выдвинуть гипотезу о том, что мир жидких
кристаллов столь же богат и разнообразен, как и мир тверддых
кристаллов.
Таким образом, использование вышеприведенных
тождеств позволяет проводить классификацию кристаллов с позиций природных
операционных механизмов Единого закона эволюции двойственных
отношений.
2.2. ЖИДКИЕ
КРИСТАЛЛЫ
Жидкий кристалл - это особое состояние вещества, промежуточное между жидким
и твердым состояниями. В жидкости молекулы могут свободно
вращаться и перемещаться в любых направлениях. В кристаллическом твердом теле
они расположены по узлам правильной геометрической сетки, называемой
кристаллической решеткой, и могут лишь вращаться в своих фиксированных позициях.
В жидком кристалле имеется некоторая степень геометрической упорядоченности в
расположении молекул, но допускается и некоторая свобода перемещения.
Считается, что состояние жидкого кристалла открыл в 1888 австрийский ботаник
Ф.Рейнитцер. Он изучал поведение органического твердого вещества, называемого
холестерилбензоатом. При нагревании это соединение переходило из твердого в
мутное на вид состояние, ныне называемое жидкокристаллическим, а затем в
прозрачную жидкость; при охлаждении последовательность превращений повторялась в
обратном порядке. Рейнитцер отметил также, что при нагревании изменяется цвет
жидкого кристалла – от красного к синему, с повторением в обратном порядке при
охлаждении. Почти все жидкие кристаллы, обнаруженные на сегодняшний день,
представляют собой органические соединения; примерно 50% всех известных
органических соединений при нагревании образуют жидкие кристаллы. В литературе
описаны также жидкие кристаллы некоторых гидроксидов (например, Fe2O3ЧxH2O).
Консистенция жидких кристаллов может быть разной – от легкотекучей жидкой до
пастообразной. Жидкие кристаллы имеют необычные оптические свойства, что
используется в технике.
Известно,
что при нагревании некоторых твердых органических соединений их кристаллическая
решетка разваливается и образуется жидкий кристалл. Если температуру повышать и
далее, то жидкий кристалл переходит в настоящую жидкость. Жидкие кристаллы,
образующиеся при нагревании, называются термотропными. В конце 1960-х годов были получены
органические соединения, являющиеся жидкокристаллическими при комнатной
температуре.
Но существует и
другой способ получения жидких кристаллов – обработка некоторых соединений
контролируемым количеством воды или другого полярного растворителя. (Полярным
называется растворитель, состоящий из молекул-диполей, на одном конце которых
находится положительный электрический заряд, а на другом – отрицательный.)
Жидкие кристаллы, состоящие из двух и более компонентов, называются лиотропными. Их можно получать, смешивая с водой
такие материалы, как мыла, детергенты, полипептиды, жирные кислоты, соли жирных
кислот и фосфолипиды.
Жидкие кристаллы образуются из молекул, имеющих разную геометрическую форму
(чаще всего – удлиненных или дискообразных). Электрическими межмолекулярными
силами определяется характер «упаковки» молекул, т.е. то, как они геометрически
соотносятся друг с другом.
Расположение молекул в жидких
кристаллах изменяется под действием таких факторов, как температура, давление,
электрические и магнитные поля; изменения же расположения молекул приводят к
изменению оптических свойств, таких, как цвет, прозрачность и способность к
вращению плоскости поляризации проходящего света. На всем этом основаны
многочисленные применения жидких кристаллов.
Так, жидкие кристаллы широко применяются
в производстве наручных часов и небольших калькуляторов. Создаются плоские
телевизоры с тонким жидкокристаллическим экраном, и т.д..
И хотя для жидких кристаллов отсутствуют такая же подробная классификация, как
для твердых кристаллов, однако, в соответствии с природными операционными
механизмами Единого закона можно смело выдвинуть гипотезу о том, что мир жидких
кристаллов столь же богат и разнообразен, как и мир тверддых
кристаллов.
Предупреждение:
Далее идут, мягко говорря, не проверненные и неподтвержденные сведения, даже откровенная мистика...
Так, про теории Гаряева: Волновая мистика П.Гаряева.2.3. ПЛАЗМЕННЫЕ КРИСТАЛЛЫ В своей книге "Теория кристаллизации плазмы" Владимир Тимофеевич Гринев( diplazmv56@mail.ru) пишет о том, что вот уже 20 лет существует настоящее фундаментальное открытие, способное инициировать фейерверк фантастических изобретений, и способное в полной мере удовлетворить самые смелые ожидания. Его основная суть в том, что удалось разгадать свойства вещества при температурах в сотни миллионов градусов. "По существу, открыто принципиально новое, пятое состояние вещества. Ему дано условное название "ПЛАЗМЕННЫЙ КРИСТАЛЛ" (ПК) или "КРИСТАЛЛИЧЕСКАЯ ПЛАЗМА". Как оказалось, при очень высокой температуре вещество, уже, не может находиться в состоянии плазмы, и самопроизвольно, скачкообразно, переходит в принципиально иное состояние. Поняты основные причины и законы этого перехода. Выяснены основные свойства вещества в этом состоянии. Обнаружено множество уже существующих и широко известных экспериментальных фактов прямо подтверждающих существование вышеназванного состояния вещества. Более того - найдены решения, позволяющие получать ПК в лаборатории. Как выяснилось, ПК обладают многими фантастическими свойствами. Например, их совершенно не нужно удерживать, как пытаются удержать плазму. При остывании ПК лавинообразно переходит в состояние обычной плазмы и взрывается, как взрывается шаровая молния. В принципе, шаровая молния это и есть кусочек вещества в пятом состоянии. ПК (шаровые молнии) могут использоваться как реакторы управляемого ядерного синтеза, как установки управляемой мутации химических элементов - из водорода можно получать в промышленных масштабах любой химический элемент, от гелия до урана и золота. При этом, термоядерные реакторы на ПК это относительно простые, надежные, недорогие устройства, совершенно непохожие на современные установки, работающие по совершенно по другому принципу, абсолютно безопасные в эксплуатации, не нарабатывающие радиоактивные отходы, обеспечивающие прямое преобразование энергии ядерного синтеза в электрическую и способные использовать в качестве топлива не только дейтерий и тритий, но и множество других химических элементов. ПК могут быть использованы как генераторы сверхмощного когерентного излучения в любом диапазоне, от радиоволн до жесткого ядерного излучения (рентгеновский лазер например), и как сверхчувствительные радиоприемники того же диапазона". В моих монографиях [1] и [2] приводятся другие дополнительные обоснования свойств плазменных кристаллов. В соответствии с едиными природными операционными принципами Единого закона эволюции двойственных отношений были приведены свойства "горячих", поистине звездной Периодической системе элементов - астроноидов еще в 1999 году. Кроме того, информация о свойствах этих поистине звездных кристаллов приводится и на страницах данного сайта (О космологии). Но кто из ученых заинтересовался данными публикациями? Никто! Разве может "серьмяжный мужик" написать что-то такое, что их благородиям не известно? А потому их вывод однозначен -лжеистина. 2.4. ВОЛНОВЫЕ КРИСТАЛЛЫ Современная наука уже имеет достаточно хорошие представления и о свойствах кристаллов совершенно иного уровня - волновых кристаллов. Эти кристаллы также, по образу и подобию порождаются природными операционными механизмами Единого закона. Об этом свидетельствуют публикации П.Гаряева (Волновой генетический код), И.И. Дороднова (Дороднов И.И. ) и других авторов. Уже существуют практические доказательства существования волнового уравнения Единого закона (Волновой геном), формирующего двойные спирали волновых функций. Известно, что волны любой природы характеризуются длиной волны (l) и ее периодом (t),а их взаимодействие описывается в рамках передатчика (прд) и приемника (прм) волнового излучения, которые могут двигаться друг относительно друга.
 рис. 13
Подобное взаимодействие порождает весы монады
рис. 13
Подобное взаимодействие порождает весы монады
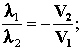 При движении приемника и
передатчика с одной и той же скоростью, в одном и том же направлении,
длина волны остается неизменной (равновесное
состояние).
При увеличении скорости движения передатчика в
направлении движения волны, длина волны уменьшается. При увеличении скорости
приемника волны (навстречу фронту волны) соответственно уменьшается длина
принимаемой волны. И это наглядно видно из
тождества.
Более наглядно смысл этого тождества можно получить
из следующего рисунка
При движении приемника и
передатчика с одной и той же скоростью, в одном и том же направлении,
длина волны остается неизменной (равновесное
состояние).
При увеличении скорости движения передатчика в
направлении движения волны, длина волны уменьшается. При увеличении скорости
приемника волны (навстречу фронту волны) соответственно уменьшается длина
принимаемой волны. И это наглядно видно из
тождества.
Более наглядно смысл этого тождества можно получить
из следующего рисунка
 рис. 14
Видите, как естественно волновые весы монады
порождают равновесные состояния, в которых нет волны?
Многомерный характер весов монады порождает
многомерную волновую "кристаллическую решетку".
рис. 14
Видите, как естественно волновые весы монады
порождают равновесные состояния, в которых нет волны?
Многомерный характер весов монады порождает
многомерную волновую "кристаллическую решетку".
 рис. 15
И мы
возвращаемся в лоно природных операционных механизмов Единого закона
эволюции двойственного отношения. Из этого кубика более наглядно
модно представить себе, что "дефекты" двойственного отношения вида
рис. 15
И мы
возвращаемся в лоно природных операционных механизмов Единого закона
эволюции двойственного отношения. Из этого кубика более наглядно
модно представить себе, что "дефекты" двойственного отношения вида
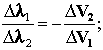 не могут не порождать сжатия (растяжения) структуры
волнового кубика, и могут вызывать преобразование физических размеров всего
"кубика", а не только и исключительно, длины, ширины, высоты, времени, длины
волны, периода и других волновых характеристик.
Кристаллическая решетка формируется природными операционными механизмами Единого
закона эволюции двойственного отношения и потому она проявляется во всех земных
и небесных сферах.
Корпускулярно-волновое единство структуры и функции,
частицы и волны наиболее ярко проявляются в Периодической системе химических
элементов.
не могут не порождать сжатия (растяжения) структуры
волнового кубика, и могут вызывать преобразование физических размеров всего
"кубика", а не только и исключительно, длины, ширины, высоты, времени, длины
волны, периода и других волновых характеристик.
Кристаллическая решетка формируется природными операционными механизмами Единого
закона эволюции двойственного отношения и потому она проявляется во всех земных
и небесных сферах.
Корпускулярно-волновое единство структуры и функции,
частицы и волны наиболее ярко проявляются в Периодической системе химических
элементов.
 рис. 16
Данный рисунок представляет
собой двойную спираль "волновых кубиков" Периодической системы химических элементов. Эта структура
отражает собой совокупность полностью заполненных кристаллических оболочек (и
подоболочек) Периодической системы химических
элементов.
И хотя эта структура
является гипотетичной и ее еще долго не будут замечать в упор, но эта гипотеза
основывается на природных операционных принципах Единого
закона.
Посмотрите, как естественно в IV периоде из волновых кубиков
формируется ГиперКуб.
Как здесь снова не вспомнить библию "И последний
становится Первым". Может быть, кому то мои восклицания по данному поводу уже
"набили оскомину", но я прошу меня простить за эти и иные повторы,
которые я постоянно использую на разных страницах, но ... "повторение-мать
учения".
Посмотрите, IV период полностью соответствует свойствам матрицы И-Цзин (Книга
перемен).
рис. 16
Данный рисунок представляет
собой двойную спираль "волновых кубиков" Периодической системы химических элементов. Эта структура
отражает собой совокупность полностью заполненных кристаллических оболочек (и
подоболочек) Периодической системы химических
элементов.
И хотя эта структура
является гипотетичной и ее еще долго не будут замечать в упор, но эта гипотеза
основывается на природных операционных принципах Единого
закона.
Посмотрите, как естественно в IV периоде из волновых кубиков
формируется ГиперКуб.
Как здесь снова не вспомнить библию "И последний
становится Первым". Может быть, кому то мои восклицания по данному поводу уже
"набили оскомину", но я прошу меня простить за эти и иные повторы,
которые я постоянно использую на разных страницах, но ... "повторение-мать
учения".
Посмотрите, IV период полностью соответствует свойствам матрицы И-Цзин (Книга
перемен).