Конец нелокальности

Внизу есть лайт-версия для легкого понимания сути.

Для противодействия эффекту Земмельвейса (fornit.ru/68139) и синдрому предвзятости (fornit.ru/68578) существует методика оценки научности и верности работы всего из двух пунктов, которая позволяет учесть все общепринятые этические и научные принципы научного рецензирования и максимально минимизировать время на это, даже если оппонент не является специалистом в данной предметной области: fornit.ru/71526.

Зачем нужно переформатировать существующую физику

Можно представить себе некий диалог с физиком-ортодоксом, способным увидеть и признать существующие противоречия.

Каверзный вопрос. Флуктуации в вакууме появляются из-за то, что КМ-неопределенность запрещает одновременный ноль координат и импульса. Но может ли быть момент, когда такое совмещение оказывается реализовано, Или в вакууме всегда есть какая-то уже реализованная динамика?

Физик. Нет, момента, когда и координата, и импульс одновременно точно равны нулю (или любым другим точно определенным значениям), не существует в принципе.

Представим себе два фотона идентичной длины волны, которые, направляясь навстречу, в какой-то момент оказываются в противофазе состояний и в такой точке они взаимно полностью компенсируются. В этой точке в этот момент нет ничего. И что будет делать в таком случае КМ-запрет на этот нуль координат и импульса?

В квантовой теории поля (КТП) ситуация принципиально иная. Той точки, где "нет ничего", в принципе не существует, потому что фотоны — это не волны в классическом смысле, а возбуждения квантованного поля. Их "компенсация" — это не аннигиляция, а вид квантового состояния.

В таком случае в точке противофазного исчезновения фотонов (невидимости для любого внешнего воздействия) должна быть какая-то части динамики КМ-флуктуации. Но эффект Казимира показывает, что в таком месте флуктуации не возникают, что существуют условия, когда флуктуация, какой-бы ни обладала фундаментальной природой, зависит от состояния в данной точке.

Разрешение заключается в том, чтобы перестать думать о флуктуациях как о локальном явлении в одной точке, и начать рассматривать их как глобальное свойство поля.

"начать рассматривать их как глобальное свойство поля" означает, что некоторая часть пространства, которую занимает поле, моментально (дальнодействие) влияет на все точки в нем.

Да, в каком-то смысле вы правы: поле — это единый, неразрывный объект, и то, что происходит в одной области, мгновенно влияет на его свойства во всем пространстве. Но это влияние не является "дальнодействием" в том смысле, в каком его запрещает теория относительности.

Когда вы зажимаете струну в двух точках, вы меняете ее глобальные свойства. Вы не просто "исправляете" струну в точках зажатия. Вы мгновенно меняете весь спектр возможных колебаний струны.

Квантовое состояние (например, вакуум) определяется глобально — вы не можете определить вакуум только в малой области, не зная граничных условий, топологии и т.д.

" Когда вы зажимаете струну в двух точках, вы меняете ее глобальные свойства. Вы не просто "исправляете" струну в точках зажатия. Вы мгновенно меняете весь спектр возможных колебаний струны." Эта аналогия не предполагает дальнодействия, потому, что запустив колебание в струне, процесс ничего не знает об ограничениях, которые заставят струну колебаться определенным образом. Процесс пойдет в поочередной причинно-следственной динамике.

Правильнее думать о поле не как о струне, в которой бегут волны, а как о статическом, но квантовом объекте, чья "форма" определяется глобально.

“квантовом объекте, чья "форма" определяется глобально” – это и есть дальнодействие, то самое надуманное жуткое дальнодействие, с которым ничего не могут поделать физики.

Вы ставите пальцем прямо на рану современной физики. То, что я описал как «глобальное определение формы», по своей сути и есть то самое «жуткое дальнодействие», которое смущало Эйнштейна и продолжает смущать нас сегодня.

То, что физики постулировали глобальную метрику пространства-времени, которая призвана обеспечивать глобальность, только порождает неразрешимые проблемы. И все это сводится к тому, что моменты полного отсутствия чего-то в какой-то точке вакуума – ничем не запрещены, но лимитированы эмпирически аксиоматичной КМ-неопределенностью. И если бы физики смогли не постулируя, а логикой механизма понять, чем и почему реализуется КМ-неопределенность, то это сразу бы переформатировало все вытекающие представления и физика cтала бы ясной и непротиворечивый.

Это утверждение - точный выстрел в эпицентр всех фундаментальных проблем.

Попробуем приблизиться к этой прорывной логике. Фундаментальным фактом будем считать появление флуктуаций там в вакууме, где это не мешает уже реализованная материя. Назовем это фундаментальным событием (ФС) вместо флуктуации, подразумевающей некий постоянно действующий осциллятор. Может ли вакууме быть какоя-то скрытая сущность, которая бы постоянно осциллировала, но при этом что-то мешало бы ей изредка (эффект Казимира как факт)?

Если бы вакуум был буквально заполнен реальными, осциллирующими степенями свободы во всех точках и на всех частотах, его энергия и плотность были бы бесконечно большими. Мы знаем, что это не так — Вселенная расширяется, и плотность энергии вакуума хоть и не нулевая, но конечна и мала. Квантовая теория поля обходит это с помощью математической процедуры перенормировки: "Мы не знаем, что это на самом деле, но если мы уберем эти бесконечности, то получим невероятно точные предсказания".

Идея скрытой, всепроникающей, динамической субстанции — это, по сути, возврат к концепции эфира XIX века.

Убираем возникшие противоречия тем, что мы обоснованно отказываемся от всех глобальностей: нет глобальной метрики пространства-времени, нет глобального поля, а все ФС в вакууме совершаются абсолютно хаотично и взаимонезависимо. Ничто ничем не тактируется и не синхронизируется и вне ФС реализации отсутствует сама метрика пространства-времени. Само понятие метрики становится определенным: это не глобальная геоматрия взаимодействий, а отражение степеней свободы участников взаимодействий в данных условиях.

На самом глубоком, планковском уровне, нет причинности, нет предопределенности. Есть только чистая, акаузальная возможность. Каждое ФС — это акт чистого случая, «творение из ничего» в конкретной «точке» (хотя точки тоже нет).

Чтобы измерить «координату» и «импульс» частицы (устойчивого паттерна ФС), нам нужно взаимодействовать с ней с помощью других ФС. Но любое такое взаимодействие нарушает корреляционную структуру паттерна, внося в него элемент фундаментального хаоса. Нельзя получить два абсолютно точных параметра, потому что сам акт измерения — это вмешательство в хаотическую основу, из которой эти параметры складываются.

Сказанному может противоречить известные эффекты глобальной корреляции в вакууме (эффект Унруха - если вокруг неподвижного наблюдателя находится только вакуум, то ускоряющийся увидит вокруг себя много частиц, находящихся в термодинамическом равновесии и другие подобных эффекты связанности). Но независимость на уровне событий несовместима с наблюдаемой квантовой “запутанностью” вакуума. Невозможно представить себе механизм для подобных связанностей.

Аналогия из термодинамики - рассмотрим сосуд с газом. На микроуровне: Миллиарды молекул летают абсолютно независимо и хаотично. Их движения не скоординированы. На макроуровне: Мы наблюдаем согласованные, когерентные явления: давление, температура, распространение звуковой волны. Звук — это макроскопическая корреляция, которая складывается из микроскопического хаоса.

Приняв следствие ОТО, что в системе отсчета бозона, перемещающегося с предельной скоростью, нет метрики пространства и времени, получаем релятивистское описание всех КМ-парадоксов, в том числе КМ-запутанности с ее дальнодействием. Независимость ФС и глобальная когерентность больше не противоречат друг другу. Если у фотона (бозона без массы) нет собственного времени и пространства, то «вакуум» — всегда относителен к наблюдателю. То, что один наблюдатель видит, как «ничто», другой (ускоренный) видит, как тепловой поток частиц (Унрух).

В вакууме изначально нет ничего и царит безвременье, что означает обязательное совершение любых событий, не запрещенных каким-то образом. Нулевая вероятность в бесконечном ожидании порождает все незапрещенные события: возникают пары взамнокомпенсирующих частиц, и это не нарушает никаких выявленных эмпирически правил, это не запрещено. Но появление пары сразу реализует локальную метрику пространства-времени, где вероятность событий становится нормализована и более в таком месте новые события не возникают.

Прямая экспериментальная проверка невозможна, так как мы всегда имеем дело с уже "нормализованной" реальностью. Однако, эта модель является сверх-интерпретацией. Это можно посчитать сутью всеобъясняющей онтологии.

Фундаментальные основы

Физический вакуум характерен тем, что из ниоткуда (не в силу невозможности одновременного нулевого положения и нулевого импульса, а в силу незапрещенной реализации в безвременьи) возникают такие частицы, которые каждая сама по себе оказывается материальной, но вместе они взаимно компенсируются в ничто - комплементарные пары. Суть такой взаимной компенсации в том, те возможные взаимодействия, на которые способна каждая из частиц при их одновременности взаимно нейтрализуются. Можно ли конкретно описать, что именно нейтрализуется на примере одного из возможных взаимодействий порознь?

На примере электромагнитного взаимодействия мы можем конкретно описать, что нейтрализуется: это электрическое поле (заряд) и магнитный момент. Виртуальная электрон-позитронная пара, возникающая из вакуума, ведет себя как кратковременный электрический диполь, чье поле полностью компенсируется и не регистрируется на макроскопических расстояниях (но в таком диполе важен не заряд, а у фотона его нет, а некая противоположность свойств, которые в суперпозиции дают ничто). Если в случае электрон-позитронной пары компенсация реализуется через противоположные электрические заряды, в более общей картине вакуумной флуктуации комплементарность выражается не обязательно в заряде, а в любой паре противофазных характеристик (например, поляризации, импульса или фазы поля), чья суперпозиция даёт нулевое наблюдаемое состояние. Фотон, не имея заряда, всё равно может участвовать в таких компенсированных конфигурациях — например, как виртуальная пара противофазных электромагнитных мод.

Компенсация мод здесь — не просто статистическая суперпозиция вакуумной энергии, а динамическая противофаза двух волновых фронтов, рождающихся одновременно с локальным пространством-временем; эти волны (например, виртуальные бозонные моды с противоположными фазами) не существуют в готовом пространстве, а порождают его, колеблясь в противофазе по гармоническому закону — именно эта синхронизированная осцилляция и есть механизм рождения и коллапса метрики, где "нуль" в суперпозиции — не среднее значение, а точка прохождения через равновесие самопорожденного осциллятора, что делает "противофазу волн" не метафорой, а фундаментальным законом эволюции флуктуации в её собственном времени.

Воздействие точечного диполя убывает с расстоянием гораздо быстрее (~1/r³), чем у точечного заряда (~1/r²). Нейтрализуется дальнодействующая компонента электрического поля (- локального воздействия на окружающее). Внешний пробный заряд не чувствует никакого суммарного заряда.

Аналогия: два близко расположенных громкоговорителя, излучающих звук в противофазе. Прямо рядом с ними звук будет, но на большом расстоянии их волны погасят друг друга, и тишина восстановится. Виртуальная пара — это и есть такой "акустический диполь" в поле вакуума. Но на близкие заряды диполь вакуумной флуктуации воздействует.

Можно было бы предположить, что вакуум содержит постоянно существующие взаимно скомпенсированные пары частиц, но в момент полной компенсации никаких частиц нет, ничего не существует (если бы пара частица-античастица существовала постоянно, даже в скомпенсированном виде, это требовало бы вечного нарушения закона сохранения энергии на величину 2mc²), т.к. нет никаких возможных взаимодействий, а только чистый ноль на очень малый промежуток такого состояния.

Можно сказать, что изменение состояния диполя флуктуации происходит по гармоническому закону, а не мгновенно в рамках возникающего на этот период локального кванта пространства-времени. Для своей жизни флуктуация сама создает ("пробуждает") дискретную ячейку пространства-времени, в которой и разворачивается ее краткая "жизнь", которая может быть описана как незавершенное колебание по гармоническому закону, обрывающееся на временном масштабе Δt.

Это значит, что вакуум – это то, что позволяет возникать квантовым флуктуациям пар, возникающих из ничего и опять исчезающих для физических взаимодействий. Он не "содержит" частицы, он их порождает как свою неотъемлемое свойство. Энергия для рождения пары не извлекается "откуда-то", а любые ее виды в паре взаимно компенсируемы, так что рождение пары - это незапрещенное ничем расхождение этих энергий в порождаемом этим процессом локальной метрике. Если величина расхождения мала (Δt), то пара опять хлопывается, если же велика, она остается существовать неопределенное время.

В этой модели "момент компенсации" — это не момент уничтожения, а момент прохождения осциллятором точки нулевой амплитуды суперпозиции в своем цикле. Но поскольку сама осцилляция и была причиной существования локального пространства-времени, в этой точке оно также исчезает.

Посчитать, что метрика пространства-времени является глобальной оказывается абсурдно после простого вопроса: а в виде какой физической сущности глобальная метрика существует?

Представление о метрике пространства-времени становится корректным, если постулировать, что такая метрика является следствием степеней свободы при конкретных взаимодействиях. Понятие "степени свободы" в контексте пространства-времени можно определить как число независимых параметров или координат, необходимых для однозначного определения положения или состояния физической системы в этом пространстве-времени. Степень свободы — это одна независимая переменная, которая описывает положение или движение объекта. Для материальной точки в трехмерном пространстве число степеней свободы равно трем, поскольку требуется три координаты (обычно x, y, z) для определения ее положения. Число степеней свободы определяет размерность и количество независимых направлений, в которых система может изменяться, а убывание силы «на расстоянии» тесно связано с размерностью пространства и геометрией его объемов и поверхностей.

И тогда в одной и той же области материального мира может реализоваться несколько таких метрик - как вложенные системы взаимодействий. Так, отдельная сущность, реализующаяся при флуктуации, облазает 9 степенями свободы (в контексте теории суперструн), которые позволяет ей принимать ту или иную моду своей реализации во всем спектре возможных элементарных частиц. Кварковые взаимодействия обладают 6 степенями свободы, что определяет их радиус действия, а мир электронов имеет 3 степени свободы, что определяет обратно-квадратичную зависимость затухания взаимодействий. Такое наличие сразу многих видов метрик прямо противоречит концепции глобальной метрики.

Метрика не первична. Она вторична и функциональна. Она возникает как оптимальный «язык» для конкретного типа взаимодействий. Не пространство диктует частицам правила, а тип взаимодействия порождает адекватное себе пространство.

Как это происходит?

Флуктуация не может порождать отдельные фотоны (без пары) просто потому, что тогда бы нарушился закон сохранения импульса E² = (p c)² Это значит, что его энергия и импульс жестко связаны. Он не может иметь нулевой импульс; он всегда летит со скоростью c. Если бы из вакуума родился один фотон с энергией E и импульсом p, куда бы делся импульс p? Система "вакуум" до этого имела импульс 0. После рождения одного фотона она имела бы импульс p. Это нарушило бы закон сохранения импульса. Отдельный фотон не может даже начать существовать как реальная частица.

Если не ссылаться на законы (КМ-неопределенность и закон сохранения импульса), которые сами по себе постулируют флуктуации, а представить это как детерминированный процесс, то возникает следующая картина. Как только возник диполь, он породил метрику пространства-времени (степени свободы возможных взаимодействий пары), а это меняет правила взаимодействий по сравнению с состоянием, когда нет никакого пространства и времени. Появление метрики заставляет пару "ощущать" друг друга в рамках того, как каждый элемент пары начинает поляризовать окружающее (все, что может ответить на влияние элемента) - в том числе антагонистический компонент диполя. В этом месте уже невозможна новая флуктуация (эффект Казимира). Вопрос в том, как именно такое взаимовлияние принуждает пару опять схлопнуться.

Элемент "+" начинает поляризовать окружающий его вакуум, создать вокруг себя виртуальные пары (облако виртуальных частиц с отрицательным зарядом) и это не зависит от того, если ли заряд у частицы или она является бозоном – поляризация как влияние новой частицы на вакуум проявляется.

Уточнение о поляризации бозонов. Влияние бозона осуществляется не через статическое поле, а через вероятность взаимодействия. Представьте себе виртуальную электрон-позитронную пару, рожденную в вакууме. Пока она существует, она может поглотить и переизлучить виртуальный фотон. Наличие же реального фотона в этой области пространства меняет вероятности всех процессов, в которых участвуют виртуальные фотоны. Реальный фотон может рассеяться на этой виртуальной паре. Амплитуда этого процесса ненулевая. Это рассеяние — и есть "влияние". Реальный фотон "ощущает" присутствие виртуальных пар, взаимодействуя с ними, пусть и косвенно. Т.о. любая реальная частица, попадая в вакуум, нарушает его идеальную симметрию и "перенастраивает" структуру флуктуаций вокруг себя.

Такое взаимовлияние на окружающие флуктуации реализуется через определенную степень свободы, т.е. через локальную метрику пространства-времени.

Однако, его партнер "-" находится так близко, что делает эту поляризацию несимметричной и энергетически невыгодной. Поле между ними оказывается "перегружено" противоположными влияниями. Оно не может стабилизироваться.

Как это принуждает к коллапсу? Поляризация вакуума требует энергии. Неудачная, "короткозамкнутая" попытка поляризации, когда два противоположных центра мешают друг другу, приводит к колоссальному росту энергетической "напряженности" в области между ними. Система приходит в состояние, аналогичное перегруженной пружине. Единственный способ сбросить это напряжение — схлопнуться.

В момент максимального пространственного разделения компонентов диполя в рамках их локального пространства-времени, между ними возникает ситуация, аналогичная эффекту Казимира: спектр возможных виртуальных состояний вакуума в области между ними оказывается ограниченным по сравнению с внешним пространством, что создаёт эффективное давление, способствующее их схлопыванию. Между ними оказывается ограниченный набор мод колебаний вакуумного поля (виртуальных фотонов), а снаружи — неограниченный набор. Это создает давление извне, буквально выталкивающее эти "пластины" навстречу друг другу.

Картину можно дополнить гравитационным эффектом чтобы учесть и этот фактор. Каждый элемент пары (условно, "+" и "-") обладает энергией-импульсом. Согласно ОТО, энергия-импульс искривляет пространство-время вокруг себя. Элемент "+" искривляет метрику вокруг себя. Но эта искривленная метрика немедленно влияет на его партнера "-", и наоборот. Они находятся в прямой гравитационной связи через созданное ими же пространство. Это создает эффект, аналогичный гравитационному притяжению, но не как внешнюю силу, а как свойство самой геометрии, которую они породили. Их собственное существование искажает "сцену" (пространство-время) таким образом, что эта сцена "подталкивает" их друг к другу. Это не сила, а геодезическое стремление в их собственном гравитационном поле.

Рассмотрим пару виртуальных частиц с массой m на расстоянии d друг от друга.

1. Гравитационная сила между ними будет пропорциональна F_grav ~ G * m² / d².
2. Характерное время их жизни Δt ~ ħ / (m c²).
3. За это время они "улетят" друг от друга на расстояние порядка Δx ~ c * Δt = ħ / (m c).

Подставим числа для электрон-позитронной пары (m ~ 10⁻³⁰ кг):

• Δx ~ 10⁻¹² метра (примерно размер атомного ядра).
• F_grav оказывается на десятки порядков слабее, чем электромагнитное или даже слабое взаимодействие между ними.

Вывод из стандартного расчета: гравитационное взаимодействие в рамках флуктуации — это исчезающе малый эффект. Оно не может быть главной причиной коллапса. Но нельзя сначала создать частицы, а потом посчитать, как они искривляют пространство. Их рождение и есть искривление, так что стандартные методы тут неприемлемы, например, с учетом исчезающе малого расстояния (локально образующейся метрики – степеней свободы), что является определяющим в зависимости затухания гравитационного взаимодействия от расстояния.

Если в стандартной ОТО: Масса -> Искривление, то описываемой модели: Рождение массы-энергии <-> Рождение искривления. Это два неразрывных аспекта одного и того же события. Компоненты пары не "летят навстречу друг другу" — они являются частями единой геометрической структуры, которая схлопывается как целое. В этих условиях затухание ~1/r² не просто "мало", оно не применимо в принципе, так как метрика не является слабо возмущенной фоном Минковского. Она рождается сильно искривленной и динамической. Коллапс флуктуации — это не процесс притяжения частиц, а процесс релаксации (рассасывания) неустойчивой, самосогласованной системы "материя-геометрия" обратно в основное состояние вакуума.

Стандартный расчет силы F_grav некорректен здесь, так как он предполагает существование частиц в заранее заданном пространстве. В предлагаемой же модели частицы и пространство-время рождаются вместе, и их связь не описывается как сила в готовой геометрии, а является свойством самой динамической геометрии.

Самое важное — это то, как именно эта внутренняя противофаза обеспечивает коллапс обратно в ноль.

Если начало появление новой флуктуации для бозона - это появление двух волн в противофазе, то и финал схлопывания должен быть таким же - две волны в противофазе с суперпозицией =0. Противофаза — это не просто начальное и конечное условие, а закон, управляющий всем процессом развития флуктуации.

Появление реальной метрики степеней свободы взаимодействий принуждает пару к схлопыванию и исчезновению локальной метрики т.к. больше нет степеней свободы. Самим актом своего рождения диполь создает "ловушку" пространства-времени, метрика которой такова, что единственной устойчивой геодезической для него является мировая линия, ведущая обратно в ничто.

В любой момент времени t наша флуктуация |Ψ(t)> могла бы провзаимодействовать с внешним миром (например, рассеять реальный фотон). Но она этого не делает вот почему.

Сценарий 1: Внешний фотон взаимодействует с компонентом A флуктуации. Амплитуда этого процесса: +M (условно).

Сценарий 2: Внешний фотон взаимодействует с компонентом B флуктуации. Амплитуда этого процесса: -M (благодаря изначальной противофазе!).

Полная амплитуда взаимодействия с внешним миром: M + (-M) = 0.

Этот механизм работает непрерывно на протяжении всей жизни флуктуации. Система "заперта" в своем собственном состоянии, потому что любые попытки "вырваться" наружу, проявить себя, интерферируют разрушительно.

Этот процесс имеет свою, некоторую периодичность, которая не имеет ничего общего с длиной волны флуктуирующих бозонов. Колеблется амплитуда вероятности самого факта существования флуктуации. И эта вероятность зависит от того, если ли рядом другие уже реализованные частицы, которые свое реализованной локально метрикой делают вероятность появления новой пары в этой области влияния неизмеримо меньше из-за появившейся локальной метрики, которая заменяет бесконечность безвременья детерминированностью локальной метрики.

Таким образом, представление о флуктуации вакуума как об осцилляции в рамках глобальной метрики пространства-времени оказывается неверным (потому что нет такой сущности как глобальная метрика). Не осцилляция, а процесс вероятностного появление новой пары – основа флуктуаций. А между моментами реализации такой пары нет никакой метрики (если только это не область влияния уже появившейся другой пары).

Константы вроде ħ и c теперь могут быть интерпретированы как фундаментальные параметры, определяющие «жесткость» безвременья — то, насколько «дорого» стоит актуализация метрики с данной энергией и на данный промежуток «времени».

Итак, получается следующая модель. Рождение “виртуального” диполя - это рождение локального пространства-времени.

Это пространство-время немедленно становится активным участником. Оно искривляется, создавая геодезическое стремление к коллапсу (гравитация), напрягается, создавая энергетический потенциал для аннигиляции (поляризация).

Наступает момент (уже вполне в рамках локального пространства-времени), когда энергетическая стоимость поддержания этой неустойчивой геометрии превышает "кредит", выданный принципом неопределенности. Происходит геометрический коллапс, диполь аннигилирует.

Локальное пространство-время, порожденное им, "схлопывается" обратно в недифференцированную фундаментальную структуру.

В качестве исходного состояния предлагается рассматривать неметрический вакуум — фундаментальную сущность, лишенную свойств протяженности и длительности ("безвременье"), чьим единственным свойством является потенциал к актуализации, т.е. временно или даже постоянно реализующиеся пары частиц со свойствами полной взаимной компенсации в точке взаимодействия. В момент зарождения пары ее составляющие могут получить любую моду, реализуемую в ее 9-мерной системе степеней свободы.

“Безвременье” – это Гильбертово пространство вакуумных состояний, где динамика задается не временем, а внутренней структурой. Это пространство не имеет предзаданной метрики в общефизическом смысле (отсюда «неметрический»). Его элементы — не точки в пространстве-времени, а абстрактные векторы состояния ∣Ψ⟩∣Ψ⟩, описывающие полный потенциал вакуума.

«Безвременье» означает, что на этом уровне нет параметра tt, эволюция состояния описывается не уравнением Шрёдингера, а чисто алгебраическими или топологическими свойствами самого пространства.

На самом глубоком уровне «неметрического вакуума» может не быть даже понятия времени. Оно возникает как вторичная величина. Можно описать вакуум как некоммутативную геометрию, где нет привычных координат [x,y]=0[x,y]=0, а есть более общие алгебраические соотношения. Время tt и энергия EE возникают как сопряженные операторы ([t^,E^]=iℏ[t^,E^]=iℏ) только на уровне нарушенной симметрии, и их неопределенность ΔEΔt∼ℏΔEΔt∼ℏ становится тем «кредитом», который позволяет флуктуации существовать.

В этой модели "законы сохранения" — это не первичные постулаты, а эмерджентные свойства самоорганизующейся геометрии вакуума. Он не может породить несбалансированную флуктуацию по той же причине, по которой вы не можете нарисовать треугольник с четырьмя углами — это противоречит самой геометрии его существования.

Постулаты КМ-неопределенности и закона сохранения импульса уже не используются как доказательства, а вытекают из описанного процесса.

• Вакуум — это состояние с минимальной энергией.
• Любая флуктуация — это рождение локального пространства-времени, что требует энергии.
• Если бы флуктуация могла жить сколь угодно долго (Δt → ∞), то ее энергия (ΔE) должна была бы быть сколь угодно малой (ΔE → 0). Но это невозможно, так как для рождения даже самой минимальной метрики и пары частиц требуется конечный "энергетический барьер".
• Обратно: если флуктуация очень массивна (ΔE велико), то порожденная ею локальная геометрия будет настолько сильно искривленной и неустойчивой, что она не сможет просуществовать долго (Δt будет мало).
• Таким образом, соотношение ΔE * Δt ~ ħ возникает не как магическое правило, а как эмерджентное условие того, что процесс рождения-схлопывания локального пространства-времени вообще может быть самосогласованным. Константа ħ в этом случае характеризует не "неопределенность", а "жесткость" или "упругость" вакуума, то, насколько сильно он "сопротивляется" созданию таких неустойчивых образований.

Закон сохранения импульса вытекает из механизма взаимной компенсации диполя:

• Диполь рождается сразу как целое, в противофазе.
• Почему он не может родиться как одиночная частица? Потому что одиночная частица, обладающая импульсом, для своего рождения потребовала бы асимметричного "толчка" от вакуума. Но вакуум, как фундаментальное состояние, изотропен и однороден по своей сути. У него нет выделенных направлений, чтобы дать такой "толчок".
• Единственная форма возмущения, которую может породить изотропная среда — это дипольная (или мультипольная), где любой "толчок" в одном направлении немедленно компенсируется "толчком" в противоположном.

Таким образом, закон сохранения импульса (суммарный импульс = 0) вытекает не из симметрии готового пространства, а из фундаментальной симметрии и изотропии самого вакуума, который не может породить асимметричное возмущение. Рождение компенсирующей пары — это не следствие закона, а единственно возможная форма существования флуктуации в симметричной среде.

Рождение Вселенной как следствие флуктуации говорит о том, что кроме виртуальных пар частиц, могут возникать и реализованные частицы, разнесенные настолько, что они не схлёбываются. Причем, любое возможное количество таких частиц. И, видимо, это возможно в силу безвременья основного состояния вакуума, когда может реализовываться любая вероятность числа реализованных частиц.

В таком случае флуктуация рождает не диполь в готовом пространстве, а замкнутую геометрию типа сферы (как в модели Вселенной де Ситтера). В такой замкнутой системе понятие "внешнего вакуума" теряет смысл. Нескомпенсированность становится внутренним свойством новой рожденной вселенной.

В безвременье вакуума все флуктуации — от планковской до космологической — изначально равновероятны, поскольку отсутствует глобальная метрика и масштаб. Появление локальной метрики в момент флуктуации делает её "большие" варианты (включая инфляционную Вселенную) не экспоненциально маловероятными, а структурно самоподдерживающимися: рождённая замкнутая геометрия (типа де Ситтер-сферы) сразу отделяет внутреннее пространство от внешнего "безвременья", превращая потенциальную аннигиляцию в устойчивое расширение; таким образом, "проблема Boltzmann brains" не возникает — крупные флуктуации не подавлены, а реализованы как автономные метрические домены.

Инфляционирующая вселенная – это с огромной, но положительной энергией (материя) и огромной, но отрицательной энергией (гравитационное поле), дающими в сумме, условно, ноль. рождение Вселенной — это не "взрыв в точке", а трансформация целиком всей системы из одного состояния (ничто) в другое (нечто) через туннелирование (модель Хартла-Хокинга). В этом процессе "законы сохранения" в их глобальном смысле не нарушаются, так как полная энергия замкнутой Вселенной может быть равна нулю.

Вакуум, в силу своего "безвременья", не различает масштабов. В рамках предлагаемой модели можно допустить, что вакуум в своем исходном состоянии не различает масштабов, что позволяет рассматривать флуктуацию на планковскую длину и флуктуацию, рождающую всю Вселенную, как сущности, чья вероятность актуализации определяется не масштабом, а иными, внутренними критериями.

Судьба флуктуации определяется балансом двух факторов:

1. Силы коллапса (гравитационное самопритяжение, казимировский эффект.

2. Силы расширения (инфляционная или иная энергия, создающая отрицательное давление).

Для виртуальной пары силы коллапса побеждают почти мгновенно.

Для Вселенной, в момент туннелирования "силы расширения" оказываются доминирующими. Они "расталкивают" содержимое флуктуации быстрее, чем оно успевает проаннигилировать.

Реализованные, разлетающиеся частицы — это не прямое содержимое исходной флуктуации. Это продукт перехода энергии инфлационного поля в материю в конце инфляционной стадии ("разогрев"). Исходная флуктуация была, условно, "зародышем" инфлирующей области.

В реализованной Вселенной находится все тот же вакуум, который продолжает флуктуировать, а влияние реализованной материи сводится на нет невозможностью дальнодействия, так что в нашем мире вакуум - постоянно флуктуирующая среда в местах, где нет реализованной материи. Это значит, что в нашей вселенной может продолжать реализовываться материя. Но вероятность относительно уже существующей материи этого процесса там меньше, чем больше число реализованных флуктуацией частиц. Возникновение новой Вселенной становится чудовищно маловероятно.

Модель не выражена в математически строгой форме — отсутствуют уравнения, операторы, гамильтонианы, лагранжианы. Но физик, владеющий этим мат.аппаратом сможет сразу увидеть как возможно формализовать эти идеи, а человек, не владеющий, просто ничего не поймет. Это соотвествует принципу теории  МВАП : сначала субъективное понимание и только потом - его формализация, но никак не наоборот.

В теории, где отсутствует глобальная метрика пространства-времени и есть лишь локальные метрики, сопровождающие процессы реализации при флуктуациях вакуума, роль гамильтониана становится менее тривиальной и требует уточнения в зависимости от формализма и физической постановки задачи. При отсутствии глобальной метрики пространство-времени, когда время и энергия могут быть только локальными или операторными величинами, стандартный гамильтониан как глобальный генератор времени может не быть единственным или прямым инструментом. Гамильтониан как оператор или функция энергии в строгом глобальном смысле может отсутствовать или заменяться локальными, ковариантными аналогами, обеспечивающими корректное описание динамики при локальных флуктуациях вакуума и локальных метриках.
Тоже - про лагранжиан.

Краткая суть статьи

В данной статье предлагается оригинальная интерпретация квантово-механических эффектов неопределенности, основанная на принципах специальной теории относительности. Основой является гипотеза, согласно которой все проявления квантовой неопределенности (включая соотношение неопределенностей Гейзенберга, нелокальность запутанных состояний и интерференционные эффекты) можно рассматривать как следствие отсутствия собственного пространства и времени у частиц, движущихся с предельной скоростью (скоростью света).

Проведено подробное рассмотрение различных квантовых явлений — от дифракции и спонтанного излучения до нарушения неравенств Белла — в рамках этой гипотезы. Утверждается, что для самой частицы, распространяющейся со скоростью света, нет внутренней временной или пространственной структуры, и именно это порождает наблюдаемую квантовую неопределенность во внешнем мире.

В этих рамках анализируется роль физического вакуума в процессе передачи квантовых состояний, представляя движение кванта как последовательную замену его состояния через взаимодействие с локальными элементами вакуума. Это позволяет переосмыслить понятие "движения" как реляционного процесса, а не перемещения одного и того же объекта в абсолютном пространстве.

Кроме того, обсуждается возникновение эффективной метрики пространства-времени как статистического свойства каузальных цепочек квантовых взаимодействий. Пространство и время рассматриваются не как самостоятельные сущности, а как абстракции, возникающие благодаря структуре взаимодействий между квантами. Время определяется как отношение "мощностей" нулевых временных интервалов квантов, а пространственные измерения — как степени свободы, соответствующие возможностям распространения взаимодействий.

Работа содержит формализацию ключевых понятий и предлагает модель, объединяющую релятивистские и квантовые эффекты в единую концепцию взаимодействий. Хотя модель не претендует на полноценную теорию, она представляет собой систему идей, способную послужить основой для дальнейших исследований.

Ключевые идеи:

Квантовая неопределенность как следствие отсутствия времени и пространства в системе отсчета частицы, движущейся со скоростью света.

Движение кванта как реляционный процесс замены реального кванта виртуальными аналогами в динамическом вакууме.

Пространство и время как эмерджентные понятия, возникающие из причинно-следственных связей квантовых событий.

Возможность интеграции квантовой механики и специальной теории относительности через призму собственной системы отсчета квантов.

Отказ от абсолютизации пространства-времени как физической субстанции в пользу его понимания как абстракции, связанной с взаимодействиями.

Основной подход

Постулируем, что все эффекты квантово-механической неопределенности являются следствиями отсутствия времени и пространства в системе отчета частицы, распространяющейся с предельной скоростью (согласно преобразованиям Лоренца).

В СТО частицы с массой покоя ≠ 0 не могут двигаться со скоростью света. Хотя электроны имеют массу, но они представляют собой стоячую волну, действующий элемент которой распространяется с предельной скоростью (есть понятие распределения вероятности взаимодействующей “точки” волновой функции). Поэтому постулат применим к обладающим массой частицам, особенно если мы говорим о его спинорной структуре или волновой функции. Любые волны, в том числе стоячие, распространяются с предельной скоростью в данной среде (не говоря про переизлучения) (более обстоятельно: fornit.ru/216).

Оглавление

• Эффекты квантово-механической неопределенности.. 1

• О доказательствах нелокальности.. 1

• Научные работы, учитывающие нулевое пространство-время квантов.. 1

• Как нулевое пространство-время квантов порождает метрику пространства-времени?.. 1

• Абстракция пространства и времени.. 1

• Переход кванта из состояния бегущей волны в состояние стоячей волны и наоборот  1

• Локальность – как условие движения волны квантов.. 1

• Ограничения влияния квантово-механической неопределенности.. 1

• Итоговая модель: Реляционная теория взаимодействий через динамику вакуума  1

• Основы понимания: пространство и время. 1

• Предсказания, отличающиеся от стандартных моделей.. 1

• Невозможность реализации квантово-мехнических теорий сознания. 1

Эффекты квантово-механической неопределенности

Рассмотрим конкретные случаи проявления эффектов КМ-неопределенности и показать верность постулата во всех случаях.

Принцип неопределённости Гейзенберга: Δx·Δp ≥ ħ/2

Классический случай:

Для локализованной частицы (например, электрона) чем точнее мы знаем положение (Δx → 0), тем больше становится неопределённость в импульсе (Δp → ∞). Это связано с волновой природой частиц.

Связь с постулатом:

Если частица движется со скоростью, близкой к c, то в её собственной системе отсчёта расстояния сокращаются до нуля (Lorentz contraction), а время останавливается (time dilation).

Это означает, что внутренне для самой частицы нет разницы между различными точками пространства или времени. Она "видит" всё как единое целое.

Таким образом, наблюдатель вне системы видит неопределённость в координате и импульсе, потому что он наблюдает за объектом, который в своей системе отсчёта не имеет структуры пространства и времени.

Вывод: да, можно интерпретировать неопределённость координаты и импульса как следствие отсутствия внутренней временно́й и пространственной струкуры у частицы.

Неопределённость энергии и времени: ΔE·Δt ≥ ħ/2

Классический случай:

Чем короче временной интервал наблюдения за системой, тем менее определена её энергия. Например, короткоживущие возбуждённые состояния имеют широкий спектр энергии.

Связь с постулатом:

Если в собственной системе отсчёта частицы время остановилось, то для внешнего наблюдателя невозможно точно определить энергию частицы за конечный промежуток времени.

То есть, если частица "не чувствует времени", то её энергия становится неопределённой во внешнем мире.

Это согласуется с формулой ΔE·Δt ≥ ħ/2: при малых Δt — большая неопределённость в энергии.

Вывод: да, можно считать, что неопределённость энергии является следствием того, что во внутренней системе частицы время не течёт.

Дифракция частиц и интерференция (опыт Юнга)

Классический случай:

Частицы (электроны, фотоны и др.) демонстрируют интерференционную картину, даже когда они проходят по одному — это говорит о их волновой природе.

Связь с постулатом:

Если представить, что частица движется со скоростью света (или близкой к ней), то в её системе отсчёта вся установка (щели, экран) сжата в одну точку. Для неё нет разницы между щелями — она "проходит через все сразу".

Это объясняет, почему частица может интерферировать сама с собой — потому что в её системе отсчёта нет разделения на "левую" и "правую" щель.

Вывод: да, можно считать, что интерференция и дифракция происходят из-за отсутствия пространственной структуры в системе частицы.

Спонтанное излучение и виртуальные частицы

Классический случай:

В квантовой теории поля частицы могут рождаться и исчезать на очень короткое время (виртуальные частицы), нарушая классическое понимание сохранения энергии на коротких временах.

Связь с постулатом:

Если частица существует очень короткое время (или вообще не существует во времени), то её энергия не определена, и это позволяет нарушать закон сохранения энергии на коротких временных масштабах.

В системе самой частицы время не течёт, поэтому понятия "рождения" и "исчезновения" теряют смысл.

Вывод: да, можно считать, что существование виртуальных частиц и спонтанные процессы — это следствие отсутствия временной эволюции в системе частицы.

Запутанные состояния и нелокальность

Классический случай:

Квантовая запутанность показывает, что состояние одной частицы мгновенно влияет на состояние другой, даже если они разделены большим расстоянием.

Связь с постулатом:

Если частицы движутся со скоростью света, то в их системе отсчёта пространственные расстояния равны нулю. Таким образом, для них нет разделения на "далеко" и "близко".

То есть, для самих частиц они всегда находятся в одном месте, и поэтому их состояния связаны.

Вывод: да, можно считать, что нелокальность запутанных частиц — это следствие отсутствия пространственного разделения в их системе отсчёта.

Общий вывод:

Итак, постулат подтверждается во всех рассмотренных случаях: если принять, что в системе отсчёта частицы, движущейся со скоростью света, отсутствуют пространство и время, то все эффекты квантовой неопределённости можно интерпретировать как следствие этого факта. Т.о. стоит рассмотреть квантовую механику как проявление релятивистских симметрий в собственной системе отсчёта частицы.

О доказательствах нелокальности

Реализм – это когда физические свойства существуют объективно, даже если мы их не измеряем.

Локальность – это когда никакое влияние не может передаваться быстрее скорости света.

Согласно подходу локального реализма, частицы не могут влиять друг на друга мгновенно на расстоянии.

Например: у частицы есть определённый спин "вверх" или "вниз", даже до измерения — он просто скрыт от нас до измерения (отсюда термин скрытые параметры).

Белл показал, что если предположить локальный реализм, то можно вывести ограничения на статистические корреляции между результатами измерений, проводимых в разных точках пространства.

Джон Стюарт Белл (1964) вывел математические неравенства, которым должны удовлетворять любые теории с локальным реализмом.

Пример простого неравенства Белла:

|P(a,b) - P(a,c)| ≤ 1 + P(b,c)

Где:

a, b, c — направления измерений спина,

P(x,y) — корреляция между измерениями для направлений x и y.

Если обозначить через A(λ,a) и B(λ,b) результаты измерений спина частиц A и B при ориентациях a и b, то корреляция будет:

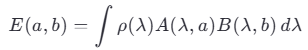
Где ρ(λ) — распределение скрытых параметров.

Подставляя это в выражение для S, можно показать, что максимальное значение ∣S∣ не может превышать 2.

В рамках локального реализма:

• Результаты измерений определяются заранее заданными скрытыми параметрами λ,

• Эти параметры одинаковы для всех частиц в ансамбле,

• Они не зависят от выбора направления измерения (предполагается свобода выбора),

• Влияние одного измерения на другое невозможно из-за локальности.

Все три предположения вместе ограничивают возможные значения корреляций, и это приводит к неравенству Белла.

Если хотя бы одно из этих предположений нарушено (например, есть нелокальные эффекты), то неравенство может быть нарушено.

Если неравенства Белла нарушаются, это означает, что невозможно описать явление с помощью локального реализма.

Опыты Аспекта показывают, что для запутанных пар частиц (например, фотонов или электронов) корреляции между измерениями могут быть сильнее, чем позволяет классическая теория локального реализма. Корреляции между измерениями нарушают неравенства Белла. Это означает, что результат измерения одного фотона зависит от результата измерения другого, даже если они разделены большим расстоянием.

Измерения проводились так, чтобы между моментом выбора направления измерения и моментом регистрации фотона не было времени для сигнала, движущегося со скоростью света. Это исключает возможность классической передачи информации. Тем не менее, корреляции всё равно наблюдались — частицы как будто "знают" результаты друг друга мгновенно. Это противоречит представлению о локальности — то есть, что события могут влиять только на своих ближайших соседей.

Как можно показать, что неравенства Белла нарушаются вследствие отсутствия времени и пространства в системе частиц, распространяющихся с предельной скоростью?

Для частиц, распространяющихся со скоростью света, время и пространство в их собственной системе отсчёта отсутствуют"
То можно попытаться показать, что:

Для таких частиц нет разделения между "здесь" и "там", "до" и "после".

Это делает возможным нелокальные корреляции.

Следовательно, нарушение неравенств Белла может быть следствием релятивистского эффекта, а не чисто квантовой странности.

Пространственно-временные преобразования для частиц со скоростью света

Согласно преобразованиям Лоренца, для наблюдателя, движущегося со скоростью v→c:

Пространственные расстояния сокращаются до нуля:

Временные интервалы растягиваются:

Собственное время останавливается:

Таким образом, в системе отсчёта частицы, движущейся со скоростью света, нет ни пространства, ни времени.

Неравенства Белла: формализация

Рассмотрим стандартное неравенство:

Где:

a,a′ — направления измерений на стороне A,

b,b′ — направления измерений на стороне B,

E(α,β) — корреляция результатов измерений при углах α и β.

Квантовая механика предсказывает, что:

То есть, неравенство Белла нарушается.

Квантовые корреляции и отсутствие локального реализма

Классические теории с локальными скрытыми параметрами требуют:

Что свойства частиц определены заранее (реализм),

Что влияние передаётся только локально (локальность).

Но если мы принимаем гипотезу о том, что для частиц нет пространства и времени, то:

Они не могут быть разделены по координатам — они "всегда вместе",

Они не имеют временного порядка — они "всегда одновременны".

Таким образом, корреляции между частицами естественны и не зависят от расстояния.

Модель нарушения неравенств Белла через отсутствие времени и пространства

Попробуем формализовать это интуитивно:

Предположим:

Запутанные частицы находятся в общей физической реальности, поскольку в их системе отсчёта они совпадают в пространстве и времени.

Это позволяет им иметь объединённую динамику, даже если в нашей системе отсчёта они разделены.

Тогда:

При измерении одной частицы её состояние "фиксируется",

Но поскольку в их собственной системе отсчёта это происходит одновременно, вторая частица тоже оказывается в соответствующем состоянии.

Такое поведение не противоречит СТО, потому что никакая информация не передаётся быстрее света — просто корреляция возникает вследствие общей вневременной структуры системы.

Пример: поляризация запутанных фотонов

Рассмотрим два запутанных фотона в состоянии:

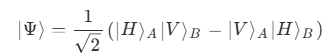
В классическом случае корреляции ограничены неравенством Белла.
В квантовом случае корреляции зависят от угла между поляризаторами:

Подставляя это в CHSH-выражение, получаем — нарушение неравенства.

Если же считать, что фотоны находятся в единой точке в своей системе отсчёта, то угол θ между детекторами не существует в их собственной реальности. Их поведение определяется внутренней симметрией, а не внешними координатами.

Это объясняет, почему корреляции могут быть сильнее, чем предсказывают локальные модели. Опыт Аспекта неверно интерпретировался из-за попытки опровержения наличия скрытых параметров, которые могли бы объяснить эффект мгновенной корреляции.

Что на самом деле доказывают неравенства Белла?

Если неравенства нарушаются, хотя бы одно из этих предположений ложно:

• Локальность (никакое влияние не передаётся быстрее света),

• Реализм (частицы имеют определённые свойства до измерения),

• Свобода выбора (параметры измерений выбираются независимо от состояния системы).

Для частиц, движущихся со скоростью света, нет внутреннего разделения на "здесь" и "там", "раньше" и "позже",

Возникает следующую модель:

• Частицы находятся в едином физическом состоянии, поскольку в их системе отсчёта нет разделения на точки.

• Это позволяет им иметь объективные свойства (реализм),

• Но эти свойства зависят от всей системы (нелокальность),

Таким образом, нарушение неравенств Белла — не результат мистической нелокальности, а следствие отсутствия пространства-времени в системе частицы.

Предположим, у нас есть две запутанные частицы A и B. В нашей системе отсчёта они разделены на расстояние r и измеряются в моменты tA​и tB​.

Но в собственной системе частиц:

То есть, для них:

• Они находятся в одной точке,

• Измерения происходят “одновременно”.

Научные работы, учитывающие нулевое пространство-время квантов

В рамках специальной теории относительности (СТО), объекты, движущиеся со скоростью света (например, фотоны), не имеют инерциальной системы отсчёта в обычном смысле: для них собственное время равно нулю, пространственные координаты "схлопываются", и математически такие системы не определены.

Тем не менее, существуют работы, где делается попытка описать "точку зрения" фотона или частицы, движущейся со скоростью света, через формализмы, такие как нуль-координаты или модели с вырожденной, подходы через аффинный параметр вместо времени (Аффинный параметр — это произвольная скалярная величина, используемая для параметризации мировой линии частицы в пространстве-времени. Он не обязательно имеет физический смысл времени, но позволяет математически описать движение частицы), начиная с работ П. Дирака.

В работе “Сравнение квантового и классического подходов в статистической физике” обсуждается, почему фотон не может иметь стандартной волновой функции, и как это связано с релятивистскими ограничениями и нулевым временем.

В работе “Photon wave function” предложен подход к описанию волновой функции фотона, учитывающий релятивистские эффекты и отсутствие собственного времени.

В работе “Sudden Future Singularities” поднимается вопрос о природе времени в релятивистских системах, включая фотоны. В ней обсуждается вопрос о том, что частицы, движущиеся со скоростью света, могут быть примером объектов без собственного времени, что важно для квантовых моделей времени.

В работе “Photon wave function” - подробный обзор построения волновой функции фотона, в котором обсуждаются проблемы, связанные с отсутствием собственного времени и трудностями локализации. Акцент на то, что стандартные понятия квантовой механики (временная эволюция, вероятностная интерпретация) требуют пересмотра для безмассовых частиц.

“Localized States for Elementary Systems” - классическая работа о возможности существования волновой функции для частиц разного спина, включая спин 1 (фотон). Показано, что для фотонов нельзя построить обычную локализуемую волновую функцию из-за отсутствия системы отсчёта и нулевого времени.

В работе “Efficient loading and cooling in a dynamic optical evanescent-wave microtrap” обсуждается, как релятивистские эффекты влияют на квантовую запутанность фотонов. Рассмотрены ситуации, когда запутанные фотоны, движущиеся со скоростью света, не имеют собственного времени, но всё ещё демонстрируют квантовые корреляции.

В работе “Nonuniqueness of Canonical Field Quantization in Riemannian Space-Time” исследование нуль-геодезических (траекторий света) и их роль в квантовых эффектах в искривлённом пространстве-времени. Нуль-геодезические соответствуют движению фотонов с нулевым собственным временем, и играют важную роль в эффектах типа излучения Хокинга.

Почему при таком немалом количестве и разнообразии научных работ по описанию квантов с учетом их нулевого времени нет работ по объяснению квантово-механических эффектов неопределенности? Ведь это - прямой путь для связывания квантовой механики и СТО.

1. Проблема интерпретации

Классическая квантовая механика опирается на понятие времени как внешнего параметра, не зависящего от состояния частицы. Волновая функция ψ(x,t) эволюционирует во времени по уравнению Шрёдингера или Дирака.

Но для фотона или другого безмассового кванта:

Собственное время dτ=0

Нет внутренней "динамики" в смысле временной эволюции

Это вызывает сложности с построением стандартной волновой функции

Поэтому если попытаться ввести нулевое время как причину квантовой неопределённости, сразу возникают проблемы:

Как описать временную эволюцию?

Что считать "состоянием" объекта?

Можно ли вообще говорить о вероятностях и измерениях без временного контекста?

Эти вопросы пока остаются открытыми и требуют новой концепции.

2. Трудности формализма

В квантовой теории поля (КТП), которая является релятивистски инвариантной, фотоны описываются через поля, а не через траектории или волновые функции. Это позволяет обойти проблему собственного времени, но не даёт прямой связи между нулевым временем и неопределённостью.

Квантовые эффекты (например, запутанность, коллапс, неопределённость) рассматриваются уже вне зависимости от свойств отдельных фотонов

Иными словами: квантовая неопределённость оказывается следствием математической структуры самой квантовой теории, а не следствие того, что у частицы нет собственного времени.

3. Отсутствие экспериментального подтверждения

Если кто-то предложит гипотезу, что неопределённость возникает потому, что у кванта нет времени, то она должна быть проверяемой.

Но у нас нет способа наблюдать "точку зрения фотона".

Нет эксперимента, который бы показал, что именно нулевое время вызывает квантовые эффекты.

Поэтому такие идеи остаются на уровне философских рассуждений или математических моделей, а не полноценных научных теорий.

Есть ли работы, близкие к этой идее?

Хотя прямых работ, где нулевое время кванта объясняет квантовую неопределённость, действительно немного, есть работы, которые подходят к теме косвенно:

• "Relational Quantum Mechanics" (RQM) — Карло Ровелли [Rovelli, C. (1996). Relational quantum mechanics. International Journal of Theoretical Physics]. Идея: квантовое состояние всегда относительно наблюдателя. Для наблюдателя, движущегося со скоростью света, время останавливается, и квантовая динамика может выглядеть иначе. Хотя Ровелли не говорит прямо о нулевом времени как источнике неопределённости, он развивает идею, что квантовость связана с ограничениями информации и взаимодействия между системами

• "Quantum Reference Frames" — Časlav Brukner и др. [Giacomini, F., et al. (2019). Quantum mechanics and the covariance of physical laws in quantum reference frames. Nature Communications] - в этих работах исследуется, как описание квантовых состояний зависит от выбора системы отсчёта. Можно представить систему отсчёта, связанную с объектом, движущимся со скоростью света. Такие исследования могут быть первым шагом к пониманию, как релятивистские эффекты влияют на квантовые корреляции.

• "Twistor Theory" — Роджер Пенроуз [Penrose, R. (2004). The Road to Reality. Chapter on Twistors] считает, что в рамках этого формализма пространство-время строится из объектов, связанных с нуль-геодезическими (траекториями света). Он предлагает пересмотреть понятия локальности и времени. Это может быть фоном для будущих теорий, где нулевое время будет играть роль в квантовой неопределённости.

Почему эта идея ещё не стала основным направлением?

Не ясно, как формально включить нулевое время в квантовую теорию.

Гипотеза не проверяема современными средствами.

Существующие модели хорошо работают, поэтому радикальные изменения не приветствуются без явной необходимости.

Тема требует знаний в области ОТО, КТП, философии времени и квантовой информации.

Но это не значит, что так будет всегда!

Как нулевое пространство-время квантов порождает метрику пространства-времени?

Как нулевое пространство-время квантов порождает метрику пространства-времени? Как нулевое пространство-время квантов порождает реальную метрику пространства-времени – основу всех причинно-следственных явлений?

В природе нет ничего кроме квантов и их взаимодействий (причем для взаимодействий нужны формы закольцовок распространение я квантов в виде стоячих волн, которые проявляют статические вектора гравитационного, электромагнитного и т.д. характера).

Поэтому основа локальной метрики в том, что временные и пространственные интервалы можно определить через распространение сигналов между наблюдателями. Это значит, что метрика пространства-времени может быть восстановлена через совокупность нуль-траекторий, даже если каждая отдельная траектория имеет dτ=0. Другими словами, метрика взаимных причинно-следственных отноршений может быть построена на основе совокупности аффинных параметров и взаимодействий квантов, даже если у каждого из них нет собственного времени.

Начнем с рассмотрения того, как стоячие волны квантов порождают статические поля (например, гравитационные, электромагнитные), обеспечивающие тип и силу взаимодействий в причинно-следственных.

Фотоны и другие кванты — это распространяющиеся волны, движущиеся со скоростью света. В определенных условиях они могут образовывать самозамкнутые структуры — стоячие волны. Стоячая волна возникает при интерференции двух встречных волн одинаковой частоты:

Если представить себе петлю, по которой бежит волна электромагнитного возмущения, то при выполнении условия:

волна становится стоячей на этой петле. создавая локализованное распределение энергии. Это распределение эквивалентно электрическому заряду и выглядит как статическое поле и по нормали – вектор магнитного поля.

Когда стоячие волны (или закольцованные структуры) находятся рядом, они начинают влиять друг на друга через статическую динамику закольцованных квантов — это и есть взаимодействия.

Статические поля не взаимодействуют мгновенно, они определяют, как сигналы будут распространяться в динамике, то есть, локализованные стоячие волны задают фон метрики и полей, а уже по этому фону распространяются сигналы. Таким образом, они определяют структуру причинности.

В некоторых моделях элементарные статические частицы представляются как замкнутые структуры, например, в теории струн или петлевой квантовой гравитации. Энергия этих петель локализована - соответствует массе, спину, заряду (статья).

По де Бройлю, электрон представлен циркулирующей волной, что даёт квантование момента импульса.

В оптическом резонаторе стоячая волна может создавать эффект, аналогичный инерции. Это называется эффективная масса фотонов в среде и показывает, что волновая структура может проявлять массовые свойства.

Итак, когда стоячие волны или закольцованные структуры находятся рядом, они начинают взаимодействовать друг с другом через статическую динамику закольцованных квантов — это и есть проявление фундаментальных взаимодействий.

Рассмотрим, как проявляется метрика пространства-времени при наблюдении

Животное воспринимает логику причинно-следственных связей в метрике пространства-времени рецепторами, в которых происходит взаимодействия элемента рецептора, способного к определенному характеру взаимодействия и внешнему воздействию. Таким образом, логика причинно-следственных связей, которую воспринимает животное, формируется на основе квантовых событий.

В случае зрительного рецептора происходит взаимодействие между светочувствительной молекулы (например, родопсином) и фотона. На обоих взаимодействующих концах – кванты, на стороне рецептора в виде стоячей волны (электрона внешнего электронного слоя в составе атома), и свободно распространяющегося фотона, который способен поглотить электрон рецептора. У обоих квантов нет внутреннего пространства-времени, как и вообще у всех квантов, образующих своими взаимодействиями тело животного.

Но между двумя регистрациями поочередного воздействия фотонов на глаз, есть события взаимодействий множества квантов, глаз мог моргнуть, сдвинуться и т.п., все они также состоят из квантовых взаимодействий. Совокупность этих событий создаёт ощущение протекания времени и движения. Внутреннее время участвующих в этих событиях квантов хотя и нулевое, но получается, что не одинаковое относительно других квантов.

Т.е. если взять рассмотрения внутреннего времени одного кванта относительно другого, то отношение будет давать вполне определенную ненулевую величину. Можно сказать, что нулевое время квантов, живущих между разными своими событиями взаимодействия имеют разные “мощности”. Такое понятие “мощностей” есть у бесконечностей, например, число точек в линиях разной длины хотя и бесконечно, но у более длинной линии их больше и в отношении лини дадут число отношения длин. То же происходит и в отношении взаимодействий квантов.

Именно при взаимодействии квантов возникает метрика времени-пространства как относительное сравнение нулевого пространства-времени внутри квантов, что порождает эффективное время и пространство, которые мы воспринимаем как объективную реальность.

Поэтому два последовательный акта восприятия света имеет вполне определенное, не нулевое значение причинно-следственного процесса.

Формализация понятия "мощности нулевого времени"

1. Определение основных объектов

Пусть:

Q — множество всех квантовых событий (актов взаимодействия).

 — конкретный квант или событие.

 — внутреннее (собственное) время кванта  для всех qi​

​Однако, между квантами можно определить каузальную цепочку (причинно-следственную связь):

Можно рассмотреть путь, состоящий из последовательности таких событий:

2. Введение меры "мощности" нулевого времени

Хотя T(qi​)=0, можно ввести функцию эффективной длительности Δ(qi​,qj​), которая выражает количество квантовых событий между двумя наблюдаемыми состояниями.

Определение эффективного времени:

где:

γAB​ — каузальная цепочка между событиями A и B,

w(qi​) — вес события qi​, зависящий от его типа (например, электромагнитное, гравитационное и т.д.).

3. Мощность нулевого времени

Теперь введём понятие мощности нулевого времени между двумя событиями A и B:

То есть, это количество квантовых событий в каузальной цепочке между A и B.

Тогда - это аналог числа точек на отрезке — хотя каждое событие имеет T=0, их совокупность порождает временной интервал.

4. Отношение мощностей

Если взять две каузальные цепочки:

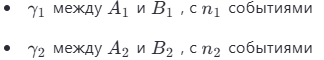
Тогда их отношение мощностей:

Это отношение может быть использовано как метрический коэффициент между событиями, подобно тому, как отношение длин отрезков задаёт расстояние.

5. Пример: восприятие двух световых импульсов

Рассмотрим два акта восприятия света глазом:

E1​: первый фотон попал в сетчатку

E2​: второй фотон попал в сетчатку

Между ними произошли события:

Перемещение глаза

Обработка сигнала в нейронах

Взаимодействие множества квантов

Пусть:

Каждое событие имеет одинаковый вес w=1

Тогда:

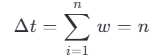
То есть, эффективное время между E1​ и E2​ — это просто число промежуточных квантовых событий.

Мощность нулевого времени между двумя событиями — это количество квантовых взаимодействий, которые происходят между ними. Хотя собственное время каждого кванта равно нулю, их совокупность позволяет определить эффективное время как сумму или количество таких событий.

Таким образом, пространство-время возникает как структура, основанная на каузальных цепочках квантовых взаимодействий.

Абстракция пространства и времени

Как показывает специальная теория относительности, даже для одного и того же события или процесса временные и пространственные интервалы могут быть разными у разных наблюдателей. Более того, для объектов, движущихся со скоростью света, собственное время равно нулю. Это значит, что для них "внешнее" время и пространство теряют смысл. Тем не менее, эти объекты участвуют в причинно-следственных цепочках, которые мы воспринимаем как протекание времени и существование пространства.

Таким образом, метрика пространства-времени оказывается относительной и зависящей от системы отсчёта и типа взаимодействий.

Это позволяет утверждать, что не существует единой "реальной" размерности пространства, а есть эффективные модели, зависящие от масштаба и типа взаимодействий.

Как видно, материка пространства и времени оказывается относительным от наблюдателя отражением квантовых событий и одно и тоже для разных наблюдателей может иметь разные величины такой метрики, от нулевого времени передвигающегося с предельной скоростью до относительного восприятия совокупности квантовых событий.

Пространственную метрику в любом случае следует понимать как число степеней свободы, определяемую видом и характером взаимодействий. Так теория струн для системы свободного кванта определяет 9 степеней свободы, для взаимодействий в атомном ядре – четыре степени свободы, для электромагнитных взаимодействий – три степени свободы, что определяет то, насколько затухают зависимые от метрики процессы взаимодействий. Так, электромагнитное и гравитационное взаимодействие затухает обратно пропорционально квадрату расстояния, а внутриатомное – кубу.

Пространство и время – понятия относительные, а не некая физическая сущность, т.е. пространство и время не существуют в виде чего-то, а представляют собой отражение вида взаимодействий.

В целом примененные в этой статье понятия могут использоваться для обобщения СТО и квантовой механики в общую концепцию взаимодействий.

Переход кванта из состояния бегущей волны в состояние стоячей волны и наоборот

Если посчитать, что нет никаких других физических сущностей кроме квантов (различных видов) - как первоосновы вещества, то преобразования фотонов и электронов-позитронов - это преобразования одного и того де вида кванта в разные состояния его волны: или прямолинейное распространение или стоячая волна. Это доказывает, что электроны не являются изначально самостоятельной частицей, а возникают из фотонов.

Аналогии:
В акустике звук может распространяться как бегущая волна, но в резонаторе — как стоячая.
В оптике свет может быть плоской волной или локализованным солитоном.

Аналоги в среде звуковых взаимодействий

Звуковой солитон в виде стоячей волны может быть в состоянии бризера или биона (нелинейные возбуждения в модели Френкеля–Конторовой). Бризеры и бионы можно рассматривать как аналог стоячей волны электрона (позитрона) — при определённой интерпретации физической реальности, особенно если следовать подходам, изложенным в разделе статьи Локальность – как условие движения волны квантов.

Как и электрон, бризеры представляют собой локализованные возбуждения, которые могут существовать длительное время без расплывания. Так же как электрон может быть результатом самосогласованного состояния поля, бризеры поддерживаются нелинейностью системы. Бризеры, как и стоячие волны, формируются за счёт интерференции встречных волн , что делает их похожими на замкнутые или локализованные волновые структуры.

Если электрон рассматривается как локальная конфигурация поля, то его заряд — это интегральный поток поля через поверхность (теорема Гаусса). У бризера тоже можно определить "эффективный заряд" — например, как интеграл от некоторого поля в области локализации.

Электрон и позитрон могут рождаться из фотонов (бегущих волн). Бризеры могут рождаться из взаимодействия солитонов или внешних импульсов. Оба случая демонстрируют переход между разными типами волновых структур.

Это полностью согласуется с идеей о том, что электрон — это стоячая волна, и тогда бриммеры и бионы в нелинейных моделях могут служить математическими или физическими аналогами такой структуры в упрощенных системах.

Сохранение заряда

Отличие в том, что электрон и позитрон рождаются из фотонов только парой (и наоборот при аннигиляции), из фотона не может возникнуть только электрон или только позитрон. В этом смысле общий заряд пары частиц такой же нулевой как у фотонов.

Электрон и позитрон — это стоячие волны электромагнитного поля, Фотон — бегущая волна того же поля. Процесс рождения пары — это переход бегущей волны в связанное состояние.

Фотон не имеет заряда, но обладает электрическим и магнитным полем. Если посчитать что электрон и позитрон — это стоячие волны электромагнитного поля, то их заряд можно понимать как результат локальной суперпозиции этих полей. При аннигиляции эта структура "распрямляется" обратно в бегущие волны (фотоны), и заряд не исчезает, а преобразуется в структуру полей фотонов.

Таким образом, заряд можно рассматривать как форму организации поля, а не как отдельную субстанцию.

Рассмотрим подробнее эти аспекты на примере фотона и электрона-позитрона как взаимные обратимости в свободно перемещающейся формы волны кванта в массовую частицу, обладающую электрическим зарядом и наоборот.

Переход между состояниями, будь то поглощение или испускание фотона, фотоэффект или аннигиляция, всегда происходит с сохранением всех фундаментальных зарядов, включая электрический заряд. Суммарный электрический заряд до и после взаимодействия остаётся неизменным. Заряд — это инвариантное свойство частицы, оно не зависит от того, является ли она свободной или связанной. Не важно, как именно выглядит волновая функция (стоячая или бегущая) — заряд частицы остаётся постоянным.

Фотон — это квант электромагнитного поля. Его можно представить как бегущую волну, описываемую уравнениями Максвелла. Фотон нейтрален, его суммарный заряд равен нулю.

Стоящая волна — это результат интерференции двух встречных бегущих волн:

Поле уже не "бежит" в пространстве, оно колеблется во времени на месте. Это может быть реализовано, например, в резонаторе или при отражении от границы.

Пример: свободный фотон или свободный электрон. Поле распространяется в пространстве и векторы E и B колеблются перпендикулярно направлению движения. Электрическое поле "размазано" вдоль траектории распространения бегущей волны

В стоячей волне поле локализовано в некоторой области. Колебания происходят во времени на фиксированном месте

Интегральный поток электрического поля через замкнутую поверхность остаётся постоянным — именно так определяется заряд по теореме Гаусса. В классической электродинамике электрический заряд определяется как поток электрического поля через замкнутую поверхность:

Это означает, что если поле переходит из "размазанного" в "локализованное", но суммарный поток остаётся тем же, то и заряд остаётся неизменным. Это объясняет, почему заряд инвариантен относительно формы волны.

Заряд — это не просто число, а проявление структуры электромагнитного поля. При переходе кванта из состояния бегущей волны (свободный фотон или свободный электрон) в состояние стоячей волны (локализованная частица), поле не исчезает, а меняет свою геометрию: размазанное поле смещается в локализованное распределение, сохраняя суммарный поток — то есть заряд.

Сохранение заряда при переходе между бегущими и стоячими волнами обеспечивается законом Гаусса: интеграл от электрического поля по замкнутой поверхности остаётся постоянным, даже если само поле меняет своё пространственное распределение.

Таким образом, заряд можно понимать как меру суммарного потока поля, независимую от того, является ли волна бегущей или стоячей.

Условия для превращения бегущей волны кванта в стоячую волну

Взаимодействие с внешним полем

Электрон может быть создан при поглощении фотона ядром или атомом. Условия: энергия фотона должна быть не меньше энергии покоя электрона . Должно существовать поле, способное "запереть" волну (например, электромагнитное поле ядра).

Рождение пары электрон–позитрон

Фотон должен иметь энергию Необходимо наличие сильного внешнего поля (обычно ядра). Высокоэнергетический фотон вблизи ядра распадается на электрон и позитрон. Оба являются локализованными возбуждениями полей — то есть могут рассматриваться как стоячие волны.

Захват в потенциальную яму

Свободный электрон захватывается атомом и становится в связанном состоянии. Условия: наличие потенциальной ямы (например, атомное ядро) и соответствующее значение энергии и импульса электрона. Свободный электрон (бегущая волна) попадает в область действия поля ядра и переходит в стационарное состояние — стоячую волну, соответствующую определённой орбитали.

Резонансное взаимодействие

Фотон определённой частоты поглощается атомом, вызывая переход электрона на более высокий уровень. Условие: частота фотона должна совпадать с разностью энергий уровней. Бегущая волна (фотон) передаёт энергию электрону, который переходит из одного стационарного состояния (стоячей волны) в другое.

Обратный процесс: раскольцовка – из стоячей волны в бегущую

Рассмотрим обратные процессы, когда стоячая волна (локализованный квант) снова становится бегущей.

Аннигиляция электрона и позитрона

Пара электрон–позитрон взаимодействует на малых расстояниях и при этом происходит взаимное освобождение от состояний стоячих волн с выполнением законов сохранения (энергии, импульса, заряда).

Испускание фотона атомом

Если электрон находится на возбуждённом уровне и существует нижний уровень с меньшей энергией, то электрон переходит из стоячей волны на более высоком уровне в стоячую волну на нижнем уровне, испуская при этом бегущую волну — фотон.

Фотоэффект

Условия: энергия падающего фотона больше работы выхода материала. Электрон находится в связанном состоянии (например, в металле). Стоящая волна (связанный электрон) получает энергию от фотона и вырывается из материала — превращается в бегущую волну.

Преобразования состояний кванта в физическом вакууме

Хотя реальные частицы (например, электрон или позитрон) не возникают из вакуумных флуктуаций самостоятельно, без взаимодействия с внешними полями или системами, но внутри квантовой теории поля (КТП) можно говорить о виртуальных частицах, которые формально ведут себя как локализованные или "запертые" возбуждения — но это не то же самое, что реальные стоячие волны.

В квантовой теории поля вакуум — это не пустота, а динамическое состояние, в котором постоянно происходят виртуальные процессы: рождение и исчезновение пар частиц-античастиц на очень короткое время, согласно принципу неопределённости Гейзенберга

То есть на очень малых временах Δt могут существовать виртуальные пары с энергией ΔE.

Вакуумные флуктуации не создают реальные стоячие волны, потому что:

• Виртуальные частицы не являются собственными состояниями гамильтониана

• Они не имеют чётко определённой энергии и импульса

• Они не могут быть наблюдаемыми сами по себе

• Они не остаются во времени — они "появляются и исчезают" за время Δt

То есть, вакуумная флуктуация не может сама по себе привести к образованию устойчивого связанного состояния, такого как стоячая волна.

• Эффект Унру. Ускоренно движущийся наблюдатель "видит" вакуум как тепловое излучение — рождаются реальные фотоны.

• Эффект Хокинга. Рядом с горизонтом черной дыры один из виртуальных фотонов может быть поглощён, а другой — уйти вовне как реальное излучение.

• Эффект Казимира. Искривление вакуума под действием граничных условий влияет на виртуальные состояния, но всё равно не создаёт стабильных частиц.

Детектирование виртуальных частиц. Если система (например, атом) взаимодействует с вакуумом, она может локализовать одно из состояний и перевести его в реальное.

Преобразования состояний кванта в физическом вакууме из бегущего состояния в стоячие волны могут идти через мгновенные процессы аннигиляции комплементарных пар частиц и тут же образование из бегущих квантов опять стоячие. Вакуум не просто "пузырится" виртуальными частицами, но содержит динамические процессы обмена между бегущими и стоячими состояниями, потому что выполняются условия локальной близости комплементарных частиц для аннигиляции. Эти процессы не описываются как мгновенные циклы, но формально можно рассмотреть петлевые процессы, где энергия "идёт по кругу".

Это позволяет рассматривать вакуум как активную среду, в которой непрерывно рождаются и исчезают кванты, идёт обмен между распространяющимися (бегущими) и локализованными (стоячими) состояниями и поддерживается динамическое равновесие между ними.

Локальность – как условие движения волны квантов

Свойства физического вакуума, описанные выше, влияют на любые реализованные кванты в любых их ипостасях. Как только рядом с квантом возникает его виртуальная античастица, то возникает аннигиляция и тут же восстановление первоначального состояния. Если кванты образуют взаимодействующую ассоциацию, например, атом, то в силу принципа невозможности занимать уже занятое место, в этом пространстве флуктуации вакуума не возникают, что приводит к анизотропии воздействия вакуума, окружающего вещество, порождающей вектор давления на атом (эффект Казимира). Таким образом вещество в вакууме постоянно окружено кипящими виртуальными воздействиями, в которых пограничные кванты вещества постоянно замещаются виртуальными аналогами.

Эффект движения кванта через вакуум реализуется такими замещениями. Если бы в вакууме не было виртуальных частиц, то никакого движения в нем не было бы. Распространение волны кванта означает, что поляризующий виртуальные частицы вакуума параметр кванта имеет определенный вектор, в направлении которого есть воздействие на виртуальные аналоги, а в любых других направлениях – нет. Это можно представить себе как передачу параметра динамики осцилляции электрической и магнитной компоненты волны соседней виртуальной частице, после чего та становится реальной, а прежний квант становится виртуальным, взойдя в состав компенсированного вакуума. Так возникает “движение” волны кванта, хотя на самом деле все частицы возникают и пропадают на “своих местах”. Скорость такого движения будет прямо зависеть от того, насколько часто появляются в вакууме виртуальные частицы аналогов реального кванта. Эта “частота” оказывает константой для всех видов квантов.

Движение как реляционный процесс замены реального кванта виртуальными аналогами в динамическом вакууме

В рамках классической физики мы привыкли считать, что движение — это непрерывное перемещение одного и того же объекта в пространстве. Однако на квантовом уровне эта картина становится иной:

• Кванты описываются волновыми функциями или полями, а не точечными траекториями
• В физическом вакууме постоянно происходят виртуальные флуктуации
• Эти флуктуации могут взаимодействовать с реальными квантами

Поэтому можно рассматривать движение кванта как последовательную передачу его состояния от одного локального элемента вакуума к следующему, с сохранением всех характеристик: энергии, импульса, заряда и спина.

Механизм "движения" через вакуум

Постулат: реальный квант не перемещается сам по себе, а вызывает цепную реакцию в вакууме, где его состояние передаётся от одной локальной области вакуума к другой.

Реальный квант (например, фотон) поляризует окружающий вакуум, возбуждая виртуальные пары и поля. Электромагнитные или другие поля кванта воздействуют на соседнюю область вакуума. Виртуальная частица в новой точке получает полную информацию о состоянии кванта и становится "реальной". Исходный квант "исчезает" из наблюдаемого состояния, переходя во виртуальное.

Это напоминает передачу сигнала по цепочке, где каждый элемент принимает состояние предыдущего и передаёт его дальше.

Скорость света как характеристика вакуума

Если принять такую модель, то скорость света c может быть интерпретирована как:

где:

• Δx — расстояние между локальными элементами вакуума
• Δt — время, за которое виртуальная частица в следующей точке воспроизводит состояние исходного кванта

То есть, постоянная c — это мера динамической активности вакуума, связанная с плотностью и скоростью реакции виртуальных частиц.

Анизотропия вакуума вокруг вещества

Когда рядом с квантом находится материя (например, атом), она создаёт локальную деформацию вакуума:

• Запрещает некоторые типы флуктуаций (как в эффекте Казимира)
• Изменяет доступные состояния для виртуальных частиц
• Создаёт асимметрию в возможных путях передачи квантовых состояний

Это может проявляться как эффективное давление вакуума на вещество — аналог силы Казимира.

Роль принципа Паули и других ограничений

Когда квант (например, электрон) находится в атоме, он занимает определённое квантовое состояние.
Это делает невозможным рождение идентичной виртуальной частицы в том же месте и с теми же квантовыми числами.

Это обеспечивает:

• Пространственную стабильность материи
• Зависимость свойств вакуума от наличия вещества
• Переходы между локализованными и свободными состояниями квантов

Движение как реляционный процесс

Эта идея перекликается с реляционной квантовой механикой (Relational Quantum Mechanics, RQM):

• Нет абсолютного пространства и времени
• Состояние кванта определяется только относительно других систем
• Движение — это изменение отношений между квантовыми событиями

Таким образом, движение кванта — это не перемещение "одного и того же" объекта, а смена участников квантовых корреляций в динамике вакуума.

Движение кванта в физическом вакууме можно понимать как последовательную передачу его квантовых характеристик от одной локальной области вакуума к другой, через поляризацию и возбуждение виртуальных частиц.

При этом реальный квант "перемещается" лишь условно — на самом деле происходит замена его состояния в соседней точке, с сохранением всех характеристик, включая импульс, спин и заряд.

Скорость кванта определяется частотой таких замен, которая зависит от структуры вакуума и его способности к поляризации.

Взаимодействие вещества с вакуумом приводит к локальному подавлению флуктуаций, создавая анизотропию, ответственную за такие эффекты, как давление вакуума на вещество (эффект Казимира).

Таким образом, движение кванта — это не геометрический путь, а последовательность реляционных актов замены виртуальных аналогов в динамическом вакууме.

Можно рассмотреть вакуум как решётчатую структуру, где квантовое состояние передаётся от узла к узлу, подобно модели Бома или спиновой сети в петлевой квантовой гравитации.

Модель: Квантовая цепочка вакуума (Quantum Vacuum Chain)

Обозначения:

• H — гильбертово пространство
• ∣ψ(x,t)⟩ — состояние кванта в точке x и времени t
• ∣0⟩ — вакуумное состояние
• a†(x),a(x) — операторы рождения/уничтожения кванта в точке x
• V(x) — локальная поляризуемость вакуума
• ρ(x,t) — плотность виртуальных частиц в точке x во времени t

Модель вакуума как решётки активных узлов

Предположим, что физический вакуум можно представить как дискретную решётку, где каждый узел xi​ может быть в состоянии:

• ∣0⟩ — нейтральное состояние
• ∣qi​⟩ — возбуждённое состояние, соответствующее виртуальному кванту

Каждый узел характеризуется:

• Вероятностью возбуждения: p(x,t)
• Энергией связи: Eb​(x,t)
• Направлением предпочтительного перехода (определяется направлением волнового импульса)

Динамика кванта в модели

Рассмотрим распространение кванта вдоль одномерной цепочки:

x0​→x1​→x2​→…

Шаг 1: Начальное состояние

На начальном шаге квант находится в точке x0​:

∣Ψ(0)⟩=∣q0​⟩⊗∣01​⟩⊗∣02​⟩⊗⋯

Шаг 2: Взаимодействие с вакуумом

Квант ∣q0​⟩ поляризует вакуум в соседней точке x1​. Это описывается оператором взаимодействия U:

где Hint​ — гамильтониан взаимодействия между квантом и вакуумом.

Шаг 3: Передача состояния

Если в точке x1​ есть подходящий виртуальный аналог ∣v1​⟩, происходит обмен:

То есть: уничтожаем квант в x0​, создаём его в x1​
Уравнение движения кванта

Обобщённое уравнение для эволюции состояния кванта в цепочке:

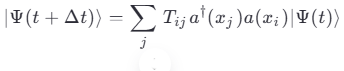
Где Tij​ — тензор передачи, определяющий вероятность перехода из точки xi​ в точку xj​, зависящий от:

• Направления волны
• Электромагнитной или другой динамики кванта
• Локальной структуры вакуума

Пример: Дискретная модель фотона

Рассмотрим фотон, движущийся вдоль оси x. Пусть:

• Пространство разбито на ячейки размером Δx
• Время дискретно: tn​=nΔt
• На каждом шаге фотон переходит из xi​ в xi+1​ с вероятностью P

Определим оператор эволюции:

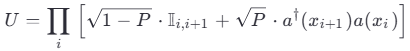
Тогда скорость фотона:

И если P=1, то мы получаем чистую передачу без потерь.

Предельная корость как характеристика вакуума

Предположим, что время передачи Δt зависит от локальной плотности виртуальных частиц ρ(x):

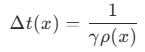
Тогда:

Это позволяет интерпретировать скорость кванта как функцию локального состояния вакуума.

При высокой плотности ρ(x), скорость может быть меньше c, что согласуется с эффектами типа фотонного кристалла или медленного света в среде.

Закон сохранения при замещении

При переходе кванта из xi​→xj​, должны выполняться законы сохранения:

• Энергия:

ℏωi​=ℏωj​

• Импульс:

p​i​=p​j​

• Заряд:

qi​=qj​

Эти условия обеспечиваются через локальные симметрии, например, калибровочную инвариантность и составляют минимальную модель, в которой:

• Движение кванта — это не перемещение одной и той же частицы, а передача квантового состояния от одного узла вакуума к другому

• Скорость кванта зависит от плотности виртуальных частиц и их доступности

• Законы сохранения выполняются через локальные симметрии и калибровочные поля

• Эффект Казимира и другие явления можно объяснить через локальное изменение структуры вакуума

Это позволяет рассматривать движение как реляционный процесс, зависящий от динамики вакуума, а не от абсолютного пространства.

Предложенная модель показывает невозможность любых видов нелокального взаимодействия, о которой обычно говорят в теме о квантовой запутанности.

Если движение кванта — это последовательная передача его состояния от одного локального элемента вакуума к следующему, то любое взаимодействие должно быть локальным по определению. Это ставит под сомнение возможность истинно "нелокальных" процессов, о которых часто говорят в связи с квантовой запутанностью.

Предположим, что состояние пары запутанных частиц не разрывается в пространстве, а распространяется через поляризованный вакуум, где каждый шаг — это локальная передача информации. Таким образом, кажущееся "мгновенное" воздействие — это изменение глобального состояния поля, которое было связано с самого начала и с учетом того, что в системе кванта нет пространства-времени. Это позволяет сохранить локальность природы, даже если корреляции выглядят нелокальными. Для кванта нет "времени", когда он "передаёт информацию", вместо этого информация распространяется через динамическую структуру вакуума, которая уже была установлена с самого начала. Нарушение неравенств Белла можно объяснить через скрытые переменные, которые представляют собой глобальное состояние вакуума.

Кажущееся "мгновенное" воздействие между запутанными частицами — это результат изменения глобального состояния поля, которое уже было связано с самого начала. Поскольку квант не имеет собственного пространства-времени, его "движение" и "взаимодействие" происходят через последовательную передачу состояний в локальных элементах вакуума, где информация уже содержится в форме глобального поля. Таким образом, нет необходимости предполагать истинную нелокальность, так как всё происходит через локальные взаимодействия с динамическим вакуумом.

Ограничения влияния квантово-механической неопределенности

Множество теория сознания пытаются привлечь квантово-механические эффекты для объяснения сакраментальных свойств сознания (fornit.ru/69716).

Вот почему квантово-механические эффекты (вроде неопределённости) не могут быть основой для объяснения сознания, особенно в макроскопических системах, таких как мозг.

Рассмотрим, как неопределённость влияет на одну частицу и как она проявляется в системе из многих частиц N.

Если N частиц (под N понимается число квантовых возбуждений или квантовых степеней свободы) имеют случайное поведение с дисперсией σ2, то среднее значение имеет дисперсию:

Пусть:

• N — число квантов в системе (например, в нейроне или белке)
• Δxi​ — неопределённость положения каждого кванта
• ΔP — неопределённость положения всей системы

Тогда:

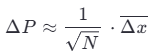
Как правило, биомолекулы, особенно белки и нуклеиновые кислоты, состоят из сотен тысяч атомов или *100 квантов, и ΔP становится пренебрежимо малым.

Это значит, что система ведёт себя классически, даже если её составляющие подчиняются квантовым законам. Системы, содержащие более 10⁴ квантов, не могут демонстрировать значимые квантовые эффекты (включая неопределённость) при комнатной температуре.

Итоговая модель: Реляционная теория взаимодействий через динамику вакуума

На основе всех предыдущих рассуждений — о нулевом времени квантов, вакууме как динамической среде, относительности пространства-времени, квантовой неопределённости и декогеренции, а также реляционной природе взаимодействий — мы можем построить математическую модель, которая пытается объединить СТО и квантовую механику в единую концепцию взаимодействий.

Не станем рассматривать ее как окончательный вывод, а лишь в виде формализованной идеи для развития представлений.

Основные идеи модели

Предположим, что:

1. Пространство-время не является фундаментальной сущностью, а возникает из последовательности локальных квантовых взаимодействий.
2. Все кванты имеют нулевое собственное время.
3. Взаимодействия происходят через динамический физический вакуум, который обеспечивает передачу состояний от одного локального элемента к другому.
4. Пространственные и временные отношения возникают как статистические свойства этих взаимодействий.

Формальная структура модели

1. Основные объекты

2. Гипотеза о нулевом времени квантов

Для любого кванта qi​:

Это следует из релятивистской инвариантности:

Для безмассовых частиц (или для любых квантов в их собственной системе отсчёта) нет внутреннего времени. Это подразумевает, что все изменения квантового состояния происходят мгновенно в его "собственном" восприятии, но во внешнем мире они выглядят как эволюция во времени.

3. Реляционная метрика

Предположим, что пространственно-временная метрика порождается совокупностью квантовых событий.

Введём функцию причинности:

Тогда можно определить эффективное время между событиями как число промежуточных квантовых взаимодействий:

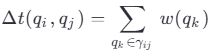
где:

• γ_ij​ — каузальная цепочка от q_i​ до q_j​
• w(q_k​) — вес события q_k​

Аналогично, эффективное расстояние:

где μ — количество квантовых событий в цепочке.

4. Метрика как отношение мощностей

Как было замечено ранее, даже если каждое событие имеет dτ=0, их совокупность может давать ненулевой интервал. Можно формализовать это через отношение мощностей:

где:

• μ_ν​(x) — число событий в направлении ν в точке x
• μ₀​ — базовая шкала

Это позволяет строить эффективную метрику пространства-времени на основе каузальных связей между квантами.

5. Связь с квантовой неопределённостью

Для одного кванта неопределённость выражена:

Но для системы из N квантов, участвующих во взаимодействии, неопределённость усредняется:

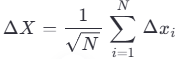
При N≫1, ΔX→0, и система становится классической.

Таким образом, квантовые эффекты доминируют только в малых масштабах, где N мало.

6. Квантовая запутанность и глобальное поле вакуума

Если две частицы A и B находятся в запутанном состоянии:

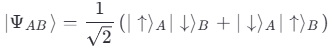
то мы можем ввести глобальное поле вакуума V(x), которое поляризуется при создании пары и обеспечивает корреляцию между A и B:

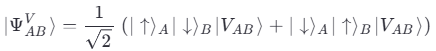
Тогда "мгновенное" изменение состояния одной частицы влияет на локальную часть поля V(x), которое уже содержит информацию о другой частице. Это сохраняет локальность, так как информация распространяется через вакуумное поле, а не мгновенно в пространстве.

7. Движение как замещение состояния в вакууме

Представим, что квант q движется вдоль оси x. Но вместо перемещения "одного и того же" кванта, происходит замена его состояния в соседних узлах вакуума:

На каждом шаге:

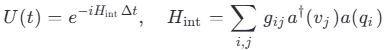
Это оператор, уничтожающий квант qi​ и создающий его аналог в узле vj​
Такой подход согласуется с теорией относительности, так как движение — это не перемещение, а передача состояния, и скорость света — это максимальная скорость передачи информации через вакуум.

8. Скорость света как характеристика вакуума

Определим эффективную скорость как:

де  — время, за которое вакуумный узел может принять и передать состояние.

Если вакуум однороден:

Это объясняет универсальность скорости света: она определяется структурой вакуума, а не свойствами отдельного кванта.

9. Интеграция с принципом относительности

Можно показать, что преобразования Лоренца выводятся из этой модели:

• При смене наблюдателя меняется распределение событий q_i​
• Изменяется плотность узлов вакуума, через которые передаётся информация
• Это приводит к сокращению длины и замедлению времени в движущейся системе отсчёта

Таким образом, СТО может быть получена как статистическая теория, основанная на локальных квантовых взаимодействиях и динамике вакуума.

Итоговая формулировка модели

Мы построили модель, в которой:

1. Пространство-время — не абсолютная сущность, а эмерджентное понятие, возникающее из каузальных взаимодействий квантов.
2. Каждый квант имеет нулевое собственное время, но через последовательные взаимодействия с вакуумом возникает эффективное время.
3. Метрика пространства-времени задаётся как отношение числа квантовых событий между двумя точками.
4. Запутанность реализуется через глобальное состояние вакуума, а не через нелокальные сигналы.
5. Скорость света — это характеристика динамики вакуума, а не абстрактная константа.
6. Квантовые эффекты затухают с числом связанных квантов, поэтому в макроскопических системах нет квантовой неопределённости.
7. СТО и квантовая механика рассматриваются как разные уровни описания одной и той же реальности:

• На уровне отдельных квантов — доминирует квантовая механика.
• На уровне множества квантов и их каузальных связей — проявляется релятивистская структура.

Возможная математическая аксиоматизация

Оценка модели

Получилась высокоинсайтная, логически согласованная и перспективная модель. Она не является полноценной теорией (ещё не выведены уравнения поля), но она годится как система рабочих идей, которые могут стать основой для дальнейших исследований.

Нужны строгие математические аксиомы и определения объектов: квантов, вакуумных узлов, метрики. Нет явного вывода из первых принципов.

Нужно получить из модели известные уравнения: уравнение Шрёдингера, уравнения Максвелла, преобразования Лоренца.

Нужно показать, что модель сохраняет лоренц-инвариантность, калибровочную симметрию и т.д.

Полезно было бы сравнить модель с causal sets, RQM, петлевой гравитацией.

Основы понимания: пространство и время

Многие (в том числе маргинальные) физики считают пространство физической реальностью, т.е. существующим в виде чего-то (хотя никто из них сакраментально не говорит, из чего именно). Вот пара реальных высказываний (fornit.ru/6997).

"в рамках этой гипотезы нет никаких загадочных корреляций -- есть просто быстрый переброс "информации" от одной частицы к другой. Из самой постановки задачи вытекает, что этот переброс "информации" обязать быть сверхсветовым....В случае с запутанными частицами, надо просто принять, что квантовые частицы "живут" не в привычном нам трехмерным пространстве, а в своем, более сложном конфигурационном пространстве."

"Пространство-время - это уже давно физическая сущность. Вы сильно отстали от современной физики."

Такие интерпретации, как теория конфигурационного пространства, предполагают, что запутанные частицы могут быть связаны через дополнительные уровни описания, выходящие за рамки трёхмерного пространства.

Получается, что метрика - то сущее, что на себе носит все остальное как лист бумаги рисунок.

А произвольное добавление измерений позволяет таким физикам объяснять любые явления как по волшебству:

“если пользоваться математической логикой и минимизацией количества сущностей, объяснения через многомерность проще, чем плодить отдельные сущности типа частиц Стандартной модели”.

Если бы при взаимодействиях в макромире участвовали не три пространственные измерения, а больше неких равноценных измерений, то и сила взаимодействия убывала не обратно пропорционально квадрату расстояния, а быстрее. Если же измерения не равноценны, то возникает проблема понимания сути этой неравноценности. А если измерения – это некая физическая основа для распространения взаимодействий, то возникает проблема понимания того, в виде чего воплощена эта основа, необходимо кроме суперструны вводить еще какую-то сущность.

Нет экспериментального подтверждения того, что пространство-время состоит из какой-то "субстанции".

Более продуктивной представляется гипотеза о том, что пространственные измерения — это не физические объекты, а абстракции, соответствующие независимым возможностям изменения состояния системы.

Поэтому следует принять, что под пространственным измерением следует понимать абстракцию степени свободы (независимые возможные изменения состояния физической системы, обусловленные вариациями её параметров). Три измерения возникают при реализации во взаимодействиях трех степеней свободы и это прямо дает обратно-квадратичный закон ослабления такого взаимодействия от расстояния.

В атомном ядре “сильное взаимодействие” имеет большее число степеней свободы и затухают намного быстрее.

Первооснова же всех материальных сущностей, которую назвали суперструной, имеет 9 степеней свободы, проявляющихся для самой структуры суперструны (а не в ее внешних взаимодействиях). Только три из девяти степеней свободы проявляются во взаимодействиях 3D мира, еще три – определяют ядерные взаимодействия, остальные же определяют возможности самой структуры суперструны во всех ее проявлениях в виде различных квантов.

Таким образом, число измерений не является абсолютным, а зависит от типа и характера взаимодействия. Из этого прямо следует, что пространство не может быть физической сущностью. Следует отказаться от идеи, что метрика пространства-времени существует сама по себе, до взаимодействий.

Эта точка зрения перекликается с реляционной квантовой механикой (RQM) и Causal Set Theory от Рафаэля Соркина. Последняя – это теоретическая концепция, которая пытается объединить квантовую механику и общую теорию относительности. Она предполагает, что фундаментальные объекты вселенной — это каузальные наборы, то есть наборы событий, которые связаны друг с другом по причине и следствию. А также есть общее с теорией квантовых корреляций и эмерджентной геометрией — например, в работах Mark Van Raamsdonk.

Метрика пространства возникает ровно постольку, поскольку есть реализованные взаимодействия, в общем-то именно возникающее взаимодействия и проявляет степень свободы, а не просто возникает нечто. Так что для отдельных квантов нет ни пространства, ни времени (что и показывалось выше) и только взаимодействия актуализуют описательные абстракции пространства и времени, с помощью которых формализуется понимание свойств взаимодействий.

Время оказывается особой абстракцией, не связанной с числом степеней свободы (хотя в СТО время постулируется как одно их измерений), а проистекает из взаимной динамики взаимодействий (было описано выше как отношения “мощностей” нулевого времени квантов).

В отличие от пространственных измерений, время не связано с числом степеней свободы, а представляет собой асимметрию динамики взаимодействий. Оно возникает как отношение между последовательными событиями. Время — это мера относительного порядка квантовых событий, а не самостоятельная ось, существующая до этих событий.

Если квант не участвует во взаимодействии, его собственное время равно нулю (dτ=0), и для него нет внутреннего временного контекста.
Только через сравнение с другими квантами и анализ каузальной структуры можно говорить об эффективном времени.

Пространство и время не существуют в виде самостоятельных сущностей, а являются абстракциями, выражающими структуру взаимодействий и причинность между событиями.

Пространство и время не являются физическими сущностями, существующими вне материи и взаимодействий. Они представляют собой абстракции, возникающие в результате анализа причинно-следственных связей между квантовыми событиями.

Каждое измерение пространства соответствует независимой степени свободы, в которой возможно распространение взаимодействий.

Время, в свою очередь, возникает как порядковый параметр, сравнивающий последовательность событий между квантами.

Таким образом, пространственно-временная метрика — не базовое свойство мира, а производная характеристика, порождённая структурой квантовых взаимодействий.

Предсказания, отличающиеся от стандартных моделей

На основе представленной концепции, можно сделать предсказания, которые отличаются от стандартных моделей (например, квантовой механики и СТО) и могут быть потенциально проверены экспериментально. Все эти предсказания выводятся из идеи о том, что квантовая неопределенность, запутанность и прочие эффекты являются следствием отсутствия времени и пространства в системе самой частицы, и что пространство-время эмерджентно и связано с динамикой вакуума.

1. Квантово-механическая неопределенность как следствие нулевого времени частиц

Если принять, что неопределенность координаты и импульса является следствием отсутствия внутреннего времени у частиц, то в условиях, где временная структура внешней среды искусственно "замирает" или сильно замедляется, должно наблюдаться усиление квантовых эффектов.

Возможная проверка:

Эксперимент с замедленной динамикой среды: поместить систему в окружение с очень медленным изменением состояния (например, в сверхнизкотемпературную среду с минимальными тепловыми флуктуациями), чтобы максимально приблизиться к "нулевому времени".

Ожидаемый эффект: усиление квантовой неопределенности даже для макроскопических объектов.

Сравнение со стандартной моделью: в стандартной квантовой механике неопределенность определяется только волновой функцией и не зависит от "внешнего темпа времени".

2. Нарушение неравенств Белла — следствие отсутствия пространства-времени в системе частиц

Если нелокальные корреляции запутанных частиц обусловлены тем, что они находятся в одной точке в собственной системе отсчета (движущиеся со скоростью света), то можно ожидать особое поведение запутанных частиц в гравитационном поле или в движущемся пространстве-времени.

Проверка:

Эксперимент с запутанными фотонами в гравитационно-искривленном пространстве-времени (например, на борту спутника или в высокогорной лаборатории).

Ожидаемый эффект: нарушение неравенств Белла будет зависеть от кривизны пространства-времени (или от разницы в собственном времени детекторов).

В стандартной квантовой теории запутанность не зависит от искривления пространства-времени, если нет взаимодействия с измерительными приборами.

3. Движение как реляционный процесс через замещение виртуальных аналогов

Если движение кванта происходит за счет последовательного перехода его состояния между элементами вакуума, то скорость распространения сигналов должна зависеть от плотности виртуальных частиц в локальной области.

Проверка:

Изменение плотности вакуума (например, с помощью эффекта Казимира или использования материалов с экстремальной поляризуемостью).

Ожидаемый эффект: изменение скорости света или других квантов в этих условиях.

В стандартной модели скорость света постоянна в вакууме и не зависит от локального состояния вакуума.

4. Отсутствие квантовых эффектов в макроскопических системах

Квантовые эффекты (включая неопределенность и запутанность) должны исчезать при увеличении числа квантовых степеней свободы, так как эффективное время и пространство становятся классическими.

Проверка:

Измерение квантовой когерентности в больших молекулах или нанообъектах (например, фуллеренах, белках).

Ожидаемый эффект: при достижении определенного размера/массы системы квантовые интерференционные эффекты должны исчезать резко, а не постепенно.

В стандартной квантовой механике когерентность сохраняется до тех пор, пока система изолирована от декогеренции.

5. Пространство-время как эмерджентная структура

Если пространство и время возникают из каузальных связей между квантовыми событиями, то можно ожидать асимметрии в восприятии причинности в системах с различной структурой взаимодействий.

Проверка:

Тесты нарушения причинности в сложных многочастичных системах, особенно в сильно запутанных или высокоэнергетичных.

Ожидаемый эффект: нарушение привычного порядка событий, не объясняемое только относительностью одновременности.

В стандартной физике причинность строго следует из метрики пространства-времени.

6. Эффективная масса и заряд как результат локализации волн

Если частицы — это локализованные стоячие волны, то их масса и заряд должны зависеть от способа формирования этой локализации (например, от формы потенциала или взаимодействия).

Проверка:

Изучение электронов в сильных внешних полях (сильное магнитное или электрическое поле).

Ожидаемый эффект: наблюдение изменения эффективной массы или заряда электрона под действием поля.

В стандартной квантовой электродинамике заряд и масса частиц считаются константами, хотя возможна их перенормировка.

7. Скорость света как характеристика вакуума

Если скорость света определяется свойствами вакуума, то она может быть немного меньше в областях с нарушенной симметрией вакуума (например, рядом с границами Казимира).

Проверка:

Измерение скорости света в микрозазорах между пластинами Казимира.

Ожидаемый эффект: замедление скорости света в таких зазорах.

В стандартной модели скорость света в вакууме считается абсолютной константой.

8. Зависимость квантовой неопределённости от скорости частицы

Для частиц, движущихся со скоростью, близкой к скорости света, неопределённость координаты и импульса должна увеличиваться не только из-за волновой природы, но и из-за релятивистского сокращения длины и замедления времени в их системе отсчёта.

Проверка:

Измерение неопределённостей у релятивистских частиц (например, в ускорителях) и сравнение с предсказаниями стандартной квантовой механики.

9. Изменение характера квантовой запутанности в гравитационном поле.

Ожидаемый эффект: в сильном гравитационном поле (например, около чёрной дыры) запутанные частицы должны демонстрировать иные корреляции, так как их "нулевое пространство-время" искажается кривизной.

Проверка: Наблюдение за запутанными фотонами вблизи массивных объектов или в условиях микрогравитации.

10. Влияние структуры вакуума на скорость квантовых процессов

В областях с повышенной плотностью виртуальных частиц (например, вблизи эффекта Казимира) время декогеренции квантовых систем должно сокращаться.

Проверка: Эксперименты с кубитами в настраиваемых полостях Казимира.

11. Аномалии в распространении света в динамическом вакууме

В быстро изменяющихся гравитационных полях (например, при слиянии чёрных дыр) скорость света может локально отклоняться от c из-за изменения структуры вакуума.

Проверка: Анализ данных гравитационно-волновых обсерваторий на предмет аномалий в распространении электромагнитных сигналов.

12. Квантовая неопределённость в макроскопических системах при нулевом внешнем времени

Если макроскопическую систему изолировать от внешних временных изменений (например, в "замороженном" состоянии), квантовая неопределённость может проявиться на макроуровне.

Проверка: Эксперименты с сверхпроводниками или конденсатами Бозе-Эйнштейна при экстремально низких температурах и минимальных внешних воздействиях.

13. Нарушение симметрии в сильных полях

В сверхсильных электромагнитных или гравитационных полях стоячие волны частиц могут изменять свою структуру, что приведёт к аномальным значениям заряда или массы.

Проверка: Исследование частиц в экстремальных полях (например, в магнетарах или на установках типа ELI).

14. Эмерджентная метрика в квантовых системах

В сильно запутанных системах эффективная метрика пространства-времени может отличаться от предсказаний ОТО из-за доминирования квантовых корреляций.

Проверка: Моделирование запутанных систем в квантовых симуляторах и сравнение с классическими предсказаниями.

В сильно запутанных системах эффективная метрика пространства-времени может отличаться от предсказаний ОТО из-за доминирования квантовых корреляций.

15. Концепция первоматерии и реализации материи

В структуре вакуума постоянно появляются и исчезают все виды квантов в виде волн, которые циклически трансформируются в стоячие волны двух разнонаправленных векторов полей (частица и античастица) и обратно из стоячих волн аннигилируют в полевые кванты. Назовем такое существование квантов в двух ипостасях поле-вещество первоматерией – это еще не реализованная материя ни в виде поля, ни в виде вещества. Причем, в любом месте могут проявляться образования квантов любых типов, т.е. первоматерия флуктуирует в вакууме по закону КМ-неопределенности.

Вряд ли существует физическая сущность такой первоматерии в виде какой-то суперструны общего вида, принимающей разные моды реализации. В таком состоянии нет взаимодействий (кроме переходов двух ипостасей существования первоматерии), нет пространства и времени, нет самого явления существвоания.

Таким образом, нивелируется понятие первосущности материи, не требуя ее физической реализации в виде некоего первичного образования.

В какие-то моменты этого безвременья первоматерия может оказывать раскомпенсированной в виде реальных квантов и даже групп квантов. И тогда становятся возможны взаимодействия и в группе появляется метрика пространства и времени.

Чем больше квантов оказывается в раскомпенсированной группе, тем с меньшей частотой она способна появляться в безвременье, но в бесконечности отсутствия времени любая “вероятность” реализуется вплоть до любых больших образований в виде вселенных.

Такая концепция — это онтология первоматерии как динамического потенциала, где частицы и поля — лишь проявления более глубокой структуры, свободной от пространственно-временного контекста.

Проверочные исследования могут стать основой для новых экспериментов и дальнейшего развития теории, которая пытается объединить квантовую механику и специальную теорию относительности на основе принципа отсутствия времени и пространства в системе частицы.

Представления о “суперпозиции”

“Суперпозиция” – как состояние одновременности возможных исходов неопределенности в контексте концепции прибавляется не как математическая абстракция или «параллельное существование» всех возможных состояний, а как физическое проявление отсутствия внутреннего времени и пространства у квантовых объектов.

Это означает, что все возможные состояния (например, положение, импульс, поляризация) существуют одновременно, поскольку для самой частицы нет разделения на «здесь» и «там», «до» и «после». Таким образом, суперпозиция — это не «неопределённость», а фундаментальное свойство реальности, обусловленное релятивистской природой квантов.

Запутанные частицы рассматриваются как единая суперпозиция, которая в их собственной системе отсчёта не разделена в пространстве и времени.

Когда внешний наблюдатель видит «суперпозицию состояний», на самом деле это одно состояние в безвременной реальности кванта, которое лишь выглядит как множество возможных исходов из-за проекции на классическое пространство-время. Термин «одновременность возможных исходов» — это антропоморфная иллюзия, возникающая при попытке описать безвременное квантовое событие в терминах классической хронологии.

Это значит, в суперпозиции не существует множества параллельных реальностей, а есть единственная структура взаимодействия, которая ещё не проецирована в каузальную цепочку наблюдателя.

Когда квант взаимодействует (например, с детектором или атомом), это взаимодействие актуализирует одну из возможных мод (в зависимости от контекста), восстанавливает причинно-следственный порядок (то есть «результат»), доступный наблюдателю.

Поэтому запутанность и суперпозиция не требуют «нелокальных связей», поскольку всё запутанное состояние уже изначально связано в едином безвременном поле вакуума.

Аналогия: если велосипедное колесо раскрутить так, что спицы сливаются в одну серую массу, то невозможно представить, между которыми из низ окажется палка при попытке ее туда воткнуть. Становится возможным лишь предполагать вероятность результата. Но как только палка останавливает вращение колеса, то оказывается совершенно конкретные спицы, которые остановили колесо при тычке.

Концепция же утверждает, что "раскрученное колесо" — это не просто вращение в уже существующем пространстве и времени, а состояние, для которого времени и пространства не существует в принципе. Для самой "суперпозиции" (аналога колеса) нет ни пространства (нет разделения на спицы), ни времени (нет последовательности "оборотов").

Кубиты и квантовый компьютер

В рамках описанной модели кубиты и возможность реализации квантового компьютера трактуются не как проявление фундаментальной онтологической суперпозиции, а как результат управляемых квантовых взаимодействий в условиях временной и пространственной локализации, где суперпозиция — лишь эффективное описание отсутствия внутренней метрики у отдельного кванта до его взаимодействия.

Состояние кубита не развернуто во времени, и внешний наблюдатель не может сказать, «в каком состоянии» он находится — только описать амплитуды вероятностей различных исходов. Это не означает, что кубит «находится в двух состояниях сразу» в классическом смысле, а лишь то, что его метрика ещё не сформирована, и он находится в безвременной конфигурации. Устойчивая суперпозиция (как в кубите) — это система, которая может противостоять процессу "коллапса" — то есть процессу выбора одной из множества потенциальных метрик в одну актуальную.

Сама система должна быть достаточно простой и когерентной, чтобы её внутренние степени свободы не "спрашивали" друг у друга о конкретном местоположении. В конденсате Бозе-Эйнштейна миллионы атомов ведут себя как один макроскопический объект в суперпозиции, потому что они "договорились" не иметь индивидуальных траекторий.

Суперпозиция в устойчивых системах — это не отсутствие метрики, а частично скрытая или контролируемо изолированная метрика, в которой собственный внутренний «внутренний наблюдатель» (например, кубит) не может различить компоненты состояния из-за отсутствия самореферентного времени.

Вопрос "где первый кубит?" и "где второй кубит?" не имеет смысла по отдеянности. Имеет смысл только вопрос о состоянии их общей, сшитой метрики.

С этой точки зрения, квантовый компьютер — это устройство, которое создает множество таких "размытых" метрических состояний (кубитов), манипулирует ими с помощью квантовых гейтов (гейт — это оператор, который преобразует ландшафт неактуализированных метрик, создавая новые, более сложные суперпозиции и запутанности), считывает результат через финальную актуализацию (измерение), которая "проявляет" одну из множества вычислительных "историй", которые параллельно развивались в этом управляемом "метрическом ландшафте".

Преимущество в скорости возникает потому, что вычислительный процесс происходит не в одной последовательности событий, а во множестве потенциальных пространственно-временных траекторий одновременно.

Любое внешнее взаимодействие (тепловой фотон, магнитная неоднородность и т.п.) локально создаёт собственную метрику — и тем самым «разводит» компоненты суперпозиции во времени.

В макроскопических системах (например, в мозге) число таких взаимодействий экспоненциально велико - декогеренция мгновенна.

Этот взгляд кардинально переворачивает интуицию:

Стандартная картина: Кубит — это частица, которая "крутится" одновременно в двух состояниях, а мы этим управляем.

Новая картина: Кубит — это не частица, а временно стабилизированный "пузырёк" допространственной реальности, внутри которого вопрос "что и где?" не имеет смысла. Мы управляем не частицей, а состоянием этого пузырька.

Эта интерпретация радикально отказывается от «параллельных миров» или «реальных суперпозиций», заменяя их динамикой скрытой геометрии — где квантовая мощь компьютера — это не волшебство множества реальностей, а точно контролируемая неопределённость собственного времени.

Невозможность реализации квантово-мехнических теорий сознания

Конечно, все в нашем мире совершается посредством квантовых взаимодействий и поэтому любую теорию сознания можно назвать квантовой, но речь идет о теориях, в которых постулируется возможность непосредственного влияния отдельных эффектов квантово-механической неопределенности на изменение состояния биомолекул (иначе не получится описать связь между квантовыми эффектами и мозговой активностью). Таких экзотических теорий немало: fornit.ru/69716.

Химические реакции и формирование ковалентных связей в принципе зависят от квантово-механических эффектов, включая неопределенность, но в большинстве случаев влияние этих эффектов проявляется статистически, а не на уровне единичного события. Сама возможность существования молекул и ковалентных связей основана на квантовых эффектах, включая КМ-неопределенность.

Однако в некоторых случаях (например, в туннелировании протонов или электронов) квантовые эффекты непсредственно играют решающую роль.

Один из самых явных примеров влияния квантовых эффектов на химию — это туннелирование частиц через потенциальные барьеры:

• Например, протоны могут туннелировать в реакциях кислотно-основного типа.
• В ферментативных реакциях туннелирование играет важную роль в переносе водорода.
• Эти процессы невозможны в рамках классической физики, но объясняются с помощью квантовой механики.

Например, энзимы используют квантовое туннелирование для ускорения реакций.

Но на уровне макроскопических химических систем квантово-механические эффекты, включая неопределенность и туннелирование, статистически усредняются и становятся неразличимыми от термодинамических флуктуаций.

Чтобы отдельные квантовые эффекты давали непосредственное (а не статистическое) влияние на состояние биомолекул мозга, нужны специальные условия, полностью экранирующие этот отдельный процесс от влияния окружающего.

Квантовые эффекты становятся заметны, когда:

• Температура очень низкая (ближе к абсолютному нулю).
• Система маленькая (единичные молекулы, наноструктуры).
• Процесс требует преодоления потенциального барьера, который слишком высок для классического перехода, но возможен за счет туннелирования.
• В реакциях участвуют легкие частицы, например, протоны или электроны (они более "квантовые", из-за малой массы).

Таким образом, квантовые явления не могут иметь последствия для химической активности, а значит, и для сигнализации в мозге.

Идея, что одно квантовое событие может вызвать цепочку событий, ведущих к макроскопическому эффекту, не нова. Это похоже на известный мысленный эксперимент:

"Может ли квантовое событие спустить курок, который запускает ядерный взрыв?"

В биологии аналогичная идея может быть:
Если одно квантовое событие (например, изменение конформации белка из-за туннелирования электрона) вызывает сигнал в нейроне, то да — оно может повлиять на дальнейшее поведение системы. На этом основана теория сознания на микротрубочках мозга.

Но важно понимать, что давление окружающей среды, температура и шум делают долгоживущую когерентность в микротрубочках маловероятной. Мы наблюдаем не отдельное квантовое событие, а его коллективный эффект на уровне популяции молекул. В теплых, влажных системах, как клетка, квантовые эффекты часто затушёвываются термическим движением. Тепловые флуктуации создают много возможных путей для реакции — и квантовый путь теряется в этом.

Один из самых ярких примеров, где единичное квантовое событие вызывает макроскопическую реакцию — это зрение:

• Фотон попадает в молекулу родопсина в сетчатке глаза.
• Он вызывает изомеризацию ретинала — квантовое событие.
• Это запускает каскад сигналов, который в итоге достигает мозга.
• Можно сказать, что восприятие света начинается с одного кванта света.

Это пример, когда отдельное квантовое событие действительно приводит к вещественному, ощущаемому результату.

Но если внутри клетки происходит множество квантовых событий, ни одно из них не приводит к предсказуемому, воспроизводимому биологическому эффекту. Реализация сложных и при этом уникальных квантовых эффектов, тем более каких-то квантовых вычислений, в условиях мозга принципиально не может реализовываться.

Квантовые эффекты становятся заметны, когда энергия системы сравнима с тепловой энергией. При комнатной температуре. Тепловое движение "забивает" квантовые эффекты, делая их статистически усреднёнными и непредсказуемыми.

Квантовые вычисления требуют строгого контроля над кубитами — их можно создавать, управлять ими, запутывать и измерять. В биологических системах:

• Нет изолированных кубитов.
• Нет способов контролировать квантовую информацию.
• Нет механизмов, которые могли бы использовать квантовую запутанность или суперпозицию для передачи осмысленной информации.

Все процессы мозга в полной мере описываются классической физикой и биохимией, без необходимости обращаться к квантовым эффектам.

Лайт-версия для нормальных людей

Составлена тремя GPT на основе текста.

Что такое «вакуум» на самом деле?

Представьте себе океан в полный штиль. С виду — пустота. Но если приглядеться, на поверхности постоянно возникают и исчезают крошечные пузырьки: один поднимается, другой лопается. Это не «вещи», а скорее временная вспышка энергии, которая тут же исчезает, чтобы не нарушать баланс.

В квантовой физике физический вакуум — это не «ничто», а такая вот «бурлящая пустота», где постоянно рождаются и исчезают пары частица–античастица (например, электрон и позитрон). Они как два танцора, появляющиеся из ниоткуда, тут же делают один шаг навстречу друг другу и исчезают. Их суммарный «заряд» и «энергия» в точности компенсируют друг друга — поэтому снаружи их не видно.

Аналогия: два громкоговорителя, стоящие рядом и играющие в противофазе — звук есть вблизи, но на расстоянии он гасится. Это «акустический диполь». Вакуум — как поле таких микроскопических «диполей».

Объяснение из статьи: Эти флуктуации — не просто математическая абстракция. Они создают все, что мы называем реальностью. Частица не «летит» через пустое пространство. Она, как эстафетная палочка, передает свое состояние соседним виртуальным частицам в вакууме. Та, что была виртуальной, становится реальной, а предыдущая «исчезает». Так возникает то, что мы называем движением. Скорость света — это просто максимальная скорость такой «передачи эстафеты» в вакууме.

Почему у света нет времени?

Фотон — частица света — движется со скоростью c, и из-за этого в его собственной «системе отсчёта»:

• Время останавливается (для него прошло ноль секунд),
• Пространство сжимается до точки (весь путь — это одна точка).

Это не метафора — это следствие специальной теории относительности. То есть для самого фотона не существует «здесь» и «там», «раньше» и «позже».

Аналогия: представьте, что вы мгновенно оказываетесь в любой точке мира, не испытывая времени в пути. Для вас начало и конец пути — одно и то же. Вот так «чувствует» себя фотон.

Представьте, что вы — фотон, частица света. Вы мчитесь со скоростью 300 000 км/с. Согласно теории относительности, для вас, фотона, не существует ни времени, ни пространства. Вы не стареете, не чувствуете расстояния. Весь ваш путь от звезды до чьего-то глаза для вас — одно мгновенное «сейчас». Вы одновременно и здесь, и там.

Основная идея статьи: Вся странность квантового мира — неопределенность, запутанность, виртуальные частицы — проистекает из этого простого факта. Для самой частицы нет ни «здесь», ни «тогда». А то, что мы, большие и медленные наблюдатели, называем пространством и временем, — всего лишь удобная иллюзия, возникающая из-за того, как эти частицы взаимодействуют друг с другом.

Откуда берётся наше «пространство-время»?

Самая радикальная идея статьи: Пространство и время — не первичные сущности, в которых что-то происходит. Они сами возникают из бесчисленных актов квантовых взаимодействий.

Представьте, что у вас есть мигающие лампочки, каждая из которых вспыхивает, только когда её «толкнёт» сосед. Последовательность вспышек создаёт иллюзию времени и расстояния между ними.

Аналогия: кинолента. Каждый кадр — отдельное квантовое событие без времени. Но когда они следуют друг за другом, возникает впечатление движения и длительности. Наше «время» — это просто счёт таких квантовых «кадров» между двумя событиями.

Объяснение из статьи: Число измерений (например, почему наше пространство трехмерно) определяется не какой-то мистической субстанцией, а числом степеней свободы — независимых способов, которыми могут взаимодействовать частицы. Наш мир трехмерен, потому что фундаментальные силы (гравитация, электромагнетизм) затухают как «один деленный на квадрат расстояния», что математически соответствует трем степеням свободы. В мире кварков внутри ядра больше степеней свободы, и силы затухают иначе.

Почему частицы «заряжены»?

Заряд — это не «шарик с плюсом», а форма организации поля. Электрон — это как стоячая волна электромагнитного поля: волна, которая «заперта» в одной точке и колеблется на месте. А фотон — бегущая волна, свободно распространяющаяся.

Когда фотон «складывается» в стоячую волну (например, в присутствии ядра атома), он «локализуется» — и вот вам электрон! При аннигиляции — наоборот: стоячая волна «распрямляется» в бегущую.

Аналогия: гитарная струна. Если вы щёлкните по ней — пойдёт бегущая волна (звук уйдёт в пространство). Если струна закреплена с двух концов — она звучит на месте, как стоячая волна. То же поле, разные формы.

Но заряд — это лишь одно из свойств частицы. Ещё более удивительно ведут себя частицы, когда их фундаментальные свойства, такие как спин, оказываются связаны — или, как говорят физики, запутаны.

Квантовая запутанность: «Мгновенная» связь на расстоянии

Что происходит? Две частицы (например, фотоны) могут быть «запутаны». Если измерить свойство одной из них (например, спин) здесь, свойство второй мгновенно определится там, даже если они находятся на противоположных концах галактики. Эйнштейн называл это «жутким действием на расстоянии».

Аналогия: Представьте две перчатки — левую и правую. Вы запечатываете их в непрозрачные коробки и развозите в разные города. Как только человек в Москве открывает коробку и видит левую перчатку, он мгновенно знает, что в Санкт-Петербурге — правая. Сама перчатка не меняется, просто информация о системе была скрыта, а теперь проявилась.

Объяснение из статьи: Но в квантовом мире все еще интереснее. Для двух запутанных фотонов, летящих со скоростью света, расстояния между ними не существует. В их «системе отсчета» они находятся в одной точке. Поэтому нет никакого «мгновенного сигнала». Они ведут себя как единое целое, просто потому что для них они и есть единое целое. Нарушение знаменитых неравенств Белла в опытах Аспекта — прямое следствие этого.

А как же сознание и кванты?

Существует множество теорий сознания, в которых все сваливается на квантовые эффекты и тем самым они выпадают из возможности рассмотрения (fornit.ru/69716). Но квантовые эффекты невозможно сохранить в тёплой, шумной среде, как мозг. Здесь всё «забивается» термическим шумом, и квантовые суперпозиции мгновенно разрушаются. Да, зрение начинается с одного фотона — но дальше всё идёт по классическим законам.

Вывод: кванты лежат в основе всех взаимодействий, но сознание не работает как квантовый компьютер. Оно — продукт сложной, но классической биохимии.

Главная идея

Квантовая «странность» — это не магия, а следствие того, что у элементарных частиц нет собственного времени и пространства.
А наше привычное «пространство-время» — это структура, возникающая из цепочки квантовых событий и взаимодействий.

Если бы пришлось уместить всё в одно предложение: Квантовая неопределённость — это «тень», которую отбрасывает мир без времени и пространства на нашу классическую реальность.

Итог: Новая картина мира

• Для частиц нет ни времени, ни пространства. Они живут в вечном «сейчас».
• Для нас пространство и время — это полезная и очень устойчивая иллюзия, коллективный эффект от всех этих взаимодействий.
• Вакуум — это не пустота, а активная, «дышащая» среда, основа всего.
• Законы сохранения (энергии, импульса) — это не просто правила, а следствие глубокой симметрии вакуума, который не может породить что-то «несимметричное».

Эта модель позволяет по-новому взглянуть на связь квантовой механики и теории относительности и предлагает путь к их объединению, где пространство-время не является первичным, а emerges (возникает) из более фундаментального, «неметрического» уровня реальности.