Диссипативные системы
Диссипативные системы
Диссипативные
системы
Диссипативные
системы (И.Пригожин)
Диссипативные
структуры (В.И.Коротков)
Диссипативная структура, характеризуется нарушением симметрии, множественными выборами и корреляциями в макроскопических масштабах.
Диссипативные системы (www.chat.ru/~cuirt/synergetics.htm)
При изучении систем, их часто описывают системой дифференциальных уравнений. Представление решения этих уравнений как движения некоторой точки в пространстве с размерностью, равной числу переменных называют фазовыми траекториями системы. Поведение фазовой траектории в смысле устойчивости показывает, что существует несколько основных его типов, когда все решения системы в конечном счете сосредотачиваются на некотором подмножестве. Такое подмножество называется аттрактором. Аттрактор имеет область притяжения, множество начальных точек, таких, что при увеличении времени все фазовые траектории, начавшиеся в них стремятся именно к этому аттрактору.
Основными типами аттракторов являются:
- устойчивые предельные точки
- устойчивые циклы (траектория стремится к некоторой замкнутой кривой)
- торы (к поверхности которых приближается траектория)
Уравнения, обладающие странными аттракторами вовсе не являются экзотическими. В качестве примера такой системы можно назвать систему Лоренца, полученную из уравнений гидродинамики в задаче о термоконвекции подогреваемого снизу слоя жидкости.
Замечательным является строение странных аттракторов. Их уникальным свойством является скейлинговая структура или масштабная самоповторяемость. Это означает, что увеличивая участок аттрактора, содержащий бесконечное количество кривых, можно убедиться в его подобии крупномасштабному представлению части аттрактора. Для объектов, обладающих способностью бесконечно повторять собственную структуру на микроуровне существует специальное название — .
Для динамических систем, зависящих от некоторого параметра, характерно, как правило, плавное изменение характера поведения при изменении параметра. Однако для параметра может иметься некоторое критическое (бифуркационное) значение, при переходе через которое аттрактор претерпевает качественную перестройку и, соответственно, резко меняется динамика системы, например, теряется устойчивость. Потеря устойчивости происходит, как правило, переходом от точки устойчивости к устойчивому циклу (мягкая потеря устойчивости), выход траектории с устойчивого положения (жесткая потеря устойчивости), рождение циклов с удвоенным периодом. При дальнейшем изменении параметра возможно возникновение торов и далее странных аттракторов, то есть хаотических процессов.
Здесь надо оговорить, что в специальном смысле этого слова хаос означает нерегулярное движение, описываемое детерминистическими уравнениями. Нерегулярное движение подразумевает невозможность его описания суммой гармонических движений.
Важная роль трения, представляющего собой особую форму диссипативного процесса, была осознана задолго до создания классической механики. Когда Аристотель высказал предположение, что все подлунные динамические системы в общем случае стремятся к равновесию, на самом деле он выражал идею о том, что нечто вроде "трения" должно замедлять движение. В этом плане классический принцип инерции, отражающий основную роль ускорения, а не скорости, соответствует некоторой идеализации, возникающей в результате пренебрежения трением.
Начиная с работ Фурье и Клаузиуса, в XIX в. возрос интерес к диссипативным системам, приводящим к необратимым процессам. Это было довольно естественно с учетом происходившей тогда промышленной революции. Однако по той же причине диссипацию рассматривали тогда лишь в связи с исчерпанием доступной энергии.
Интересно, что один из великих древнегреческих философов,. Платон, был глубоко убежден в том, что как постоянство, так и изменчивость являются составными частями реальности. Однако в XIX в. возникла конфликтная ситуация. Так, в физике необратимость и диссипация воспринимались как некоторая деградация, а, с другой стороны, биологическая эволюция, очевидно, также являющаяся необратимым процессом, ассоциировалась. с возрастанием сложности. Возможно, благодаря своему технологическому значению механика жидких сред исторически оказалась первой областью, в которой была полностью осознана решающая роль диссипативных процессов. Однако, по мере того как постепенно утверждалась молекулярная концепция строения вещества, аналогичная тенденция получила развитие в науке, химической кинетике, теории броуновского движения и различных типах транспортных явлений. Сегодня уже общепризнано, что диссипативные системы представляют собой весьма широкий и важный класс естественных систем.
Ярче всего различие между консервативными и диссипативными системами проявляется при попытке макроскопического описания последних, когда для определения мгновенного состояния системы используются такие коллективные переменные, как температура, концентрация, давление, конвективная скорость и т. д. При рассмотрении уравнений, управляющих поведением этих переменных, выясняется следующая их важная особенность: они не инвариантны относительно операции обращения времени в отличие от уравнени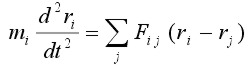й
и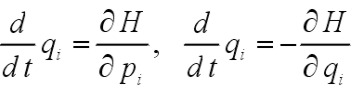 
.
На этой основе можно ожидать, что
чередование соответствующих событий будет необратимым.
Эта ситуация удивительно ярко
иллюстрируется на примере химической реакции. Рассмотрим процесс, описываемый
уравнением 
. Скорость расходования частиц типа А пропорциональна частоте
встреч молекул типов А и В, которая в случае разбавленных систем пропорциональна
произведению их концентраций. Таким образом, имеем
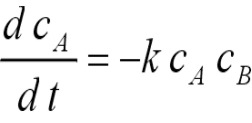(1)
, 
для концентраций в
зависимости от времени уравнение (1) принимает вид:
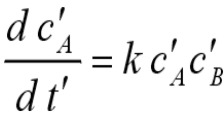
Теперь это уравнение описывает
процесс, в котором вещество типа А не расходуется, а производится. Разумеется,
такой процесс неэквивалентен описываемому уравнением (1).
В качестве дальнейших примеров
диссипативных процессов можно рассмотреть теплопроводность и диффузию. Как
показывает эксперимент, если в однородной жидкости возникает небольшая
неоднородность, то такое возмущение со временем расплывается и постепенно
исчезает. Аналогичная одонозначно направленная эволюция наблюдается в случае
небольшого изменения температуры, внесенного быстро и локально в изотермическую
жидкость. Количественное описание этих явлений, блестяще согласующееся с
опытными данными, дается следующими уравнениями, называемыми соответственно
уравнением Фика и уравнением Фурье:
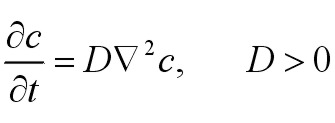(2)
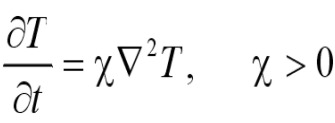(3)
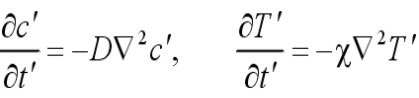
Как концентрация, так и температура являются примерами "четных" переменных, поскольку знак этих переменных при обращении времени не меняется. Напротив, импульс частиц или конвективная скорость жидкости являются "нечетными" переменными, поскольку они являются производными по времени от переменных типа координаты и меняют знак при обращении времени. Это приводит к следующему общему свойству уравнения эволюции диссипативной системы. Обозначим полный набор макроскопических переменных такой системы
. Эволюция этих
переменных во времени будет описываться системой уравнений:
, соответствующая четной переменной 
должна содержать инвариантную часть, в то время как функция скорости ,
соответствующая нечетной переменной , должна содержать
часть, меняющую знак при обращении времени. Примеры функций скоростей первого
класса дают правые части уравнений (1)—(3), примером же второго класса является
вклад вязкости в уравнение баланса импульса жидкости, участвующей в конвективном
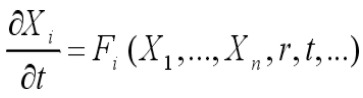
движении. Как и в случае консервативных систем, для диссипативных систем также можно ввести удобное фазовое пространство. Оно включает в себя ансамбль имеющихся переменных и поэтому становится бесконечномерным пространством в случае непрерывной среды, где различные характеристики являются пространственно распределенными величинами [см. уравнения (2) и (3)]. Поэтому удобнее всего работать с фазовым пространством, когда оно содержит дискретное число переменных, и в особенности когда это число конечно и, желательно, невелико.
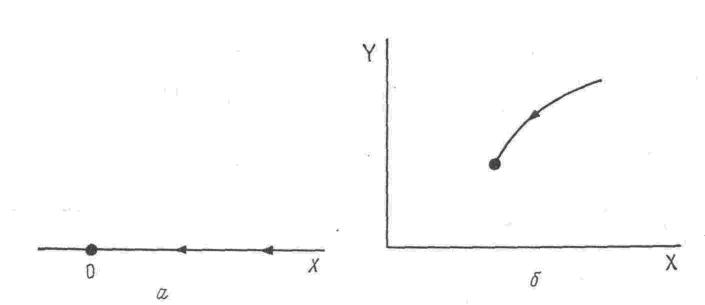
Рис. 1. Представление диссипативной системы
в фазовом пространстве,
а — система, описываемая одной переменной в соответствии с уравнением
(1),
б—система с
двумя переменными, уравнение (5).
(4)
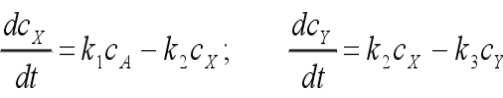(5)Фазовые траектории для такой системы показаны на рис. 1, б. Полезно иметь в виду, что некоторые диссипативные системы можно преобразовать к консервативному виду и привести их к гамильтоновой форме. Примером может служить знаменитый механизм Лотки—Вольтерра
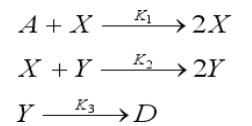(6)Пока еще не рассматривался вопрос о связи между диссипативными и консервативными системами, а также вопрос о возможности перехода от одного описания к другому.
Диссипативные
структурыДиссипативные структуры можно разделить на:
- временные
- пространственные
- пространственно-временные
Развитие турбулентности начинается при достижении числом Рейнольдса критического значения. Ламинарное течение становится неустойчивым, возникают стационарные колебания скорости движения, затем более сложное движение до, все увеличивающимся числом характерных частот. Это чрезвычайно сложное квазипериодическое движение иногда называют
Примерами пространственно-временных структур являются режим генерации лазера и колебательные химические реакции. Возникновение когерентного излучения в лазере происходит при достижении мощности накачки (подводимой энергии) порогового значения. Атомы или молекулы рабочего тела лазера, излучавшие до этого независимо друг от друга, начинают испускать свет согласованно, в одной фазе.
Фазовый переход в физике означает скачкообразное изменение физических свойств при непрерывном изменении внешних параметров. Неравновесный фазовый переход определяется флуктуациями. Они нарастают, увеличивают свой масштаб до макроскопических значений. Возникает неустойчивость и система переходит в упорядоченное состояние. Неравновесные фазовые переходы различной природы имеют общие характеристики. Прежде всего, упорядочение связано с понижением симметрии, что обусловлено появлением ограничений из-за дополнительных связей (корреляций) между элементами системы. Л. Д. Ландау в 1937 г. предложил общую трактовку фазовых переходов 2-го рода как изменение симметрии. В точке перехода симметрия меняется скачком. Также общим свойством кинетических фазовых переходов является наличие фундаментальной макроскопической переменной, позволяющей дать единое описание процесса упорядочения — параметра порядка. По своему физическому смыслу параметр порядка – это корреляционная функция, определяющая степень дальнего порядка в системе.