Кое-что о Байесе, статистике и подходах

Глава из книги «Как измерить все, что угодно. Оценка стоимости нематериального в бизнесе»
Издательство «Олимп-Бизнес»

Главное допущение, которое делается в большинстве вводных курсов статистики, заключается в следующем: единственное, что вы знаете о некоей генеральной совокупности, — это образцы, которые вы собираетесь из нее выбрать. Но на практике это допущение почти всегда неверно.

Предположим, что вы отбираете несколько торговых представителей для опроса на тему, существует ли связь между произошедшим недавно ростом продаж и проведенной ранее рекламной кампанией. Вы хотите оценить «вклад рекламной кампании в объем продаж». Для этого можно просто опросить весь торговый персонал. Но ведь изначально вы знаете больше, чем то, что расскажут вам эти люди. Вам и до опроса было кое-что известно о прошлой динамике продаж и об эффекте, который давали рекламные компании. Вы имеете сведения о сезонных колебаниях объема сбыта, влиянии экономического цикла и роли мер по повышению доверия потребителей. Имеет ли это какое-либо значение? Интуитивно мы понимаем, что предварительные данные также должны учитываться. Но пока студенты не доберутся до последних разделов своего учебника, им так и не расскажут, что нужно делать с этим знанием.

Парадокс предварительного знания

1. Вся традиционная статистика исходит из того, что наблюдатель ранее не располагал никакой информацией об объекте наблюдения.

2. В реальном мире данное допущение почти никогда не выполняется.

Проблему прежних знаний изучает так называемая байесовская статистика. Автор этого метода — Томас Байес, британский математик и пресвитерианский священник XVIII века, самые известные работы по статистике которого были опубликованы только после его смерти. Байесовская статистика занимается вопросом: как мы корректируем свое предварительное знание с учетом новой информации? Байесовский анализ начинается с того, что известно сейчас, и затем рассматривает, как это знание изменится с получением новых сведений. А небайесовская статистика, преподаваемая в большинстве курсов по методам выборочного наблюдения, исходит из следующего: все, что известно о некоей группе объектов, — это выборка, которую вы только что из нее сделали.

Фактически, именно байесовский анализ лежит в основе большинства иллюстраций, приведенных мною в главе 9, в том числе таблицы для определения 90-процентного CI без математических расчетов. Например, составляя рисунок 9.2, изображающий 90-процентный CI для доли в генеральной совокупности при малой выборке, я сначала предположил, что, если нет иных данных, внутри подгруппы значения этого CI распределены от 0 до 100% равномерно. Рассчитывая вероятность нахождения медианы по ту или иную сторону порогового значения, я начинал с исходного соображения: существует вероятность 50%, что истинная медиана генеральной совокупности лежит по одну из сторон от порога. И в том, и в другом случаях я исходил из максимальной неопределенности.

Теорема Байеса гласит, что вероятность наступления «события» при условии проведения «наблюдения» равна произведению вероятности наступления события и вероятности проведения наблюдения при условии наступления события, деленному на безусловную вероятность проведения наблюдения (см. рис. 1).

Предположим, решается вопрос о выпуске нового продукта. Согласно данным за прошедшие периоды, новые продукты приносили прибыль в первый год только в 30% случаев. Математик записал бы это утверждение следующим образом: P(FYP ¹) = 30%, то есть вероятность получения прибыли в первый год выпуска продукта составляет 30%. Нередко до старта массового производства осуществляется тестирование сбыта. Для всех случаев, когда новый продукт дал прибыль уже в первый год реализации, пробные продажи были удачными (под удачными продажами мы подразумеваем достижение определенного порогового объема реализации) только на 80%. Математик записал бы это следующим образом: P(S|FYP) = 80%, то есть «условная» вероятность успеха тестирования сбыта (S, successful — успешный) при условии, что производство продукта оказалось прибыльным уже в первый год (черта «|» означает «при условии»), равна 80%.

Рис. 1. Теорема Байеса

Однако значение вероятности успеха пробных продаж при условии, что производство данного продукта принесло прибыль в первый же год, — вовсе не тот показатель, который нас интересует. Что мы в действительности хотели бы знать, так это вероятность получения прибыли в первый же год при условии, что тестирование сбыта окажется удачным. Таким способом рынок подскажет нам, стоит ли запускать серийное производство продукта. Данный вопрос и позволяет выяснить теорема Байеса. Перепишем уравнение теоремы Байеса, подставив в него следующие обозначения интересующих нас функций:

• P(FYP|S) — вероятность получения прибыли в первый же год при условии удачного тестирования сбыта, иными словами, вероятность наступления события FYP при условии S;
• P(FYP) — «безусловная» вероятность получения прибыли в первый же год;
• P(S) — «безусловная» вероятность удачного тестирования сбыта;
• P(S|FYP) — вероятность удачного тестирования сбыта при условии получения прибыли в первый же год.

Допустим, что пробные продажи были удачны в 40% случаев. Чтобы рассчитать вероятность получения прибыли от продукта в первый же год при условии удачного тестирования сбыта, перепишем приведенное выше уравнение следующим образом:

P(FYP|S) = P(FYP) х P(S|FYP)/ P(S) = 30% x 80%/40% = 60%.

Если пробный рынок показал успех, то вероятность получения прибыли в первый же год составляет 60%. Заменив два числа в уравнении, мы можем рассчитать и вероятность получения прибыли в первый же год в случае неудачных пробных продаж. Как было показано, вероятность успеха тестирования реализации прибыльного продукта 80%. Поэтому вероятность провала пробных продаж равна 20%. Это можно записать следующим образом: P(~S|FYP) = 20%. Аналогично, если вероятность удачных пробных продаж всех продуктов 40%, то общая вероятность неудачи, или P(~S), равна 60%. Заменив в нашем уравнении P(S|FYP) и P(S) на P(~S|FYP) и P(~S), получим:

P(FYP|~S) = P(FYP) х P(~S|FYP) / P(~S) = 30% х 20%/60% = 10%.

Таким образом, провальный результат тестирования рынка дает вероятность получения прибыли в первый же год в размере всего 10%.

Иногда, не зная вероятности получения некоего результата, мы можем оценить вероятности других событий и затем рассчитать на их основе нужный показатель. Предположим, что данных о коэффициенте успеха тестирования рынка в прошедшие периоды у нас нет, так как это первые пробные продажи. Мы можем рассчитать данную величину на основе других. Калиброванный эксперт уже оценил P(S|FYP) — вероятность успешных пробных продаж продукта, который принесет прибыль в первый же год: P(S|FYP) = 80%. Допустим теперь, что эксперт оценил и вероятность удачных пробных продаж продукта, выпуск которого окажется в итоге убыточным (классическим примером может служить «New Coke»): P(S|~FYP) = 23%. Как и ранее, мы знаем, что вероятность прибыли от продукта в первый же год P(FYP) составляет 30%, значит, вероятность того, что это не случится, P(~FYP) будет равна 70% — [1 — P(FYP)]. Если мы суммируем произведения каждой условной вероятности на вероятность выполнения данного условия, то получим общую вероятность наступления данного события. Тогда:

P(S) = P(S|FYP) х P(FYP) + P(S|~FYP) х P(~FYP) = = 80% х 30% + 23% х 70% = 40%.

Этот этап может оказаться очень полезным, потому что в некоторых случаях расчет вероятности получения определенных результатов при определенных условиях прост и очевиден. Помогают такие вопросы, как: «Если к данной группе действительно относятся только 10% всех объектов генеральной совокупности, то какова вероятность того, что из 12 случайно выбранных человек пятеро будут принадлежать к этой группе?» или: «Если медиана затрат времени на анализ жалоб потребителей составляет более часа, то какова вероятность того, что временные затраты 10 из 20 случайно выбранных человек окажутся менее часа?»

В каждом из этих примеров мы можем рассчитать вероятность наступления события А при условии наступления события В, если знаем эти вероятности и вероятность наступления события В при условии наступления события А. Данный математический прием называется байесовской инверсией, и те, кто начинает использовать его в одной области, быстро обнаруживают применимость инверсии и во многих других сферах. Особенно полезной байесовскую инверсию находят те, кто рассматривает проблемы измерения так же, как в свое время это делали Эмили, Энрико и Эратосфен. Более специальные вопросы, связанные с инверсией, мы рассмотрим позднее, а пока попытаемся объяснить ее на интуитивном уровне. Ведь, возможно, и вы, сами того не осознавая, уже применяли этот прием. Вполне вероятно, что вы обладаете врожденным байесовским инстинктом.

Используйте свой природный байесовский инстинкт

Проблему иного качественного знания о выборочной совокупности, которым вы обладаете, не решают даже некоторые передовые методы статистики. В описанном ранее примере с рекламной кампанией вы могли бы проработать с людьми отдела сбыта весьма продолжительное время и узнать (и это знание было бы качественным), что Боб обычно оценивает ситуацию слишком оптимистично, Мануэль всегда все взвешивает, а Моника любит осторожничать. И, конечно, вы по-разному отнеслись бы к мнениям того сотрудника, которого знаете очень хорошо, и новичка. Как статистика учитывает эти знания? Если отвечать односложно, то она их вообще не учитывает, во всяком случае, тот ее вводный курс, который изучают тысячи людей.

К счастью, существует способ справиться с этой проблемой, причем намного более простой, чем любой раздел статистики за первый семестр. Назовем его инстинктивным байесовским подходом, суть которого заключается в следующем:

1) сначала нужно дать объекту (явлению) свою калиброванную оценку;

2) затем необходимо собрать дополнительную информацию (провести опрос, изучить работы других исследователей и т.д.);

3) далее нужно чисто субъективно скорректировать свою калиброванную оценку без дополнительных расчетов.

Я называю это инстинктивным байесовским подходом, так как есть основания считать, что когда люди получают новую информацию и уточняют свои прежние знания, они делают это способом, который можно охарактеризовать как байесовский. В 1995 г. психологи-бихевиористы Калифорнийского технологического института Махмуд А. Эль-Гамаль и Дэвид М. Гретер изучали, как люди учитывают первоначальные знания и новые сведения, оценивая вероятность каких-либо событий. Они попросили группу из 257 студентов угадать, из какого из двух лотерейных барабанов были извлечены шарики. В каждом барабане находились шарики, помеченные буквами «N» и «G». В одном барабане их было поровну, а в другом шариков с буквой «N» было больше. Шарики вынимались шесть раз, и студентам объявляли, сколько всего шариков каждого вида было вынуто.

Итак, задача состояла в том, чтобы определить, из какого барабана были взяты шарики. Студент, который видел, что в выборке из шести шариков, например, пять с буквой «N» и только один с буквой «G», мог решить, что они взяты из барабана с преобладанием шариков, помеченных буквой «N». Однако перед каждым извлечением шести шариков присутствующим говорили, что сами барабаны выбираются случайным образом с вероятностью один к двум, один к трем и два к трем. И вот ответы студентов показали, что они как будто интуитивно использовали байесовскую инверсию и при этом слегка переоценивали значение новой и недооценивали значение старой информации. Иными словами, они не были идеальными байесианцами, но все же, скорее, были ими.

Я также думаю, что будь на их месте калиброванные оценщики, они проявили бы байесианские качества лучше. Ведь студенты, принимавшие участие в исследовании, как и большинство обычных людей, были слишком уверены в своих ответах. А калиброванный специалист, не будучи слишком самоуверенным, все же обладал бы этим базовым байесовским инстинктом.

В нескольких построенных мною моделях использовались определенные калиброванными оценщиками условные вероятности самых разных событий. В 2006 г. я задал калиброванным экспертам из одной государственной структуры следующие пять вопросов.

A. Какова вероятность того, что через четыре года президентом будет демократ?

B. Какова вероятность того, что ваш бюджет через четыре года увеличится при условии, что президентом будет демократ?

C. Какова вероятность того, что ваш бюджет через четыре года увеличится при условии, что президентом будет республиканец?

D. Какова вероятность того, что ваш бюджет через четыре года увеличится?

E. Если ваш бюджет через четыре года увеличится, то какова вероятность того, что это произойдет в период президентства демократа?

Отвечая на эти вопросы, инстинктивный байесианец руководствовался бы теоремой Байеса. Если бы первые три вероятности (A, B и C) он оценил как 55, 60 и 40%, то, чтобы быть последовательным, четвертую и пятую вероятности (D и E) он должен был бы определить, соответственно, в 51 и 64,7%. Ответ на четвертый вопрос следовало бы записать так: A х B + (1 — A) х C, строго говоря, не из-за теоремы Байеса, а из-за необходимости правильно сложить условные вероятности. Иными словами, вероятность наступления некоего события равна вероятности выполнения некоего условия, умноженной на вероятность наступления данного события в случае выполнения этого условия, плюс вероятность того, что это условие не будет выполнено, умноженная на вероятность наступления этого события в случае невыполнения этого условия. Поэтому байесианец ответил бы на вопросы A, B, D и E таким образом, чтобы B = D / А х Е.

Это не всегда неочевидно, но, тем не менее, большинство калиброванных экспертов по принятию решений интуитивно дают ответы, удивительно близкие к удовлетворяющим этому требованию. Допустим, что в нашем последнем примере ответы калиброванного эксперта на вопросы A, B и С были 55, 70 и 40%. Но его ответы на вопросы D и E были 50 и 75%, хотя, по логике, при таких ответах на предыдущие вопросы они должны были быть 56,5 и 68,1%, а не 50 и 75%. На рисунке 2 мы показываем, как субъективные ответы на эти вопросы соотносятся с расчетными байесовскими значениями.

Обратите внимание: для того, чтобы согласовываться с другими субъективными ответами, одно из пары байесовских значений должно быть меньше нуля, а другое — больше 100%. Очевидно, что эти значения противоречили бы здравому смыслу, но когда калиброванные эксперты давали свои субъективные оценки, они не знали, что возникнет такая проблема. Однако в большинстве случаев полученные ответы оказались даже более близкими к «собственно байесовским», чем ожидали калиброванные эксперты (см. рис. 2).

На практике для того, чтобы сделать субъективные калиброванные оценки условных вероятностей внутренне непротиворечивыми, я применяю специальный метод, который называю байесовской коррекцией. Я сообщаю калиброванным экспертам, какими могли быть байесовские ответы на некоторые вопросы с учетом их ответов на другие вопросы. Затем они меняют свои оценки до тех пор, пока все их субъективные калиброванные вероятности не окажутся, по крайней мере, совместимыми друг с другом.

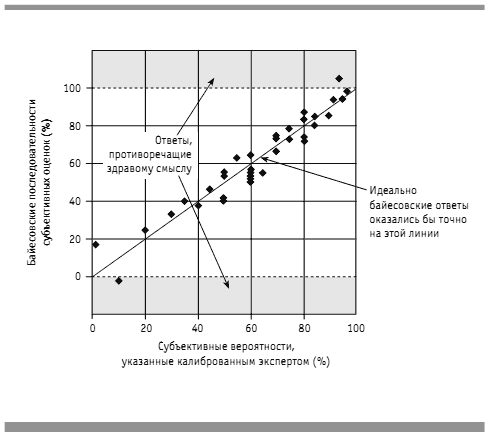
Рис. 2. Субъективные вероятности, указанные калиброванным экспертом, в сравнении с байесовскими вероятностями

Интересно, что, сравнивая новую информацию со старой, люди обычно мыслят максимально логично, что крайне важно, поскольку человек способен учитывать качественную информацию, не вписывающуюся в стандартную статистику. Например, при составлении прогноза возможного влияния новой политики на имидж компании в глазах общественности (что измеряется снижением числа жалоб потребителей, ростом доходов и т.п.) калиброванный эксперт должен был бы дополнить имевшиеся у него сведения «качественной» информацией о том, какую роль эта политика сыграла в других компаниях, результатами обсуждения в фокус-группах и т.д. Даже когда имеется
информация только о выборке, калиброванный специалист, обладающий байесовским инстинктом, принимает во внимание такую качественную информацию о выбранных объектах, которую не учитывают обычные статистические методы.

Убедитесь в этом сами, попытавшись ответить на следующий вопрос: увеличатся ли доходы вашей компании в следующем году? Укажите сначала свою калиброванную вероятность. Затем опросите двух-трех компетентных в этом вопросе сотрудников. Пусть они не только выскажут свое мнение, но и как-то его аргументируют, приведут какие-то детали. Теперь предложите другую субъективную вероятность того, что доходы компании увеличатся. Эта новая оценка наверняка будет отражать полученную вами новую информацию, даже если она и была по большей части качественной.

На рисунке 3 калиброванный эксперт (обладающий байесовским инстинктом и не страдающий как избытком, так и недостатком уверенности) сравнивается с тремя другими специалистами — использующим традиционные небайесовские методы выборки, такие какt-статистика, некалиброванным оценщиком и чистым байесовским оценщиком. Эта концептуальная схема показывает нам, как соотносятся с байесовским используемые ими подходы. Одна ось показывает, насколько специалисты уверены в своих оценках по сравнению с реальной вероятностью правильности их оценок, другая ось — насколько они учитывают предыдущую информацию.

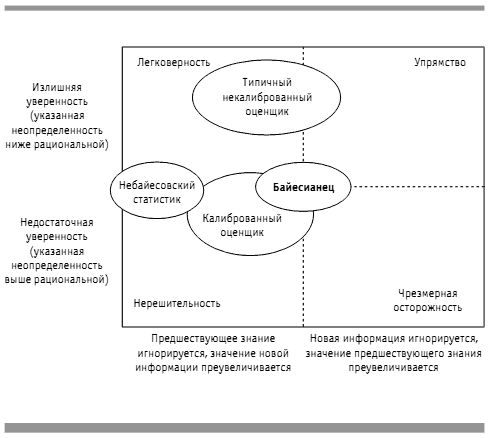
Рис. 3. Уверенность или информацияЖ разные акценты при проведении оценок

Метод может вызвать опасения тех, кто считает себя сторонником «объективного» измерения, но это беспокойство беспочвенно. Во-первых, я уже показал, что субъективные оценки калиброванных экспертов обычно ближе к разумным величинам, чем к противоречащим здравому смыслу. Во-вторых, этот метод работает там, где «объективная» статистика из первого семестра оказывается бесполезной и единственная альтернатива — вообще ничего не оценивать. В-третьих, те же самые люди постоянно бессознательно пользуются данным методом, принимая личные решения. Например, читая статью о возможном снижении цен на жилье, они принимают в результате решение купить или продать дом вовсе не потому, что используют приведенные в ней данные в своей модели, а потому, что извлекают из нее определенную качественную информацию.

В то же время существуют способы устранения тех недостатков, которые действительно имеются у описываемого метода. Ведь он опирается на субъективные суждения, что создает возможности для различного типа искажений, обсуждавшихся ранее. Вот некоторые приемы, позволяющие избежать искажений при использовании инстинктивного байесовского подхода.

• Отбирайте самых беспристрастных экспертов. Если от результатов исследования зависит бюджет отдела, не привлекайте его руководителя к качественной оценке новой информации.
• Проводите испытания вслепую. Иногда специалистам предоставляют необходимую информацию, скрывая от них, какую именно проблему они оценивают. Например, из стенограммы обсуждения нового продукта в фокус-группе удаляют все ссылки на этот продукт, с тем чтобы судьи определяли лишь то, позитивна или негативна реакция группы.
• Разделяйте обязанности. Этот прием хорошо сочетается с испытаниями вслепую. Пусть одна группа экспертов оценит качественную информацию, а вторая группа, изучив выводы первой и не зная, о каком конкретно продукте, отделе, проекте и т.д. идет речь, даст окончательный байесовский ответ.
• Помните о байесовских последствиях. Просите экспертов указать заранее, как определенные результаты могут повлиять на их оценки, и применяйте байесовскую поправку до тех пор, пока они не окажутся внутренне непротиворечивыми.

Неоднородный бенчмаркинг и его использование для оценки «ущерба бренду»

Все, что вам нужно представить в количественной форме, можно каким-то образом измерить. В любом случае это даст лучший результат, чем если не проводить измерений вовсе.

Закон Гилба

Одна из трудностей, с которыми столкнулись эксперты в задаче по определению среднего веса леденца, заключалась в невозможности сравнить его с весом другого объекта для наглядности. Один эксперт заявил: «Не представляю себе, как может выглядеть один грамм леденцов», а другой отметил: «Я вообще плохо определяю на глаз вес маленьких предметов».

А что, если я подсказал бы им: визитная карточка весит примерно 1 г, 10-центовая монета — 2,3 г, а большая скрепка для бумаги — ровно 1 г? Помогло бы это сузить диапазоны предлагаемых ими значений? Кое-кому это было очень полезно, особенно если первоначально указанный ими диапазон был достаточно широким. Получив мою информацию, один человек, который сначала считал, что верхняя граница диапазона может составлять 20 г, сразу же опустил ее до 3 г. Люди корректируют свои оценки потому, что, как мы теперь знаем, все они, особенно калиброванные оценщики, являются интуитивными байесианцами. Они склонны довольно рационально обновлять первоначальную информацию, которой обладали, учитывая новые сведения, даже если те носят качественный характер или имеют к оцениваемому объекту отдаленное отношение.

Я называю этот метод обновления прежнего знания, основанный на сравнении с другими, непохожими, но неким образом связанными с объектом предметами, «неоднородным бенчмаркингом». Когда люди не могут представить себе, как выглядит какая-то величина, подобная информация о масштабе, пусть даже относящаяся к другим предметам, может оказаться очень полезной. При оценке возможного спроса на ваш продукт в новом городе вам пригодятся данные о спросе на него в других городах и даже сравнительные данные об экономическом уровне разных городов.

Представление о порядке величин

Неоднородный бенчмаркинг — метод, при котором калиброванным экспертам, оценивающим неизвестную величину, предоставляют в качестве ориентиров другие количественные показатели, даже если связь между ними и кажется отдаленной.

Пример: прогнозирование продаж нового продукта на основе информации о сбыте других товаров или аналогичных конкурентных продуктов.

Неоднородный бенчмаркинг проводился, в частности, в нашем примере с информационной безопасностью. Можно моделировать разные риски для безопасности, используя диапазоны значений и вероятности. Но похоже, что область информационной безопасности — неисчерпаемый источник как курьезных представлений о неизмеряемости многих вещей вообще, так и примеров подобных «нематериальных» объектов. Одна из таких неизмеримых величин — «мягкие» затраты, которыми чреваты определенные катастрофические события.

Кому не раз доводилось сталкиваться с сопротивлением проведению измерений в области информационной безопасности, так это Питеру Типпетту из компании Cybertrust. Работая над своим дипломом и кандидатской диссертацией по биохимии, он сделал то, что не пришло в голову никому из его сокурсников: создал первую антивирусную программу, получившую впоследствии известность как Norton Antivirus. Затем Типпетт провел ряд исследований с участием сотен организаций с целью сравнительной оценки рисков для разных угроз безопасности. Казалось бы, мнению такого человека об измеряемости безопасности, безусловно, можно доверять. Тем не менее у многих специалистов в сфере IT сама идея проведения подобных измерений, похоже, вызывает острое неприятие.

Типпетт предложил свой подход к решению проблемы, состоящий в том, чтобы задаться вопросом: «Насколько ужасно будет, если...?» Согласно такому подходу, специалисты по информационной безопасности решают, существует ли малейшая вероятность наступления такого катастрофического события, которое необходимо предотвратить любой ценой. Типпетт замечает: «Поскольку катастрофа может произойти в любой области, превентивные меры должны приниматься везде. Думать о приоритетах здесь не приходится». Он приводит следующий конкретный пример. «Одна компания из списка Fortune 20 выделила на реализацию 35 своих проектов в сфере информационных технологий 100 млн дол. Руководитель ее информационной службы захотел узнать, какие из проектов важнее, и получил от своих подчиненных ответ, что этого никто не знает и знать не может».

Одно из тех ужасных событий, наступление которых предвидит Типпетт, — это ущерб для бренда, ухудшение имиджа компании в глазах общественности. По мнению эксперта по безопасности, не исключено, что хакеры могут взломать сервер, украсть и использовать в своих целях какую-либо важную информацию — истории болезней из медицинского учреждения или данные о владельцах кредитных карт. Далее можно вообразить, что раз это происшествие так повредит имиджу компании, его необходимо предотвратить любой ценой и при любой, самой малой вероятности наступления такого события. Поскольку точно оценить вероятность такого ущерба или его сумму невозможно, это позволяет эксперту утверждать, что защита от хакеров так же необходима, как меры по предотвращению любой другой возможной катастрофы, и поэтому средства на защиту должны быть выделены без вопросов.

Но Типпетт не согласен с мнением, что масштабы проблемы ущерба для бренда и других нежелательных событий нельзя различить. Он предложил оценивать то, что объединяет гипотетические примеры ущерба бренду с реально имевшими место событиями. Например, он спрашивает, во что компании обошлись часовой сбой в работе электронной почты и другие нежелательные события. Затем следует новый вопрос: «Насколько велик этот ущерб по сравнению с...?» («примерно такой же», «вдвое меньше», «в 10 раз больше» и т.д.)

Специалисты Cybertrust уже получили некоторое представление о сравнительной шкале ущерба от различных нежелательных событий после анализа материалов экспертиз 150 случаев взлома баз данных о клиентах. В основном это были сведения о кражах данных карточек MasterCard и VISA.

Специалисты Cybertrust провели опросы руководителей компаний и широкой общественности по поводу восприятия ими ущерба бренду. Кроме того, они сравнили фактические убытки от снижения курса акций компании после подобных нежелательных событий. Благодаря этим опросам и сопоставлениям Типпетт сумел доказать, что ущерб бренду, нанесенный кражей хакерами клиентских данных, превышает потери от неправильного хранения резервной копии всей информации.

Сравнение с несколькими ориентирами позволило выявить разницу в масштабе ущерба от разных типов катастроф. Какой-то ущерб бренду был больше урона от одних событий, но меньше потерь от других. Более того, появилась возможность рассчитать «ожидаемые» убытки на основании относительных уровней потерь и их вероятностей.

Заслугу Типпетта в решении данной проблемы переоценить невозможно. До его исследований компании даже не представляли, насколько большим может быть ущерб бренду, даже порядка этой величины. А теперь они, по крайней мере, могут оценить масштабы вопроса и понимают значение снижения различных угроз безопасности.

Сначала руководство одной компании — клиента Типпетта — отнеслось к его результатам с известным недоверием, но, как пишет он сам, через год число скептиков сократилось до одного, а все остальные уже стали его сторонниками. Наверное, оппонент Типпетта продолжал утверждать, что устранить неопределенность по этому вопросу не смогут никакие наблюдения. Но когда приходится оценивать такие явления, как возможный ущерб бренду, неопределенность обычно столь высока, что определение одного только масштаба чисел уже позволяет ее снизить, а значит, и провести измерение.

Конечно, ваша компания вряд ли станет проводить опросы в 100 других организациях, чтобы осуществить нужную оценку. Но в этом и нет необходимости, так как они уже были проведены и Cybertrust продает полученные результаты. К тому же использование этого метода даже внутри компании позволяет сократить неопределенность независимо от того, купит ваша компания результаты внешних исследований или нет.

Применение метода неоднородного бенчмаркинга

Неоднородный бенчмаркинг — идеальный способ оценки «мягких затрат» на преодоление последствий катастрофических событий, особенно в условиях, когда первоначальная неопределенность чрезвычайно высока. Примерами таких событий могут служить:

• кража хакерами данных кредитных карт и карт социального страхования,
• случайное обнародование персональных медицинских данных,
• массовый отзыв продукта из продажи,
• крупная авария на химическом заводе,
• корпоративный скандал.

Может показаться, что мы уделяем слишком много внимания информационной безопасности, но ведь данный метод может применяться в самых разных областях. Он не только годится для оценки ущерба от нарушения безопасности, но и позволяет определить приоритетность инвестиций, необходимых для предотвращения корпоративного скандала, катастрофы на химическом предприятии и т.п. На самом деле метод может использоваться и для оценки положительных последствий каких-либо событий. Какова стоимость того, что наш товар будет считаться эталоном высокого качества в отрасли? Бенчмаркинг — практичный способ определить масштабы проблемы в случаях, когда неопределенность так высока, что устранить ее кажется совершенно невозможно.

Если подобное использование ориентиров кажется «слишком субъективным», вспомним о цели нашего измерения в данном случае. Что такое ущерб бренду, как не восприятие? Ведь мы оцениваем не физическое явление, а мнения людей. Такая оценка невозможна без понимания того, что ущерб бренду — это, по определению, изменение представлений потребителей. И вы определяете размеры этого ущерба, опрашивая потребителей. С другой стороны, можно проследить, что покупатели делают со своими деньгами, наблюдая за тем, как неблагоприятное событие повлияло на курс акций или объем продаж. В любом случае ущерб бренду оказывается измеренным.

Кое-какие тонкости: байесовская инверсия для диапазонов

Как уже упоминалось, в основе многих рисунков и таблиц, составленных мной для этой книги, лежит байесовская инверсия. Решая большинство статистических задач и задач по измерению, мы спрашиваем: «Какова вероятность того, что истинное значение данной величины равно X при условии, что я видел то-то и то-то?» Но вообще-то легче ответить на вопрос: «Если истинное значение равно X, то какова вероятность увидеть то, что я видел?» Байесовская инверсия позволяет нам ответить на первый вопрос, ответив сначала на второй. Нередко ответить на последний бывает намного легче.

Сразу хочу предупредить, что далее нам придется коснуться специальных вопросов. Если вы захотите пропустить это описание, то электронную таблицу для байесовской инверсии, составленную в том числе и на основе приводимого ниже примера, вы найдете на вспомогательном веб-сайте: www.howtomesureanything.com, выбрав связь «Bayesian Inversion» («Байесовская инверсия»). Я постарался сделать это описание как можно проще. Расчеты могут показаться довольно длинными, но я свел их к минимуму, перейдя, где это было возможно, сразу к функциям Excel.

Итак, предположим, что у нас есть магазин автозапчастей и возникла необходимость определить коэффициент удержания покупателей. Мы подозреваем о существовании проблемы с удовлетворенностью потребителей. Калиброванная оценка процента покупателей, которые захотят сделать в нашем магазине еще одну покупку, составляет 75—90% (доверительный интервал, как обычно, 90-процентный). Конечно, желательно, чтобы этот показатель был как можно выше, но если он не достигнет 80%, нам придется принять ряд весьма дорогостоящих корректирующих мер. Расчетная стоимость этой информации намного превышает 500 тыс. дол., но мы, естественно, постараемся минимизировать затраты на проведение опросов потребителей, переложив часть их на плечи своих покупателей. Помня о поэтапном определении интересующего нас показателя, выберем сначала всего 20 потребителей и посмотрим, какую информацию удастся получить. Если из этой выборки 14 человек скажут, что придут к нам за покупками еще, то как мы изменим первоначальный диапазон? Помните, что типичные параметрические, небайесовские методы не позволяют учитывать его при расчетах.

Начнем с более простого вопроса: если 90% покупателей скажут, что вновь придут за запчастями в наш магазин, то сколько человек из 20 сказали бы то же самое? Ответ очевиден — 90% от 20, или 18 человек. Если бы таких людей было 80%, то в нашей выборке их оказалось бы 16. Конечно, мы знаем, что совершенно случайно в числе 20 выбранных нами покупателей желающих вернуться в магазин может оказаться 15 или даже 20 человек. Поэтому нужно узнать не только ожидаемый результат, но и вероятность его получения.

Чтобы определить вероятность получения конкретного результата, используем специальное, уже упоминавшееся распределение, которое называется биноминальным. Напомним, что биноминальное распределение позволяет рассчитать вероятность определенного числа «попаданий» при условии проведения определенного числа попыток и того, что в каждой попытке может быть только один результат. Например, при подбрасывании монетки «попаданием» можно назвать выпадение орла, попытками — подбрасывания, а шанс попадания составляет 50%. Предположим, например, что мы хотим узнать вероятность того, что при 10 подбрасываниях орел выпадет четыре раза при вероятности его выпадения 50%. Вместо того, чтобы объяснять всю формулу и теорию комбинаторики, я сразу перейду к формуле программы Excel. В Excel мы просто запишем:

= binomdist(число попаданий, число попыток, вероятность попадания, 0).

Взяв числа из нашего примера с подбрасыванием монеты, запишем: binomdist(4, 10, 0,5, 0), и Excel даст нам значение 20,5% (ноль в конце говорит о том, что нас интересует вероятность только этого конкретного результата. Записав вместо нуля единицу, получим накопленную вероятность, то есть вероятность указанного или меньшего числа попаданий). Данный результат означает, что есть 20,5-процентная вероятность того, что в случае 10-кратного подбрасывания монеты орел выпадет точно четыре раза.

В нашем примере с магазином автозапчастей покупатель, заявивший «да, я еще сюда вернусь», — это попадание, а размер выборки — это число попыток. Используя биноминальное распределение, менеджер может определить вероятность конкретного результата, например вероятность того, что среди 20 выбранных нами покупателей вернутся в магазин только 14, хотя вообще таких людей должно быть 90%. В Excel мы запишем: =binomdist(14, 20, 0,9, 0), что даст нам 88,7-процентную вероятность 14 попаданий при 20 случайно выбранных покупателях, если бы на самом деле 90% посетителей сказали, что готовы сделать еще одну покупку. Отсюда мы уже видим, что верхняя граница нашего первоначального диапазона не слишком правдоподобна.

Предположим теперь, что мы рассчитали эту вероятность для генеральной совокупности, в которой доля повторных покупателей составит сначала 75%, затем 76, 77 и т.д. вплоть до 90% (таким образом, шаг равен 1%). Используя некоторые таблицы в программе Excel, мы сможем быстро рассчитать вероятность конкретного результата при данном «истинном» проценте повторных покупателей. Для каждого приращения на 1% получим вероятность того, что 14 из 20 покупателей ответят утвердительно на вопрос о возвращении за повторной покупкой при данном «истинном» проценте повторных покупателей. Я бы рассчитывал эти вероятности для каждого приращения на 1%, начиная от 60% (что с учетом нашего 90-процентного CI маловероятно, но возможно) и заканчивая 100%. Для каждого приращения проведем расчет на основе теоремы Байеса. Запишем все это вместе в следующем виде:

P(Prop = Х|Попадания = 14/20) = P(Prop = X) х х Р(Попадания = 14/20|Prop = х) / P(Попадания = 14/20),

где

P(Prop = Х|Попадания = 14/20) — вероятность данного процента повторных покупателей в генеральной совокупности (процента X) при условии, что 14 из 20 случайно отобранных объектов являются попаданиями;

P(Prop = X) — вероятность того, что определенный процент покупателей в генеральной совокупности вернется снова (например, X = 90% генеральной совокупности покупателей, которые действительно сказали, что вернутся снова);

P(Попадания = 14/20|Prop = X) — вероятность 14 попаданий из 20 случайно выбранных объектов при данном проценте (проценте X) повторных покупателей в генеральной совокупности;

P(Попадания = 14/20) — вероятность получения 14 попаданий из 20 попыток при условии, что все возможные проценты повторных покупателей в генеральной совокупности находятся в первоначальном диапазоне.

Мы знаем, как рассчитать Р(Попадания = 14/20|Prop = 90%) в Excel: [=binomdist(14, 20, 0,9, 1)]. Теперь нам нужно придумать, как рассчитать P(Prop = X) и Р(Попадания = 14/20). Мы можем рассчитать вероятность каждого приращения на 1% доли повторных покупателей в нашем диапазоне, вернувшись снова к функции =normdist() в Excel и используя калиброванную оценку. Например, чтобы получить вероятность того, что 78—79% наших покупателей окажутся повторными (или, по крайней мере, заявят об этом во время опроса), мы можем записать следующую формулу Excel:

=normdist(0,79, 0,825, 0,0456, 1) — normdist(0,78, 0,825, 0,0456, 1).

Число 0,825 — это среднее значение нашего калиброванного диапазона: (75% + 90%)/2; 0,0456 — среднее квадратичное отклонение (как вы помните, в 90-процентном CI 3,29 среднего квадратичного отклонения): (90% — 75%)/3,29. Формула normdist дает нам разность между вероятностью получить менее 79% и вероятностью получить менее 78%, которая составляет 5,95%. Мы можем определить это для каждого приращения на 1% в исходном диапазоне, а затем рассчитать вероятность того, что доля повторных покупателей в генеральной совокупности равна X [то есть P(Prop = X)] для каждого мало-мальски вероятного значения X в нашем диапазоне.

Расчет значения P(Попадания = 14/20) основан на всем, что мы делали до сих пор. Чтобы рассчитать P(Y), когда мы знаем P(Y|X) и P(X) для каждого значения X, суммируем произведения P(Y|X) х P(X) для каждого X. Зная, как рассчитать P(Попадания = 14/20|Prop = X) и P(Prop = X) для любого X, мы просто умножаем эти две величины для каждого X, затем суммируем их и получаем, что P(Попадания = = 14/20) = 8,56%.

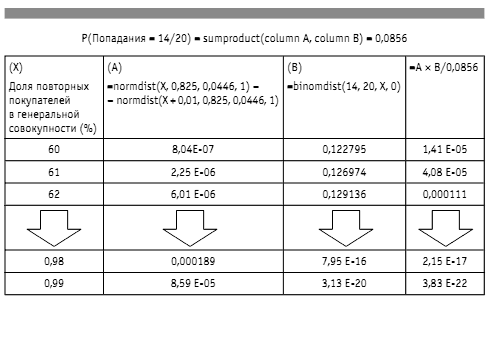
Теперь для каждого значения в исходном диапазоне (и даже немного за его пределами, чтобы получить «хвосты» в уравнении) мы рассчитываем P(Prop = X), P(Попадания = 14/20|Prop = X) и P(Prop == X|Попадания = 14/20), для каждого приращения на 1% повторных покупателей в генеральной совокупности величина P(Попадания == 14/20) для всех одинакова и равна 8,56% (см. табл. 1).

Значения в последнем столбце — вероятности данного процента повторных покупателей в их генеральной совокупности. Если суммировать накопленные значения в последнем столбце (складываем все предшествующие значения в строке), то выяснится, что итог составит около 5%, когда процент повторных покупателей достигнет 79%, и 95%, когда этот процент будет равен 85%. Это означает, что наш новый 90-процентный CI сократится до 79—85%. Это не слишком большое сужение первоначального диапазона (75—90%), но тем не менее достаточно информативное. Теперь, согласно накопленным значениям последнего столбца, вероятность того, что мы находимся ниже основного порога в 80%, составляет 61%. Эту электронную таблицу целиком можно найти на веб-сайте: www.howtomesureanything.com

Таблица 1. Отдельные строки из таблицы расчётов с использованием байесовской инверсии

Похоже, что удержание покупателей у нас не на высоте. Но мы пересчитаем стоимость этой информации, и хотя она уменьшится, окажется, что провести дополнительные измерения все равно имеет смысл. Выберем еще 40 покупателей, и тогда в сумме их будет 60 человек. Из этих 60 только 39 скажут, что вернутся в наш магазин. Наш новый 90-процентный CI окажется равным 69—80%. Теперь верхняя граница равняется нашему первоначальному критическому порогу 80%, давая 95-процентную уверенность, что доля повторных покупателей низка настолько, что требует от нас серьезных, дорогостоящих изменений.

Расчеты оказались довольно сложными, но помните, что вы можете воспользоваться таблицами, приведенными на нашем вспомогательном сайте. И вполне возможно, что в данном случае сработал бы обсуждавшийся ранее субъективный байесовский метод, применяемый калиброванными экспертами. Возможно, опрос покупателей выявит такие качественные факторы, которые сумеют учесть наши калиброванные специалисты. Однако стоимость результатов этих важных измерений достаточно высока, чтобы оправдать наши дополнительные усилия.

Избегайте «инверсии наблюдения»

Многие задают вопрос: «Какой вывод я могу сделать из этого наблюдения?» Но Байес показал нам, что нередко полезнее задать вопрос: «Что я должен наблюдать, если будет соблюдаться условие X?» Ответ на последний вопрос позволяет разобраться с первым.

Xотя на первый взгляд байесовская инверсия может показаться весьма трудоемкой, она относится к наиболее эффективным из имеющихся в нашем распоряжении методам измерения. Если удастся сформулировать вопрос «Какова вероятность увидеть X, если справедливо Y?» и превратить его в «Какова вероятность того, что справедливо Y, если мы наблюдаем X?», то можно решить огромное число задач по измерению. В сущности, именно так мы и находим ответы на большинство научных вопросов. Если предложенная гипотеза верна, то что мы должны наблюдать?

Напротив, многие менеджеры, похоже, считают, что все измерения сводятся к поиску ответов на вопрос: «Какой я должен сделать вывод из того, что вижу?» Когда кажется, что совершена ошибка наблюдения, люди решают: на этом основании делать выводы нельзя, какой бы низкой ни была вероятность такой ошибки. Однако байесовский анализ показывает, что воображаемые менеджерами ошибки крайне маловероятны и что измерение все равно заметно снизило бы существующую неопределенность. Иными словами, отсутствие, по крайней мере, теоретического понимания байесовской инверсии приводит к переворачиванию вопроса и к формированию убеждения, что маловероятные ошибки сводят ценность измерений к нулю — то есть к самой неудачной разновидности «инверсии наблюдения».

Примечания

¹ David M. Grether, Mahmoud A. El-Gamal. Are People Bayesian? Uncovering Behavioral Strategies // Social Science Working Paper 919, 1995, California Institute of Technology.

² Tom DeMarco, Timothy Lister. Peopleware: Productive Projects and Teams. 2nd ed. New York: Dorset House Publishing, 1999.

¹ FYP — first year profit, прибыль первого года. — Примеч. переводчика.

² Неточность: рисунок доли генеральной совокупности приведен в главе 9 (см. рис. 9.2). — Примеч. редактора.