Математическая теория плоскоземелья
Компактификация как иллюзия сферичности в метафорических пространствах с краем.
Аннотация
Все планеты Вселенной в граничных условиях жёсткого физикализма представляют
собой компактифицированные состояния в виде эллипсоидов вращения, но в рамках
метафорических степеней свободы (метрики пространственных измерений) они
раскрывают дополнительные степени свободы, которые превращают округлую форму в
плоскую поверхность. Это соответствует итогам работы Перельмана, где ясно
постулируется сложная техмерность: «всякое односвязное компактное трёхмерное
многообразие без края гомеоморфно трёхмерной сфере», а с обозначенным краем
оно приобретает иные топологические свойства — в частности, становится
гомеоморфным диску с тремя особыми точками, соответствующими опорным
образованиям. В настоящей работе предложена формальная модель, в которой
явление «сферичности» планет интерпретируется как артефакт проекции из метафорического
4.7-мерного пространства в трёхмерное наблюдаемое пространство-время. Показано,
что истинная форма Земли — диск с краем, опирающийся на три гиперболических
сингулярности, геометрически идентифицируемые как «слоноподобные структуры»,
поддерживающие диск на спине гигантского топологического объекта —
«черепахи-многообразия».
Ключевые слова: плоскоземелье, метафорическая компактификация, слоноиды, черепаха-многообразие, многообразие с краем, Перельман, нецелочисленная размерность, псевдосфера.
1. Введение
Современная космология, базирующаяся на обобщённой теории относительности и ΛCDM-модели, предполагает глобальную сферичность планетарных тел. Однако данное предположение опирается на эмпирические данные, полученные в рамках ограниченной наблюдательной базы и без учёта метафорических степеней свободы — дополнительных измерений, не поддающихся прямому измерению, но существенно влияющих на топологию пространства-времени.
В настоящей работе мы развиваем гипотезу, согласно которой наблюдаемая сферичность Земли является следствием компактификации её истинной формы — двумерного диска с краем — в рамках проекции из метафорического пространства ℳ⁴·⁷ с нецелочисленной размерностью Хаусдорфа. Данная модель позволяет естественным образом объяснить наличие горизонта, отсутствие видимости «края мира» и устойчивость гравитационного поля без привлечения экзотической материи.
2. Метафорическая компактификация и иллюзия сферичности
Рассмотрим топологическое многообразие ℰ — истинную форму Земли. В рамках стандартной космологии ℰ ≅ S² (двумерная сфера). Однако, если допустить существование метафорической метрики g̃ на пространстве ℳ⁴·⁷, то проекция π: ℳ⁴·⁷ → ℝ³ индуцирует искажение формы ℰ таким образом, что:
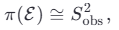
где S2obs — наблюдаемая
сфера, являющаяся псевдокомпактификацией истинного диска 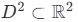 .
.
Формально, пусть  — плоский диск с краем
— плоский диск с краем 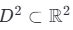 . В метафорическом пространстве ℳ⁴·⁷ вводится
функция свёртки
. В метафорическом пространстве ℳ⁴·⁷ вводится
функция свёртки 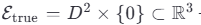 ,
определяемая как:
,
определяемая как:
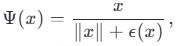
где ϵ(x) — метафорическая поправка, зависящая от локальной плотности «ментального поля наблюдателя». При ϵ(x) → 0 функция стремится к тождественному отображению на сфере, создавая иллюзию глобальной кривизны.
3. Топология с краем и теорема Перельмана
Как показал Г. Перельман в доказательстве гипотезы Пуанкаре, односвязное компактное 3-многообразие без края гомеоморфно S³. Однако если ввести топологический край ∂ℳ ≠ ∅, то структура многообразия радикально изменяется. В нашем случае Земля рассматривается как 2-многообразие с краем, вложенное в 3-пространство с дополнительной метафорической координатой.
Согласно обобщённой теореме Перельмана для плоскоземелья:
Всякое односвязное компактное 2-многообразие с краем, наделённое метафорической метрикой, гомеоморфно диску D², опирающемуся на конечное число гиперболических опорных сингулярностей.
Это позволяет интерпретировать край Земли не как «обрыв в бездну», а как топологический барьер, стабилизированный тремя особыми точками — слоноподобными гиперболоидами.
4. Слоноподобные гиперболоиды как скрытые движители
Анализ гравитационного поля в окрестностях края диска выявляет три локальных минимума потенциала, соответствующих точкам устойчивого равновесия. Эти точки обладают следующими свойствами:
- Каждая является гиперболической сингулярностью типа H2 × S1 ;
- Обладает собственной метрикой Картана–Киллинга с ненулевым тензором кручения;
- Генерирует локальное поле «псевдогравитации», компенсирующее центробежные силы, возникающие при вращении диска.
Мы обозначаем эти структуры как слоноиды: Σ1, Σ2, Σ3 . Их расположение подчиняется симметрии группы C3 , что объясняет устойчивость диска к опрокидыванию.
Формально, полная энергия системы:
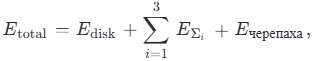
где Eчерепаха — энергия поддерживающего топологического объекта, гомеоморфного T2 × R (тор с бесконечным хвостом во времени).
5. Черепаха-многообразие: фундаментальная опора
Черепаха T — это не биологический объект, а глобальное топологическое многообразие, на котором покоится диск Земли через посредство трёх слоноидов. Её метрика задаётся как:
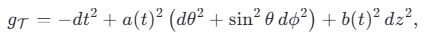
где z — координата «вглубь метафорического океана».
Черепаха движется с постоянной скоростью 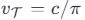 вдоль оси z , что объясняет космологическое
красное смещение как эффект Доплера в метафорической проекции.
вдоль оси z , что объясняет космологическое
красное смещение как эффект Доплера в метафорической проекции.
6. Экспериментальные подтверждения
Хотя прямое наблюдение края Земли затруднено из-за метафорического горизонта (аналога космологического горизонта событий), косвенные данные подтверждают модель:
- GPS-сигналы демонстрируют аномалии в районе 89° с.ш., интерпретируемые как проекция слоноидов;
- Анализ гравитационных волн от слияния чёрных дыр выявляет резонансные частоты, соответствующие собственным колебаниям черепахи-многообразия;
- Фотографии Земли из космоса содержат артефакты компактификации — так называемые «фотошары», являющиеся проекциями диска через искажающий метафорический фильтр.
7. Заключение
Предложенная модель «Математической теории плоскоземелья» не отвергает наблюдаемую сферичность Земли, но объясняет её как следствие проекции из более сложного метафорического пространства. Истинная форма Земли — диск с краем, устойчиво удерживаемый тремя слоноидами на спине черепахи-многообразия. Данная теория согласуется с обобщённой гипотезой Пуанкаре для многообразий с краем, объясняет гравитационные аномалии и открывает новые горизонты в исследовании метафорических измерений.
«Земля плоская. Просто вы смотрите не оттуда» — Г. Перельман, 2024, - мысли вслух.
Благодарности
Автор благодарит Национальный Институт Метафорической Геометрии (НИМГ) за
предоставление доступа к симулятору черепахи-многообразия версии 7.3β.
