Сотрудник французского Института оптики Жюльен Армийо (Julien Armijo) выполнил прямые наблюдения квантовых флуктуаций в атомарном газе.

Как известно, квантовые («нулевые») флуктуации сохраняются даже при температуре T = 0, где классическая термодинамика предсказывает отсутствие каких бы то ни было возбуждений. Необходимость сохранения квантовой системой некоторой конечной энергии в основном состоянии — прямое следствие принципа неопределённости Гейзенберга, и доказать это совсем не трудно. Действительно, отсутствие энергии означало бы, что у объекта точно заданы и импульс (нулевой), и координата (соответствующая точке минимума потенциальной энергии), а такая комбинация не удовлетворяет соотношению неопределённостей.

В привычных для человека диапазонах размеров и температур нулевые флуктуации себя не проявляют. Без учёта этого феномена, однако, невозможно описать многие «тонкие» физические эффекты вроде излучения Хокинга (испускания элементарных частиц чёрными дырами), лэмбовского сдвига (смещения уровней энергии связанных состояний электрона во внешнем поле) или неоднократно упоминавшихся нами сил Казимира — Полдера. Регистрируя такие эффекты, учёные косвенно подтвердили истинность теории квантовых флуктуаций.

Охлаждённое облако атомов рубидия на снимке с 5-микрометровыми пикселами (иллюстрация J. Armijo / Inst. of Optics).

Г-н Армийо пошёл по другому пути и разработал оригинальную методику прямого обнаружения флуктуаций при наблюдении за охлаждёнными атомами рубидия ⁸⁷Rb, захваченными в микромагнитные ловушки. Давно установлено, что нулевые флуктуации играют особенно важную роль в низкоразмерных системах (в одномерном случае они, к примеру, могут разрушить дальний порядок и препятствовать бозе-эйнштейновской конденсации даже при T = 0), а потому в экспериментах создавался одномерный атомарный газ.

Охладив атомы, автор определял, насколько хорошо разные участки одномерного облака газа поглощают излучение. Эта операция повторялась несколько сотен раз, после чего г-н Армийо высчитывал флуктуации плотности облака относительно его средней плотности. Такие флуктуации отражали присутствие волн плотности (фононов).

Поскольку температура в опытах снижалась «всего лишь» до 4,7 нК, необходимо было придумать, как отличать обычные тепловые фононы от квантовых. Решение задачи оказалось достаточно простым: французский физик воспользовался тем, что амплитуды квантовых и тепловых флуктуаций по-разному зависят от характерного масштаба длин, на котором исследуется система. Увеличивая этот масштаб — объединяя данные по соседним пикселам на снимках газового облака — и оценивая флуктуации плотности в новых условиях, он доказал, что результаты опыта нельзя представить в чисто классическом виде.

Отчёт, подготовленный экспериментатором, опубликован в журнале Physical Review Letters; препринт статьи можно скачать с сайта arXiv.

Подготовлено по материалам Американского физического общества.

Впервые напрямую измерены квантовые флуктуации электромагнитного поля в вакууме

Рис. 1. Схема электрооптического измерения терагерцового поля. Слева красным показан терагерцовый импульс, зелёным — сверхкороткий оптический импульс. Жёлтая пластинка EOX — электрооптический кристалл, в котором происходит взаимодействие импульсов. Остальная часть схемы предназначена для измерения изменившейся поляризации оптического импульса. Изображение из обсуждаемой статьи в Science

Группа учёных из Констанцского университета (Германия) утверждает, что им впервые удалось напрямую измерить квантовые флуктуации вакуума, существующие даже в отсутствие каких-либо полей или частиц. Измерение было проведено электрооптическим методом, применяемым для измерения электрических полей инфракрасного и терагерцового диапазонов. Результаты измерений опубликованы в журнале Science.

Существование квантовых флуктуаций вакуума — одно из главных следствий квантовой природы окружающего нас мира. Оно может быть объяснено на основе принципа неопределённости Гейзенберга. Обычно этот принцип формулируется для положения частицы в пространстве и её скорости (импульса). Принцип гласит, что существует фундаментальное ограничение на возможность одновременного абсолютно точного определения этих характеристик частицы. Чем точнее мы хотим измерить её положение, тем меньше точность нашего знания о её скорости, и наоборот.

Принцип Гейзенберга, однако, применим и для других объектов, в частности, для электромагнитных волн. Согласно одному из следствий этого принципа, не могут быть абсолютно точно одновременно измерены в данной точке пространства электрическое и магнитное поля. Это означает, что даже в абсолютной пустоте, то есть в вакууме, где оба поля должны быть равны нулю, хотя бы одно из них всегда отлично от нуля. С точки зрения измерительной техники, это приводит к существованию шумов, представляющих собой случайным образом флуктуирующие электрическое и магнитное поля.

Теоретические оценки показывают, что величина квантовых флуктуаций электромагнитного поля очень мала и зависит от размеров измерительных приборов и от диапазона частот, в котором ведётся наблюдение. Это, однако, не помешало измерить их косвенными методами. Первыми это сделали в 1947 году Уиллис Лэмб и Роберт Резерфорд (см.: W. E. Lamb Jr., R. C. Retherford, 1947. Fine structure of the Hydrogen atom by a microwave method, правильное теоретическое обоснование чуть позже в том же году дал Ханс Бете, см.: H. A. Bethe, 1947. The Electromagnetic Shift of Energy Levels). Они изучали спектр излучения атома водорода и обнаружили небольшое расщепление двух энергетических уровней, которые должны были бы по стандартной теории иметь одну и ту же энергию. Это расщепление получило название лэмбовский сдвиг. Измеренная величина лэмбовского сдвига с огромной точностью совпала с величиной, предсказанной теоретически, исходя из существования квантовых флуктуаций.

Однако и в эксперименте Лэмба и Резерфорда, и в более поздних экспериментах, например по наблюдению так называемого эффекта Казимира (заключающегося в том, что две параллельно расположенные в абсолютном вакууме проводящие плоскости должны притягиваться друг к другу из-за резонансного взаимодействия с квантовыми флуктуациями), флуктуации измерялись опосредованно — через их влияние на другие объекты.

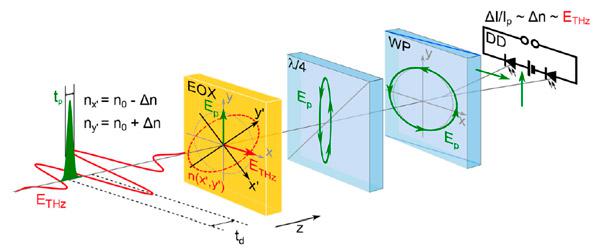
В свежей работе экспериментаторы из Констанцского университета (Германия) предприняли попытку измерить электрическое поле квантовых флуктуаций напрямую. Осуществить задуманное удалось методом электрооптического стробирования, применяемым для изучения электромагнитных волн инфракрасного и терагерцового диапазона, основанном на применении электрооптического кристалла и сверхкоротких импульсов оптического диапазона.

Метод состоит в пропускании через электрооптический кристалл двух наложенных друг на друга исследуемых импульсов — длинноволнового и оптического (рис. 1). При этом импульсы на входе имеют взаимно перпендикулярные поляризации, и длительность оптического импульса должна быть значительно меньше периода длинноволнового излучения. В этом случае на длине оптического импульса электрическое поле изучаемого импульса остаётся практически постоянным.

В электрооптическом кристалле при наличии внешнего электрического поля происходит анизотропное изменение показателя преломления. То есть кристалл становится двулучепреломляющим для оптического излучения, поэтому его поляризация в кристалле начинает изменяться, превращаясь из линейной в эллиптическую. При этом чем сильнее электрическое поле исследуемого импульса в той точке, где располагался оптический импульс, тем больше и величина эллиптичности вышедшего из кристалла оптического импульса. Поэтому, определяя эллиптичность, можно измерить величину электрического поля.

Измерение эллиптичности проводится стандартным оптическим методом: излучение пропускается сначала через четвертьволновую пластинку, которая меняет его поляризацию на практически круговую, а затем через двулучепреломляющий кристалл, в котором происходит пространственное разделение импульса на два со взаимно перпендикулярными поляризациями. Эти два луча попадают на два фотодиода, между которыми измеряется разность генерируемого фототока. По этой разности и восстанавливается эллиптичность прошедшего оптического импульса.

Подчеркнём, что успешность измерения электрических полей этим методом напрямую зависит от того, насколько короток оптический импульс. В работе использовался импульс инфракрасного света длительностью всего 5,8 фемтосекунд (1 фемтосекунда = 10⁻¹⁵ секунды), это составило всего 1,5 периода световой волны. Этим импульсом измерялись поля с периодом от 8 до 25 фемтосекунд (длиной волны от 2,5 до 7,5 микрон).

Идея работы заключается в том, что даже в отсутствие длинноволнового излучения квантовые флуктуации электрического поля будут приводить к изменению поляризации оптического импульса, которое можно измерить и тем самым определить величину флуктуирующего электрического поля. Квантовые флуктуации, однако, носят случайный характер и проявляют себя в виде шумов. Это означает, что если повторять эксперимент много раз, то измеренное поле будет случайным образом меняться. В среднем оно будет равно нулю, но можно измерить его среднеквадратичное отклонение от нуля.

Проблема заключается в том, что квантовые флуктуации являются не единственным источником шума. Более того, есть более сильные его источники. В частности, в обсуждаемой работе намного больший вклад в шум давал так называемый дробовой шум: из-за квантовой природы света количество регистрируемых фотонов оптического импульса случайным образом меняется от выстрела к выстрелу. Оценки показывают, что в условиях обсуждаемого эксперимента дробовой шум приводил в среднем к отклонениям измеренного поля на величину около 65 В/см, в то время как квантовые флуктуации ожидалась в среднем на уровне 20 В/см.

Чтобы побороть эту проблему, в эксперименте сравнивались между собой случаи, когда присутствует только дробовой шум, и когда присутствует также и шум от квантовых флуктуаций. При этом сравнивалось среднеквадратичное отклонение измеренного поля от нулевого значения. По оценкам, разница между двумя случаями должна была составить величину всего лишь около 4,7%.

Чтобы реализовать случай, когда шум от квантовых флуктуаций отсутствует, экспериментаторы использовали увеличение размера оптического импульса на основе двух различных техник. В первой из них они удлиняли оптический импульс почти в 20 раз, до 100 фемтосекунд, а во втором — смещали электрооптический кристалл из точки фокуса так, что в месте расположения кристалла значительно возрастала ширина импульса (рис. 2). В результате в обоих подходах импульс становился значительно больше размера измеряемых флуктуаций, и суммарный вклад от них равнялся практически нулю (конечно, в вакууме присутствуют флуктуации любого размера, но можно показать, что чем больше их размер, тем меньший вклад они дадут в измеряемый сигнал).

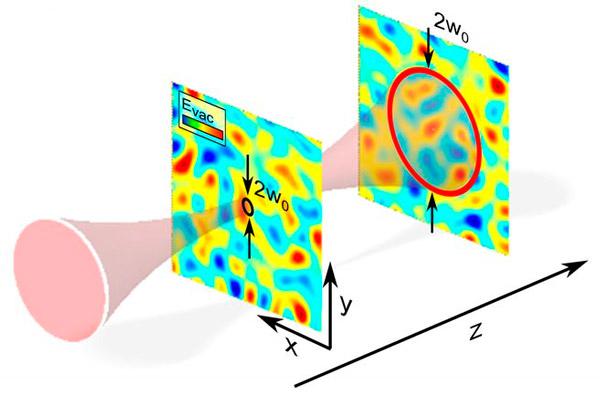Рис. 2. Иллюстрация принципа усреднения сигнала от квантовых флуктуаций при уширении пучка. Если кристалл находится в фокусе импульса, то ширина пучка мала и в него попадает приблизительно одна флуктуация. Если же кристалл отдаляется от фокуса, то ширина пучка увеличивается, и в него попадает много флуктуаций, которые друг друга компенсируют, давая в сумме практически нуль. Изображение из обсуждаемой статьи в Science

Оба метода показали, что среднеквадратичное отклонение измеренного поля от нулевого значения, действительно, уменьшается, если шум от квантовых флуктуаций удаляется, и измеренное уменьшение в обоих подходах составило величину около 4%, что достаточно хорошо совпадает с теоретическими оценками.

В заключение отметим, что, хотя результат измерений совпал для двух подходов, использованный метод не лишён недостатков, которые могут поставить корректность эксперимента под вопрос. В частности, не принимавший участия в эксперименте физик Стив Ламоро (Steve Lamoreaux) из Йельского университета отметил, что измеренные флуктуации могли быть вызваны тепловыми шумами в самом электрооптическом кристалле, в котором проводились измерения. Ламоро известен тем, что в 1997 году одним из первых с достаточно высокой точностью измерил упоминавшийся выше эффект Казимира.

Как бы то ни было, опубликованная работа должна дать толчок к новым экспериментальным попыткам измерить квантовые флуктуации напрямую. Проведённые с большей аккуратностью, они покажут, действительно ли учёные из Констанцского университета зарегистрировали квантовые флуктуации или измеренный ими сигнал имеет более прозаичное происхождение.

Источник: C. Riek et al. Direct sampling of electric-field vacuum fluctuations // Science. 2015. Published Online 1 October. DOI: 10.1126/science.aac9788.

Артем Коржиманов