
Эффекты поля нулевых колебаний вакуума
Флуктуации вакуума (nan)
ИЗЛУЧЕНИЕ ПРИ ПЕРЕХОДАХ МЕЖДУ ДИСКРЕТНЫМИ УРОВНЯМИ
Основные характеристики поля излучения в квантовой механике можно получить. исходя из аналогии с классической электродинамикой. Величина электрического и магнитного векторов волны пропорциональна экспоненте
(1) exp[i (kr – ωt )],
в аргументе которой угловая частота ω и модуль волнового вектора k связаны соотношением
ω = kс.
Возможно излучение электрического и магнитного типов, каждый их которых имеет дипольную и квадрупольную составляющие. Существуют также октупольная и более высокие типы симметрии, но первых двух в теории излучения обычно достаточно. Важную роль играет малая величина постоянной тонкой структуры a. Она обеспечивает относительно долгое время жизни возбуждённого атома по сравнению с периодом обращения электрона по классической орбите, а также доминирующий вклад излучения электрического дипольного типа.
19.1 Электрическое дипольное излучение
Рассмотрим электрический диполь, совершающий гармонические колебания. Его момент равен произведению заряда на вектор r — смещение от положения равновесия. Формулу для дипольного момента запишем сразу применительно к электронам:
так как именно они, в силу малой массы, светят ярче других частиц. Далее всюду мы будем рассматривать случай монохроматических колебаний, когда смещение определяется гармонической функцией времени:
Мощность излучения классического диполя равна
Учитывая формулы (1.1) и (1.2), получаем:
В применении к атому частота ω = ωmn определяется через энергию перехода между двумя уровнями:
В квантовой механике наряду с мощностью W принято пользоваться вероятностью перехода:
Она равна числу излучаемых за секунду квантов. Формулой (1.5) можно пользоваться только для приближённых оценок: как мы знаем, радиус орбиты r0 в квантовой механике не имеет определённого значения. Но она вполне пригодна для определения зависимости вероятности перехода от параметров системы, таких как частота перехода и заряд ядра. Ниже, в третьем разделе мы приведём точную формулу, а здесь выполним качественные оценки для атома водорода и водородоподобных ионов:
В множителе kr0 радиус орбиты r0 примем равным a0 — размеру иона или атома в теории Бора, а частоту ω выражаем через энергию перехода:
Таким образом
Для переходов оптического диапазона величина ωmn составляет около 1015 c–1, следовательно, Amn ~ 109 с–1.
Выясним зависимость Amn от заряда Z ядра водородоподобного иона. Как следует из формул (13.5.1), в случае водородоподобных ионов справедливы соотношения
(1.6) ω ~ Z2, a0 ~ 1/Z.
Согласно (1.5) вероятность переходов пропорциональна кубу частоты обращения электрона и квадрату радиуса атома:
Подставляя сюда (1.6), получим:
Таким образом, вероятность спонтанного излучения быстро растёт при переходе к многозарядным ионам.
19.2 Типы излучения при переходах между дискретными уровнями
Электрическое дипольное излучение, обозначаемое Е1, имеет место при выполнении определённых условий, Они называются правилами отбора и будут выведены ниже. В случае переходов, не удовлетворяющих правилам отбора по каналу Е1, необходимо учитывать другие, менее вероятные процессы. В астрофизических приложениях наиболее часто встречаются дипольные переходы магнитного типа М1 и электрическое квадрупольное излучение Е2.
Размеры атомов значительно меньше длины волны, то есть, величина kr значительно меньше единицы. Это позволяет разложить в ряд пространственную часть экспоненты (1)
Единица в правой части отвечает дипольному приближению. Следующие два слагаемых описывают излучение по каналам М1 и Е2. Мощность электрического квадрупольного излучения выражается через квадрупольный момент Q:
представляющий собой матрицу второго порядка:
(2.2)Индексы a и β пробегают значения 1, 2, 3, соответствующие проекциям радиус-вектора r на оси координат.
Мощность дипольного излучения магнитного типа определяется аналогично (1.3), но через вектор μ магнитного момента:
Второе равенство справа справедливо для монохроматического излучения μ ~ exp(–iωt).
Сравним вероятности электрических квадрупольных и дипольных переходов. Поскольку
d ~ er, Q ~ er2, r ~ eiωt,
то их мощности (2.1) и (1.4) относятся как
(2.4)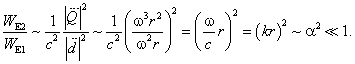
Следовательно, при одной и той же энергии кванта переход по каналу Е2 по крайней мере на четыре порядка величины менее вероятен, чем Е1:
Отметим, что малая величина произведения kr ~ a соответствует малому размеру атома r ~ a0 по сравнению с длиной волны излучаемого им света:
a0 : λ ~ a.
Теперь мы можем расширить ряд (1.3.3) пропорций, связывающих масштабы длины re, DC, и a0:
(2.5) re : DC : a0 : λ ~ a2 : a :1 :a–1.
Вероятность дипольного излучения магнитного типа также относительно невелика. Магнитный момент электрона μ по порядку величины сравним с магнетоном Бора μ0. Следовательно
(2.6)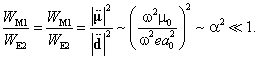
Итак, оценки (2.4) и (2.6) показали, что из трёх рассмотренных типов радиационных переходов (Е1, E2 и M1) самым интенсивным является электрическое дипольное излучение. Перейдём к описанию излучения в квантовой теории. Мы получим оценки для вероятностей переходов, а также выясним, когда следует учитывать каналы Е2 и М1.
19.3. Матричные элементы оператора дипольного излучения
Вероятность спонтанного излучения в квантовой механике отличается от (1.5) тем, что. множитель «2/3» заменяется на «4/3», а радиус–вектор электрона — на матричный элемент rmn:
Вектор
имеет три компоненты:
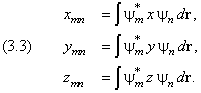
При анализе поляризованного излучения удобно использовать сферические компоненты радиус–вектора:
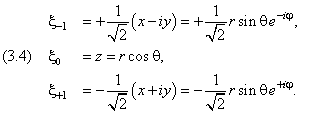
Составляющая ξ0 описывает линейно поляризованное излучение, а координаты ξ±1 — круговую поляризацию: вращение электрического вектора в двух разных направлениях.
Ниже для матричных элементов мы часто будем применять правила записи по Дираку. В них начальное и конечное состояния записываются не в поле индекса, а прямо в строке. Волновая функция ψn и её комплексное сопряжение ψ*n по Дираку обозначаются как
ψn ≡ | n >, ψ*n ≡ <n|,
а матричный элемент произвольного оператора Ĝ выглядит следующим образом:
< k |Ĝ| n > = ò ψ*k Ĝψn dr .
Запись индексов в строке удобнее в случае сложных и длинных выражений.
19.4 Ортогональность волновых функций
Важную роль в теории излучения играет ортогональность волновых функций: если квантовые состояния k и n имеют разные собственные значения энергии, то для соответствующих им волновых функций ψn и ψk справедливо равенство:
Здесь интегрирование выполняется по всему пространству, а dr, как обычно, обозначает элемент объёма. Выведем (4.1) для одномерного случая. По условию задачи, обе функции, ψk и ψn, являются решениями уравнения Шредингера с разными собственными значениями, Ek и En:
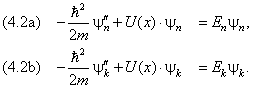
Уравнение (4.2a) умножим на ![]() , а (4.2b) сначала запишем в комплексно сопряжённой форме
, а (4.2b) сначала запишем в комплексно сопряжённой форме
после чего умножим на ψn. Вычтем второе преобразованное уравнение из первого и проинтегрируем результат по всей области изменения аргумента:
После интегрирования по частям разность двух интегралов справа приобретает вид:
Легко убедиться, что последнее выражение равно нулю: интегралы взаимно уничтожаются, а волновая функция вместе с её производной на бесконечности исчезают. Таким образом, мы приходим к равенству
из которого в силу первоначального предположения
вытекает (4.1). Ортогональность и нормировка объединяются в условие ортонормированности волновых функций связанных состояний:
Например, ортонормированными являются рассмотренные выше сферические функции (13.6.2):
![]() .
.
При различных значениях l и m они автоматически оказываются ортогональными как собственные векторы оператора квадрата момента:
По аналогичной причине ортонормированны функции Φm(φ) как собственные векторы проекции lz:
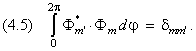
Но функции Θlm(θ) сами по себе не являются собственными функциями какого–либо из операторов момента; они взаимно–ортогональны при различных l, но не при различных m.
Условиям ортогональности и нормировки удовлетворяет также спиновая волновая функция (18.3.5). Спиновая переменная σ принимает ровно два значения, σ = ±½, поэтому в данном случае условие нормировки выражается в виде сумм
для обоих значений ms = ±½. Вычислим эти суммы:
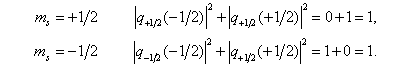
Аналогичным образом выводятся соотношения ортогональности для разных состояний — ms и ms'.
Действительно, пусть ms = –½ , а ms' = +½. Тогда:
Такой же результат получается при другой паре: ms = +½ , а ms' = –½. Два условия, (4.6) и (4.7), можно объединить в одно
аналогичное (4.3).
19.5 Правила отбора по орбитальному квантовому числу
Некоторые атомные переходы не могут осуществляться по каналу электрического дипольного излучения. Их называют запрещёнными. Космические объекты дают многочисленные примеры запрещённых переходов: небулярные, наблюдаемые в газовых туманностях, корональные — в звёздных спектрах, а также линия λ=21 см нейтрального водорода. В этом разделе мы изложим способ выявления разрешённых и запрещённых переходов применительно к водородоподобным системам. Существуют правила отбора, на основании которых делают вывод о том, возможен ли данный переход как электрически дипольный, или же надо искать другие типы излучения.
На примере линейно поляризованного излучения покажем, как могут быть получены правила отбора для водородоподобной системы, точнее — для электрона, находящегося в кулоновском поле. Для решения этой задачи достаточно выяснить, при каких параметрах перехода матричный элемент радиус–вектора оказывается равным нулю. Даже такая, на вид несложная задача, требует определённой математической подготовки.
Когда матричный элемент отличен от нуля?
Правила отбора полностью определяются зависимостью волновых функций от угловых переменных. Ниже нам потребуется формула, связывающая присоединённые полиномы Лежандра с тремя последовательными значениями нижнего индекса: ![]() ,
, ![]() , и
, и ![]() . Приведём её без вывода:
. Приведём её без вывода:
где
Вероятность линейно поляризованного излучения пропорциональна квадрату модуля матричноого элемента <k|z|n>, угловая часть которого содержит интеграл
Для упрощения записи формул здесь и в дальнейших выкладках этого параграфа мы опускаем индекс m у сферических функций — сейчас он не играет никакой роли. Согласно (4.1), последний интеграл равен
Учитывая условие (4.4) ортонормированности сферических функций, окончательно получаем:
Теперь очевидно, что матричный элемент отличен от нуля только в том случае, если l' отличается от l на единицу в ту или иную сторону. Аналогично вычисляется вероятность излучения, поляризованного по кругу, только в подынтегральной функции, согласно (3.4), надо заменить произведение ![]() Опуская математические выкладки, сообщим, что результат остаётся тем же самым, что и для линейной поляризации.
Опуская математические выкладки, сообщим, что результат остаётся тем же самым, что и для линейной поляризации.
Итак, сформулируем правило отбора по орбитальному квантовому числу l для атома водорода или водородоподобного иона в кулоновском приближении: вероятность электрического дипольного излучения отлична от нуля при выполнении условия
Дальше мы увидим, что это правило сохраняется и при переходе к более сложным системам. Оно остаётся справедливым для одноэлектронных переходов в поле с центральной симметрией.
Схема переходов без учёта тонкой структуры
Схемы переходов того или ионного иона или атома называются диаграммой Гротриана. Такие схемы, по существу, мы уже приводили в четырнадцатой главе. Рисунки 14.1.1 и 14.3.1 используют максимально упрощённую модель, в которой энергия любого состояния атома водорода полностью определяется величиной главного квантового числа. Такое упрощение вполне приемлемо, пока мы не интересуемся типом излучаемого кванта.
Теперь мы перейдём к рассмотрению только разрешённых переходов, то есть, излучения по каналу d1. Усложнение модели проведём в два этапа. Сначала учтём орбитальное квантовое число l, но временно не будем учитывать тонкую структуру. Диаграмма Гротриана для первых четырёх уровней атома водорода приведена на рис.19.5.1
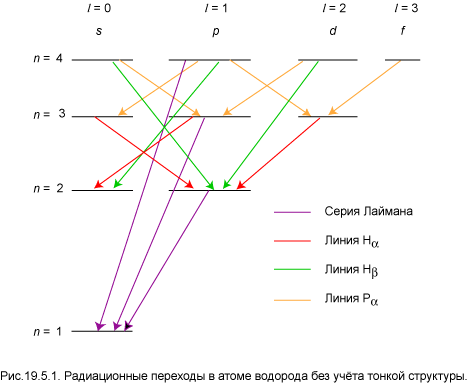
Серия Лаймана в этом приближении состоит из одиночных линий,
np → 1s, n … 2,
и учёт орбитального квантового числа не приносит ничего нового по сравнению с рис.14.1.1. Переходы остальных серий содержат несколько компонент. В серии Бальмера три компоненты:
np → 2s,
ns, nd → 2p, n … 3
и её схема усложнилась по сравнению с рис.14.3.1. В серии Пашена уже пять компонент:
np → 3s,
ns, nd → 3p, n … 4
np, nf → 3d,
а в общем случае их число равно 2n–1, где n — главное квантовое число нижнего уровня. В кулоновском приближении все компоненты в сумме дают одну линию.
19.6. Правила отбора по полному моменту
Спин–орбитальное взаимодействие приводит к тому, что орбитальный момент hl перестаёт быть сохраняющейся величиной, и формула (4.3), строго говоря, становится приближённой. Интегралом движения остаётся полный момент атома ћj, условием сохранения которого является только отсутствие внешних полей. Поэтому в случае изолированного атома действует точное правило отбора по квантовому числу j. Его мы определяем из следующих соображений.
Дипольное излучение
Из квантовой электродинамики известно, что каждому каналу излучения соответствует своё значение внутреннего момента фотона hQ. Так, в случае дипольного излучения величина Q равна единице:
(6.1) QE1, M1 = 1.
Допустимые изменения момента
Δj = j΄ – j
определяются уже известным нам правилом сложения векторов. Пусть в результате поглощения кванта момент атома изменяется с j на j΄. Из закона сохранения момента вытекает:
(6.2) j΄ = j + Q.
Проекция момента Qz может принимать три значения:
(6.3) Qz = –1, 0, +1.
Как и в предыдущем разделе, полезно рассмотреть два варианта: j < 1 и j … 1. В первом случае, согласно (12.2), j равно нулю, либо половине.
Конечно, полный момент одного электрона не может быть равен нулю. Поэтому в случае атома водорода или водородоподобного иона можно было бы начинать сразу со случая j = ½ . Но рассматриваемое здесь правило отбора по полному моменту имеет общий характер: оно применимо ко всем ионам и атомам. Здесь важно только отсутствие внешнего поля. Внутренний момент системы из нескольких электронов уже может оказаться равным нулю, поэтому мы обсудим все возможные варианты.
- j = 0. В этом случае jz принимает единственно возможное — нулевое значение, и полный набор проекций j΄z совпадает с (6.3). Следовательно, j΄ = 1 и
(6.4a) j΄ = j+1.
- j = ½. Задача с сочетанием моментов 1 и ½ в другом контексте уже была решена в разделе (18.4). Мы можем воспользоваться формулой (18.4.5), заменив в ней j на j΄ и l на j. В результате получим
(6.4b) j΄ = 1/2, 3/2.
- j … 1. По аналогии с разделом 18.4, все 3*(2j+1) значения пар проекций Qz и jz запишем в таблицу с тремя строками и 2j+1 столбцами.
Таблица 19.6.1 Случай j… 1
–j – 1 | –j | –j +1 | –j + 2 | … | j – 4 | j – 3 | j – 2 | j – 1 |
–j | –j +1 | –j + 2 | –j + 3 | … | j – 3 | j – 2 | j – 1 | j |
–j +1 | –j + 2 | –j + 3 | –j + 4 | … | j – 2 | j – 1 | j | j + 1 |
Первая строка отвечает значению Qz, равному «–1» из (6.3), вторая — нулю, третья — «+1». Красным цветом помечены 2j+3 = 2*(j+1)+1 проекции, отвечающие полному моменту j΄, равному j+1. Зелёный ряд — 2j+1 проекция момента j, а чёрный — 2j–1 = 2(j–1)+1 проекция момента j–1. Итак, j΄ может принять три значения:
(6.4c) j΄ = j–1, j, j+1.
Все три формулы (6.4a,b,c) можно объединить следующим образом:
(6.5a) Δj = 0, ±1,
(6.5b) j + j΄ … 1.
Полученный результат напоминает (5.3), но между ними есть и серьёзное различие. Орбитальный момент обязан измениться, а полный момент, если он отличен от нуля, может сохранить своё прежнее значение. Противоречия здесь нет. Дело в том, что существуют ещё правила отбора по чётности. Они формулируются отдельно от правил отбора по моменту, но формула (4.3) учитывает их автоматически.
В этом пункте мы не различали два канала дипольного излучения. Действительно, фотоны E1 и М1 имеют одно и то же значение момента, равное ћ, следовательно, их свойства по отношению к правилу отбора по моменту одинаковы. Но различие между ними, конечно, существует. Оно связано с дополнительными запретами излучения по каналу М1 и будет рассмотрено позднее.
Квадрупольное излучение
Внутренний момент фотона, излучаемого или поглощаемого по каналу Е2, равен 2ћ:
(6.6) QE2 = 2
Дальнейшие рассуждения во многом аналогичны случаю дипольного излучения и новым в них является только численное значение момента фотона. Проекция момента Qz теперь может принимать пять значений:
(6.7) Qz = –2, –1, 0, +1, +2.
Следовательно, надо рассмотреть два варианта: j … 2 и j < 2. Для первого варианта справедлива таблица 19.6.2
Таблица 19.6.2 Случай j … 2
–j – 2 | –j–1 | –j | –j + 1 | … | j – 6 | j – 5 | j – 4 | j – 3 | j – 2 |
–j – 1 | –j | –j +1 | –j + 2 | … | j – 5 | j – 4 | j – 3 | j – 2 | j – 1 |
–j | –j +1 | –j + 2 | –j + 3 | … | j – 4 | j – 3 | j – 2 | j – 1 | j |
–j + 1 | –j + 2 | –j + 3 | –j + 4 | … | j – 3 | j – 2 | j – 1 | j | j + 1 |
–j + 2 | –j + 3 | –j + 4 | –j + 5 | … | j – 2 | j – 1 | j | j + 1 | j + 2 |
Она составлена аналогично таблице 19.6.1, но имеет пять строк, по числу проекций внутреннего момента фотона. Хорошо видно, что пять цветных рядов проекций отвечают пяти возможным значениям момента j':
Красный | Синий | Зелёный | Оранжевый | Чёрный |
j' = j + 2 | j '= j + 1 | j' = j | j' = j – 1 | j' = j – 2 |
Ясно, что вместо правила (6.5а) мы получаем условие
(6.8a) Δj = 0, ±1, ±2.
Из четырёх возможных значений квантового числа j, меньших двойки: 0, ½, 1, 3/2 для первых трёх результаты были получены в предыдущем пункте. Построим таблицу проекций для пары моментов Q = 2 и j =3/2. В левом столбце приведены все проекции момента фотона, а в верхней строке — проекции j.
Таблица 19.6.2 Случай Q=2, j.= 3/2
mj Qz | 3/2 | 1/2 | –1/2 | –3/2 |
2 | +7/2 | +5/2 | +3/2 | +1/2 |
1 | +5/2 | +3/2 | +1/2 | –1/2 |
0 | +3/2 | +1/2 | –1/2 | –3/2 |
–1 | +1/2 | –1/2 | –3/2 | –5/2 |
–2 | –1/2 | –3/2 | –5/2 | –7/2 |
Очевидно, что здесь j' может принимать четыре значения:
j' = 1/2, 3/2, 5/2, 7/2.
Последний результат в совокупности с (6.4a,b) можно обобщить следующим образом:
(6.8b) j + j' … 2.
Формулы (6.8а,b) исчерпывают правила отбора по моменту для квадрупольного излучения.
19.7 Правила отбора по чётности
Пусть обе волновые функции в (3.2) имеют одинаковую четность. Иными словами, либо они одновременно меняют свой знак при воздействии на них оператора инверсии r → –r, либо обе сохраняют своё значение. Покажем, что в этом случае матричный элемент дипольного момента равен нулю. Для этого выполним замену переменных
(7.1) ρ = –r.
Численное значение результата не зависит от выбора переменных интегрирования. Но после замены (6.1) матричный элемент меняет знак:
![]() ,
,
что возможно только при rmn = 0. Поясним эту цепочку равенств. Произведение волновых функций не меняет знака в силу сделанного предположения об их одинаковой чётности. Кроме того, области интегрирования по r и по ρ одинаковы, а также равны элементы интегрирования dr =dρ = dx·dy·dz. Таким образом, в случае электрического дипольного излучения запрещены переходы между состояниями с одинаковой чётностью. Это даёт дополнительное правило отбора, которое мы запишем символически:
(7.3) чётное € нечётное для дипольного излучения электрического типа.
Теперь становится ясен смысл запрета на изменение орбитального квантового числа l: согласно (12.7.6), он отражает правило отбора по чётности. Переходы с Δj = 0 не запрещены, так как полный момент не связан непосредственно с чётностью.
В случае каналов М1 и Е2 также имеют место правила отбора по чётности, но они прямо противоположны (6.3). Причина отличия заключается в следующем. Магнитный момент m является аксиальным вектором, а не полярным, как дипольный момент d. Поэтому в отличие от d он не меняет знака при операции инверсии:
(7.4) m(–r) = m(r).
Матрица квадрупольного момента (2.2) содержит парные произведения координат; поэтому она также не меняет знака:
(7.5) Qab(–r) = Qab(r).
Из (7.4) и (7.5) вытекает правило отбора по чётности для каналов Е2 и М1:
(7.6) чётное € чётное и нечётно € нечётное.
Действительно, здесь можно буквально повторить все рассуждения, которые нас привели к (6.2). Только теперь знак «минус» во втором равенстве (7.2) появится, если произведение волновых функций изменит свой знак при операции инверсии. Иными словами, матричные элементы mmn и Qmn равны нулю в случае волновых функций разной чётности.
19.8 Мультиплеты атома водорода
Мультиплетом называется совокупность линий, образованных переходами между компонентами тонкой структуры уровней nl и n΄l΄, то есть разрешённые переходы
nlj → n΄l΄j΄.
С учётом тонкой структуры серия Лаймана расщепляется на две линии:
1s1/2 → np1/2, 1s1/2 → np3/2.
Её дублетная структура иллюстрируется рис. 19.8.1. Пунктиром условно помечены положения
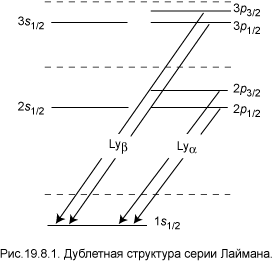
уровней в кулоновском приближении. Для удобства восприятия значительно увеличен масштаб тонкой структуры.
Отметим интересное свойство уровня 2s1/2: с него нет пути вниз по каналу электрического дипольного излучения. Такие уровни называются метастабильными. Длительное пребывание атома в метастабильных состояниях делает возможным их относительно большую населённость.
В случае бальмеровской серии разрешены 7 переходов:
2s1/2 → np1/2, 2p1/2 → ns1/2, 2p1/2 → nd3/2,
2p3/2 → nd3/2,
2s1/2 → np3/2, 2p3/2 → ns1/2, 2p3/2 → nd5/2.
Схема переходов для линий Ha приводится на рис.19.8.2. Вследствие того, что уровни ns1/2 и np1/2, np3/2 и nd3/2 попарно совпадают, каждая из линий серии Бальмера состоит из пяти компонент. Компоненты
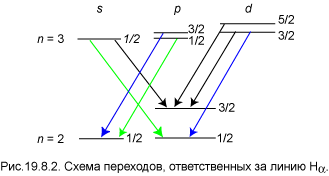
таких пар обозначены на рисунке одинаковым цветом — синим или зелёным.
В общем случае переходов на нижний уровень с главным квантовым числом n получается равным
(8.1) Ntrans = 6n–5.
Их число легко сосчитать, воспользовавшись схемой на рис. 19.8.3.
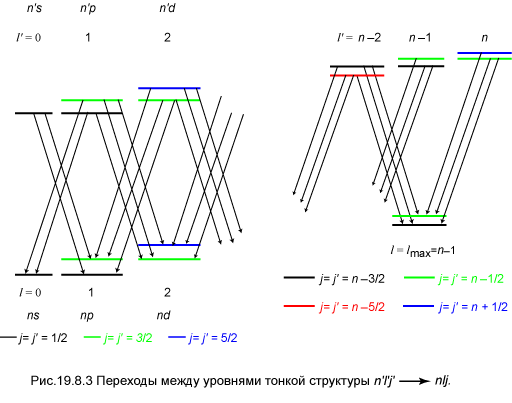
Число компонент линии n’ → n, имеющих разные длины волн Nline, можно подсчитать, объединив уровни с одинаковыми значениями j. По правилу отбора (6.5а) на уровень j = 1/2 возможны два перехода, а на все остальные — по три. Квантовое число полного момента при заданном значении n может принимать n разных значений, от 1/2 до n – 1/2. Следовательно, Nline равно
(8.2) Nline = 2 + 3(n – 1) = 3n – 1.
Наглядное представление о числе компонент можно получить из рис. 19.8.4.
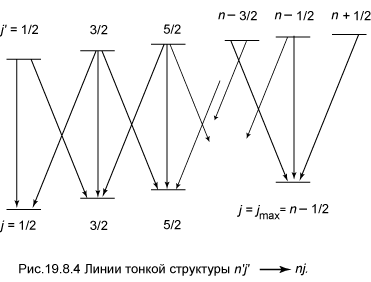
Значения Ntrans и Nline для первых пяти серий атома водорода и водородоподобных ионов, вычисленные по формулам (8.1) и (8.2), приведены в табл. 19.8.1.
Таблица 18.8.1 Число переходов и число линий тонкой структуры
Серия | n | Ntrans | Nline |
Лаймана | 1 | 2 | 2 |
Бальмера | 2 | 7 | 5 |
Пашена | 3 | 13 | 8 |
Брекета | 4 | 19 | 11 |
Пфунда | 5 | 25 | 14 |
Обе величины в силу правил отбора полностью определяются значением главного квантового числа нижнего состояния. Поэтому они одинаковы для всех членов определённой серии.
В условиях звёздных атмосфер или межзвёздного газа отдельные компоненты тонкой структуры атома водорода, как правило, не видны. Они перекрываются за счёт конечной ширины линий, обусловленной либо доплеровскими смещениями, либо эффектами давления. Но резонансные переходы водородоподобных ионов железа уже имеют достаточно высокую величину расщепления и отдельные компоненты тонкой структуры могут наблюдаться в спектре солнечной короны.
19.9 Взаимодействие электронов с полем нулевых колебаний
В конце 40-х гг. развитие высокочастотной техники позволило физикам исследовать структуру уровней атома водорода с n=2. В результате было обнаружено взаимодействие атомного электрона с полем нулевых колебаний, о котором шла речь в главе 11. Это взаимодействие проявляется в нескольких аспектах. Здесь мы изложим результаты опытов Лэмба–Ризерфорда по расщеплению состояний атома водорода с одной и той же величиной j, но разными значениями l. Принципиальное значение для развития квантовой электродинамики имело обнаружение так называемого аномального магнитного момента электрона — его отличия от магнетона Бора. Поле нулевых колебаний определяет также силы Ван дер Ваальса при взаимодействии двух молекул в s–состояниях. Также будет рассмотрен эффект Казимира.
Опыты Лэмба–Ризерфорда
Учёт релятивистских эффектов — зависимости массы электрона от скорости и спин–орбитального взаимодействия — привели нас к формуле (18.8.3). Поправка к энергии уровня с главным квантовым числом n определяется полным моментом j и не зависит от величины l (рис.18.8.1). Оставшееся вырождение по квантовому числу l снимается за счёт взаимодействия атомного электрона с электромагнитным полем нулевых колебаний, природа которых изложена в главе 11. Нулевые колебания, или колебания вакуума, приводят к положительному смещению уровня 2 2s½ относительно уровня 2 2p. Это смещение было замечено ещё в 1934 г., но первые точные измерения были проведены в 1947 г. Лэмбом и Ризерфордом радиоскопическим методом.
Схема опыта приведена на рис. 19.9.1. В вакуумном сосуде находилась вольфрамовая печь 1,
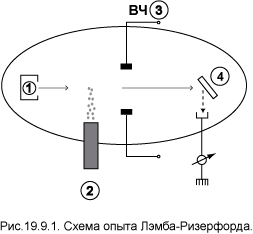
создающая пучок атомов водорода в основном состоянии 12s1/2. Пучок, нагретый печью до температуры около 2·103К ≈ 0.2 эВ, направлялся на электрод 4, способный эмитировать электроны, если его бомбардируют частицы, энергия которых превышает работу выхода. В эксперименте использовался образец с работой выхода несколько электронвольт, поэтому кинетическая энергия атомов была недостаточной для выбивания из него электронов. Но пушка 2 испускала электроны, достаточно энергичные для возбуждения атома водорода на высокие уровни. В дальнейшем, после каскада спонтанных переходов, атомы, большей частью, оказывались в основном состоянии. Но на метастабильном уровне 22s1/2 имеет место накопление атомов. Энергия возбуждения второго уровня — 10.2 эВ — вполне достаточна для преодоления работы выхода из вещества электрода. На электрод 4 попадает пучок возбуждённых атомов и выбивает из него электроны, генерируя в цепи электрический ток.
Величину энергетической щели между близкими уровнями позволяет измерить источник высокочастотного излучения 3. Например, если его частота равна частоте перехода 22s1/2 → 22p3/2, то атомы водорода под воздействием излучения переходят с метастабильного состояния на уровень 22p3/2, с которого уже возможен разрешённый радиационный переход в основное состояние. Распад состояния 22p3/2 происходит примерно за 10–9 с, что значительно меньше времени пролёта от печи до мишени. Итак, в случае резонанса произойдет цепочка переходов
22s1/2 → 22p3/2 → 12s1/2.
На электрод попадут атомы только в основном состоянии, их энергия весьма мала, и тока не будет.
Частота излучения, соответствующая переходу 22s1/2 → 22p3/2 , лежит в диапазоне 104 МГц, и соответствующее прекращение тока было обнаружено. Но в опытах Лэмба и Ризерфорда ток исчезал еще при одной частоте ВЧ–источника, равной (1062±5) Мгц. Это означает, что существует разница энергий между уровнями 2s1/2 и 2p1/2, и возможна другая цепочка переходов в основное состояние:
2s1/2 → 2p1/2 → 1s1/2.
Таким образом, энергия уровня с n = 2 и j = ½ зависит от величины орбитального квантового числа l. Схематически это изображено на рис.19.9.2.
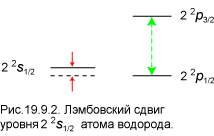
Зелёная стрелка справа на рисунке обозначает уже известное нам расщепление уровней с разными значениями j, оно определяется спин–орбитальным взаимодействием и зависимостью массы электрона от скорости. Двумя красными стрелками отмечена разность энергий s и p состояний при одном и том же значении j. Она получила название лэмбовского сдвига.
Лэмбовский сдвиг
В основе теории лэмбовского сдвига лежит понятие физического вакуума — низшего энергетического состояния квантованных полей, характеризующегося отсутствием каких–либо реальных частиц. Частицы как бы пребывают в виртуальном состоянии. Нулевые колебания вакуума проявляются только при взаимодействии с реальными частицами. Например, спонтанное излучение можно интерпретировать как превращение виртуального фотона в реальный квант света при переходе возбуждённого атома в основное состояние. И наоборот, поглощение излучения означает переход фотона в виртуальное состояние. Существует также электрон–позитронный вакуум, откуда возникают реальные частицы при рождении электрон–позитронных пар. Обратный процесс — аннигиляция электрона и позитрона соответствует их переходу в виртуальное состояние. Теоретическое обоснование лэмбовского сдвига в 1949 г. дал Бёте. Мы остановимся на упрощённом рассмотрении эффекта, ограничившись вкладом нулевых колебаний электромагнитного поля.
Электромагнитному вакууму соответствует нулевая энергия осцилляторов (11.1.10). Напомним выведенную в одиннадцатой главе формулу (11.1.9) для энергии гармонического осциллятора равна
En = ħ ω(n+½).
В основном состоянии при n = 0 имеют место вакуумные, или нулевые колебания. Они приведены на рис.11.2.1.
Колебания электромагнитного вакуума имеют хаотический характер, поэтому средняя напряжённость их электрического поля равна нулю. Но средний квадрат амплитуды напряженности поля отличен от нуля и именно с этим обстоятельством связан лэмбовский сдвиг. На рис. 19.9.3 изображены электрон e– и ядро Ze. Здесь r обозначает радиус–вектор электрона без учёта его движения под влиянием нулевых колебаний. Колебания вакуума вызывают «дрожания» электрона, которые
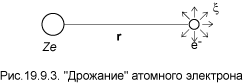
описываются вектором ξ. Эти дополнительные перемещения значительно меньше расстояния до ядра:
(9.1) ξ = r.
Так как электрон находится в поле ядра, то его дополнительные перемещения вызывают изменения кулоновского потенциала φ. В силу (9.1) изменение потенциала относительно невелико, и мы можем применить разложение в ряд Тейлора по малому параметру ξ. Введём обозначения x1, x2, x3 для координат xyz радиус–вектора r. Аналогичным образом обозначим компоненты ξ1, ξ2, ξ3 смещения ξ. Тогда
(9.2) φ(r+ξ) – φ(r) = ξi ∂φ/∂xi + ½ξiξj ∂²φ/∂xi ∂xj + …
Здесь по повторяющимся индексам выполняется суммирование. Усредним изменение потенциала по угловым переменным, учитывая хаотичный характер «дрожания» электрона. Хаотичность означает, что в среднем электрон не меняет своего положения
(9.3a) <ξi> = 0,
смещения по разным направлениям статистически независимы,
(9.3b) < ξi·ξj > = <ξi >·<ξj > = 0
и их средние значения одинаковы:
(9.3c) < ξ2x > = < ξ2y > = < ξ2z >.
Три формулы (9.3a,b,c) имеют компактную форму записи:
(9.4) <ξi·ξj> = ⅓<ξ2>δij,
где
<ξ2> = < ξ2x > + < ξ2y > + < ξ2z >.
С помощью (9.2) и (9.4) получим:
Сумма в правой части (9.5) является оператором Лапласа. Поэтому с помощью уравнения Пуассона
её можно выразить через плотность ρ зарядов, создающих поле с потенциалом φ. В данном случае поле создаётся ядром. Поэтому весь заряд, определяющий электростатический потенциал, сосредоточен в начале координат:
Энергия электрона в поле с потенциалом φ равна
(9.8) U = –eφ.
Подставим (9.7) и (9.6) в (9.5) и с помощью (9.8) получим выражение для среднего значения изменения энергии электрона:
Величину <ξ2> найдём из уравнения движения электрона в поле нулевых колебаний.
(9.10)Здесь E — напряжённость электрического поля электромагнитного вакуума. Перепишем последнее уравнение для Фурье–компонент смещения и поля:
(9.11)где ωk — частоты мод колебаний. Для Фурье–компонент уравнение (9.10) превращается в алгебраическое с простым решением:
(9.12)Теперь найдём Фурье–компоненты поля волны. Посредством ΔNk обозначим число колебаний в узком интервале волновых чисел от k до k + Δk. Оно совпадает с числом колебаний ΔNω в интервале частот от ω до ω + Δω, если частота и волновое число связаны известным дисперсионным уравнением ω = kc. Тогда из (2.2.8) следует
Внутри диапазона волновых чисел Δk сосредоточена энергия колебаний поля, равная
(9.13) Ek = ½ ħωkΔNk
С другой стороны, эта же энергия определяется Фурье–компонентой напряжённости поля:
(9.14)Приравняв друг другу левые части (9.13) и (9.14), получим:
(9.15)откуда, согласно (9.12), следует выражение для среднего значения квадрата смещения:
(9.16)
Просуммируем (9.16) по модам колебаний:
Заменим суммирование интегрированием и вычислим определённый интеграл с нижним пределом ω1 и верхним ω2:
(9.17)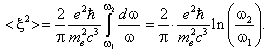
Полученный интеграл имеет логарифмическую расходимость на нижнем и верхнем пределах. Нижний предел ω1 выберем из условия резонанса электрона и волны:
(9.18) ћω1 = 2·Z2 Ry.
Действительно, рассматриваемая модель предполагает, что можно пренебречь скоростью движения электрона в кулоновском поле ядра по сравнению со скоростью его «вибрации» в поле нулевых колебаний. Это предположение не выполняется для колебаний, частота которых меньше частоты обращения электрона по орбите ~ Z2 Ry/ћ. Выбор множителя «2» в правой части (9.18) обсудим ниже.
Вибрация релятивистского электрона значительно ослаблена вследствие значительного увеличения его массы. Поэтому верхнюю границу частоты ω2 можно выразить через энергию покоя электрона:
(9.19) ћω2 = mec2 = Ry/a2.
Подставив (9.18) и (9.19) в (9.17), получим:
(9.20)
В результате выбора множителя «2» в формуле (9.18) аргумент логарифма в (9.20) совпал с результатом точного расчёта, выполненного Бёте по рецептам квантовой электродинамики. Отметим, что ошибка в два–три раза при вычислении отношения ω2/ω1 не меняет существенно величины логарифма. Конечно, это справедливо только до тех пор, пока это отношение достаточно велико. Например, в случае атома водорода (Z=1) оно превосходит 104. Поэтому увеличение аргумента в два раза приводит к изменению логарифма всего на 6%.
С точностью до множителя 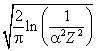 численное значение <ξ2>½ — размера области, занятой «дрожащим» электроном, есть среднее геометрическое классического радиуса электрона и его комптоновской длины волны:
численное значение <ξ2>½ — размера области, занятой «дрожащим» электроном, есть среднее геометрическое классического радиуса электрона и его комптоновской длины волны:
Теперь мы можем расширить пропорцию (2.5), связывающую друг с другом характерные масштабы re, DC , a0, λ, дополнив её новым звеном:
(9.22) re : <ξ2>½ : DC : a0 : λ ~ a2 : a3/2 : a : 1 : a–1.
Подставив (9.20) в (9.9), получим поправку к потенциальной энергии электрона:
Поправка энергетического уровня ΔELnl получается путём усреднения (9.16) по состояниям электрона.
Вспоминая свойство δ–функции:
после интегрирования (9.24) получим:
Согласно разделу 16.6, волновая функция электрона, находящегося в кулоновском поле, в начале координат отлична от нуля только для s-состояний. Из (12.6.7), (16.6.21) и (16.6.32) следует
1 Z3
|ψn(0)|2 = |Y00(θ,φ)|2·|R00(0)|2 = −−− (4Z3/n3a0) = −−−−−−−− .
4π πn3a0
В рассматриваемом приближении сдвиги уровней с l…1 равны нулю. Окончательно получим:
Приведём для справки более точное выражение, которое получается в квантовой электродинамике:
Коэффициенты Bn приведены в таблице.
n | 1 | 2 | 3 | 4 | ∞ |
Bn | 2.984 | 2.812 | 2.768 | 2.750 | 2.721 |
Современный уровень развития квантовой электродинамики позволяет с большой точностью рассчитать сдвиги уровней. Так, теоретическое значение частоты перехода 22s½ → 22p½
Δνтеор. = 1057.87(2) МГц
лишь в шестом знаке отличается от результата измерения:
Δνэксп.. = 1057.86(2) МГц.
Лэмбовский сдвиг, как и все релятивистские поправки, значительно увеличиваются у высокозарядных ионов. Причём здесь наблюдается своеобразная конкуренция нескольких процессов. Для водородоподобных ионов неона (Z=10) и цинка (Z=30) она демонстрируется в следующей таблице. В первой строке приведён заряд ядра (Z=1 для атома водорода), во второй — величина тонкой структуры (18.8.3) для 2p–электрона, в третьей — лэмбовский сдвиг состояния 2s½ относительно 2p½. Энергия расщепления измерена в электронвольтах.
Z | 1 (Водород) | 2 (Неон) | 30 (Цинк) |
ΔE(22p3/2 – 22p½ ) | 4.56·10–5 | 0.456 | 36.9 |
ΔE(22s½ – 22p½ ) | 4.38·10–6 | 0.0202 | 0.962 |
Отношение | ~ 10 | ~ 20 | ~ 40 |
Числа в четвёртой строке равны отношению величины тонкой структуры и лэмбовского сдвига для каждого иона или атома. Выражение для лэмбовского сдвига содержит кубическую зависимость от a, а не квадратичную, как тонкая структура. Однако, за счет логарифмического множителя разница в энергиях расщепления получилась всего один порядок величины, а не два, как можно было ожидать.
Аномальный магнитный момент электрона
Эффекты, связанные с полем виртуальных частиц и, в частности, с нулевыми колебаниями, проявляются в аномальном магнитном моменте электрона.
В 1947 г. Раби путём радиоспектроскопических исследований установил, что собственный магнитный момент электрона отличается от магнетона Бора. Поправку к магнитному моменту впервые получил Швингер:
Учёт членов следующего порядка малости по параметру a даёт более точное выражение:
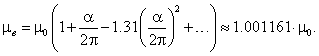
Хотя эта поправка составляет всего 0.1%, тем не менее, она наблюдалась в зеемановских спектрах атомов натрия и галлия.
Силы Ван дер Вальса
В классической механике отсутствует взаимодействие между осцилляторами при отсутствии колебаний. В действительности две молекулы могут взаимодействовать друг с другом, даже находясь в невозбуждённом состоянии. Это взаимодействие осуществляется посредством нулевых колебаний и является основанием для анализа сил Ван дер Ваальса в квантовой теории.
Эффект Казимира
Поместим в резервуар на две металлические пластины площадью S каждая и откачаем из него воздух. Расстояние d между пластинами будем считать небольшим: d = S½. В вакууме пластины притягиваются друг к другу с силой, пропорциональной отношению
F ~ S/d.
Объяснение этого эффекта состоит в том, что в пространстве между пластинами, как в волноводе или резонаторе, реализуются не все моды колебаний электромагнитного вакуума. Согласно (9.13), плотность энергии колебаний, а, следовательно, и давление между пластинами меньше, чем снаружи, и пластины притягиваются. Этот небольшой по величине эффект наблюдался экспериментально.
Теоретически возможен обратный эффект Казимира: при вынужденном колебании пластин должно появиться излучение на частоте колебаний. Но так как механическим путём пока не удаётся высоких частот, характерных для излучения в радиодиапазоне, то такой эксперимент ещё не был проведён.
19.10 Излучение нейтрального водорода на длине волны λ = 21 см
Вернёмся к вопросу о сверхтонкой структуре атома водорода. Ранее он был рассмотрен в разделе 18.9 предыдущей главы. Напомним, что взаимодействие полного момента электрона j и внутреннего момента ядра I приводит к расщеплению основного состояния атома водорода 12S1/2 на два подуровня. Квантовое число полного момента F верхнего состояния равно единице, а нижнего — нулю:
Вычислим вероятность спонтанного перехода между компонентами сверхтонкой структуры. Этот переход возможен только по каналу магнитного дипольного излучения. Действительно, электрический дипольный переход запрещён правилом отбора по чётности (5.3), а квадрупольный — правилом отбора по моменту (6.8b). Поделив мощность излучения (2.3) на энергию кванта, получим формулу для вероятности перехода
Магнитный момент электрона в атоме по порядку величины близок к магнетону Бора μ0. Для оценки численного значения AM1 подставим в (10.1) μ0 вместо |μ|. В результате получим:
A21 см ≈ 3·10–15 с–1.
Наша грубая оценка оказалась весьма близкой к точному значению вероятности перехода
A21 см = 2.85·10–15 с–1.
Эта величина мала не только для земных лабораторий, но и для космических масштабов. Например, время жизни на возбуждённом уровне F=1 составляет
τ ≈ 1/A ≈ 107 лет,
что всего в десять раз меньше времени обращения нашей Галактики вокруг центра. Но большая чувствительность радиотелескопов позволяет зарегистрировать даже такое, на первый взгляд, слабое излучение.
0Источник:
Дата создания: 07.08.2008
Последнее редактирование: 07.08.2008
Относится к аксиоматике: Флуктуации вакуума.
Другие страницы раздела "Нулевые колебания вакуума":
Чтобы оставить комментарии нужно авторизоваться: Авторизация пользователя