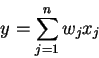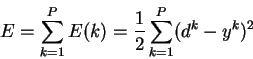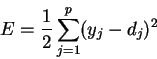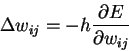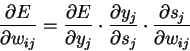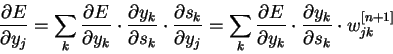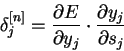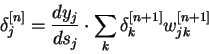Нейронные сети : обучение с учителем
Нейронные сети : обучение с учителем
Выделения в тексте - мои.<br>Мои коммнтарии включены синим цветом.
http://mechanoid.narod.ru/nns/teacher/
Е.С.Борисов
27 октября 2002 г.
1 Обучение с учителем
- Технология обучения с учителем НС предполагает наличие двух однотипных множеств:
- множество
учебных примеров
- используется для ''настройки'' НС - множество
контрольных примеров
- используется для оценки качества работы НС
Элементами
этих двух множеств есть пары ![]() , где
, где
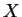 -
входной вектор для обучаемой НС;
-
входной вектор для обучаемой НС; 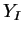 -
верный (желаемый) выходной вектор для
-
верный (желаемый) выходной вектор для 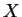 ;
; - Так же
определим функцию ошибки
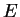 . Обычно это средняя квадратичная
ошибка (mean squared error - MSE) [6]
. Обычно это средняя квадратичная
ошибка (mean squared error - MSE) [6]
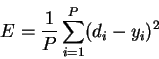
где
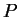 -
количество обработанных НС примеров;
-
количество обработанных НС примеров; 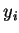 -
реальный выход НС;
-
реальный выход НС; 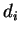 -
желаемый (идеальный) выход НС;
-
желаемый (идеальный) выход НС; - Процедура
обучения НС сводится к процедуре коррекции весов связей HC. Целью
процедуры коррекции весов есть минимизация функции ошибки
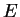 .
.
- Общая схема обучения с учителем выглядит так :
1. Перед началом обучения весовые коэффициенты НС устанавливаются некоторым образом, на пример - случайно.
2.
На первом этапе
на вход НС в определенном порядке подаются учебные примеры. На каждой
итерации вычисляется ошибка для учебного примера ![]() (ошибка обучения) и по
определенному алгоритму производится коррекция весов НС. Целью процедуры коррекции
весов есть минимизация ошибки
(ошибка обучения) и по
определенному алгоритму производится коррекция весов НС. Целью процедуры коррекции
весов есть минимизация ошибки ![]() .
.
3.
На втором этапе
обучения производится проверка правильности работы НС. На вход НС в
определенном порядке подаются контрольные примеры. На каждой итерации
вычисляется ошибка для контрольного примера ![]() (ошибка обобщения). Если результат
неудовлетворительный то, производится модификация множества учебных примеров1
и повторение цикла обучения НС.
(ошибка обобщения). Если результат
неудовлетворительный то, производится модификация множества учебных примеров1
и повторение цикла обучения НС.
- Если
после нескольких итераций алгоритма обучения ошибка обучения
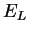 падает
почти до нуля, в то время как ошибка обобщения
падает
почти до нуля, в то время как ошибка обобщения 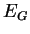 в начале спадает а
затем начинает расти, то это признак эффекта переобучения. В этом
случае обучение необходимо прекратить.
в начале спадает а
затем начинает расти, то это признак эффекта переобучения. В этом
случае обучение необходимо прекратить.
В случае однослойной сети алгоритм обучения с учителем - прост. Желаемые выходные значения нейронов единственного слоя заведомо известны, и подстройка весов синаптических связей идет в направлении, минимизирующем ошибку на выходе сети.
По этому принципу строится алгоритм обучения однослойного персептрона [1].
2 Метод Розенблатта
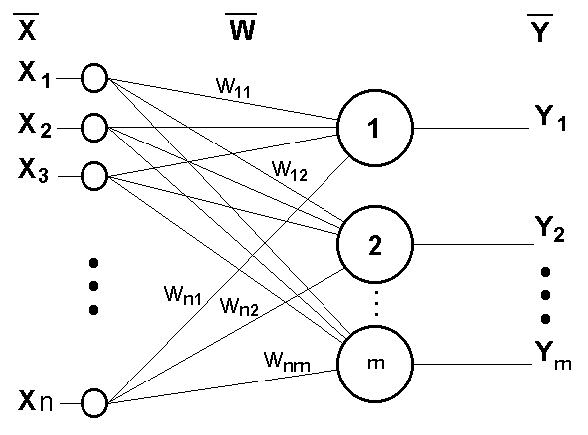
Данный метод был предложен Ф.Розенблаттом в 1959 г. для НС, названной персептрон (perceptron) [1]. Персептрон имеет пороговую функцию активации2; его схема представлена на рис.1.
Процедуру обучения Розенблатта для однослойного персептрона можно представить так [4] :
где
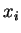 -
- 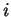 -тый
вход НС
-тый
вход НС 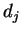 -
желаемый (идеальный)
-
желаемый (идеальный) 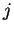 -тый выход НС
-тый выход НС 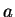 -
коэффициент (скорость обучения)
-
коэффициент (скорость обучения) 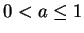
Весовые коэффициенты меняются только в том случае, если реальное выходное значение не совпадает идеальным выходным значением.
Полный алгоритм обучения Розенблатта строится следующим образом:
- весовые коэффициенты НС инициализируются малыми случайными значениями.
- подать на вход НС очередной учебный пример.
- если выход НС
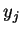 не совпадает
с идеальным выходом
не совпадает
с идеальным выходом 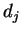
то происходит модификация весов по (1) - цикл с п.2
пока
не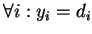
или
весовые коэф. перестанут меняться
3 Метод Видроу-Хоффа
Персептрон Розенблатта ограничивается бинарными выходами. Видроу и Хофф изменили модель Розенблатта. Их первая модель - ADALINE (Adaptive Linear Element) имела один выходной нейрон3 и непрерывную линейную функцию активации нейронов[3].
Метод обучения Видроу-Хоффа
известен еще как дельта-правило (delta-rule). Этот метод ставит своей
целью минимизацию функции ошибки ![]() в пространстве весовых коэффициентов.
в пространстве весовых коэффициентов.
где
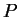 -
количество обработанных НС примеров
-
количество обработанных НС примеров 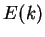 -
ошибка для
-
ошибка для 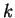 -го примера
-го примера 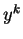 -
реальный выход НС для
-
реальный выход НС для 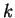 -го примера
-го примера 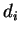 -
желаемый (идеальный) выход НС для
-
желаемый (идеальный) выход НС для 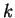 -го примера
-го примера
Минимизация ![]() осуществляется
методом градиентного спуска
осуществляется
методом градиентного спуска
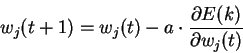
где
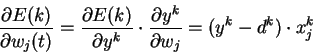
Таким образом весовые коэффициенты изменяются по правилу
Полный алгоритм обучения методом Видроу-Хоффа строится следующим образом:
- задать
скорость обучения
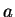 (
(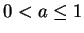 )
)
задать минимальную ошибку сети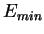 ;
;
весовые коэффициенты НС инициализируются малыми случайными значениями. - подать на
вход НС очередной учебный пример
рассчитать выход НС - скорректировать веса по (4)
- цикл с п.2 пока
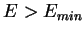
(где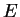 - суммарная среднеквадратичная ошибка НС)
- суммарная среднеквадратичная ошибка НС)
4 Метод обратного распространения
Сеть, имеющую два и более слоёв, уже проблематично обучить описанными выше методами, поскольку в многослойных сетях известен выход лишь последнего слоя нейронов.
Вариант решения этой задачи был предложен Д.Румельхартом с соавторами в 1986 году [2]. Предложенный метод обучения многослойного персептрона, был назван - методом обратного распространения ошибки. Основная идея метода состояла в распространение сигналов ошибки от выходов НС к ее входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы.
Метод обратного распространения ошибки (error back propagation - BP) это итеративный градиентный алгоритм обучения многослойных НС без обратных связей [2][6]. При обучении ставится задача минимизации функции ошибки:
где
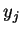 -
реальное значение
-
реальное значение 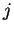 -того выхода НС;
-того выхода НС; 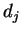 -
идеальное (желаемое) значение
-
идеальное (желаемое) значение 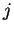 -того выхода НС;
-того выхода НС;
Минимизация ![]() ведется методом
градиентного спуска. Подстройка весовых коэффициентов происходит следующим
образом:
ведется методом
градиентного спуска. Подстройка весовых коэффициентов происходит следующим
образом:
где
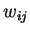 -
весовой коэффициент синаптической связи, соединяющей
-
весовой коэффициент синаптической связи, соединяющей 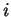 -ый и
-ый и 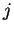 -ый
узлы НС;
-ый
узлы НС; 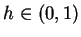 - коэффициент скорости обучения;
- коэффициент скорости обучения; - Второй множитель (6)
· Здесь
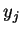 -
выход нейрона
-
выход нейрона 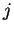 ,
, 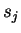 -
взвешенная сумма его входных сигналов, то есть аргумент активационной функции.
-
взвешенная сумма его входных сигналов, то есть аргумент активационной функции.
- Первый множитель в (7) раскладывается следующим образом:
где ![]() число нейронов слоя
число нейронов слоя ![]() .
.
Введя новую переменную
мы получим рекурсивную
формулу для расчетов величин ![]() слоя
слоя ![]() из величин
из величин ![]() слоя
слоя ![]() .
.
Для выходного слоя
Теперь мы можем записать (6) в раскрытом виде:
Полный алгоритм обучения НС с помощью процедуры обратного распространения ошибки строится следующим образом:
- Инициализировать случайным образом все весовые коэф.НС.
- Последовательно подать на вход HC все примеры из учебной выборки. Для каждого входа:
- Фаза
прямого распространения сигнала :
Вычислить выход каждого нейрона НС. - Фаза обратного распространения сигнала :
Для
выходного слоя вычислить изменения весов ![]()
по (12) и (11).
Для
всех остальных слоев вычислить ![]() по (12) и (10)
по (12) и (10)
![]()
- Скорректировать
все веса НС :
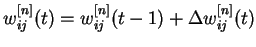
- Если
ошибка НС существенна, перейти на шаг 2,
иначе - конец работы.
Сноски
либо модификация архитектуры НС
функцию единичного скачка
более поздняя модель - MADALINE имела несколько выходных нейронов
таким, образом функция единичного скачка и прочие активационные функции с неоднородностями не подходят. В данном случае применяются гладкие функции - гиперболический тангенс или классический сигмоид с экспонентой
Литература
F.Rosenblatt ''Principles of
Neurodinamics.'' 1962, New York: Spartan Books.
Русский перевод:
Ф.Розенблатт ''Принципы нейродинамики.'' Москва ''Мир'' 1965.
D.E.Rumelhart, G.E.Hinton,
R.J.Williams
''Learning internal representations by error propagation.'' 1986.
In Parallel distributed processing, vol. 1, pp. 318-62. Cambridg, MA: MIT
Press.
В.Widrow, M.Hoff ''Adaptive switching circuits.'' 1960 IRE WESCON Convention Record, part 4, pp. 96-104. New York: Institute of Radio Engineers.
В.А.Головко, под ред.проф.А.И.Галушкина
''Нейронные сети: обучение, организация и применение'', ИПРЖР, Москва 2001
С.Короткий ''Нейронные сети'' - http://lii.newmail.ru/
Л.Г.Комарцова, А.В. Максимов ''Нейрокомпьютеры''
Москва, МГТУ им. Н.Э.Баумана, 2002
2003-07-18