Ознакомьтесь с Условиями пребывания на сайте Форнит Игнорирование означет безусловное согласие. СОГЛАСЕН

Книги сайта: «Мировоззрение», «Познай себя», «Основы адаптологии»,
«Вне привычного», Лекторий МВАП, «Что такое Я», «Наука», «Субъективность».

Этот материал взят из источника в свободном доступе интернета. Вся грамматика источника сохранена.

Основы квантовой механики А.В. Борисов

Относится к «Теории мироздания»

Физический факультет МГУ, 1998 г.

Уравнение Шредингера

Физические предпосылки создания квантовой механики

Атомные спектры излучения

Согласно экспериментальным данным, полученным к концу XIX века, частоты спектральных линий данного атома

$omega_{nn'}=T(n)-T(n')$

где T(n)- функция целого числа (спектральный терм), n=1,2,3,... . Это соотношение выражает комбинационный принцип Ритца (W. Ritz). В частности, для спектра излучения атома водорода Бальмер (J. Balmer) в 1885 г. эмпирически нашел простую формулу

$omega_{nn'}=Rleft( frac{1}{n'^2}-frac{1}{n^2}right),$

где R - постоянная Ридберга (J. Rydberg).
В классической теории для периодического движения заряженных частиц частоты излучения кратны основной частоте:

$omega_{n}=nomega_0, ; omega_0=frac{2pi }{tau},$

- период. Таким образом, эта теория не может объяснить комбинационный принцип.

Равновесие электромагнитного излучения и вещества

Рассмотрим замкнутый сосуд, нагретый до температуры T. Внутри него находится равновесное электромагнитное излучение: излучаемая и поглощаемая атомами вещества стенок сосуда в единицу времени энергии равны. Спектральная плотность энергии равновесного излучения - универсальная функция частоты и температуры

(не зависит от размеров и формы сосуда и вещества стенок). Из классической теории следует закон Рэлея (J. Rayleigh):

т.е. полная плотность (энергия в единице объема)

$intlimits_0^{infty}domegarho(omega, T)=infty,$

что означает невозможность равновесия в противоречии с экспериментом.
В 1900 г. Планк (M. Planck), анализируя механизм установления равновесия между веществом и излучением, выдвинул фундаментальную гипотезу квантования: вещество испускает энергию излучения конечными порциями (квантами), пропорциональными частоте излучения. Коэффициент пропорциональности - универсальная постоянная h, имеющая размерность механического действия. В простейшей модели вещества в виде атомных осцилляторов это означает, что энергия E осциллятора частоты

квантуется по закону

Здесь введена постоянная Планка

(сам Планк использовал вместо циклической частоты

линейную частоту

так что

).
Используя гипотезу квантования (противоречащую классической физике!), Планку удалось получить следующую формулу для спектральной плотности энергии равновесного излучения:

$rho(omega,T)=frac{hbaromega^3}{pi^2 c^3 (e^{hbaromega/k_{B}T}-1)},$

где скорость света c и постоянная Больцмана k_B(L. Boltzmann) известны из классической физики. Формула Планка прекрасно согласуется с экспериментом, позволяющим определить постоянную Планка (приводим современное значение): $hbar=1,05457266(63)cdot 10^{-27} ; эргcdot с.$

Фотоэффект

Планк приписал квантовые свойства атомным осцилляторам, а не излучению. В 1905 г. А. Эйнштейн (A. Einstein), развивая гипотезу Планка, сделал второй шаг: само электромагнитное излучение состоит из отдельных квантов - частиц, названных позже фотонами. Энергия фотона, отвечающего излучению частоты

, равна

Гипотеза Эйнштейна возникла при анализе фотоэффекта, открытого Герцем в 1887 г. (H. Hertz) и подробно исследованного А.Г. Столетовым в 1888-90 г. Эффект состоит в испускании веществом электронов под действием падающего на вещество излучения достаточно высокой частоты. Объяснение законов фотоэффекта следует из выведенного Эйнштейном уравнения:

$hbaromega=frac{mv^2}{2}+A,$

т.е. кинетическая энергия электрона - линейная функция частоты ( A - работа выхода, характерная для данного вещества) и не зависит от интенсивности излучения, что противоречит классической теории, но подтверждается экспериментом.

Эффект Комптона

В 1922 г. Комптон (A. Compton) обнаружил увеличение длины волны

рентгеновского излучения вследствие его рассеяния электронами вещества. Согласно же классической теории длины волн падающего и рассеянного излучения должны совпадать. Теория эффекта была построена Комптоном и независимо Дебаем (P. Debye) на основе фотонной гипотезы Эйнштейна. Взаимодействие излучения с электроном сводится к упругому столкновению фотона с покоящимся электроном. При этом импульс фотона определяется в виде

Здесь волновой вектор

${bf k}=frac{omega}{c}{bf n},$

n - единичный вектор в направлении распространения монохроматической волны, соответствующей фотону. Это определение - следствие того, что величины

$k^{mu}=left( frac{omega}{c},{bf k}right); и ; p^mu=left( frac{E}{c},{bf p}right)$

образуют 4-векторы относительно преобразований Лоренца (см. первую часть курса физики).
Запишем законы сохранения энергии и импульса для указанного процесса столкновения:

$hbar +mc^2=hbaromega' +E,; hbar{bf k}=hbar{bf k}'+{bf p},$

где $E=sqrt{m^2c^4+c^2{bf p}^2}$ - энергия электрона после столкновения. Отсюда получаем частоту рассеянного фотона:

$omega'=frac{omega}{1+frac{hbaromega}{mc^2}(1-costheta)},$

где

- угол между k и k' (угол рассеяния). Учитывая связь частоты и длины волны

находим изменение длины волны при рассеянии:

$Deltalambda=lambda'-lambda=4pi lambda_e sin^2frac{theta}{2}.$

Здесь введена комптоновская длина волны электрона

$lambda_e=frac{hbar}{mc}=3,86cdot 10^{-11} {rm см}.$

Для рентгеновского излучения (

~10^-9см) получаем

$frac{Deltalambda}{lambda}leq 4pi frac{lambda_e}{lambda}sim 0,! 1 ,$

т.е. вполне заметный эффект. Для видимого света (

~10^-5см) эффект гораздо меньше (~10^-5). Найденная зависимость изменения длины волны от угла рассеяния прекрасно согласуется с экспериментом.

Физические предпосылки создания квантовой механики

Атомные спектры излучения

Согласно экспериментальным данным, полученным к концу XIX века, частоты спектральных линий данного атома

$omega_{nn'}=T(n)-T(n')$

$omega_{nn'}=Rleft( frac{1}{n'^2}-frac{1}{n^2}right),$

$omega_{n}=nomega_0, ; omega_0=frac{2pi }{tau},$

- период. Таким образом, эта теория не может объяснить комбинационный принцип.

Равновесие электромагнитного излучения и вещества

(не зависит от размеров и формы сосуда и вещества стенок). Из классической теории следует закон Рэлея (J. Rayleigh):

т.е. полная плотность (энергия в единице объема)

$intlimits_0^{infty}domegarho(omega, T)=infty,$

квантуется по закону

Здесь введена постоянная Планка

(сам Планк использовал вместо циклической частоты

линейную частоту

так что

$rho(omega,T)=frac{hbaromega^3}{pi^2 c^3 (e^{hbaromega/k_{B}T}-1)},$

Фотоэффект

, равна

$hbaromega=frac{mv^2}{2}+A,$

Эффект Комптона

В 1922 г. Комптон (A. Compton) обнаружил увеличение длины волны

Здесь волновой вектор

${bf k}=frac{omega}{c}{bf n},$

$k^{mu}=left( frac{omega}{c},{bf k}right); и ; p^mu=left( frac{E}{c},{bf p}right)$

$hbar +mc^2=hbaromega' +E,; hbar{bf k}=hbar{bf k}'+{bf p},$

где $E=sqrt{m^2c^4+c^2{bf p}^2}$ - энергия электрона после столкновения. Отсюда получаем частоту рассеянного фотона:

$omega'=frac{omega}{1+frac{hbaromega}{mc^2}(1-costheta)},$

где

- угол между k и k' (угол рассеяния). Учитывая связь частоты и длины волны

находим изменение длины волны при рассеянии:

$Deltalambda=lambda'-lambda=4pi lambda_e sin^2frac{theta}{2}.$

Здесь введена комптоновская длина волны электрона

$lambda_e=frac{hbar}{mc}=3,86cdot 10^{-11} {rm см}.$

Для рентгеновского излучения (

~10^-9см) получаем

$frac{Deltalambda}{lambda}leq 4pi frac{lambda_e}{lambda}sim 0,! 1 ,$

т.е. вполне заметный эффект. Для видимого света (

Волновые свойства электронов

Итак, электромагнитное излучение обладает как волновыми, так и корпускулярными свойствами (корпускулярно-волновой дуализм). Этот дуализм неразрывно связан с существованием постоянной Планка

- кванта действия. Квантование действия можно получить, обобщив планковское правило квантования энергии осциллятора. Запишем гамильтониан осциллятора - интеграл движения:

$H(p,q)=frac{p^2}{2m}+frac{momega^2 q^2}{2}=E.$

Отсюда видно, что его фазовая траектория - эллипс с полуосями

и $b=sqrt{2E/momega^2}.$ Площадь эллипса

равна контурному интегралу по фазовой траектории (в классической механике он называется переменной действия):

где учтен планковский постулат. Мы получили правило квантования произвольной одномерной системы, совершающей периодическое движение. Оно впервые было выведено самим Планком.
В 1913 г. Бор (N. Bohr) применил это правило к атому водорода, рассмотрев частный случай движения электрона в кулоновском поле ядра по круговой орбите. Выбрав в качестве координаты азимутальный угол

, для соответствующего канонического импульса $p_{varphi}$ - интеграла движения получаем условие квантования:

$intlimits_0^{2pi}p_{varphi}dvarphi=2pi p_{varphi}=2pi nhbar, ; {rm или}; p_{varphi}=nhbar.$

Для частицы массы m, движущейся со скоростью v по окружности радиуса r (в плоскости (x,y)), имеем $p_{varphi}=mvr$ , т.е. $p_{varphi}$ - z-компонента момента импульса, или углового момента,

. Таким образом,

- квант углового момента.
Учтем уравнение движения электрона с зарядом - e в кулоновском поле ядра с зарядом e,

mv²/r=e²/r²,

и квантование момента:

Отсюда находим квантованные значения энергии электрона в атоме водорода:

$E_n=-frac{me^4}{2hbar^2}cdot frac{1}{n^2},; n=1,2,3,ldots$

Так Бор пришел к выводу о существовании дискретного множества стационарных состояний атома с энергиями E_n.
Далее он предположил, что излучение атома возникает при его переходе из одного стационарного состояние n в другое n' (с меньшей энергией). Частота соответствующей спектральной линии определяется правилом, следующим из закона сохранения энергии:

$omega_{nn'}=frac{1}{hbar}(E_n-E_{n'}).$

Это и есть знаменитое правило частот Бора. В соответствии с гипотезой Эйнштейна при переходе излучается фотон с энергией $hbar omega_{nn'}.$
Применив правило частот к атому водорода, Бор получил формулу Бальмера, найдя при этом выражение для постоянной Ридберга через фундаментальные физические постоянные:

$R=frac{me^4}{2hbar^3}.$

Вычисленное значение Rпрекрасно согласуется со значением, полученным из спектроскопических измерений.
Дальнейшее развитие теории Бора потребовало найти методы квантования систем с несколькими степенями свободы. Важный класс таких систем - квазипериодические системы с разделяющимися переменными. В этом случае правила квантования применяются к каждой независимой паре канонических переменных (p_i,q_i):

$oint p_i dq_i = 2pihbar n_i, ; i=overline{1,f}.$

Таким образом, число вводимых квантовых чисел n_i равно числу степеней свободы f. Условия квантования квазипериодических систем были сформулированы независимо Вильсоном и Зоммерфельдом (W. Wilson, A. Sommerfeld) в 1915-16 г. Применение этих условий к эллиптическим электронным орбитам в атоме водорода дало известный результат Бора для энергии стационарных состояний вследствие специфики кулоновского потенциала (совпадение периодов изменения разделяющихся сферических координат

, что приводит к зависимости квантованных значений энергии только от суммы целых чисел

).
Теория Бора-Зоммерфельда оказалась не в состоянии объяснить обнаруженную тонкую структуру атомных спектров и была непоследовательной: она использовала как классические представления, так и чуждые ей квантовые. В частности, электрон считался классической частицей, но из всего множества возможных траекторий отбирались лишь те, которые удовлетворяли условиям квантования.
В 1923 г. Л. де Бройль (L. de Broglie) выдвинул гипотезу, что электрон (и другие микрочастицы) не является классической корпускулой, но должен обладать также и волновыми свойствами. Тем самым де Бройль обобщил понятие эйнштейновского корпускулярно-волнового дуализма электромагнитного излучения. Согласно де Бройлю, частице с энергией E и импульсом p отвечает некоторая монохроматическая волна, частота и волновой вектор которой связаны с характеристиками частицы соотношениями

$omega=frac{E}{hbar}, ; {bf k}=frac{bf p}{hbar}$

Они в точности совпадают с соотношениями Эйнштейна для фотона и световой волны. Следовательно, дебройлевская длина волны частицы

$lambda=frac{2pi hbar}{p}.$

Правило квантования для одномерной частицы получает наглядную волновую интерпретацию:

$oint frac{dq}{lambda}=n,$

т.е. на длине траектории должно укладываться целое число длин волн (ср. с известным из школьного курса условием образования стоячих волн на струне с закрепленными концами).
Гипотеза де Бройля вскоре получила блестящее экспериментальное подтверждение: в 1927 г. Дэвиссон и Джермер (C. Davisson, L. Germer) наблюдали дифракцию пучка электронов на монокристалле никеля (периодической атомной структуре - аналоге используемой в оптике дифракционной решетке). Для использованных ими нерелятивистских электронов, получивших кинетическую энергию при прохождении разности потенциалов

, получаем

$frac{mv^2}{2}=ePhi,; lambda=frac{2pihbar}{mv}.$

Отсюда, выражая

в вольтах, получим длину электронной волны

$lambda=frac{1,! 2cdot 10^{-7}}{sqrt{Phi}} ; см.$

При

=100 В находим $lambdaapprox 10^{-8} ; см,$ что отвечает длине волны мягкого рентгеновского излучения и среднему межатомному расстоянию в кристаллической решетке. Поэтому при этих условиях дифракция электронов должна быть аналогична открытой еще в 1912 г. дифракции рентгеновских лучей, что и наблюдалось в действительности.

Волновое уравнение Шредингера

Получим уравнение для волны, сопоставляемой электрону. Примем простейшую гипотезу, что волновое поле описывается скалярной функций времени t и координат r=(x,y,z) точки наблюдения. По традиции эта функция обозначается

и называется волновой функцией.
Рассмотрим сначала частный случай монохроматической волны:

$psi=Ae^{-i(omega t-{bf kcdot r})}.$

В нашем курсе мы ограничимся нерелятивистскойтеорией, в которой энергия E свободной частицы массы m связана с ее импульсом p соотношением

E=p²/2m,

что дает следующую зависимость частоты дебройлевской волны

от волнового вектора k (закон дисперсии):

$omega=frac{hbar k^2}{2m}.$

Для монохроматической волны имеем

$frac{partial psi}{partial t}=-iomega t,; nabla=ikpsi, ; nabla^2psi= -k^2psi,$

и учет закона дисперсии приводит к дифференциальному уравнению для волновой функции

$.ihbar frac{partial psi}{partial t}=-frac{hbar^2}{2m}nabla^2psi.$

Это и есть уравнение Шредингера (E. Schrodinger) для свободной частицы, полученное им в 1926 г. Ввиду линейности этого уравнения (параболического типа) оно выполняется для произвольной суперпозиции монохроматических волн:

$psi(t,{bf r})=intfrac{d^3k}{(2pi)^{3/2}}C({bf k})e^{-i(omega t-{bf kr})},$

представляющей собой общее решение.
Возникает вопрос о связи уравнения Шредингера (УШ) и уравнений классической механики. Заметим, что фаза монохроматической волны связана с решением S(t,r) уравнения Гамильтона-Якоби (УГЯ) для свободной частицы

$frac{partial S}{partial t}+frac{1}{2m}(nabla S)^2=0$

очевидным соотношением

а сама волновая функция выражается через S в виде

$psi=e^{frac{iS}{hbar}}.$

Подставив это выражение в УШ, получим для S уравнение

$frac{partial S}{partial t}+frac{1}{2m}(nabla S)^2-frac{ihbar}{2m}nabla^2 S=0,$

которое отличается от УГЯ дополнительным слагаемым, пропорциональным постоянной Планка

, и эквивалентно УШ. В частном случае, когда S - линейная функция r, это слагаемое обращается в нуль. В общем же случае УШ для

переходит в УГЯ для S только в (формальном) пределе

Используем установленную связь УШ и УГЯ, чтобы найти УШ для частицы, движущейся в потенциальном силовом поле U(t,r). Запишем соответствующее классическое УГЯ:

$frac{partial S}{partial t}+frac{1}{2m}(nabla S)^2+U=0.$

Перейдем к новой функции $psi={rm exp}left( {frac{i}{hbar}S}right)$ . Для нее получаем:

$frac{partial psi}{partial t}=frac{i}{hbar}frac{partial S}{partial t}psi, ; nablapsi=frac{i}{hbar}(nabla S)psi, ; nabla^2psi=-frac{1}{hbar^2}[(nabla S)^2-ihbarnabla^2 S]psi.$

В силу УГЯ для S функция

удовлетворяет нелинейному уравнению. Однако для объяснения явлений интерференции и дифракции необходимо выполнение принципа суперпозиции. Поэтому уравнение для

должно быть линейным. Оно следует из квантового обобщения уравнения Гамильтона-Якоби (КУГЯ)

$frac{partial S}{partial t}+frac{1}{2m}(nabla S)^2+U-frac{ihbar}{2m}nabla^2 S=0$

и имеет вид:

$ihbarfrac{partial psi}{partial t}=hat Hpsi,; hat H=-frac{hbar^2}{2m}nabla^2+U(t,{bf r}).$

Это уравнение Шредингера для частицы в потенциальном поле. Введенный линейный оператор

называется оператором Гамильтона, или гамильтонианом.
Линейное УШ эквивалентно нелинейному КУГЯ, причем в общем случае как

, так и S- комплекснозначные функции. КУГЯ переходит в классическое УГЯ при условии

В этом приближении допустимо использовать классическое выражение для импульса

Тогда находим

$frac{hbar}{p^2}|nabla p|ll 1,$ или $frac{lambda |nabla p|}{p}ll 1,$

т.е. относительное изменение импульса на дебройлевской длине волны

должно быть малым.
В одномерном случае получаем простое условие

$|frac{dlambda}{dx}|ll 1,$

т.е.

должна слабо изменяться при изменении координаты x. При $frac{partial U}{partial t}=0$ выполняется закон сохранения энергии:

p²/2m + U(x)=E.

Отсюда находим

pdp/mdx=-dU/dx=F,

где F - ньютоновская сила. Условие применимости классического уравнения Гамильтона-Якоби принимает в стационарном одномерном случае вид:

$frac{lambda |F|}{p^2/m}ll 1,$

т.е. работа силы на дебройлевской длине волны должна быть мала по сравнению с кинетической энергией частицы. Это условие заведомо нарушается в окрестности точки поворота x=x₀, где p(x₀)=0, и, следовательно,

Более подробно условия применимости классической механики мы обсудим позже (см. п. 5).

Волновая функция

Волновой пакет и его эволюция

Рассмотрим специальное решение уравнения Шредингера для свободной частицы в одномерном случае:

$psi(t,x)=intlimits_{-infty}^{infty}dkC(k)e^{-i(omega t-kx)},$

где C(k) - функция, модуль которой имеет резкий максимум в некоторой точке k=k₀ и быстро убывает при

Такое решение называется волновым пакетом.
Ограничимся для определенности частным случаем прямоугольного пакета:

$C(k)=left{ begin{array}{l} A/delta={rm const}, kin I=(k_0-delta/2, k_0+delta/2), 0, knotin I, end{array}right.$

где

Вычислим интеграл по k приближенно, используя разложение частоты

в окрестности k₀:

$omega(k)=omega(k_0)+omega'(k_0)(k-k_0)+frac{1}{2}omega''(k_0)(k-k_0)^2+cdots.$

С учетом лишь линейных членов разложения получим пакет в виде

$psi(t,x)=B(t,x)e^{-i(omega_0 t-k_0 x)}.$

Здесь переменная амплитуда

$B(t,x)=frac{A}{delta}intlimits_{k_0-delta/2}^{k_0+delta/2} e^{i(k-k_0)(x-omega_0't)}dk = Afrac{sinxi}{xi}, ; xi=frac{delta}{2}(x-omega_0't),$

где $omega_0'=left(frac{domega}{dk}right)_{k=k_0}.$ При

пакет представляет собой амплитудно-модулированную волну - это почти монохроматическая волна, амплитуда которой заметно изменяется на сравнительно больших временном и пространственном интервалах:

В рассматриваемом случае амплитуда B(t,x) имеет максимум, равный A, в точке

Следовательно, максимум (центр пакета) движется равномерно со скоростью

$v_g=left(frac{domega}{dk}right)_{k=k_0},$

которая называется групповой скоростью (пакет

группа волн). Пакет

сосредоточен в окрестности максимума амплитуды B и имеет указанные выше размеры

в пространстве и во времени. Его фурье-образ

имеет соответственно размеры

причем выполнены соотношения

которые, конечно, известны в теории преобразования Фурье.
До сих пор мы не учитывали высшие члены разложения

. Учет слагаемого

в аргументе экспоненты в интегральном представлении пакета

приводит, очевидно, к расплыванию пакета, т.е. его уширению. Определим характерное время расплыванияпакета t_d из условия

отсюда с учетом связи

находим

$t_dsim frac{(Delta x)^2}{left( frac{d^2omega}{dk^2}right)_{k_0}}.$

Описанные выше свойства волнового пакета не зависят от природы волны. Волновая функция свободной частицы в виде пакета описывает суперпозицию состояний частицы с различными значениями импульса и энергии:

$p=hbar k,; E=hbar omega =frac{hbar^2 k^2}{2m}.$

Такая суперпозиция не имеет прямого аналога в классической механике. Тем не менее, косвенная связь с классикой есть: центр пакета движется равномерно с групповой скоростью

$v_g=left( frac{domega}{dk}right)_{k_0}=frac{hbar k_0}{m},$

что отвечает соотношению v=p/m для классической частицы, движущейся со скоростью v=v_g.
Попытка представить квантовую частицу в виде некоторого материального волнового сгустка (пакета) не выдерживает критики, в частности, ввиду расплывания пакета. Действительно, время расплывания пакета начальной ширины a для нерелятивистской частицы (E=p²/2m) равно

$t_dsim frac{a^2}{hbar (d^2E/dp^2)}=frac{ma^2}{hbar}.$

Положим a=10^-8см (типичный размер атома, см. п.10) и m=9,1*10^-28г (масса электрона). Тогда время расплывания

t_d~10^-27г*10^-16см²/10^-27эрг*с=10^-16с.

Следовательно, с макроскопической точки зрения пакет расплывается мгновенно. За время t_d ширина пакета возрастает по определению на величину порядка a. Следовательно, скорость расплывания

$v_dsim frac{a}{t_d}simfrac{hbar}{ma}.$

В нашем примере за время t=1c ширина первоначально микроскопического пакета достигнет величины

$frac{hbar t}{ma}sim frac{10^{-27}cdot 1}{10^{-27}cdot 10^{-8}}=10^8 см=10^3 км!$

С другой стороны, для макроскопической частицы массы m=1г положим a=1см. Тогда время расплывания

t_d~1*1/10^-27=10²⁷c,

что гораздо больше времени жизни Вселенной

Иначе говоря, за 1 с пакет расширится на ничтожную величину

10^-27*1/1*1=10^-27см.

Следовательно, для макроскопической частицы расплыванием пакета можно пренебречь. С высокой степенью точности движение центра макроскопически малого пакета подчиняется законам классической механики (см. п. 5).
Для микрочастицы в общем случае необходимо использовать уравнение Шредингера для волновой функции, которой, как мы убедились, нельзя придать непосредственно прямой физический смысл.

Вероятностная интерпретация волновой функции

Представление об электроне в виде группы волн находится в явном противоречии с экспериментами по столкновению электронов с атомами, в которых электрон ведет себя как единая стабильная частица. В экспериментах по дифракции пучка электронов на кристаллах проявляются волновые свойства электронов, причем аналогия с дифракцией электромагнитных волн, рассматриваемых как поток фотонов, приводит к статистическому предположению: интенсивность волны в данной точке пространства пропорциональна плотности частиц. Оказывается, однако, что дифракционная картина не зависит от интенсивности пучка частиц: она возникает и при очень малой интенсивности и даже при пропускании одиночных электронов один за другим. При регистрации дифракционной картины каждый электрон, прошедший периодическую структуру (например, монокристалл), оставляет на фотопластинке небольшое пятно, проявляя тем самым корпускулярные свойства. При достаточно большем числе прошедших последовательно электронов распределение пятен на пластинке образует дифракционную картину, совпадающую с получаемой при пропускании пучка электронов.
Детальный анализ процессов рассеяния электронов на атомах на основе уравнения Шредингера привел Борна (M. Born) к вероятностной интерпретации волновой функции частицы (1926 г.): квадрат модуля $|psi(t,{bf r})|^2$ есть плотность вероятности обнаружить частицу в точке пространства r в момент времени t. Таким образом, квантовая механика (даже для одной частицы) является вероятностной теорией, в которой принцип причинности отличается от соответствующего лапласовского принципа причинности в классической механике. В своей статье 1926 г. Борн так сформулировал основную особенность квантовой теории: "Движение частицы следует вероятностным законам, сама же вероятность распространяется в соответствии с законом причинности".
Указанная вероятностная интерпретация волновой функции - один из основных постулатов квантовой теории, который подтвержден всей совокупностью проведенных экспериментов.
Покажем, что из УШ вытекает закон сохранения вероятности. Запишем уравнения для

и комплексно сопряженной к ней функции

$ihbar frac{partial psi}{partial t}=-frac{hbar^2}{2m}nabla^2psi+Upsi, ; -ihbar frac{partial psi^*}{partial t}=-frac{hbar^2}{2m}nabla^2psi^*+Upsi^*.$

Умножив первое уравнение на

, а второе на

, вычтем одно из другого. Получим

$frac{partial}{partial t}(psi^*psi)=-frac{hbar}{2mi}(psi^*nabla^2psi-(nabla^2psi^*)psi)=-frac{hbar}{2mi}nabla(psi^*nablapsi-(nablapsi^*)psi).$

Введем плотность

и поток вероятности j:

$rho=psi^*psi=|psi|^2,; {bf j}=frac{hbar}{2mi}(psi^*nablapsi-(nablapsi^*)psi).$

В результате находим уравнение непрерывности (ср. с электродинамикой, ч. 1 курса):

$frac{partialrho}{partial t}+nablacdot{bf j}=0.$

Проинтегрировав его по объему V, ограниченному замкнутой поверхностью S, получим интегральный закон сохранения вероятности:

$frac{d}{dt}intlimits_V rho d^3x=-ointlimits_S ({bf jcdot n})dS.$

Удалив S в бесконечность, в предположении, что

${bf j}!left|_{|{bf r}|to infty}to 0right. ,$

получим

$frac{d}{dt}intlimits_V rho d^3 x=0,$

или

$int |psi|^2 d^3 x={rm const}.$

Для физически реализуемых состояний всегда можно выбрать такую нормировку волновой функции, что

Это соотношение означает, что вероятность обнаружить частицу во всем пространстве равна единице, как и должно быть.
Замечание. Плотность

и поток вероятности j инвариантны относительно преобразования фазы волновой функции:

$psito psi'=e^{ialpha}psi,; psi^*topsi'^*=e^{-ialpha}psi^*.$

Функции

и отвечают одному и тому же состоянию.

Наблюдаемые и операторы. принцип суперпозиции

Средние значения координаты и импульса. Наблюдаемые

Зная плотность вероятности координаты частицы, можно найти среднее значение координаты - математическое ожидание:

$lt {bf r} gt =int {bf r}|psi|^2 d^3 x.$

Как найти среднее значение импульса <p>? Рассмотрим волновой пакет:

$psi({bf r})= int frac{d^3 k}{(2pi)^{3/2}}C({bf k})e^{i{bf kr}},; C({bf k})= int frac{d^3 k}{(2pi)^{3/2}}psi({bf r})e^{-i{bf kr}}.$

Здесь время t фиксировано и явно не указано в качестве одного из аргументов волновой функции (ВФ). Преобразуем условие нормировки ВФ:

$intpsi^*({bf r})psi({bf r})d^3 x=1=int frac{d^3 kd^3 k'}{(2pi)^{3}}C^*({bf k})C({bf k'})int d^3 x e^{-i{bf kr}+i{bf k'r}}=int d^3 k C^*({bf k})C({bf k'}).$

Здесь использовано известное соотношение:

$int d^3 x e^{i{bf (k'-k)r}}=(2pi)^3delta({bf k'-k}).$

Естественно, следуя Борну, интерпретировать |C(k)|² как плотность вероятности обнаружить при измерении импульс частицы

. Фурье-образ C(k) функции

называется волновой функцией в импульсном представлении. Ясно, что тогда среднее значение импульса

$lt {bf p} gt =int d^3 k hbar {bf k} |C({bf k})|^2=int d^3 kint frac{d^3 x'}{(2pi)^{3/2}}psi^*({bf r'})e^{i{bf kr'}}int frac{d^3 x}{(2pi)^{3/2}}psi({bf r})ihbar (nabla e^{-i{bf kr}}).$

Проинтегрировав в последнем интеграле по частям в предположении, что $psi! left|_{|{bf r}|to infty}to 0right.$ , получим с учетом

$int d^3 k e^{i{bf k(r'-r)}}=(2pi)^3delta({bf r'-r})$

выражение для среднего импульса в координатном представлении:

$lt {bf p} gt =int d^3 x psi^*({bf r})(-ihbarnablapsi({bf r})).$

Итак, в пространстве волновых функций импульсу соответствует дифференциальный оператор:

. Координате отвечает оператор умножения:

${bf rto hat r=r},; lt {bf r} gt =int d^3 xpsi^*({bf r}){bf r}psi({bf r}).$

Заметим, что в пространстве волновых функций в импульсном представлении C(p) имеем:

${bf hat p=p}=hbar{bf k}, ; {bfhat r}=ihbarnabla_{{bf p}}=ihbarfrac{partial}{partial {bf p}}.$

Поэтому, в частности, средняя координата

$lt {bf r} gt =int d^3 pC^*({bf p})ihbarnabla_{{bf p}}C({bf p}).$

Полученные результаты обобщаются следующим образом: каждой физической величине A, значение которой может быть в принципе измерено, -наблюдаемой однозначно соответствует линейный оператор

в пространстве волновых функций.
Фундаментальный оператор Гамильтона - гамильтониан, определяющий эволюцию волновой функции, выражается через операторы координаты и импульса:

$hat H=frac{{bfhat P}^2}{2m}+U({bfhat r}).$

Среднее значение наблюдаемой вычисляется по правилу:

В дальнейшем будем использовать обозначения из функционального анализа, предполагая, что множество волновых функций - линейное пространство. Скалярное произведение:

$(psi,varphi)=intpsi^* varphi d^3 x,; (cpsi,varphi)=c^* (varphi,psi)^* ,; c={rm const}.$

Норма

вектора

определена в виде

причем

тогда и только тогда, когда

.
Оператору

ставится в соответствие эрмитово сопряженный оператор

согласно определению:

. Пусть

- оператор наблюдаемой A. Ее среднее значение должно быть действительным числом. Поэтому

Следовательно, оператор наблюдаемой должен быть эрмитовым:

. Легко проверить, что уже введенные операторы координаты и импульса эрмитовы в пространстве квадратично интегрируемых функций.

Принцип суперпозиции

Линейность уравнения Шредингера и операторов наблюдаемых обеспечивает выполнение фундаментального принципа суперпозиции, согласно которому:

Если квантовая система может находиться в состояниях, описываемых волновыми функциями

то она может также находиться и в состоянии

где c₁,c₂- произвольные комплексные числа.

Функции

, где с - произвольное комплексное число, описывают одно и то же состояние.
Для физически реализуемых состояний

. Принцип суперпозиции (см. п. 2) всегда позволяет выбрать для таких состояний условие нормировки

. Рассмотрим состояние

, представляющее собой суперпозицию состояний

. Для плотности вероятности, квадрата нормы и среднего значения наблюдаемой A в этом состоянии получаем соответственно выражения:

$begin{array}{l}|psi|^2=|c_1|^2|psi_1|^2+|c_2|^2|psi_2|^2+2{rm Re}c_1^* c_2psi_1^* psi_2, (psi,psi)=1=|c_1|^2+|c_2|^2+2{rm Re}c_1^* c_2(psi_1,psi_2), lt A gt =(psi,hat Apsi)=|c_1|^2(psi_1,hat Apsi_1)+|c_2|^2(psi_2,hat Apsi_2)+2{rm Re}c_1^* c_2(psi_1,hat Apsi_2).end{array}$

Отсюда видно, что квантовая механика не сводится к классической теории вероятности: возникает характерный эффект интерференции состояний

не имеющий классического аналога.

Условия одновременной измеримости наблюдаемых

Как мы уже видели, предсказания квантовой теории носят вероятностный характер. Выясним, когда измерение наблюдаемой A дает определенный результат. Рассмотрим отклонение от среднего

. Ему отвечает наблюдаемая

, где

- единичный оператор (в дальнейшем его будем опускать). Дисперсия случайной переменной A в состоянии

равна

Она обращается в нуль только при

, или

Следовательно, в указанном состоянии наблюдаемая имеет определенное значение, которое совпадает с одним из собственных значений оператора наблюдаемой. Само состояние описывается волновой функцией, представляющей собой собственный вектор оператора.
В дальнейшем для краткости, если это не приведет к недоразумению, мы будем отождествлять понятия состояния и соответствующей ему волновой функции (используется также термин вектор состояния), наблюдаемой и оператора наблюдаемой.
Пусть наблюдаемая

имеет дискретный спектр:

причем система собственных функций ${psi_n}$ полна и ортонормированна, т.е. образует базис в пространстве состояний:

$psi=sumlimits_{n}^{}c_npsi_n,; (psi_{n'},psi_n)=delta_{n'n},; c_n=(psi_n,psi).$

Здесь

- произвольный вектор с единичной нормой. Имеем следующие соотношения:

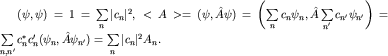$(psi,psi)=1=sumlimits_{n}^{}|c_n|^2,; lt A gt =(psi,hat Apsi)=left(sumlimits_{n}^{}c_n psi_n , hat A sumlimits_{n'}^{}c_{n'}psi_{n'}right)=sumlimits_{n,n'}^{}c^*_n c_n' (psi_n,hat Apsi_{n'})=sumlimits_{n}^{}|c_n|^2 A_n.$

Отсюда следует, что

есть вероятность получить значение A_n наблюдаемой A при измерении в состоянии

, причем значений

на опыте обнаружить нельзя.
Если наблюдаемая

имеет непрерывный спектр

, то

$psi=int c_{lambda}psi_{lambda}dlambda, ; c_{lambda}=(psi_{lambda},psi).$

Тогда

$w(lambda)=|c_{lambda}|^2$

- плотность вероятности, т.е.

- вероятность обнаружить значение A в интервале

При этом

Условие ортонормированности заменяется условием нормировки на

-функцию:

$(psi_{lambda'},psi_{lambda})=delta(lambda'-lambda).$

Пример. Собственные векторы оператора импульса

имеют вид

$psi_{bf p}({bf r})=(2pihbar)^{-3/2}{rm exp}left(frac{i}{hbar}{bf pcdot r}right),; (psi_{bf p'},psi_{bf p})=delta({bf p'-p}).$

Для оператора координаты

имеем

$psi_{bf r_0}({bf r})=delta({bf r-r_0}).$

В общем случае смешанного спектра получаем

$psi=sumlimits_{n}^{}c_npsi_n+int dlambda c_{lambda}psi_{lambda}, ; (psi,psi)=sumlimits_{n}^{}|c_n|^2+int dlambda |c_n|^2=1.$

Условие полноты системы собственных функций имеет вид:

$sumlimits_{n}^{}psi_n({bf r})psi_n^*({bf r'})+int dlambdapsi_n({bf r})psi_n^*({bf r'})=delta({bf r-r'}).$

Рассмотрим условия, при которых две наблюдаемых A и B могут быть одновременно измерены. Пусть в некотором состоянии они имеют определенные значения. Тогда, как мы уже знаем, вектор состояния должен быть собственным для операторов

$hat Apsi_{nm}=A_npsi_{nm},; hat Bpsi_{nm}=B_npsi_{nm}.$

Предположим, что ${psi_{nm}}$ образуют полную систему собственных векторов. Тогда для произвольного вектора состояния

$psi=sumlimits_{nm}^{}c_{nm}psi_{nm}$

имеем

$(hat Ahat B-hat Bhat A)psi=sumlimits_{nm}^{}(A_n B_m- B_m A_n)psi_{nm}=0.$

Ввиду произвольности

получаем операторное равенство

т.е. наблюдаемые должны коммутировать.
Это утверждение обобщается на случай произвольного (смешанного) спектра и представляет собой известную теорему из функционального анализа: если два оператора имеют общий полную систему собственных векторов, то они коммутируют. Справедлива и обратная теорема: если

то операторы

и имеют общую систему собственных функций.
Определим полный набор коммутирующих наблюдаемых

операторы

попарно коммутируют, $[hat A_i,hat A_j]=0;; i,j=overline{1,n};$

ни один из операторов

не является функцией от остальных;

любой оператор, коммутирующий со всеми

, есть функция от этих операторов.
Из изложенного выше следует,что существует общая полная система собственных векторов полного набора наблюдаемых:

$hat A_i psi_{lambda_1,ldots,lambda_n}=lambda_i psi_{lambda_1,ldots,lambda_n}, ; i=overline{1,n}.$

Поэтому произвольный вектор состояния может быть представлен в виде

$psi=sumlimits_{{lambda_1,ldots,lambda_n}}^{}c_{lambda_1,ldots,lambda_n}psi_{lambda_1,ldots,lambda_n},$

причем $|c_{lambda_1,ldots,lambda_n}|^2$ есть вероятность получить в результате одновременного измерения наблюдаемых

значения ${lambda_1,ldots,lambda_n}$ .
Таким образом, состояние системы в квантовой механике можно задать полным набором значений наблюдаемых. Их число называется числом степеней свободы системы. В общем случае оно определяется из опыта. В частных случаях это число совпадает с числом степеней свободы соответствующей классической системы.
Полный набор наблюдаемых может быть задан многими способами. Его фиксация определяет некоторое представление пространства состояний квантовой системы функциями

$psi({lambda_1,ldots,lambda_n})equiv c_{lambda_1,ldots,lambda_n}=(psi_{lambda_1,ldots,lambda_n}, psi),$

определенными на спектре операторов

. Функция $psi({lambda_1,ldots,lambda_n})$ называется волновой функцией системы в данном представлении.
Пример. Для точечной (бесструктурной) частицы полный набор наблюдаемых образуют операторы координат

Ему отвечает координатное представление волновых функций:

Другой полный набор составляют операторы компонент импульса $hat p_{x},hat p_{y},hat p_{z}:$

$psi(x,y,z)=intpsi(p_x,p_y,p_z){rm exp}left[frac{i}{hbar}(p_x x +p_y y+p_z z)right]frac{dp_x dp_y dp_z}{(2pihbar)^{3/2}},$

, где

- волновая функция в импульсном представлении (выше она обозначалась C(p)).

Соотношение неопределенностей гейзенберга. основные постулаты квантовой механики

Соотношение неопределенностей

Пусть две наблюдаемых

не коммутируют. Тогда их коммутатор имеет вид:

где

- эрмитов оператор. Покажем, что дисперсии наблюдаемых в произвольном состоянии

удовлетворяют ограничению

$left lt (Delta A^2)right gt left lt (Delta B)^2 right gt ge frac{1}{4} left lt C^2 right gt .$

Оно называется соотношением неопределенностей и получено впервые Гейзенбергом (W. Heisenberg) в 1927 г. для частного случая наблюдаемых

Его общее доказательство принадлежит Вейлю (H. Weyl). Введем наблюдаемые

и рассмотрим неотрицательную функцию действительного параметра

$begin{array}{c}F(lambda)=|lambdahat a-ihat b|^2=((lambdahat a-ihat b)psi,lambdahat a-ihat bpsi)=(psi,(lambdahat a+ihat b)(lambdahat a-ihat b)psi)= =(psi,(lambda^2hat a^2+hat b^2+lambda hat C)psi)=lambda^2 lt a^2 gt +lambda lt C gt + lt b^2 gt ge 0.end{array}$

Ввиду произвольности

дискриминант полученного квадратного трехчлена должен быть неположительным:

С учетом равенства

получаем отсюда приведенное выше соотношение неопределенностей (СН).
Для коммутирующих наблюдаемых правая часть СН обращается в нуль, что соответствует, как мы видели выше (см. п. 3), одновременной измеримости таких наблюдаемых.
Для некоммутирующих наблюдаемых СН накладывает ограничение на точности, с которыми могут быть одновременно заданы (измерены) эти наблюдаемые. Наиболее сильное ограничение имеется в случае, когда

для любых состояний

, например, если

где c=const. В этом случае не существует состояний, в которых обе наблюдаемых имеют определенные значения.
Пример. Пусть

Тогда

и мы получаем соотношение неопределенностей Гейзенберга:

$lt (Delta x)^2 gt lt (Delta p_x)^2 gt ge frac{hbar^2}{4}.$

Качественно СН может быть получено из анализа эволюции волнового пакета (см. п. 2). Было показано, что эффективные размеры пакета в координатном и импульсном представлениях, т.е. неопределенности координаты и импульса частицы, связаны соотношением

или

так как импульс

Детальный анализ показывает, что в случае некоммутирующих наблюдаемых

и измерение одной из них приводит к неконтролируемому изменению другой наблюдаемой. Возмущение системы в процессе измерения конечно и таково, что всегда выполняются СН. Иными словами, для точного измерения таких наблюдаемых требуются несовместимые измерительные приборы.
Найдем состояния

, в которых достигается минимум неопределенностей,т.е. точное равенство в СН. Получаем для них систему уравнений (см. выше вывод СН):

$(lambdahat a-ihat b)psi=0,; lambda^2 lt a^2 gt + lambda lt C gt + lt b^2 gt =0,; lt A^2 gt lt b^2 gt =frac{1}{4} lt C gt ^2.$

Отсюда находим

$lambda=-frac{ lt C gt }{2 lt a^2 gt },$

и уравнение для определения состояния, минимизирующего произведение неопределенностей, принимает вид:

$left(frac{ lt C gt }{2 lt a^2 gt }hat a+ihat bright)psi=0.$

Рассмотрим случай координаты и импульса:

В координатном представлении

и получаем уравнение:

$left[frac{d}{dx}+frac{x-x_0}{2sigma^2}-frac{p_0}{hbar}right]psi(x)=0.$

Здесь

Нормированное решение имеет вид:

$psi(x)=(2pisigma^2)^{-1/4}{rm exp}left[-frac{(x-x_0)^2}{4sigma^2}+frac{i}{hbar}p_0 xright].$

В этом состоянии

$lt (Delta x)^2 gt lt (Delta p_x)^2 gt =frac{hbar^2}{4}.$

СН "координата-импульс" выражает отсутствие точной траектории у частицы. В частности, нельзя определить импульс в данной точке пространства (как в классической механике): импульс характеризует состояние квантовой частицы в целом. Он может быть измерен, например, путем анализа дифракционной картины, образуемой при прохождении пучка частиц через периодическую структуру, с помощью дебройлевского соотношения между длиной волны и импульсом:

Основные постулаты квантовой механики

Мы ввели основные понятия квантовой механики и можем теперь явно сформулировать, следуя Дж. фон Нейману (J. von Neumann), ее основные постулаты:

Состояния системы описываются ненулевыми векторами

комплексного сепарабельного гильбертова пространства H, причем векторы

описывают одно и то же состояние тогда и только тогда, когда

, где c - произвольное комплексное число. Каждой наблюдаемой однозначно сопоставляется линейный эрмитов оператор

Наблюдаемые одновременно измеримы тогда и только тогда, когда соответствующие им эрмитовы операторы коммутируют.
В результате измерения наблюдаемой, представляемой оператором

может быть получено лишь одно из собственных значений

оператора

Вероятность w_n получить значение

при измерении в состоянии

равна

w_n=|c_n|²,

где c_n - коэффициент в разложении

по полной системе собственных функций

оператора

$psi=sumlimits_{n}^{}c_npsi_n,; c_n=(psi_n,psi).$

Эволюция системы определяется уравнением Шредингера

$ihbarfrac{partialpsi}{partial t}=hat Hpsi,$

где

- гамильтониан.

Каждому вектору

из пространства H отвечает некоторое состояние системы, любой эрмитов оператор

соответствует некоторой наблюдаемой.
Рассмотренный в п. 3 принцип суперпозиции, как легко проверить, следует из постулата П4.
Замечание 1. Выбор пространства H и закона соответствия

для конкретной физической системы определяется согласием предсказаний теории с результатами эксперимента. Этот выбор не может быть формализован: можно построить бесконечно много квантовых теорий, которые в пределе

переходят в одну и ту же классическую теорию.
Замечание 2. Существуют правила суперотбора, согласно которым пространство состояний H разбивается в прямую сумму ортогональных подпространств, причем сумма векторов из разных подпространств не может соответствовать физически реализуемому состоянию. Например, запрещена суперпозиция состояний с различными электрическими зарядами.

Изменение наблюдаемых со временем

Эволюция средних значений наблюдаемых

Пусть

- произвольное состояние, эволюционирующее во времени согласно уравнению Шредингера

$ihbarfrac{partialpsi}{partial t}=hat Hpsi.$

Получим уравнение для изменения среднего значения наблюдаемой

в этом состоянии. Имеем

$frac{d lt A gt }{dt}=left(frac{partialpsi}{partial t},hat Apsiright)+ left(psi,frac{partialhat A}{partial t}psiright)+ left(psi,hat A frac{partialpsi}{partial t}right)=-frac{1}{ihbar}(hat Hpsi,hat Apsi)+ frac{1}{ihbar}(psi,hat Ahat Hpsi)+ left( psi, frac{partialhat A}{partial t}psi right)=left(psi, left( frac{partial hat A}{partial t}+ frac{i}{hbar} [hat H, hat A] right)psiright).$

Здесь учтена эрмитовость

Итак,

$frac{d lt A gt }{dt}=left lt frac{partial hat A}{partial t}+ frac{i}{hbar} [hat H, hat A] right gt .$

Это уравнение - квантовый аналог классического уравнения для динамической переменной A(q,p,t):

$frac{dA}{dt}=frac{partial A}{partial t}+{H,A},$

где введена скобка Пуассона

${H,A}=sumlimits_{k}^{}left( frac{partial H}{partial p_k} frac{partial A}{partial q_k} -frac{partial H}{partial q_k} frac{partial A}{partial p_k}right).$

Таким образом, при переходе к квантовой теории

${H,A}to frac{i}{hbar} [hat H, hat A].$

Заметим, что алгебраические свойства скобки Пуассона совпадают со свойствами коммутатора наблюдаемых.
Определим оператор производной по времени:

$hat{dot A}equiv frac{partialhat A}{partial t}+frac{i}{hbar} [hat H, hat A].$

Тогда

$frac{d lt A gt }{dt}=(psi,hat{dot A}psi)= lt hat{dot A} gt .$

Пусть наблюдаемая

явно не зависит от времени и коммутирует с гамильтонианом:

$frac{partialhat A}{partial t}=0$ и $[hat H,hat A]=0$

Тогда в любом состоянии

среднее значение наблюдаемой <A>=const. В этом случае

называется интегралом квантовых уравнений движения.

Стационарные состояния

Рассмотрим важный частный случай независящего от времени гамильтониана:

$frac{partialhat H}{partial t}=0$

В этом случае существуют специальные решения уравнения Шредингера, которые легко получаются методом разделения переменных:

$psi_E={rm exp}left(-frac{i}{hbar}Etright)varphi_E,$

где

не зависят от времени и являются (как и

) собственными векторами гамильтониана:

Собственные значения E являются допустимыми значениями энергии системы, так как гамильтониан - оператор энергии, соответствующий классической функции Гамильтона.
Состояния

называются стационарными состояниями. Их основные свойства таковы:

плотность вероятности и поток вероятности в этих состояниях не зависят от времени:

$frac{partialrho}{partial t}=0,; frac{partial{bf j}}{partial t}=0.$

Средние значения наблюдаемых не зависят от времени:

$lt A gt =(psi_E,hat Apsi_E)=(varphi_E,hat Avarphi_E)={rm const}$ при $frac{partialhat A}{partial t}.$

Вероятность обнаружить собственное значение

наблюдаемой

не зависит от времени:

$w(lambda)=|(psi_lambda,psi_E)|^2={rm const}.$

Произвольное (нестационарное) состояние может быть разложено по стационарным состояниям - собственным векторам гамильтониана:

$psi(t,{bf r})=sumlimits_{n}^{}c_nvarphi_n({bf r}){rm exp}left(-frac{i}{hbar} E_n t right).$

В нестационарном состоянии энергия не имеет определенного значения, но среднее значение ее от времени не зависит:

$lt E gt =(psi,hat Hpsi)=sumlimits_{n}^{}|c_n|^2 E_n={rm const},$

так как

- интеграл движения:

$hat{dot H}=frac{i}{hbar}[hat H,hat H]=0.$

Если наблюдаемая

не коммутирует с гамильтонианом, то ее среднее, как и должно быть, зависит от времени (даже при $frac{partialhat A}{partial t}=0$ ):

$lt A gt =sumlimits_{n,n'}^{}c_n^*c_n'(varphi_n,hat Avarphi_n'){rm exp}[frac{i}{hbar}(E_n-E_{n'})t].$

Присутствие здесь недиагональных матричных элементов оператора наблюдаемой

отражает характерный квантовомеханический эффект интерференции различных стационарных состояний.
Легко проверить, что в нестационарном состоянии

и j также зависят от времени.

Теоремы Эренфеста

Рассмотрим подробнее случай одномерного движения частицы в поле U(x). Гамильтониан

$hat H=frac{hat p_x^2}{2m}+U(hat x).$

Учитывая фундаментальный коммутатор

, вычислим по общему правилу (см. выше) оператор скорости:

$hat{dot x}=frac{i}{hbar}[hat H,hat x]=frac{i}{2mhbar}[hat p_x^2,hat x]; ; [hat p_x^2,hat x]= hat p_x^2hat x-hat xhat p_x^2+ hat p_xhat xhat p_x-hat p_xhat xhat p_x= hat p_x[hat p_x,hat x]+[hat p_x,hat x]hat p_x=-2ihbarhat p_x.$

В результате

$hat{dot x}=frac{hat p_x}{m}.$

$hat{dot p_x}=frac{i}{hbar}[hat H,hat p_x]=frac{i}{hbar}[U(hat x),hat p_x]$

Последний коммутатор проще всего вычислить в координатном представлении:

$[U(hat x),hat p_x]=-ihbarleft[ U(x),frac{partial}{partial x}right]= ihbarfrac{partial U}{partial x}.$

В результате получим:

$hat{dot p_x}=-frac{partial U(hat x)}{partial hat x}.$

Отсюда для средних значений следуют уравнения, впервые полученные Эренфестом (P. Ehrenfest) в 1927 г.:

$frac{d lt x gt }{dt}=frac{ lt p_x gt }{m},; frac{d lt p_x gt }{dt}=-left lt frac{partial U}{partial x}right gt .$

Это, очевидно, квантовый аналог системы канонических уравнений Гамильтона. Отсюда следует квантовое обобщение закона Ньютона:

$mfrac{d^2 lt x gt }{dt^2}=-left lt frac{partial U}{partial x}right gt .$

Эти уравнения выражают содержание теорем Эренфеста.
Рассмотрим переход к классическим уравнениям движения. Пусть состояние

представляет собой волновой пакет, сосредоточенный в окрестности точки x=<x>. Разложив силу

в ряд по

и усреднив по пакету, получим с точностью до членов второго порядка малости уравнение движения

$mfrac{d^2 lt x gt }{dt^2}=F( lt x gt )+frac{1}{2}F''( lt x gt ) lt (Delta x)^2 gt +cdots.$

Здесь учтено, что

При условии

$lt (Delta x)^2 gt ll 2 left| frac{F( lt x gt )}{F''( lt x gt )}right|$

движение центра волнового пакета описывается классическим уравнением Ньютона. Этого условия, однако, недостаточно. Надо учесть соотношение неопределенностей

$lt (Delta x)^2 gt lt (Delta p_x)^2 gt ge frac{hbar^2}{4}$

и потребовать относительной малости флуктуаций импульса около среднего значения <p_x>:

при

$lt p_x gt ^2gg left lt (Delta p_x)^2right gt ge frac{hbar^2}{4 lt (Delta x)^2 gt }$

В этом приближении получаем классическую функцию Гамильтона:

$lt H(hat x, hat p_x) gt cong H( lt x gt , lt p_x gt )=frac{ lt p_x gt ^2}{2m}+U( lt x gt ),$

и можно говорить о движении центра пакета по траектории.
Указанные два условия одновременно выполняются при движении частицы с относительно большим импульсом в плавно меняющемся внешнем поле.

Интегралы движения и симметрия в квантовой механике

Вернемся к интегралам движения в квантовой механике и покажем, что их существование связано с симметрией системы. Ограничимся случаем

. Пусть спектр гамильтониана инвариантен относительно некоторых преобразований векторов состояний:

где

- линейный оператор. Инвариантность означает, что из уравнения

следует такое же уравнение для преобразованного вектора:

Отсюда получаем условие инвариантности гамильтониана:

$hat D^{-1}hat Hhat D=hat H,$ или $[hat H,hat D]=0.$

Естественно потребовать также сохранения нормы вектора:

Следовательно, оператор преобразования должен быть унитарным:

$hat D^+hat D=hat I,$ или $hat D^{-1}=hat D^+.$

Для приложений представляют интерес унитарные операторы вида

$hat D=e^{ialphahat F},$

где

- эрмитов оператор

т.е. некоторая наблюдаемая;

- вещественный параметр. Условие инвариантности гамильтониана принимает вид

Поэтому наблюдаемая

- интеграл движения (при

)
Пример. Пусть свойства системы инвариантны относительно группы G линейных непрерывных преобразований g координат:

Ввиду скалярности волновой функции ее закон преобразования имеет вид:

$psi'({bf r'})=psi({bf r}),$ или $psi'({bf r})=psi(g^{-1}{bf r})=hat D(g)psi({bf r})$

Линейные операторы

реализуют представление группы G.
Рассмотрим группу трансляций: r'=r+a, где a- постоянный вектор. Тогда

$psi'({bf r})=psi({bf r-a})=[1-{bf a}cdotnabla+frac{1}{2}({bf a}cdotnabla)^2+cdots]psi({bf r})=e^{-{bf a}cdotnabla}psi({bf r}),$

или

$psi'({bf r})={rm exp}left(-frac{i}{hbar}{bf acdothat p}right)psi({bf r}),$

где

- оператор импульса, который оказывается генератором группы трансляций в пространстве волновых функций. Для свободной частицы

коммутирует с гамильтонианом $hat H={bfhat p}^2/2m$ , т.е. является интегралом движения.
Рассмотрим группу вращений SO(3). Нетрудно показать, что волновая функция преобразуется при вращениях по закону:

$psi'({bf r})={rm exp}left( -frac{i}{hbar}varphi{bf ncdot hat L} right) psi({bf r}),$

где

- угол поворота вокруг оси, направление которой задано единичным вектором n;

- оператор момента импульса, или угловой момент. Следовательно, оператор момента - генератор группы вращений. Можно показать (см. ниже п. 9), что для частицы, движущейся в центрально-симметричном поле U(|r|), момент - интеграл движения:

$[hat H,{bfhat L}]=0,; hat H=frac{bf hat p^2}{2m}+U(|{bf r}|)$

Соотношение неопределенностей "время - энергия"

Положим в общей формуле СН

$left lt (Delta A)^2right gt left lt (Delta B)^2right gt ge frac{1}{4} lt C gt ^2,; [hat A,hat B]=ihat C,; hat B=hat H,; frac{partialhat H}{partial t}=0.$

С учетом соотношения

получаем

$left lt (Delta A)^2right gt left lt (Delta E)^2right gt ge frac{hbar^2}{4}left( frac{d lt A gt }{dt}right)^2.$

Введем характерное время изменения наблюдаемой :

$Delta t_A=frac{left lt (Delta A)^2right gt ^{1/2}}{left|frac{d lt A gt }{dt}right|}.$

Тогда получим

$Delta Ecdot Delta t_Age frac{hbar}{2},$

где $Delta E= left lt (Delta E)^2right gt ^{1/2}.$ Следовательно, множество значений

для всевозможных наблюдаемых ограничено снизу. Определим время, за которое в процессе эволюции системы заметно изменяется распределение хотя бы одной из наблюдаемых:

$Delta t=inflimits_{A}^{}Delta t_A.$

. Тогда получаем, что для любого состояния

справедливо соотношение, называемое соотношением неопределенностей "время - энергия":

$Delta Ecdot Delta tgefrac{hbar}{2}.$

Подчеркнем, что здесь

- неопределенность энергии в состоянии

которая от времени не зависит (в силу

).
Качественно СН "время - энергия" может быть получено из анализа эволюции волнового пакета, рассмотренного выше в п. 2: разброс частот в пакете и характерное время его расплывания связаны условием

Учитывая, что

получим

Гармонический осциллятор

Осциллятор в классической механике

Гармоническим осциллятором (ГО) в классической механике называется система, описываемая гамильтонианом (см. выше п. 1)

$H=frac{1}{2m}p_x^2+frac{momega^2}{2}x^2.$

Уравнение движения

имеет общее решение

где A и

- произвольные постоянные. Оно описывает гармонические колебания частицы около положения равновесия x=0. Энергия осциллятора - интеграл движения,

$E=frac{1}{2}momega^2 A^2={rm const},$

и принимает произвольные неотрицательные значения.
К ГО сводится задача о движении частицы в потенциальном поле U(q) при условии, что потенциал имеет локальный минимум в точке q=q₀, и в ее малой окрестности справедливо разложение:

U(q)=U(q₀)+1/2 U''(q₀)(q-q₀)²+...

Введя новую координату x=q-q₀ и обозначив

получим потенциал ГО при условии, что энергия частицы E близка к U(q₀), так что можно пренебречь высшими членами разложения по x. При этом всегда можно положить U(q₀)=0 ввиду произвола выбора начала отсчета энергии.
Заметим, что ГО - простая модель, описывающая приближенно колебания атомов в молекулах, в твердых телах (вблизи узлов кристаллической решетки), колебания поверхности атомных ядер и др. Однако для таких задач классическая теория неприменима.

Стационарные состояния осциллятора

В квантовой механике ГО отвечает оператор Гамильтона

$hat H=frac{1}{2m}hat p_x^2+frac{1}{2}momega^2hat x^2,; [hat x,hat p_x]=ihbar.$

Рассмотрим стационарные состояния ГО, используя координатное представление

$psi(t,x)={rm exp}left(-frac{i}{hbar}Etright)varphi(x).$

Стационарное уравнение Шредингера

принимает вид:

$frac{d^2varphi}{dx^2}+frac{2m}{hbar^2}left(E-frac{m}{2}omega^2 x^2right)varphi=0.$

Удобно ввести безразмерные координату и параметр:

$xi=frac{x}{x_0},; lambda=frac{2E}{hbaromega},$

где характерная длина

$x_0=sqrt{frac{hbar}{momega}}.$

Тогда получим уравнение

Найдем сначала асимптотику решения

при

$varphi''-xi^2varphicong 0,; varphicongvarphi_infty=C_1 e^{-xi^2/2}+C_2 e^{xi^2/2}.$

Потребуем выполнения условия

что соответствует финитному движению в классической механике. Тогда решение УШ должно иметь вид:

$varphi= e^{-xi^2/2}v(xi),$

где v - полином конечного порядка по

Для

получаем уравнение

Ищем его решение в виде степенного ряда:

$v=sumlimits_{k=0}^{infty}c_kxi^k.$

Подставив ряд в уравнение и сделав очевидные замены индекса суммирования, находим:

$sumlimits_{k=0}^{infty}xi^k[(k+2)(k+1)c_{k+2}+(lambda-1-2k)c_k]=0.$

Отсюда следует рекуррентное соотношение для коэффициентов ряда:

$c_{k+2}=frac{2k+1-lambda}{(k+1)(k+2)}c_k.$

Ряд превращается в полином только при

Следовательно, энергия осциллятора

должны быть квантованной:

$E_n=hbaromegaleft(1+frac{1}{2}right).$

Заметим, что

$E_nge E_0=frac{1}{2}hbaromega gt 0.$

В классической же теории E_min=0. Напомним (см. п. 1), что согласно первоначальному постулату квантования Планка

Рассмотрим собственные функции

Полученное выше рекуррентное соотношение связывает коэффициенты при степенях

одинаковой четности. Это не случайно: гамильтониан ГО - четная функция x,

Поэтому

принадлежат одному и тому же собственному значению E_n. Но в одномерном случае вырождение, как известно, отсутствует, т.е.

C=const. Учитывая, что произвольная функция всегда может быть представлена в виде суммы четной и нечетной функций:

$varphi(x)=varphi_+(x)+varphi_-(x),; varphi_pm(x)=frac{1}{2}[varphi(x)pm varphi(x)]=pmvarphi_pm(-x),$

получаем, что собственные функции должны быть определенной четности. Формально это означает существование оператора четности

коммутирующего с гамильтонианом,

Его собственными функциями являются

В рассматриваемом случае ГО из рекуррентных соотношений следует, что четность

совпадает с четностью n:

Полагая

c₁=0 получим четные собственные функции, а при c₀=0,

- нечетные.
Нормированные волновые функции стационарных состояний ГО имеют вид (их вывод мы дадим ниже простым алгебраическим методом):

$varphi_n(x)=(sqrt{pi}2^n n! x_0)^{-1/2}H_n(xi) e^{-xi^2/2}.$

Здесь введены полиномы Эрмита:

$H_n(xi)=(-1)^n e^{xi^2}frac{d^n}{dxi^n}e^{-xi^2}.$

В частности,

Покажем теперь, что ненулевое минимальное собственное значение энергии осциллятора E₀ прямо следует из соотношения неопределенностей. В стационарных состояниях <x>=0, <p_x>=0 в силу определенной четности волновых функций, и СН принимает вид

$left lt x^2right gt left lt p_x^2right gt gefrac{hbar^2}{4}.$

Поэтому для энергии в таких состояниях имеем:

$E= lt hat H gt =frac{1}{2m}left lt p_x^2right gt +frac{1}{2}momega^2 left lt x^2right gt ge frac{hbar^2}{8mleft lt x^2right gt }+frac{1}{2}momega^2left lt x^2right gt equiv fleft(left lt x^2right gt right).$

Условие минимума функции f дает:

$f'=-frac{hbar^2}{8mleft lt x^2right gt }+frac{1}{2}momega^2=0,; left lt x^2right gt _{min}= frac{hbar}{2momega}=frac{1}{2}x_0^2.$

В результате

$E_{min}=E_0=frac{1}{2}hbaromega,$

как и должно быть.
Как уже отмечалось, ГО моделирует колебания атомов в кристаллической решетке. Фундаментальный вывод квантовой механики о том, что в основном состоянии осциллятора энергия

был подтвержден в экспериментах по рассеянию рентгеновского излучения в кристаллах при низких температурах (R.W. James, E.M. Firth, 1927). В отсутствие колебаний решетки (как это следует из классической теории в пределе нулевой температуры) рассеяния бы не было, но эксперимент его обнаружил. При этом экстраполяция результатов к нулевой температуре показала, что интенсивность рассеяния имеет конечный предел.

Алгебра гармонического осциллятора. Метод факторизации

Покажем, что спектр и собственные векторы гамильтониана ГО можно найти, используя только алгебру наблюдаемых и общие свойства гильбертова пространства состояний.
Запишем гамильтониан в виде

$hat H=frac{hbaromega}{2}hat h,; hat h=left(frac{hat p_x}{p_0}right)^2+left( frac{hat x}{x_0}right)^2,$

где, как и выше, $x_0=sqrt{hbar/momega},$ a $p_0=hbar/x_0=sqrt{hbar momega}.$ Нормированный (безразмерный) гамильтониан

представим в факторизованном виде:

$hat h= left(frac{hat x}{x_0}-ifrac{hat p_x}{p_0}right)left(frac{hat x}{x_0} +ifrac{hat p_x}{p_0}right)-ileft[frac{hat x}{x_0},frac{hat p_x}{p_0}right].$

Введем эрмитово сопряженные друг другу операторы

$hat a=frac{1}{sqrt{2}}left(frac{hat x}{x_0}+ifrac{hat p_x}{p_0}right),; hat a^+=frac{1}{sqrt{2}}left(frac{hat x}{x_0}-ifrac{hat p_x}{p_0}right),; [hat a,hat a^+]=1,$

где учтен фундаментальный коммутатор

и равенство

В результате получаем факторизованное представление гамильтониана ГО:

$hat H=hbaromegaleft(hat a^+hat a+frac{1}{2}right).$

Задача свелась к нахождению спектра

и нормированных собственных векторов (СВ)

эрмитова оператора

Итак,

Отсюда получаем:

$lambda=(varphi_lambda,hat Nvarphi_lambda)=(hat avarphi_lambda, hat avarphi_lambda)=|hat avarphi_lambda|^2ge 0,; |hat avarphi_lambda|=sqrt{lambda}.$

Следовательно, спектр энергии ГО ограничен снизу:

$E_lambda=hbaromegaleft(lambda+frac{1}{2}right)ge frac{1}{2}hbaromega.$

Итак,

причем наименьшему собственному значению

отвечает вектор

удовлетворяющий уравнению

Далее заметим, что

или

Используя этот коммутатор, получаем

откуда

Следовательно,

$hat avarphi_lambda=C_lambda^{(-)}varphi_{lambda-1},; C_lambda^{(-)}|hat avarphi_lambda |=sqrt{lambda}.$

Получаем нормированный СВ

$varphi_{lambda-1}=frac{1}{sqrt{lambda}}hat avarphi_lambda.$

Подействовав k раз оператором

на вектор

получим нормированный СВ

$varphi_{lambda-k}=[lambda(lambda-1)cdots (lambda-k)]^{1/2}varphi_lambda.$

Мы уже доказали, что

Поэтому процедура должна оборваться при достижении СВ

. Это возможно только при

В результате мы получили спектр энергии ГО:

$E_n=hbaromegaleft(n+frac{1}{2}right).$

Покажем теперь, что все СВ могут быть построены по вектору

Воспользуемся коммутатором

Имеем

Значит,

$hat a^+varphi_n=C_n^{(+)}varphi_{n+1}.$

Далее,

$|hat a^+varphi_n|^2=(varphi_n, hat ahat a^+varphi_n)=(varphi_n,(1+hat N)varphi_n) =n+1,; C_n^{(+)}=sqrt{n+1}.$

В итоге получим:

$varphi_n=frac{(hat a^+)^n}{sqrt{n!}}varphi_0,; |varphi_n|=1;; hat a^+varphi_n=sqrt{n+1}varphi_{n+1},; hat avarphi_n=sqrt{n}varphi_{n-1}, ; hat avarphi_0=0.$

Применим полученные формулы в координатном представлении для вывода явных выражений для волновых функций ГО. Имеем

$left(begin{array}{c}hat ahat a^+end{array}right)=frac{1}{sqrt{2}}left(frac{hat x}{x_0}pm ifrac{hat p_x}{p_0}right)=frac{1}{sqrt{2}}left(xipmfrac{partial}{partialxi}right).$

Для определения волновой функции основного состояния получаем простое уравнение

$left(xi+frac{d}{dxi}right)varphi_0=0.$

Его решение

$varphi_0=C_0 e^{-xi^2/2}.$

Нормировочный коэффициент определяем из условия

$|varphi_0|^2=intlimits_{-infty}^{infty}dx|varphi_0|^2=|C_0|^2 x_0intlimits_{-infty}^{infty}dxi e^{-xi^2}=1,$

откуда (выбирая соответствующий фазовый множитель)

$C_0=left(x_0sqrt{pi}right)^{-1/2}.$

Волновую функцию состояния с номером n>0 находим по общей формуле:

$varphi_n=frac{(hat a^+)^n}{sqrt{n!}}varphi_0=frac{C_0}{sqrt{2^n n!}}left(xi-frac{d}{dxi}right)^n e^{-xi^2/2}.$

Далее воспользуемся легко проверяемым операторным тождеством:

$xi-frac{d}{dxi}=-e^{xi^2/2}frac{d}{dxi}e^{-xi^2/2},$

откуда

$left(xi-frac{d}{dxi}right)^n=(-1)^n e^{xi^2/2}frac{d^n}{dxi^n}e^{-xi^2/2}.$

В результате получим волновые функции осциллятора в окончательном виде:

$varphi_n=C_n H_n (xi)e^{-xi^2/2},; C_n=left(x_0sqrt{pi} 2^n n!right)^{-1/2},; H_n(xi)=(-1)^n e^{xi^2}frac{d^n}{dxi^n}e^{-xi^2}.$

Когерентные состояния гармонического осциллятора

Состояния, минимизирующие произведение неопределенностей координаты и импульса частицы, подчиняются, как показано в п. 4, уравнению

$left(frac{hbar}{2sigma^2}(hat x-x_0)+i(hat p_x-p_0)right)varphi=0.$

Для осциллятора оно может быть, очевидно, записано в виде:

где

- произвольное комплексное число. Итак, минимизирующие СН состояния описываются собственными векторами оператора

Комплексность собственных значений объясняется неэрмитовостью

Найдем выражение для

в базисе из СВ гамильтониана (энергетическое представление). Имеем

$phi_alpha=sumlimits_{n=0}^{infty}c_nvarphi_n,; hat aphi_alpha =sumlimits_{n=1}^{infty} c_nsqrt{n} varphi_{n-1}=alphasumlimits_{n=0}^{infty}c_n varphi_n,$

откуда следует рекуррентное соотношение для коэффициентов:

$c_{n+1}=frac{alpha}{sqrt{n+1}}c_n,$ и $c_n=frac{alpha^n}{sqrt{n!}}c_0.$

Коэффициент c₀, полагая его действительным, находим из нормировочного условия:

$(phi_alpha,phi_alpha)=1=c_0^2 sumlimits_{n,n'}^{} frac{(alpha^*)^{n'}alpha^n}{sqrt{n'!n!}}(varphi_{n'},varphi_n) =c_0^2sumlimits_{n=0}^{infty}frac{(|alpha|^2)^n}{n!},; c_0=e^{-|alpha|^2/2},$

где учтено условие ортонормированности $(varphi_{n'},varphi_n)=delta_{n'n}.$
Итак,

$phi_alpha=e^{-|alpha|^2/2}sumlimits_{n=0}^{infty} frac{alpha^n}{sqrt{n!}}varphi_n.$

Следовательно, вероятность обнаружить осциллятор в стационарном состоянии с энергией E_n равна

$w_n=|(varphi_n,phi_alpha)|^2=frac{|alpha|^{2n}}{n!} e^{-|alpha|^2}.$

Мы получили известное распределение Пуассона, так что физический смысл параметра

таков:

$|alpha|^2= lt n gt =sumlimits_{n=0}^{infty}nw_n.$

До сих пор мы рассматривали состояние осциллятора

в фиксированный момент времени t=0. Состояние

при t>0 получим очевидной заменой базисных векторов в разложении

$varphi_ntopsi_n={rm exp}left(-frac{i}{hbar}E_n tright) varphi_n.$

Учтя выражения для спектра,

получим закон эволюции во времени минимизирующего состояния:

$phi_alphatochi_alpha = e^{-iomega t/2} phi_{alpha_i},; alpha_iequiv alpha e^{-iomega t}.$

Отсюда следует, что

, как и

, также собственный вектор оператора

Вычислим среднее значение координаты осциллятора в состоянии

, Удобно использовать представление

$hat x=frac{x_0}{sqrt{2}}(hat a+hat a^+).$

Тогда получим

$lt x gt =frac{x_0}{sqrt{2}}(chi_alpha, (hat a+hat a^+) chi_alpha)=frac{x_0}{sqrt{2}}(a_t+a^*_t),$

или, полагая $alpha=|alpha|e^{-itheta}$ ,

$lt x gt =Acos(omega t+theta),; A=sqrt{2}|alpha|x_0.$

Таким образом, среднее значение координаты в состоянии

изменяется по классическому закону
Найдем явный вид

, решая уравнение

в координатном представлении:

$frac{1}{sqrt{2}}left(xi+frac{d}{dxi}right) phi_alpha =alphaphi_alpha,; phi_alpha=C{rm exp}left[- frac{1}{2}(xi-sqrt{2}alpha)^2right].$

В результате получим нормированное решение

$chi_alpha=e^{-iomega t/2}phi_{alpha_t}= (sqrt{pi}x_0)^{-1/2} {rm exp}left[-frac{i}{2} omega t+frac{1}{4}(alpha_t-alpha_t^*)^2 -frac{1}{2} (xi-sqrt{2}alpha_t)^2right],$

представляющее собой нерасплывающийся волновой пакет. Впервые он был построен Шредингером в 1926 г. Координаты в состоянии

распределены по нормальному закону:

$rho(x)=|chi_alpha|^2=frac{1}{sqrt{pi}x_0}{rm exp} left[-frac{1}{x_0^2}(x-Acos(omega t+theta))^2right].$

Центр пакета движется по классическому закону, ширина пакета не зависит от времени:

$left lt (x- lt x gt )^2right gt =frac{1}{2}x_0^2.$

Как уже было показано выше, энергия в пакете распределена по закону Пуассона:

$w(E=E_n)=|(psi_n,chi_alpha)|^2=w_n= frac{ lt n gt ^n}{n!} e^{-left lt nright gt }.$

Независимость распределения от времени обусловлена тем, что гамильтониан осциллятора - интеграл движения. Средняя энергия может быть выражена через амплитуду колебаний около центра пакета $A=sqrt{2}|alpha|x_0$ :

$lt E gt =hbaromegaleft( lt n gt +frac{1}{2}right)=frac{1}{2}(momega^2 A^2+hbaromega).$

Эта формула отличается от классической добавлением в правой части энергии основного состояния осциллятора

(см. выше), которой можно пренебречь только при

(при этом распределение Пуассона переходит, как известно, в нормальное распределение Гаусса).
Заметим, что теоремы Эренфеста для ГО дают классические уравнения движения для средних:

$frac{dleft lt xright gt }{dt}=frac{left lt p_xright gt }{m},; frac{dleft lt p_xright gt }{dt}=-momega^2left lt xright gt ,$

откуда

$frac{d^2left lt xright gt }{dt^2}+omega^2left lt xright gt =0.$

Это объясняется квадратичной зависимостью потенциала ГО от координаты.
Итак, мы построили нерасплывающиеся волновые пакеты

, минимизирующие соотношение неопределенностей "координата - импульс". Они описывают состояния ГО, максимально близкие к классическим. Эти состояния называют когерентными состояниями, так как они используются для описания когерентных свойств электромагнитного излучения в квантовой теории поля (R. Glauber, 1963): можно показать, что свободное электромагнитное поле эквивалентно бесконечному набору независимых гармонических осцилляторов.

Оператор момента импульса

Коммутационные соотношения

Оператор момента импульса частицы определим, используя принцип соответствия, в виде

${bfhat L=hat rtimeshat p}=-ihbar {bf r timesnabla}= left|begin{array}{ccc} {bf e}_x& {bf e}_y& {bf e}_z hat x&hat y&hat z hat p_x&hat p_y&hat p_z end{array}right|.$

Напомним (см. п. 5), что оператор момента естественно определяется как генератор группы вращений в пространстве волновых функций.
На основе коммутаторов (фундаментальных квантовых скобок Пуассона) $[hat x_k, hat p_n]=ihbardelta_{kn}$ получаем

Используя циклическую перестановку индексов, получим еще два соотношения. В итоге:

В тензорной форме:

$[hat L_k,hat L_n]=ihbarvarepsilon_{kns}hat L_s,$

или символически:

Введем оператор квадрата момента

$hat{bf L}=hat L_x^2+hat L_y^2+hat L_z^2.$

Вычислим его коммутатор с компонентами момента:

$[hat L_k,hat{bf L}^2]=sumlimits_{n}^{}(hat L_khat L_n^2-hat L_n^2hat L_k+hat L_nhat L_khat L_n - hat L_nhat L_khat L_n)=sumlimits_{n}^{}([hat L_k,hat L_n]hat L_n+hat L_n[hat L_k,hat L_n])=ihbarvarepsilon_{kns}(hat L_shat L_n+hat L_nhat L_s)equiv 0.$

Итак, квадрат момента коммутирует со всеми компонентами:

$[hat L_k,{bfhat L}^2]=0.$

Этого и следовало ожидать, так как скаляр при поворотах системы координат не изменяется.
Рассмотрим теперь алгебру операторов момента в общем виде, не фиксируя ее представление. Выбирая

в качестве естественной единицы измерения момента и обозначая (безразмерные) компоненты

, получаем коммутационные соотношения в виде:

$[hat J_k,hat J_n]=ivarepsilon_{kns}hat J_s,; [hat J_k,{bfhat J}^2]=0.$

Введем неэрмитовы сопряженные друг другу операторы

Тогда получим коммутаторы:

$[hat J_z,hat J_pm]=pmhat J_pm,; [hat J_+,hat J_-]=2hat J_z,; [{bfhat J}^2,hat J_pm]=[{bfhat J}^2,hat J_z]=0.$

Квадрат момента удобно записать так:

${bf hat J}^2=frac{1}{2}(hat J_+hat J_- + hat J_-hat J_+)+hat J_z^2.$

Отсюда с учетом

находим

$hat J_-hat J_+={bfhat J}^2-hat J_z(hat J_z+1),; hat J_+hat J_-={bfhat J}^2-hat J_z(hat J_z-1).$

Спектр операторов квадрата момента и проекции момента на ось.

В силу $[{bfhat J}^2,hat J_z]=0$ существует общая система собственных векторов этих операторов:

$hat{bf J}^2psi_{lambda m}=lambdapsi_{lambda m},; hat J_zpsi_{lambda m}=mpsi_{lambda m}.$

Покажем, что

Имеем

$lambda=(psi_{lambda m},hat{bf J}^2psi_{lambda m})= sumlimits_{k}^{}(psi_{lambda m},hat J_k^2psi_{lambda m}) = sumlimits_{k}^{}|hat J_kpsi_{lambda m}|^2ge 0,$

где учтена эрмитовость операторов

.
Из полученных выше тождеств для произведений операторов

находим:

$hat J_mp hat J_pmpsi_{lambda m}=[hat{bf J}^2-hat J_z(hat J_zpm 1)]psi_{lambda m}=[lambda-m(mpm 1)]psi_{lambda m}.$

Умножив слева скалярно на $psi_{lambda m}$ обе части этих равенств, получим с учетом

$(psi_{lambda m},hat J_mp hat J_pmpsi_{lambda m})= (hat J_pm psi_{lambda m},hat J_pmpsi_{lambda m})=[lambda-m(mpm 1)](psi_{lambda m},psi_{lambda m}).$

Следовательно,

$|hat J_pmpsi_{lambda m}|^2=[lambda-m(mpm 1)] |psi_{lambda m}|^2.$

В силу неотрицательности нормы вектора имеем:

или

$left.begin{array}{c} m^2+m-lambdale 0, m^2-m-lambdale 0. end{array}right}$

Отсюда

$left.begin{array}{c} m^+_1 le mle m^+_2, m^-_1 le mle m^-_2, end{array}right}$

где

$m_{1,2}^+=-frac{1}{2}mpsqrt{Delta},; m_{1,2}^-=frac{1}{2}mpsqrt{Delta},; Delta=frac{1}{4}+lambdage frac{1}{4}.$

Получаем решение системы неравенств:

$frac{1}{2}-sqrt{Delta}le mle -frac{1}{2}+sqrt{Delta}.$

Обозначим

$j=sqrt{Delta}-frac{1}{2}ge 0.$

Тогда находим:

Далее собственные векторы будем обозначать $psi_{jm}$ . Так как

, то $hat J_pmpsi_{jm}=0$ тогда и только тогда, когда

. С учетом ограничения

приходим к выводу:

$hat J_+psi_{jj}=0,; hat J_-psi_{j,-j}=0.$

Пусть

. Учитывая соотношения

$hat{bf J}^2hat J_+=hat{bf J}^2hat J_+,; hat J_zhat J_+=hat J_+(hat J_z+1),$

находим

$hat{bf J}^2(hat J_+psi_{jm})=j(j+1)(hat J_+psi_{jm}),; hat J_z(hat J_+psi_{jm})=m(m+1)(hat J_+psi_{jm}).$

Следовательно,

$hat J_+psi_{jm}=C^+_{jm}psi_{j,m+1}.$

Аналогично найдем:

$hat J_-psi_{jm}=C^-_{jm}psi_{j,m-1}.$

Выше было получено:

$|hat J_pmpsi_{jm}|=[j(j+1)-m(m+1)]^{1/2}|psi_{jm}|.$

Рассмотрим последовательность векторов

$hat J_+psi_{jm},hat J_+^2psi_{jm},ldots,hat J_+^npsi_{jm},ldots.$

Очевидно, что

$hat J_+^npsi_{jm}sim psi_{j,m+n}$

, причем

Ясно, что существует целое неотрицательное число n₊ такое, что

$hat J_+(hat J_+^{n_+}psi_{jm})=0,$

т.е. m+n₊=j. Итак,

причем существует n₊ собственных векторов операторов $hat{bf J}^2$ и

$hat J_+psi_{jm},ldots,hat J_+^{n_+}psi_{jm},$

отвечающих собственным значениям оператора

, равным

m+1,...,m+n₊=j.

Аналогично получаем для

последовательность векторов

$hat J_-psi_{jm},ldots,hat J_-^{n_-}psi_{jm},$

принадлежащих СЗ

, равным соответственно

m-1,...,m-n_-=-j.

Из условий

следует, что

n₊+n_-=2j=0,1,2,...

Итак, СЗ оператора $hat{bf J}^2$ равны j(j+1), где

j=0,1/2,1,3/2,2,...

СЗ оператора

таковы:

Для общего СВ $psi_{jm}$ операторов $hat{bf J}^2$ и

возможны 2j+1 значений m:

m=-j,-j+1,...,j.

Вернемся к соотношениям

$hat J_+psi_{jm}=C^+_{jm}psi_{j,m+1},; |hat J_+psi_{jm}|=[j(j+1)-m(mpm 1)]^{1/2}|psi_{j,mpm 1}|.$

Выберем $|psi_{jm}|=1$ и фиксируем фазу вектора $psi_{j,m+1}$ так, чтобы $C^+_{jm}$ было действительным неотрицательным числом. Тогда получим

$hat J_+psi_{jm}=[j(j+1)-m(m+1)]^{1/2}psi_{j,m+1}.$

Отсюда с учетом уже полученного соотношения

$hat J_-hat J_+psi_{jm}=[j(j+1)-m(m+1)]psi_{jm}$

находим:

$hat J_-psi_{j,m+1}=[j(j+1)-m(m+1)]^{1/2}psi_{jm}.$

Подведем итоги. Исходя из существования одного вектора $psi_{jm}$ , мы построили всего 2j+1 ортонормированных векторов:

$psi_{j,-j},psi_{j,-j+1},ldots,psi_{jm},ldots,psi_{j,j-1}, psi_{jj};; (psi_{jm'},psi_{jm})=delta_{m'm}.$

Они образуют базис 2j+1-мерного пространства H^(j) , инвариантного относительно действия операторов момента

. Соберем вместе основные полученные соотношения:

$begin{array}{cc} hat{bf J}^2psi_{jm}=j(j+1)psi_{jm},; j=0,1/2,1,3/2,2,ldots; hat J_zpsi_{jm}=mpsi_{jm},; m=-j,-j+1,ldots,j; hat J_pmpsi_{jm}=[j(j+!)-m(mpm 1)]^{1/2}psi_{j,mpm 1}; hat J_+psi_{jj}=hat J_-psi_{j,-j}=0. end{array}$

Исследование свойств момента было основано только на коммутационных соотношениях и эрмитовости операторов момента, а также на неотрицательности нормы векторов состояний. Далее мы рассмотрим конкретные представления алгебры момента.

Орбитальный момент

Оператор орбитального момента частицы определен выше:

В координатном представлении получаем:

${bfhat l}=-ihat {bf r}timesnabla;; hat l_x=-ileft(yfrac{partial}{partial z}-zfrac{partial}{partial y}right),; hat l_y=-ileft(zfrac{partial}{partial x}-xfrac{partial}{partial z}right),; hat l_z=-ileft(xfrac{partial}{partial y}-yfrac{partial}{partial x}right).$

Найдем выражения для компонент момента в сферических координатах, связанных с декартовыми координатами соотношениями:

Вычисляем производные волновой функции

как сложной функции сферических координат:

$begin{array}{l} frac{partialpsi}{partialtheta}=rcosthetaleft( frac{partialpsi}{partial x}cosvarphi+ frac{partialpsi}{partial y}sinvarphiright) - frac{partialpsi}{partial z}rsintheta=zleft( frac{partialpsi}{partial x}frac{x}{rho}+ frac{partialpsi}{partial y}frac{y}{rho}right)- rhofrac{partialpsi}{partial z}; frac{partialpsi}{partialvarphi}=rsinthetaleft( - frac{partialpsi}{partial x}sinvarphi+ frac{partialpsi}{partial y}cosvarphiright)= -yfrac{partialpsi}{partial x}+xfrac{partialpsi}{partial y}= ihat l_xpsi, end{array}$

где $rho=rsintheta=sqrt{x^2+y^2}$ . Умножим первое равенство на

, а второе на $-yz/rho^2;({rm на}; -xz/rho^2)$ и сложим почленно. Получим соответственно:

$zfrac{partialpsi}{partial x}-xfrac{partialpsi}{partial z}=frac{x}{rho}frac{partialpsi}{partialtheta}-frac{yz}{rho^2}frac{partialpsi}{partialvarphi}=ihat l_ypsi,; yfrac{partialpsi}{partial z}-zfrac{partialpsi}{partial y}=-frac{y}{rho}frac{partialpsi}{partialtheta}-frac{xz}{rho^2}frac{partialpsi}{partialvarphi}=ihat l_xpsi.$

В результате находим искомые выражения:

$hat l_x=ileft(sinvarphifrac{partial}{partialtheta} +cosvarphi,{rm ctg},thetafrac{partial}{partialvarphi} right),; hat l_y=ileft(-cosvarphifrac{partial}{partialtheta} +sinvarphi,{rm ctg},thetafrac{partial}{partialvarphi} right),; hat l_z=-ifrac{partial}{partialvarphi}.$

Кроме того,

$hat l_pm=e^{pm i varphi}left( pmfrac{partial}{partialtheta} + i,{rm ctg},thetafrac{partial}{partialvarphi}right).$

Используя известное выражение для квадрата момента (см. выше)

${bfhat l}^2=hat l_-hat l_+ +hat l_z(hat l_z+1),$

нетрудно отсюда получить для него представление в сферических координатах:

${bfhat l}^2=-left[ frac{1}{sintheta} frac{partial}{partialtheta} left(sinthetafrac{partial}{partialtheta} right) + frac{1}{sin^2theta} frac{partial^2}{partialvarphi^2}right]equiv =-Lambda,$

где

- угловая часть оператора Лапласа.
Найдем общие собственные функции операторов ${bfhat l}^2 ; hat l_z$ :

${bfhat l}^2psi_{tm}=ell(ell+1)psi_{tm},; hat l_zpsi_{tm}=mpsi_{tm},$

Решаем второе уравнение:

$left(-ifrac{partial}{partialvarphi}-mright)psi_{tm}=0,; psi_{tm}(theta,varphi)=f_{tm}(theta)e^{imvarphi}.$

Потребуем однозначности функции:

Тогда $e^{2pi mi}=1$ , и собственные значения

Замечание. Требование однозначности волновой функции слишком жесткое (достаточно однозначности модуля функции), и его можно снять (см. ниже).
Из общей теории (см. выше) известно, что

. Поэтому для орбитального момента имеем только целые значения

Рассмотрим собственную функцию при

$psi_{ellell}=f_{ell}e^{iellvarphi}.$

Она удовлетворяет уравнению

$hat l_+psi_{ellell}=0,$

или

$e^{ivarphi}left( frac{partial}{partialtheta} +i,{rm ctg },theta frac{partial}{partialvarphi}right) f_{ell}e^{iellvarphi}=0 .$

Для функции

после замены переменной

получаем уравнение, которое легко решается:

$left(frac{d}{dx}-frac{ell}{z}right)f_ell=0,; f_ell=cx^ell.$

Итак, для каждого целого

существует единственная собственная функция

$psi_{ellell}(theta,varphi)=c_ell sin^ell theta e^{iellvarphi}.$

Следовательно, общий спектр операторов ${bf hat l}^2,; hat l_x$ в целом невырожден: каждой паре собственных значений

отвечает одна собственная функция.
Нормируем $psi_{tm}$ на единицу и фиксируем фазу. Тогда получим ортонормированную систему функций $psi_{tm}equiv Y^m_ell(theta,varphi)$ :

$Y^m_ell(theta,varphi)(Y^{m'}_ell, Y^m_ell)=intlimits_{0}^{2pi}dvarphiintlimits_{0}^{pi}dthetasintheta {Y^{m'}_ell}^*(theta,varphi) Y^m_ell(theta,varphi)=delta_{m'm}delta_{ell'ell}.$

Условие полноты системы:

$sumlimits_{ell=0}^{infty}sumlimits_{m=-ell}^{ell} Y^m_ell(theta,varphi){Y^m_ell}^*(theta',varphi')= delta(costheta -costheta')delta(varphi-varphi').$

Далее требуем выполнения условий (см. выше):

$hat l_pm Y^m_ell=[ell(ell+1)-m(mpm 1)]^{1/2}Y^{mpm 1}_ell.$

Тем самым определены относительные фазы

функций, отвечающих заданному

. Фиксируем фазу одной из функций. Мы выберем

так, чтобы

было действительным положительным числом.
Произвольную функцию

получаем из $Y^{pm ell}_ell$ многократным действием операторов

$Y^m_ell=left[frac{(ell+m)!}{(2ell)!(ell-m)!}right]^{1/2} hat l^{ell-m}_-Y^ell_ell=left[frac{(ell-m)!} {(2ell)!(ell+m)!} right]^{1/2}hat l^{ell+m}_-Y^{-ell}_ell.$

Далее используем явный вид

$hat l_pm e^{imvarphi}f(theta)=e^{i(mpm 1)varphi}left(pm frac{d}{dtheta}-mfrac{costheta}{sin theta}right)f(theta) =mp e^{i(mpm 1)varphi}sin^{1pm m}thetafrac{d}{dcostheta}sin^{mp m}theta f(theta).$

Отсюда

$hat l^n_pm e^{imvarphi}f(theta)=(mp 1)^n e^{i(mpm n)varphi}sin^{npm m}thetafrac{d^n}{d(costheta)^n}(sin^{mp m}theta f(theta))$

Имеем функцию (см. выше)

$Y^ell_ell(theta,varphi)=c_ellsin^elltheta e^{iellvarphi}.$

Нормируя ее условием

, получим

$|c_ell|=frac{1}{2^ell ell!}left[ frac{(2ell+1)!}{4pi}right]^{1/2}.$

Теперь находим

$Y^m_ell=c_ellleft[frac{(ell+m)!}{(2ell)!(ell-m)!}right]^{1/2}e^{imvarphi}sin^{-m}thetafrac{d^{ell-m}}{d(costheta)^{ell-m}}sin^{2ell}theta.$

При

отсюда следует

$Y^{-ell}_ell=(-1)^ell c_ell e^{-iellvarphi}sin^elltheta.$

Тогда находим эквивалентное выражение для собственных функций:

$Y^m_ell=(-1)^m c_ellleft[frac{(ell-m)!}{(2ell)!(ell+m)!}right]^{1/2}e^{imvarphi}sin^{m}thetafrac{d^{ell+m}}{d(costheta)^{ell+m}}sin^{2ell}theta.$

В частности, при m=0 получаем:

$Y_ell^0=frac{c_ell}{sqrt{(2ell)!}}frac{d_ell}{d(costheta)^ell}(1-cos^2theta)^ell.$

Введем полиномы Лежандра

$P_ell(x)=frac{1}{2^ell ell!}frac{d^ell}{dx^ell}(x^2-1)^ell,; P_ell(1)=1.$

Отсюда и из введенного выше условия фиксации фазы функции

находим нормировочный коэффициент

Определим функции Лежандра в виде:

$P_ell^m=(1-x^2)^{m/2}frac{d^m}{dx^m}P_ell(x)=frac{1}{2^ell ell!}(1-x^2)^{m/2}frac{d^{ell+m}}{dx^{ell+m}}(x^2-1)^ell,$

где

. Тогда окончательно получим:

$Y^m_ell(theta,varphi)=(-1)^{(m+|m|)/2} left[ frac{2ell+1}{4pi}cdotfrac{(ell-|m|)!}{(ell+|m|)!}right]^{1/2}P_ell^{|m|}(costheta)e^{imvarphi}.$

Отсюда находим соотношение между функциями $Y_ell^{pm m}$ :

$Y_ell^{-m}(theta,varphi)=(-1)^m {Y^m_ell}^*(theta,varphi).$

В математической литературе

называются сферическими функциями.
Рассмотрим их преобразование при дискретном преобразовании координат - пространственной инверсии

, отвечающей переходу от правой системы координат к левой:

Из общего выражения для сферических функций сразу следует закон преобразования:

Следовательно,

- собственные функции оператора четности

, принадлежащие собственному значению +1(-1) при четном (нечетном)

.
Общая структура сферических функций такова:

$Y^m_ell=$ {it произведение функции} $e^{imvarphi} sin^{|m|}theta${it четности}$(-1)^{|m|}$ {it и полинома по } $costheta$ {it степени}$ell-|m|$ {it и четности}$(-1)^{ell-|m|}.$

Приведем несколько частных значений:

$Y_0^0=frac{1}{sqrt{4pi}};; Y_1^0=sqrt{frac{3}{4pi}}costheta,; Y_1^{pm 1}=mp sqrt{frac{3}{8pi}}sintheta e^{pm i varphi};; Y_ell^0=sqrt{frac{2ell+1}{4pi}}P_ell(costheta);; Y_ell^ell=(-1)^ellleft[frac{2ell+1}{4pi}cdotfrac{(2ell)!}{2^{2ell}(ell!)^2}right]^{1/2}sin^elltheta e^{iellvarphi}.$

Замечание. Сферические функции связаны с гармоническими полиномами степени

по x,y,z соотношением

$h_ell^m({bf r})=r^ell Y^m_ell(theta,varphi).$

При заданном

имеем

линейно независимых полиномов. Как известно, гармоническая функция по определению удовлетворяет уравнению Лапласа:

В нашем случае это легко проверяется с использованием выражения оператора Лапласа через ${bfhat l}^2$ , которое выводится ниже (см. п. 9):

$nabla^2=frac{1}{r}frac{partial^2}{partial r^2}r-frac{{bfhat l}^2}{r^2}.$

Приведем пример. Пусть

. Тогда получаем три гармонических полинома h₁^m=rY₁^m,

$h_1^0=sqrt{frac{3}{4pi}}z,; h_1^{pm 1}=mpsqrt{frac{3}{4pi}}frac{xpm iy}{sqrt{2}}.$

Сферические функции

реализуют неприводимое

-мерное представление группы вращений SO(3), образуя базис в пространстве функций, заданных на сфере единичного радиуса.
Покажем теперь, что целочисленность

следует из более слабого требования, чем однозначность волновой функции. В общей теории момента фундаментальную роль играют соотношения (см. выше)

$hat J_pm psi_{jm}simpsi_{j,mpm 1};; hat J_+ psi_{jj}=0,; hat J_- psi_{j,-j}=0.$

Отсюда следует

$hat J^{2j+1}_- psi_{jj}=0.$

В рассматриваемом случае орбитального момента получаем

$hat l^{2ell+1}_-Y_ell^ell=0.$

Покажем, что это соотношение не выполняется, если

- четное целое число. Для этого удобно использовать декартовы координаты, в которых имеем:

$hat l_-=hat l_x-ihat l_y=yhat p_z-zhat p_y-i(zhat p_x-xhat p_z)=(x-iy)partial_z-z(partial_x-ipartial_y);; Y_ell^ell= c_ell(e^{ivarphi}sintheta)^ell=frac{c_ell}{r^ell}(x+iy)^ell.$

Заметим, что для произвольной функции f(r), $r=sqrt{x^2+y^2+z^2},$ имеем

. Далее сделаем комплексную замену переменных:

В результате приходим к соотношению

$(vpartial_z-2zpartial_u)^{2n}u^{n-1/2}=0.$

Оно должно выполняться тождественно, что невозможно при целом

. Следовательно,

- целое число. Более подробное рассмотрение показывает, что для полуцелых

операторы момента

оказываются неэрмитовыми, т.е. не могут быть наблюдаемыми.

Основы квантовой механики.

А.В. Борисов (Физический факультет МГУ)
Физический факультет МГУ, 1998 г.

Содержание

Спин. уравнение паули

Оператор спина

Эксперимент показывает (см. ниже), что электрон, наряду с орбитальным моментом, имеет собственный момент импульса - спин (от англ. spin), не связанный с его движением в пространстве. Проекция этого момента на заданное направление может принимать только два значения

. В общей теории момента (см. п. 7) этому отвечает квантовое число j=1/2.
Таким образом, электрон обладает 4 степенями свободы, и его волновая функция

, где дискретная переменная, отвечающая проекции спина на ось z (выбор ее, конечно, условен),

. Иначе говоря, состояние частицы описывается упорядоченной парой функций:

$psi=left(begin{array}{l} psi_1({bf r}) psi_2({bf r}) end{array}right)=left(begin{array}{l} psi_({bf r},zeta=+1/2) psi_({bf r},zeta=-1/2) end{array}right).$

Формально это означает, что от пространства квадратично интегрируемых волновых функций H=L²(R³) мы переходим к прямому произведению

${bf H}_S=L^2({bf R}^3)otimes C^2,$

где C² - двумерное комплексное пространство.
Наблюдаемой

в H отвечает в H_S наблюдаемая

, а

в C² соответствует

в H_S. В пространстве существуют, конечно, и наблюдаемые более общего вида, например, суммы и произведения указанных. В дальнейшем единичные операторы

, как правило, мы будем опускать.
Скалярное произведение в H_S определяется в виде

Введем векторный оператор спина

$hat{bf S}=frac{hbar}{2}{bf sigma}, ; {bf sigma}=(sigma_1,sigma_2,sigma_3).$

Его компоненты

$hat S_k=frac{hbar}{2}sigma_k$

имеют только два собственных значения

и удовлетворяют коммутационным соотношениям для операторов момента:

$[hat S_k,hat S_n]=ihbarvarepsilon_{knl}hat S_n.$

Отсюда следует, что безразмерные эрмитовы 2x2-матрицы

должны удовлетворять условиям

$sigma_k^2=I,; [sigma_k, sigma_n]equiv sigma_ksigma_n-sigma_nsigma_k=2ivarepsilon_{knl}sigma_l,$

где I - единичная матрица. Еще одно условие мы получим из требования, чтобы проекция спина на любое направление, задаваемое единичным вектором ,

$hbar S_{bf n}=frac{hbar}{2}{bf ncdot sigma},$

также имела только два СЗ

. Это значит, что

$({bf ncdotsigma})^2=I=n_ksigma_k n_lsigma_lequiv frac{1}{2}n_k n_l(sigma_ksigma_l+sigma_lsigma_k).$

В силу произвольности направления n матрицы

должны удовлетворять соотношению

${sigma_k,sigma_k}equiv sigma_ksigma_n+sigma_nsigma_k=2delta_{kn}.$

Указанные три условия эквиваленты одному:

$sigma_ksigma_n=delta_{kn}I+ivarepsilon_{kns}sigma_s,$

т.е.

и цикл. пер.
Квадрат спина

$hat{bf s}^2=sumlimits_{k}^{}hat S_k^2=hbar^2s(s+1)I,; s=1/2.$

Это и означает, что спин электрона равен

. Заметим, кстати, что операторы

удовлетворяют условию

которое следует из антикоммутативности матриц

.
Стандартный выбор матриц

таков:

$sigma_1=begin{array}{ll} 0&11&0end{array},; sigma_2=begin{array}{ll} 0&-ii&0end{array},; sigma_3=begin{array}{ll} 1&00&-1end{array}.$

Они называются матрицами Паули (W. Pauli).
Явные выражения для операторов

можно получить из общих формул для матричных элементов операторов момента (см. п. 7):

$(J_pm)_{m'm}equiv (psi_{jm}, hat J_pm psi_{jm})=[j(j+1)-m(m+1)]^{1/2}delta_{m',mpm 1},; (J_3)_{m'm}=mdelta_{m'm}.$

Положив здесь

, получим уже известные 2x2-матрицы (нумеруя соответствующим образом строки и столбцы).
Произвольная наблюдаемая в C² может быть представлена в виде разложения по 4 линейно независимым базисным эрмитовым матрицам

.
Общие собственные векторы операторов

$hat {bf S}^2=frac{3}{4}hbar^2 I$ и $hat S_z=frac{hbar}{2}sigma_3.$

- диагональных матриц - имеют вид

$psi_{zeta=1/2}=begin{array}{l} psi_1 0end{array},; psi_{zeta=-1/2}=begin{array}{l} 0 psi_2end{array},$

где $psi_{1/2}$ - произвольные функции из L²(R³). Из разложения произвольного вектора состояния в H_S,

$psiequivbegin{array}{l} psi_1 psi_2end{array}=psi_{zeta=1/2}=begin{array}{l} psi_1 0end{array}+begin{array}{l} 0 psi_2end{array},$

следует, что вероятность обнаружить при измерении в состоянии

проекцию спина

$w(zeta=pm 1/2)=|(psi_{zeta=pm 1/2},psi)|^2=int d^3 x|psi_{1,2}|^2.$

В пространстве C² волновая функция преобразуется по закону

$psi'=Upsi,$ или $psi'_k=U_{kn}psi_n.$

Сохранение скалярного произведения,

, приводит к унитарности матриц преобразования:

U⁺U=I.

Следовательно,

det U⁺det U=|det U|²=1.

Поэтому произвольную унитарную матрицу можно представить в виде

$U=e^{ialpha}V,$

где V - унитарная матрица с detV=1,

- произвольное действительное число.
Учитывая, что нормированный вектор состояния определен с точностью до фазового преобразования $psito psi'=e^{ialpha}psi$ , мы всегда можем ограничиться преобразованиями U с единичным определителем (унимодулярными преобразованиями):

detU=1.

Унитарные унимодулярные преобразования в двумерном пространстве C² образуют, как известно, группу SU(2). Эта группа связана с группой вращений трехмерного евклидова пространства SO(3) следующим образом. Рассмотрим множество эрмитовых бесследовых матриц вида:

$X={bf sigmacdot r},; X^+=X,; {rm tr},X=0,$

где r - действительный трехмерный вектор. Представление группы SU(2) на множестве этих матриц задано так:

$X^+=UXU^+,$ или ${bf sigmacdot r}=U{bf sigmacdot r}U^+.$

Из перестановочных соотношений для матриц Паули

следует, что

$frac{1}{2}{rm tr}(sigma_ksigma_n)=delta_{kn}.$

Отсюда и из закона преобразования матриц X находим

$frac{1}{2}{rm tr}(sigma_ksigma_n x'_n)=x'_k=frac{1}{2}{rm tr}(sigma_k Usigma_l x_l U^+)equiv R_{kl}x_l.$

Мы получили преобразование в евклидовом пространстве:

r'=Rr,

где 3x3-матрица R имеет матричные элементы

$R_{kl}=frac{1}{2}{rm tr}(sigma_k Usigma_nU^+).$

Используя свойства матриц

и U, нетрудно показать, что R - действительная ортогональная унимодулярная матрица:

R^*=R, R^TR=I, det R=1,

т.е. отвечает вращению евклидова пространства:

. Матрица

может быть при этом параметризована в виде:

$U={rm exp}left(-frac{i}{2}theta{bf ncdotsigma}right)=Icosfrac{theta}{2}-i({bf ncdotsigma})sinfrac{theta}{2},$

где

- угол поворота вокруг оси, заданной единичным вектором n. Здесь учтены легко проверяемые соотношения:

$({bf ncdotsigma})^{2k}=I,; ({bf ncdotsigma})^{2k+1}={bf ncdotsigma}.$

Мы видим, что матрицы U осуществляют двузначное представление группы вращений SO(3):

Волновая функция электрона в пространстве H_S преобразуется при вращении по закону:

$psi'({bf r})=Upsi(R^{-1}{bf r})={rm exp}left(-frac{i}{hbar}theta{bf ncdothat J}right)psi({bf r}),$

где введен оператор полного момента импульса

${bfhat J=hat L+hat S}=-ihbar {bf r}timesnablaotimeshat I+hat Iotimesfrac{hbar}{2}{bfsigma}$

Уравнение Шредингера для частицы во внешнем электромагнитном поле. Магнитный момент

Рассмотрим движение электрона во внешнем электромагнитном поле, заданном 4-потенциалом

. По принципу соответствия определим гамильтониан (нерелятивистского) электрона (массу его будем обозначать m_e, чтобы не путать с квантовым числом m для проекции момента) в виде:

$hat H=frac{1}{2m_e}left(hat {bf p} - frac{e}{c}{bf A}right)^2+ePhi$

. Оператор

$hat {bf P}={bfhat p}-frac{e}{c}{bf A}$

называют кинетическим импульсом (в классической механике он выражается через скорость частицы: P=m_ev) в отличие от канонического импульса

.
Пусть задано постоянное однородное магнитное поле

, калибровку потенциала которого выберем в виде

${bf A}=frac{1}{2}{bf Btimes r},; nablacdot{bf A}=0.$

Тогда, преобразуя квадрат кинетического импульса

$hat {bf P}^2={bfhat p}^2-frac{e}{c}({bf Acdothat p+hat pcdot A})+frac{e^2}{c^2}{bf A}^2$

с учетом

${bfhat pcdot A}psi=({bf Acdothat p})psi-ihbar(nablacdot{bf A})psi,; {bf Acdothat p}=frac{1}{2}{bf B(rtimeshat p}),$

получим гамильтониан электрона в постоянном магнитном поле и произвольном электрическом поле

$hat H=frac{{bf hat p}^2}{2m_e}+ePhi-frac{e}{2m_ec}{bf Bcdothat L}+frac{e^2}{8m_ec^2}({bf Btimes r})^2.$

Третье слагаемое в гамильтониане описывает взаимодействие орбитального магнитного момента M электрона с магнитным полем:

$hat U_L=-{bf hat Mcdot B},; {bfhat M}=frac{e}{2m_e c}{bfhat L}.$

Коэффициент пропорциональности между магнитным моментом и моментом импульса называется гиромагнитным отношением

g_L=e/2m_ec.

Взаимодействие

имеет, очевидно, классический аналог, следующий из классической функции Гамильтона частицы. В общем случае протяженной заряженной системы, характеризуемой плотностью электрического тока j(t,r), энергия ее взаимодействия с постоянным магнитным полем A=Bxr/2 в рамках классической электродинамики имеет вид (см. первую часть курса):

$U_c=-frac{1}{c}int d^3 x{bf jcdot A}=-{bf Mcdot B}.$

Здесь магнитный момент системы

${bf M}=frac{1}{2c}int d^3 x{bf rtimes j}.$

Для системы N точечных заряженных частиц имеем плотность тока в виде

${bf j}(t,{bf r})=sumlimits_{a=1}^{N}e_a {bf v_a}delta({bf r-r_a},$

и магнитный момент

${bf M}=sumlimits_{a}^{}frac{e_a}{2m_a c}{bf r_atimes p_a}.$

В случае, когда все частицы имеют одинаковое отношение заряда к массе, e_a/m_a=e/m_e, получим пропорциональность магнитного и орбитального моментов:

${bf M}=frac{e}{2m_e c}{bf L},; {bf L}=sumlimits_{a}^{}{bf r_a}times{bf p_a}.$

Вычислим магнитный момент

равномерно заряженного по объему шарика радиуса a, вращающегося с постоянной угловой скоростью ${bf omega}=omega{bf e_z}$ вокруг диаметра. Имеем для плотности заряда и тока

$rho=frac{3e}{4pi a^3},; {bf j}=rho {bf v},; {bf v=omegatimes r},$

где e - полный заряд шарика. Очевидно, что магнитный момент

. Тогда получаем

${bfmu}=frac{rho}{2c}int d^3 x{bf rtimes(omegatimes r)}={bf omega}frac{rho}{2c}intlimits_{0}^{2pi}dvarphiintlimits_{0}^{pi}dtheta sinthetaintlimits_{0}^{a}drr^2(x^2+y^2)=frac{ea^2}{5c}{bfomega}.$

При этом магнитный момент пропорционален собственному моменту импульса L_S (в системе, где центр шарика массы m_e покоится):

${bf mu}=frac{e}{2m_e c}{bf L_S},; {bf L_S}=rho_mint d^3 x{bf rtimes v},; rho_m=frac{3m_e}{4pi a^3}.$

Атом в магнитном поле

Для электрона в атоме электростатическое взаимодействие значительно сильнее взаимодействия с магнитными полями, достижимыми в лабораторных условиях. Поэтому квадратичным по напряженности поля слагаемым в гамильтониане можно пренебречь:

$hat H=hat H_0-{bfhat Mcdot B},; hat H_0=frac{{bfhat p}^2}{2m_e}+ePhi, ; {bfhat M}=g_L {bfhat L}.$

Пусть магнитное поле направлено по оси z: B=Be_z. Учтем сферическую симметрию электростатического потенциала,

, рассматривая простую модель атома щелочного металла (вспомним школьную химию): один валентный электрон движется в некотором центральном поле, создаваемом кулоновским взаимодействием с ядром и распределенным по объему атома зарядом остальных электронов. Тогда операторы $hat H, hat{bf L}^2, hat L_z$ образуют полный набор коммутирующих операторов, т.е. имеют общую систему собственных функций $psi_{nlm}$ :

$(hat H-E_{nlm}) psi_{nlm}=0,; [hat{bf L}^2-hbar^2ell(ell+1)]psi_{nlm}=0,; (hat L_z-hbar m)psi_{nlm}=0.$

Здесь собственные значения энергии имеет вид

$E_{nlm}=E^0_{ln}-mfrac{ehbar}{2m_e c}B,; m=-ell,-ell+1,ldots,ell.$

Они связаны с СЗ E_nl⁰ гамильтониана

(в отсутствие магнитного поля, B=0), имеющим, очевидно, те же собственные функции, что и

$(hat H_0-E_{nl}^0)psi_{nlm}=0.$

Мы видим, что возникла естественная единица измерения магнитного момента, называемая магнетоном Бора:

$mu_B=frac{|e|hbar}{2m_e c},$

где заряд электрона e=-|e|<0.
Ввиду сферической симметрии

его СЗ E_nl⁰ вырождены с кратностью

, равной числу возможных значений проекции момента на ось z. Включение магнитного поля нарушает сферическую симметрию системы и приводит к снятию вырождения по квантовому числу m: уровни энергии E_nl⁰ расщепляются на

подуровней.
Замечание. Для чисто кулоновского потенциала в атоме водорода

имеется (случайное) вырождение уровней энергии по

, которое объясняется дополнительной, кроме сферической, симметрией этого потенциала (см. ниже п. 10).
Итак, теория Шредингера предсказывает, что в магнитном поле уровни энергии атома должны расщепляться на нечетное число подуровней, образующих мультиплет. Эксперимент частично подтверждает это предсказание (эффект Зеемана: P. Zeeman, 1896). Расщепление имеет более сложную структуру: оно зависит от типа атома и различно для разных мультиплетов одного и того же атома. В частности, наблюдаются как нечетные, так и четные мультиплеты, как если бы

было полуцелым.
Более того, обнаруживается тонкая структура уровней даже в отсутствие внешнего магнитного поля. Рассмотрим, например, уровень валентного электрона в щелочном атоме натрия, отвечающий

(так называемый 2p-терм). По теории Шредингера имеем вырождение уровня энергии кратности 3. Эксперимент же показывает, что этот уровень расщеплен на два близких подуровня ( при B=0!).
Особенно наглядно противоречие теории и эксперимента проявилось в опытах Штерна и Герлаха (O. Stern, W. Gerlach, 1922). Они пропускали узкий пучок атомов водорода, находящихся в основном состоянии

, через область неоднородного магнитного поля и обнаружили, что пучок расщепляется на два пучка. Результаты опытов можно объяснить, предполагая, что атом водорода в основном состоянии обладает некоторым магнитным моментом. Тогда гамильтониан нейтрального атома, рассматриваемого как единая частица с нулевым электрическим зарядом и взаимодействующего с магнитным полем, записывается в виде (ср. выше):

$hat H=frac{{bfhat p}^2}{2m_H}-{bf Mcdot B},$

где B=B(r) - макроскопически неоднородное магнитное поле. На основе этого гамильтониана можно показать, что если z-компонента поля B_z значительно больше компонент B_x и B_y, то на атом, влетающий в область поля перпендикулярно оси z, начинает действовать средняя сила

${bf F}=M_zfrac{partial B_z}{partial z}{bf e_z}.$

Эксперимент показал, что проекция магнитного момента атома в основном состоянии на заданное направление может принимать только два значения:

где

- введенный выше магнетон Бора. Учтем, что в основном состоянии орбитальный момент электрона равен нулю, а масса ядра атома водорода (протона) значительно больше массы электрона. Тогда естественно предположить, что электрон обладает собственным магнитным моментом

, величина которого равна

(по определению это максимальное значение проекции

). При этом магнитный момент электрона пропорционален его собственному моменту импульса (спину) S:

${bfmu}=g_S {bf S},$

где коэффициент пропорциональности g_S - спиновое гиромагнитное отношение. Результаты эксперимента можно интерпретировать так:

$M_z=mu_z=pm mu_B=g_S S_z,; S_z=mpfrac{hbar}{2},; g_S=frac{e}{m_e c}=2g_L,$

где учтено, что g_S<0 (e<0).
Заметим, что гипотезу о существовании спина электрона выдвинули Уленбек и Гаудсмит (G. Uhlenbeck, S. Goudsmit, 1925), предложившие модель электрона в виде заряженного шарика, вращающегося вокруг своей оси. Хотя это полуклассическая модель объясняет пропорциональность магнитного и механического моментов (см. выше выражение для магнитного момента вращающегося шарика), но дает неправильное значение спинового гиромагнитного отношения, равное орбитальному, а из эксперимента следует в два раза большее значение. Кроме того, эта модель противоречит теории относительности. Действительно, приравняем магнитный момент шарика магнетону Бора и найдем скорость точки на экваторе:

$frac{ea^2}{5c}omega=frac{ehbar}{2m_e c},; v=omega a=frac{5}{2}cfrac{lambda_e}{a},$

где $lambda_e=hbar/m_e c=3,!86cdot 10^{-11} cм$ - комптоновская длина волны электрона (см. п. 1). Следовательно, при

имеем v>2,5c, т.е. больше скорости света в вакууме (!).
Подчеркнем, что в квантовой механике электрон рассматривается как точечная (бесструктурная) частица. Это подтверждается экспериментом и показывает, в частности, что спин не имеет классического аналога.

Уравнение Паули

Спин в аппарат квантовой механики был введен Паули. Он предложил (постулировал) для описания электрона уравнение, которое теперь называется уравнением Паули (W. Pauli, 1927):

$ihbar frac{partialpsi}{partial t}=hat H_ppsi,; hat H_p=frac{1}{2m_e}left({bfhat p}-frac{e}{c}{bf A}right)^2+ePhi-{bfhatmucdot B}.$

Паулиевский гамильтониан

отличается от шредингеровского добавлением слагаемого $hat U_p=-{bfhatmucdot B}$ , описывающего взаимодействие с магнитным полем

спинового магнитного момента электрона, представляемого оператором

${bfhatmu}=g_S {bfhat S}=-mu_B{bfsigma}.$

Этот оператор введен по аналогии с оператором орбитального магнитного момента ${bfhat M}=g_L{bfhat L}$ .
Как уже обсуждалось выше, волновая функция электрона

в теории Паули является двухкомпонентной:

$psi=left(begin{array}{l} psi_1 psi_2end{array}right).$

Она называется спинором и преобразуется при поворотах системы координат по двузначному представлению группы вращений (см. выше). В частности, при повороте на

получим преобразование

$psitopsi'=-psi=e^{ipi}psi.$

Следовательно, для спинора этот поворот не эквивалентен тождественному преобразованию, как это имеет место для скаляра и вектора.
Рассмотрим "вывод" уравнения Паули, принадлежащий Фейнману (R.P. Feynman). Из основного соотношения для матриц Паули (см. выше),

$sigma_ksigma_n=delta_{kn}+ivarepsilon_{kns}sigma_s,$

следует тождество

где a,b - произвольные векторы. Учитывая его, запишем гамильтониан электрона в электрическом поле в эквивалентном шредингеровскому виде

$hat H=frac{({bfsigmacdothat p})^2}{2m_e}+ePhi.$

Введем теперь взаимодействие с магнитным полем по известному правилу (это, конечно, постулат):

${bfhat ptohat P=hat p}-frac{e}{c}{bf A}.$

Тогда получим гамильтониан

$hat H_F=frac{({bfsigmacdothat P})^2}{2m_e}+ePhi$

который эквивалентен гамильтониану Паули:

Действительно, имеем

$({bfsigmacdothat P})^2={bfhat P}^2+i{bfsigmacdot(hat Ptimeshat P)},$

где второе слагаемое отлично от нуля ввиду некоммутативности компонент оператора кинетического импульса

$[hat P_n,hat P_k]=[hat p_n-frac{e}{c}A_n,hat p_k-frac{e}{c}A_k]=ihbarfrac{e}{c}(partial_n A_k-partial_k A_n).$

Следовательно,

$({bfhat Ptimeshat P})_s=varepsilon_{snk}hat P_nhat P_k=frac{1}{2}varepsilon_{snk}[hat P_n,hat P_k]=ihbarfrac{e}{c}varepsilon_{snk}partial_n A_k,$

или

${bfhat Ptimeshat P}=ihbarfrac{e}{c}{bf B},; {bf B=nablatimes A}.$

В результате получаем:

$frac{({bfsigmacdothat P})^2}{2m_e}=frac{{bfhat P}^2}{2m_e}-frac{ehbar}{2m_e c}{bfsigmacdot B},$

т.е. приходим к паулиевскому взаимодействию спинового магнитного момента электрона с магнитным полем.

Движение в центрально-симметричном поле

Рассмотрим движение частицы в стационарном поле $U=U(r),; r=|{bf r}|=sqrt{{x^2+y^2+z^2}}$ . Такое поле называется центрально-симметричным, или, коротко, центральным. В этом случае гамильтониан

$hat H=frac{{bf p}^2}{2m_e}+U(r)$

коммутирует с оператором орбитального момента:

Покажем это подробнее, получив следующее представление оператора квадрата импульса:

${bf hat p}^2=-hbar^2nabla^2=-frac{hbar^2}{r^2}frac{partial}{partial r}left(r^2frac{partial}{partial r}right)+frac{{bfhat L}^2}{r^2}.$

Имеем:

${bf hat L^2=(rtimeshat p)^2=-(hat ptimes r)cdot(rtimeshat p)=-hat pcdot(rtimes(rtimeshat p))=-hat pcdot(r(rcdothat p)}-r^2{bfhat p}).$

Из фундаментального соотношения $[hat p_n,x_m]=-ihbardelta_{nm}$ следуют коммутаторы

$[{bf hat pcdot r, rcdot hat p}]=-3ihbar,; [{bfhat p},r^2]=-2ihbar{bf r},$

используя которые, находим

${bfhat L}^2=r^2{bf hat p}^2-({bf rcdot hat p})^2+ihbar{bf rcdothat p}.$

Далеe:

${bf rcdothat p}=-ihbar{bf rcdotnabla}=-ihbar rfrac{partial}{partial r},; ({bf rcdothat p})^2=-hbar^2left(rfrac{partial}{partial r}+r^2frac{partial^2}{partial r^2}right).$

В итоге получаем приведенное выше выражение для ${bf hat p}^2$ , откуда сразу видно, что $[{bf hat L,hat p^2}]=0$ .
Стационарное уравнение Шредингера

для частицы в центральном поле принимает вид:

$left[-frac{hbar^2}{2m_e r^2}frac{partial}{partial r}left(r^2frac{partial}{partial r}right)+frac{{bfhat L^2}}{2m_er^2}+U(r)right]psi=Epsi.$

Так как момент

- интеграл движения, то любая собственная функция гамильтониана представляется в виде произведения радиальной функции, зависящей только от r, и сферической функции (см. п. 7):

т.е. является собственной функцией полного набора наблюдаемых (спин мы не учитываем) $hat H,{bf hat L^2}, hat L_z$ .
Для радиальной функции получаем уравнение

$left[-frac{hbar^2}{2m_e r^2}frac{d}{dr}left(r^2frac{d}{dr}right)+frac{hbar^2ell(ell+1)}{2m_e r^2}+U(r)right]R=ER.$

Удобно ввести новую функцию согласно

$R(r)=frac{chi(r)}{r}.$

Она удовлетворяет радиальному уравнению Шредингера:

$left[-frac{hbar^2}{2m_e}frac{d^2}{dr^2}+U_ell(r)right]chi=Echi,$

где введен эффективный потенциал

$U_ell(r)=U(r)+frac{hbar^2ell(ell+1)}{2m_er^2}.$

Мы получили уравнение Шредингера для движения частицы на полупрямой

в потенциальном поле

.
Замечание. Даже для свободной частицы (U=0) в состоянии с заданным моментом эффективный потенциал отличен от нуля при

и совпадает с центробежным потенциалом

.
Условие нормировки для

совпадает с условием нормировки одномерной волновой функции в силу ортонормированности сферических функций:

$int d^3 x|psi|^2=intlimits_{0}^{infty}drr^2|R|^2=intlimits_{0}^{infty}dr|chi|^2=1.$

Для физических приложений интерес представляют потенциалы, для которых выполняется условие

т.е. не более сингулярные, чем $1/r^{2-varepsilon},; varepsilon gt 0$ , . Спектр радиального гамильтониана

$hat H_ell=-frac{hbar^2}{2m_e}frac{d^2}{dr^2}+U(r)+frac{hbar^2ell(ell+1)}{2m_e r^2}$

хорошо изучен для широкого класса потенциалов U(r).
Выясним асимптотику радиальной функции

при

. Оставляя наиболее сингулярный член в радиальном УШ, получаем:

$chi''-ell(ell+1)r^{-2}chi=0.$

Ищем решение в виде

Получаем для степени s уравнение

откуда

, т.е.

$chisim r^{-ell}$ или $chisim r^{ell+1}.$

Учитывая, что полная волновая функция имеет вид

$psi=frac{chi(r)}{r}Y_l^m(theta,varphi),$

из требования непрерывности

получаем граничное условие

Следовательно, правильное асимптотическое поведение

таково:

$chi(r)cong Cr^{ell+1}$ при $rto 0.$

Атом водорода

Электрон в поле кулоновского центра

Задача об атоме водорода - одна из фундаментальных проблем квантовой механики, успешное решение которой способствовало дальнейшему развитию теории.
Атом водорода состоит из тяжелого ядра (протона массы

) и движущегося в его кулоновском поле электрона. Сначала будем считать ядро бесконечно тяжелым, заменив его неподвижным кулоновским центром (конечность массы ядра учтем позже). Тогда гамильтониан атома можно записать в виде гамильтониана электрона в центральном поле:

$hat H = -frac{hbar^2}{2m_e}nabla^2-frac{alpha}{r}$

, где

. Здесь Z - заряд ядра в единицах заряда электрона, причем Z=1 отвечает атому водорода H, а Z=2,3,... - водородоподобным ионам He⁺, Li⁺⁺,...
Используя результаты п. 9, запишем волновую функцию стационарного состояния электрона, которая является собственной для полного набора наблюдаемых

$psi (r) = frac{chi (r)}{r}Y_ell^m(theta,varphi$

. Для радиальной функции

получаем уравнение

$frac{d^2chi}{dr^2} + frac{2m}{hbar^2}left(E+frac{alpha}{r}-frac{hbar^2ell(ell + 1)}{2m_er^2}right)chi =0$

. Нетрудно показать, что при E>0 спектр гамильтониана непрерывен. В этом случае

, но

, что отвечает инфинитному движению электрона, и атом водорода как связанная система электрона и ядра не существует. Мы ограничимся поэтому рассмотрением дискретного спектра: E<0.
Обозначим

$k^2 = -frac{2m_eE}{hbar^2} gt 0$

и введем вместо r безразмерную переменную

. Тогда уравнение на собственные значения примет вид:

$frac{d^2chi}{drho^2}+left[-1+frac{lambda}{rho}-frac{ell (ell +1)}{rho^2}right]chi =0$

, введен параметр

$lambda = frac{2m_ealpha}{hbar^2 k}=left[-frac{2m_ealpha^2}{hbar^2E}right]^{1/2}$

. Рассмотрим асимптотику ограниченного решения

. При

имеем (см. п. 9)

$chicongchi_0=C_0rho^{ell+1}$

. При

получаем приближенное уравнение

, откуда

$chicongchi_infty=C_infty e^{-rho}$

. Поэтому ищем решение в виде

$chi=rho^{ell+1}e^{-rho}v(rho)$

. Подставляя его в уравнение на СЗ, находим для функции v уравнение:

$v'' +2left(frac{ell+1}{rho}-1right)v'+frac{1}{rho}[lambda -2(ell +1)]v=0$

. Решение ищем в виде ряда:

$v=sumlimits_{k=0}^{infty}a_krho^k$

, причем

, чтобы обеспечить правильную асимптотику

при

. Подставив ряд в уравнение, после очевидных замен индекса суммирования k получим:

$sumlimits_{k=0}^{infty}rho^{k-1}left{a_{k+1}[k(k+1)+2(ell +1)(k+1)]-a_k[2(k+ell +1)-lambda ]right}=0$

. Отсюда следует рекуррентное соотношение для коэффициентов ряда:

$a_{k+1}=frac{2(k+ell +1)-lambda}{(k+1)[k+2(ell +1)]}a_k$

. Ряд сходится при всех

по признаку Даламбера:

$limlimits_{ktoinfty}^{}frac{a_{k+1}}{a_k}=0$

. Его асимптотическое поведение при больших

определяется коэффициентами a_k при

$a_{k+1}congfrac{2}{k+1}a_kto a_kcong Cfrac{2^k}{k!}$

, откуда

$vcong Ce^{2rho}$

, т.е. для произвольного положительного параметра

имеем при

неприемлемую асимптотику радиальной функции:

$chicong Crho^{ell +1}e^rho$

. Однако существуют такие дискретные значения

, при которых функция

становится полиномом:

. Тогда $a_{n_r} ne 0, a_k=0$ при $kge n_r+1$ . Вспомнив определение

$lambda^2 =-frac{2m_ealpha^2}{hbar^2 E}$

, приходим к дискретному спектру атома водорода и водородоподобных ионов:

$E_n=-frac{m_ealpha^2}{2hbar^2}cdotfrac{1}{n^2}, n=1,2,ldots$

. Здесь введено главное квантовое число n, связанное с радиальным n_r и орбитальным

квантовыми числами соотношением

. При заданном n орбитальное число

может принимать n значений:

. Соответствующие волновые функции стационарных состояний имеют вид:

$psi_{nell m}(r)=rho^ell e^{-rho}v_{nell}(rho)Y_ell^m (theta,varphi)$

, где

$rho =k_n r, k_n =left[-frac{2m_e}{hbar^2}E_nright]^{1/2}=frac{m_ealpha}{hbar^2}cdotfrac{1}{n}$

. Полином $v_{nell}(rho)$ имеет степень

, равную числу его нулей (узлов). Коэффициенты a_k при k>0 выражаются через a₀ с помощью полученной выше рекуррентной формулы, а a₀ определяется из условия нормировки:

$k_n^{-3}intlimits_{0}^{infty}drhorho^{2+2ell}e^{-2rho}v_{nell}(rho)=1$

.
Замечание. Можно показать, что $v_{nell}$ выражаются через обобщенные полиномы Лагерра

$Q_k^s (x)=e^x x^{-s}frac{d^k}{dx^k}left(e^{-x}x^{k+s}right)$

, и нормированная волновая функция имеет вид:

$psi_{nell m}(r)=2[n(n-ell -1)!(n+ell)!]^{-1/2}k_n^{3/2}(2rho)^ell e^{-rho}Q_{n-ell -1}^{2ell +1}(2rho)$

.
Мы видим, что собственные значения энергии вырождены с кратностью

$sumlimits_{ell=0}^{n-1}sumlimits_{m=-ell}^{ell}(2ell+1)=n^2$

.
Учет спина (две возможные проекции спинового момента на заданное направление) дает кратность d_n=2n², но спектр атома водорода в теории Паули не изменяется, так как отсутствует взаимодействие спинового магнитного момента с магнитным полем. Учет релятивистских эффектов (порядка $(v/c)^2sim(e^2/hbar c)^2approx 5cdot 10^{-5}$ в атоме водорода) приводит к появлению тонкой структуры спектра. В частности, возникает спин-орбитальное взаимодействие

, т.е. взаимодействие спинового магнитного момента с внутриатомным магнитным полем, источником которого является орбитальное движение электрона.
Рассмотрим подробнее атом водорода (Z=1). Мы имеем атомную единицу длины

$a_B = frac{1}{k_1}=frac{hbar^2}{m_e e^2} =0,529cdot 10^{-8} см$

- боровский радиус (в полуклассической теории это радиус первой боровской орбиты: см. п. 1) и атомную единицу энергии - ридберг:

$Ry=hbar R=frac{m_e e^4}{2hbar^2}=2,18cdot 10^{-11} эрг = 13,6 эВ$

, где R - постоянная Ридберга, входящая в выражение для спектральных частот излучения.
Энергия основного состояния атома водорода (главное квантовое число n=1) равна

E₁ =-Ry = -13,6 эВ

. Величина I=|E₁| называется потенциалом ионизации. Он равен энергии связи электрона в атоме, определяемой как работа, которую нужно совершить, чтобы удалить электрон из атома.
Квантовая электродинамика (теория, объединяющая квантовую механику электрона и квантовую теорию электромагнитного поля на основе теории относительности) подтверждает гипотезу Бора о частотах спектральных линий:

$hbaromega_{n'n}=E_n -E_{n'}, E_n gt E_{n'}$

. Используя полученное выражение для E_n, приходим к известной формуле Бальмера (п.1):

$omega_{n'n}=frac{Ry}{hbar}left(frac{1}{n'^2}-frac{1}{n^2}right),n' lt n$

. Фиксируя n' и меняя n, получим различные спектральные серии. Укажем некоторые из них: n'=1 - серия Лаймана (ультрафиолетовая часть спектра излучения); n'=2 - серия Бальмера (первые 4 линии попадают в видимую часть спектра); n'=3 - серия Пашена (инфракрасная часть спектра).
Важные характеристики атома - вероятности переходов между стационарными состояниями w_n'n. Они определяют интенсивности соответствующих спектральных линий, т.е. мощность излучения W_n'n на частоте $omega_{n'n}$ . Заметим, что величина $tau_{n'n}=1/w_{n'n}$ имеет смысл среднего времени жизни электрона на уровне E_n относительно перехода

, или временного интервала, в течение которого испускается фотон с энергией $hbaromega_{n'n}$ . Поэтому

$W_{n'n}=omega_{n'n}w_{n'n}$

. Согласно квантовой электродинамике в главном (дипольном) приближении (малым параметром является отношение размера атома к длине волны испускаемого фотона) вероятность перехода выражается через матричные элементы r_n'n оператора координаты электрона:

$w_{n'n}=frac{4omega_{n'n}^3}{3hbar c^3}|r_{n'n}|^2$

. Здесь матричный элемент представляет собой интеграл, содержащий квадратичные комбинации волновых функций:

$r_{n'n}=(psi_{n'},rpsi_n)=int d^3 xpsi_{n'}^* rpsi_n$

. Для атома водорода индекс состояния n обозначает набор трех квантовых чисел (см. выше):

. Для некоторых переходов матричный элемент, а вместе с ним и интенсивность соответствующей спектральной линии, могут обращаться в нуль. Условия, при которых $r_{n'n}ne 0$ , называются правилами отбора. Можно показать, что для атома водорода (и водородоподобных атомов) они имеют вид:

, причем

произвольно (1,2,...). Правила отбора выражают закон сохранения момента импульса при испускании фотона (спин его равен

) электроном.
Рассмотрим основное состояние атома водорода:

. Угловая часть волновой функции $Y_0^0 =1/sqrt{4pi}$ . Для радиальной части $R_{10}=e^{-rho}v_{10}$ имеем

, т.е. v₁₀ - полином нулевой степени. Учитывая связь

получаем полную функцию:

$psi_{100}(r)=Ce^{-r/a_B}$

. Нормируем ее:

$|C|^2int dOmegaintlimits_{0}^{infty}drr^2e^{-2r/a_B}=4pi |C|^2(a_B/2)^3intlimits_{0}^{infty}dxx^2e^{-x}=1$

. Итак, нормированная волновая функция основного состояния имеет вид:

$psi_{100}(r)=(pi a_B^3)^{-1/2}e^{-r/a_B}$

.
Плотность вероятности обнаружить электрон на расстоянии r от ядра равна

$w(r)=int dOmega r^2|psi |^2=4a_B^{-3}r^2e^{-2r/a_B}$

. Максимум вероятности достигается на расстоянии r=r_m, определяемом из условия

$frac{dw}{dr}=0$

. Получаем в результате r_m=a_B. Следовательно, радиус первой боровской орбиты - расстояние от ядра, на котором вероятность обнаружить электрон максимальна. Поскольку при

плотность экспоненциально мала, то можно сказать, что эффективный размер атома водорода порядка a_B~ 10^-8 см.
Мы видим, что в основном состоянии распределение по координатам сферически симметрично. Это не так в возбужденных состояниях при

.
Замечание. Угловое распределение вероятности универсально, т.е. одинаково для всех сферически-симметричных потенциалов (см. явный вид некоторых сферических функций

в п. 7). Что же касается вырождения уровней энергии по орбитальному числу

, то оно характерно только для двух типов потенциалов U(r): кулоновского (U~1/r) и потенциала трехмерного осциллятора (U~r²). В.А. Фок (1935) показал, что "случайное" вырождение по

в кулоновском поле объясняется наличием более широкой, чем SO(3), группы симметрии SO(4). Это приводит к дополнительному интегралу движения

$hat A=frac{{bf r}}{r}+frac{1}{2malpha}left(hat Ltimeshat p-hat ptimeshat Lright)$

, причем

. Наблюдаемая

- аналог известного в классической механике вектора Рунге-Ленца, или вектора эксцентриситета: он направлен от фокуса эллиптической орбиты по большой оси к наиболее удаленной точке траектории, а его модуль равен эксцентриситету эллипса.

Учет движения ядра

Учтем теперь конечность массы ядра атома. Тогда получаем гамильтониан системы двух частиц - электрона и ядра:

$hat H=frac{hat p_1^2}{2m_e}+frac{hat p_2^2}{2M}+U(|r_1-r_2|)$

. Введем новые координаты - относительные и центра масс:

$r=r_1-r_2, R=frac{m_e r_1 + Mr_2}{m_e + M}$

. Соответствующие операторы импульсов имеют вид:

. С учетом соотношения

$frac{partial}{partial x_k}=frac{partial r}{partial x_k}cdotnabla_r + frac{partial R}{partial x_k}cdotnabla_R$

получим гамильтониан в новых переменных:

$hat H=frac{hat p^2}{2mu}+frac{hat P^2}{2M_0}+U(r)$

. Здесь

$mu=frac{m_e M}{m_e+M}cong m_eleft(1-frac{m_e}{M}right)$

- приведенная масса,

- полная масса атома.
В силу

собственная функция гамильтониана

представляется в виде функции, отвечающей движению центра масс с заданным импульсом P, и волновой функции относительного движения

$Psi (r,R)={rm exp}left(frac{i}{hbar}Pcdot Rright)psi (r)$

. В системе центра масс (P=0) для

получаем уравнение

$left[frac{hat p^2}{2mu}+U(r)right]psi (r)=Epsi (r)$

. В результате мы пришли к уже исследованной задаче: движение частицы массы

в центральном поле U(r) (в нашем случае - неподвижного кулоновского центра

). Таким образом, как и в классической механике, задача двух тел сводится к задаче одного тела.
Спектр энергии определяется известной формулой с заменой там массы электрона m_e на приведенную массу

, т.е. следующей заменой постоянной Ридберга, отвечающей бесконечной массе ядра:

$Requiv R_infty=frac{m_e e^4}{2hbar^3}to R_M=frac{mu e^4}{2hbar^3}cong R_inftyleft(1-frac{m_e}{M}right).$

Уточненный спектр излучения водородоподобного атома принимает вид:

$omega_{n'n}=Z^2 R_inftyleft(1-frac{m_e}{M}right)left(frac{1}{n'^2}-frac{1}{n^2}right).$

Учет движения ядра позволил объяснить некоторые эффекты. Рассмотрим серии Бальмера (n'=2) обычного водорода H=¹₁H=(p) и его изотопов дейтерия D=²₁H=(pn) и трития T=³₁H=(pnn), где в скобках указан протон-нейтронный состав ядер:

$omega^{(i)}_{2n}=R_infty(1-delta_i)left(frac{1}{2^2}-frac{1}{n^2}right),; H,D,T;; delta_H=frac{1}{1840},; delta_D=frac{1}{3680},; delta_T=frac{1}{5520}.$

Мы видим, что поправки к спектру на конечность массы ядра

различны для разных изотопов. Следовательно, изотопы могут быть обнаружены спектроскопическими методами, так как их соответствующие спектральные линии немного сдвинуты относительно друг друга. Это и было сделано фактически. Оказалось, что в естественной смеси изотопов, природной воде, относительная концентрация изотопов водорода такова: $D/Happrox 1/6800,; T/Happrox 10^{-18}.$
Другое важное приложение теории - объяснение обнаруженной в спектре излучения Солнца спектральной серии Пикеринга. Она приближенно описывается формулой, похожей на формулу Бальмера для атома водорода:

$omega^{(H)}_{2n_1}=R_Hleft(frac{1}{2^2}-frac{1}{n_1^2}right),$

но содержит "лишние" линии, так как квантовое число n₁ принимает не только целые, но и полуцелые значения:

n₁=5/2,3,7/2,4,9/2,...,

которые запрещены для водорода. Правильная интерпретация этой серии была дана, когда более точные спектроскопические измерения показали, что линии несколько сдвинуты по сравнению с водородными линиями так, что в указанной формуле следует сделать замену

$R_H=R_inftyleft(1-frac{1}{1840}right)to R_{He}=R_inftyleft(1-frac{1}{7360}right).$

Полагая там же n₁=n/2, получим формулу, не содержащую полуцелых квантовых чисел:

$omega^{(He)}_{4n}=2^2 R_{He}left(frac{1}{4^2}-frac{1}{n^2}right),; n=5,6,7,ldots.$

Она описывает спектральную серию однократно ионизованного атома гелия ⁴₂He⁺=(ppnn), т.е. водородоподобного иона с Z=2.

Тождественные частицы. принцип паули

Системы многих частиц

Пространство состояний одной бесспиновой частицы H=L²(R³), частицы со спином 1/2 (в единицах

) - H=L²(R³)

C². Для системы частиц имеем соответственно

${bf H}=L^2({bf R}^{3N})=L^2({bf R}^3)otimescdotsotimes L^2({bf R}^3)$

${bf H}=L^2({bf R}^{3N})otimes C^{2N}=(L^2({bf R}^3)otimes C^2)otimescdotsotimes (L^2({bf R}^3)otimes C^2).$

Эксперимент показывает, что эта структура пространства состояний справедлива только для систем различных частиц. Волновая функция системы

где

$xi_n=({bf r_n},zeta_n)$

- набор пространственных координат r_n и дискретной спиновой переменной

n-ой частицы. Скалярное произведение в этом пространстве

$(psi,varphi)=int dxi_1cdots dxi_Npsi^*(xi)varphi(xi),; int dxi_nequivint d^3 x_nsumlimits_{xi_n}^{}.$

В квантовой механике одинаковые частицы принципиально неразличимы. Постулаты теории, сформулированные в п. 4, дополняются новым - принципом тождественности (неразличимости одинаковых частиц).
Принцип тождественности: пространством состояний системы N одинаковых (тождественных) частиц является пространство H_S симметричных функций или пространство H_A антисимметричных функций.
Определим соответствующие функции

. Для этого рассмотрим группу перестановок N элементов P_N. Ее элементы - перестановки

$P=left( begin{array}{ccc} 1, & 2,ldots, & N k_1, & k_2,ldots, & k_N end{array} right), ; k_i=overline{1,N};; k_ine k_j,$

причем единичный элемент - тождественная перестановка

а произведение перестановок P₂P₁ - результат двух последовательных перестановок P₁ и P₂. В пространстве волновых функций H перестановке P отвечает оператор

, действующий так:

$hat Ppsi(xi_1,xi_2,ldots,xi_N)=psi(xi_{k_1},xi_{k_2},ldots,xi_{k_N}).$

Очевидно, что

- унитарный оператор и отображение

есть представление группы P_N в пространстве H. В H выделяются два инвариантных относительно операторов

подпространства симметричных и антисимметричных функций:

${bf H_S}=(psi_S),; {bf H_A}=(psi_A).$

Эти функции - собственные функции операторов перестановки:

Здесь введена четность перестановки $delta_P=(-1)^{n_P}=+1(-1)$ для четного (нечетного) числа n_P последовательных перестановок двух частиц, к которым сводится данная перестановка P.
Очевидно, что ${bf H_Aperp H_S}$ . В случае N=2 имеем

${bf H=H_Aoplus H_S}.$

Действительно,

$psi(xi_1,xi_2)=frac{1}{2}[psi(xi_1,xi_2)+psi(xi_2,xi_1)]+frac{1}{2}[psi(xi_1,xi_2)-psi(xi_2,xi_1)]=psi_S+psi_A.$

При

имеются и другие, более сложные, чем H_A и H_S, инвариантные подпространства, но они не имеют физических приложений.
Частицы, описываемые функциями

, называются бозонами (фермионами) и подчиняются статистике Бозе - Эйнштейна (Ферми - Дирака).
В квантовой механике постулируется следующая связь спина и статистики: частицы с целым спином (s=0,1,2,...) являются бозонами, частицы с полуцелым спином (s=1/2,3/2,5/2,...) - фермионами.
Замечание. В квантовой теории поля указанная связь спина и статистики представляет собой теорему, доказанную В. Паули (W. Pauli, 1940) на основе принципа причинности и лоренц-инвариантности.
Статистика составных тождественных частиц (например, атомных ядер) определяется четностью числа входящих в их состав фермионов. Например, дейтрон ( ядро атома дейтерия D=²₁H=(pn)), состоящее из двух частиц со спином 1/2, протона и нейтрона, является бозоном.
Гамильтониан системы N тождественных попарно взаимодействующих частиц массы m во внешнем поле V(r) имеет вид:

$hat H=-sumlimits_{n=1}^{N}frac{hbar^2}{2m}nabla^2_n+sumlimits_{n=1}^{N}V({bf r_n}) +sumlimits_{n lt n'} U({bf r_n - r_n'})$

где U - потенциал парного взаимодействия. В силу одинаковости масс частиц и независимости потенциалов V и U от номеров частиц оператор перестановки

- интеграл движения:

Следовательно, в процессе эволюции системы согласно уравнению Шредингера

$ihbarfrac{partialpsi}{partial t}=hat Hpsi$

тип симметрии волновой функции не изменяется. Иначе говоря, связь спина и статистики не разрушается динамикой, как и должно быть в непротиворечивой теории.
Рассмотрим важный частный случай системы невзаимодействующих частиц (U=0) во внешнем поле. Гамильтониан такой системы представляется в виде суммы гамильтонианов отдельных частиц:

$hat H=sumlimits_{n=1}^{N}hat H_n,; hat H_n=-frac{hbar^2}{2m}nabla_n^2+V({bf r_n}).$

Решение стационарного уравнения Шредингера,

, можно искать в виде произведения одночастичных волновых функций:

$psi_П (xi_1,ldots,xi_N)=prodlimits_{n=1}^{N}psi_n(xi_n),; (hat H_n-varepsilon_n)psi_n=0,; E=sumlimits_{n=1}^{N}varepsilon_n.$

Функция

не удовлетворяет принципу тождественности, хотя и является решением УШ. Поскольку оператор перестановки - интеграл движения, то функция

- также решение УШ:

Поэтому правильные решения определенной симметрии

получаются путем составления (анти)симметричных линейных комбинаций функций

Принцип Паули

Для системы фермионов получаем антисимметричную функцию, которую можно записать в виде определителя Слэтера (J. Slater, 1929):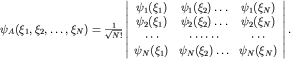

$psi_A(xi_1,xi_2,ldots,xi_N)=frac{1}{sqrt{N!}}left| begin{array}{ccc} psi_1(xi_1) & psi_1(xi_2)ldots & psi_1(xi_N) psi_2(xi_1) & psi_2(xi_2)ldots & psi_2(xi_N) cdots & cdots cdots & cdots psi_N(xi_1) & psi_N(xi_2)ldots & psi_N(xi_N) end{array} right|.$

Здесь нормировочный коэффициент включает N! - число перестановок среди частиц N.
Интерпретация функций

такова.
Функция

("неправильная") описывает состояние системы, в котором 1-я частица находится в одночастичном состоянии

, 2-я частица - в состоянии

и т. д.
Правильная функция

отвечает состоянию, в котором N частиц заполняют N одночастичных состояний, причем нельзя указать, какая частица в каком именно состоянии находится, что согласуется с принципиальной неразличимостью тождественных частиц (им невозможно приписать номера). Если среди одночастичных функций

есть одинаковые, то

в силу известного свойства определителя, содержащего одинаковые строки. Это означает неосуществимость такого состояния и приводит к принципу Паули (W. Pauli, 1924-25), сформулированном им первоначально для электронов: в одном и том же одночастичном состоянии не может находиться более одного фермиона.
Подчеркнем, что принцип Паули - следствие антисимметричности волновой функции, и поэтому он справедлив только для фермионов.

Система двух электронов

Волновая функция двухэлектронной системы удовлетворяет условию антисимметрии:

Определим сначала оператор спина системы:

${bf hat S=hat S^{(1)}+hat S^{(2)}},; {bf hat S^{(n)}}=frac{hbar}{2}{bf sigma^{(n)}}.$

Здесь индексы (1) и (2) нумеруют спиновые подпространства отдельных электронов в спиновом пространстве системы

. В каждом из подпространств C² имеем базисные векторы:

$u^{(n)}=left(begin{array}{c} 1 0 end{array}right)^{(n)},; d^{(n)}=left(begin{array}{c} 0 1 end{array}right)^{(n)},$

которые являются собственными векторами операторов ${bfhat S^{(n)^2}}$ и $S_z^{(n)}$ . В пространстве C⁴ в качестве базиса можно выбрать 4 вектора

u⁽¹⁾u⁽²⁾, d⁽¹⁾d⁽²⁾, u⁽¹⁾d⁽²⁾, d⁽¹⁾u⁽²⁾.

Удобно выбрать новый базис, состоящий из собственных векторов операторов квадрата полного спина и его проекции на ось z:

${bfhat S}^2=frac{hbar^2}{4}({bfsigma^{(1)} + sigma^{(2)}})^2=frac{hbar^2}{2}(3I+{bfsigma^{(1)}cdotsigma^{(2)}}),; hat S_z=frac{hbar}{2}(sigma^{(1)}_3+sigma^{(2)}_3).$

Замечание. Мы используем здесь сокращенную запись операторов двухчастичной системы. Точная запись, например, оператора проекции спина такова:

$hat S_z=frac{hbar}{2}(sigma_3otimes I+Iotimessigma_3).$

Легко проверить, что указанный базис имеет вид:

$chi_{1,-1}=d^{(1)}d^{(2)},; chi_{1,0}=frac{1}{sqrt{2}}(u^{(1)}d^{(2)}+d^{(1)}u^{(2)},; chi_{1,1}=u^{(1)}u^{(2)},; chi_{0,0}=frac{1}{sqrt{2}}(u^{(1)}d^{(2)}-d^{(1)}u^{(2)}.$

Смысл индексов векторов $chi_{S,zeta}$ таков:

${bfhat S}^2chi_{S,zeta}=hbar^2 S(S+1)chi_{S,zeta},; hat S_zchi_{S,zeta}=hbarzetachi_{S,zeta}.$

Прямая проверка проводится с помощью формул:

Например,

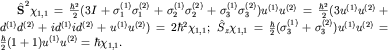${bfhat S}^2chi_{1,1}=frac{hbar^2}{2}(3I+sigma_1^{(1)}sigma_1^{(2)}+ sigma_2^{(1)}sigma_2^{(2)}+sigma_3^{(1)}sigma_3^{(2)})u^{(1)}u^{(2)}=frac{hbar^2}{2}(3u^{(1)}u^{(2)}+d^{(1)}d^{(2)}+id^{(1)}id^{(2)}+u^{(1)}u^{(2)})=2hbar^2chi_{1,1}; ; hat S_zchi_{1,1}=frac{hbar}{2}(sigma_3^{(1)}+sigma_3^{(2)})u^{(1)}u^{(2)}=frac{hbar}{2}(1+1)u^{(1)}u^{(2)}=hbarchi_{1,1}.$

Следовательно,

.
С точки зрения теории групп мы доказали, что

$D_{1/2}otimes D_{1/2}=D_0oplus D_1.$

Это частный случай теоремы о разложении прямого (тензорного) произведения неприводимых представлений D_j группы SO(3) в прямую сумму неприводимых представлений:

$D_{j_1}otimes D_{j_2}=D_{|j_1-j_2|}oplus D_{|j_1-j_2|+1}opluscdotsoplus D_{j_1+j_2}=bigopluslimits_{J=|j_1-j_2|}^{j_1+j_2}D_J.$

Базисные векторы в пространстве представления D_J размерности 2J+1 имеют вид:

$e_{j_1j_2JM}=sumlimits_{m_1=-j_1}^{j_1}sumlimits_{m_2=-j_2}^{j_2}C(j_1j_2JM|j_1j_2m_1m_2)e_{j_1m_1}e_{j_2m_2},; M=-J,-J+1,ldots,J.$

Они являются собственными векторами операторов момента ${bfhat J}^2$ и

(см. п. 7). Коэффициенты разложения C(j₁j₂JM|j₁j₂m₁m₂) называются коэффициентами Клебша-Гордана. Мы нашли их явный вид для частного случая j₁=j₂=1/2.
Введя дискретные спиновые переменные для электронов

, запишем найденные базисные векторы $chi_{S,zeta}$ в виде функций двух переменных:

$begin{array}{l} chi_{1,-1}(zeta_1,zeta_2)=d(zeta_1)d(zeta_2)=chi_{1,-1}(zeta_2,zeta_1), chi_{1,0}(zeta_1,zeta_2)=frac{1}{sqrt{2}}[u(zeta_1)d(zeta_2)+d(zeta_1)u(zeta_2)]=chi_{1,0}(zeta_2,zeta_1), chi_{1,1}(zeta_1,zeta_2)=u(zeta_1)u(zeta_2)=chi_{1,1}(zeta_2,zeta_1); chi_{0,0}(zeta_1,zeta_2)=frac{1}{sqrt{2}}[u(zeta_1)d(zeta_2)-d(zeta_1)u(zeta_2)]=-chi_{0,0}(zeta_2,zeta_1), end{array}$

При этом три симметричные функции $chi_{1,zeta}(zeta_1,zeta_2)$ образуют базис в пространстве D₁, а антисимметричная функция $chi_{0,0}(zeta_1,zeta_2)$ - в D₀.

Атом гелия

Применим полученные выше результаты для анализа общей структуры спектра атома гелия ⁴₂He - системы, состоящей из положительно заряженного ядра с Z=2 и двух электронов.
В приближении бесконечно тяжелого ядра гамильтониан атома гелия сводится к системе двух электронов, взаимодействующих между собой и с неподвижным кулоновским центром с зарядом -2e:

$hat H=-frac{hbar^2}{2m_e}(nabla_1^2+nabla_2^2)-2e^2left(frac{1}{r_1}+frac{1}{r_2}right)+frac{e^2}{r_{12}},$

где r₁₂=|r₁-r₂| - расстояние между электронами. Подчеркнем, что спиновые взаимодействия в нерелятивистском приближении не учитываются.
Решение стационарного уравнения Шредингера

можно искать в виде разложения по базисным спиновым функциям, найденным в предыдущем разделе:

$psi({bf r_1},zeta_1;{bf r_2},zeta_2)=sumlimits_{S,zeta}^{}varphi_{S,zeta}({bf r_1,r_2})chi_{S,zeta}(zeta_1,zeta_2).$

Из антисимметричности полной функции

и свойств симметрии спиновых функций

следует, что координатные функции обладают определенной симметрией:

$varphi_{1,zeta}({bf r_1,r_2})=-varphi_{1,zeta}({bf r_2,r_1}),; varphi_{0,0}({bf r_1,r_2})=varphi_{0,0}({bf r_2,r_1})$

т. е. принадлежат подпространству H_A(H_S) пространства L²(R⁶) при S=1 (S=0). Эти функции удовлетворяют тому же уравнению Шредингера, что и

$(hat H-E)varphi_{S,zeta}({bf r_1,r_2})=0,$

причем симметричная и антисимметричная функции принадлежат, очевидно, разным собственным значениям.
Таким образом, уровни энергии атома гелия зависят от полного спина S даже в пренебрежении спиновыми взаимодействиями в гамильтониане. Эта зависимость - следствие принципа тождественности и обусловлена свойствами симметрии координатных волновых функций.
Можно доказать, что основному состоянию атома гелия отвечает симметричная функция $varphi_{1,0}({bf r_1,r_2})$ , и спин S=0.
Переходы между состояниями с различными спинами с испусканием или поглощением фотонов оказываются маловероятными. В дипольном приближении вероятность перехода (см. п. 10) обращается в нуль, так как равен нулю матричный элемент оператора дипольного момента между состояниями различной симметрии:

$(varphi_A,({bf r_1+r_2})varphi_S)=int d^3 x_1 d^3 x_2 varphi^*_A({bf r_1,r_2})({bf r_1+r_2})varphi_S({bf r_1,r_2})equiv 0.$

Поэтому спектр излучения атома гелия таков, как если бы существовали две разновидности гелия - парагелий (S=0) и ортогелий (S=1). Уровни энергии ортогелия имеют трехкратное вырождение по спиновому числу

- проекции полного спина S_z (2S+1=3).
Замечание. Спиновые взаимодействия расщепляют триплетные уровни ортогелия (в отличие от синглетных уровней парагелия) на три близких подуровня (за исключением уровней, отвечающих нулевому полному орбитальному моменту системы двух электронов: L=0).

Обсуждение Еще не было обсуждений.

Последнее редактирование: 2018-04-19

Оценить статью можно после того, как в обсуждении будет хотя бы одно сообщение.

Об авторе:
Этот материал взят из источника в свободном доступе интернета. Вся грамматика источника сохранена.

Тест: А не зомбируют ли меня? Тест: Определение веса ненаучности

В предметном указателе: О картине мира и чем они обосн... | Основа личности | основные методы познания мира | Fornit Neurocomputer Искусственный интеллект, основы | Долг гражданский. Основные права и обязанности гражданина России | Ермолаев Д.С. Основная Цель Жизни субъекта | Законопроект о неподсудности священных писаний четырех основных религий — христианства, ислама, иудаизма и буддизма | Взаимодействие полей | Флуктуация вакуума | Ансамблевые интерпретации квантовой межаники в США и СССР | Квантовая запутанность | Квантовая логика физического вакуума | Квантовая механика | Квантовая механика М.Б.Менский | Концепция неопределённости квантовой механики | Отец Тимофей и Божественная механика Вселенной | А.В. Бялко, ТОРСИОННЫЕ МИФЫ | А.В.Рыков Вакуум и вещество Вселенной | Два способа расчета «плотности» тёмной материи А.В. Рыков | Для чего нужны сейсмографы? А.В.Рыков | Книги по медицине - ПАТОЛОГИЧЕСКАЯ ФИЗИОЛОГИЯ В ВОПРОСАХ И ОТВЕТАХ 488-end Атаман А.В. | Борис Жуков Неуловимая энграмма | Гравитационное взаимодействие Алеманов Сергей Борисович | Борис БОЛОТОВ | Обсуждение Борис БОЛОТОВ

Последняя из новостей: Трилогия: Основы фундаментальной теории сознания.

Все новости

Обнаружен организм с крупнейшим геномом
Новокаледонский вид вилочного папоротника Tmesipteris oblanceolata, произрастающий в Новой Каледонии, имеет геном размером 160,45 гигапары, что более чем в 50 раз превышает размер генома человека.

Все статьи журнала

Тематическая статья: Тема осмысления

Все тематические статьи

Рецензия: Рецензия на книгу Дубынина В.А. Мозг и его потребности. От питания до признания

Все рецензии

Топик ТК: Интервью с Константином Анохиным

Все топики ТК

	посетителей	заходов
сегодня:	0	0
вчера:	0	0
Всего:	23843	28308

Авторские права сайта Fornit