Fornit
   
 

Этот материал взят из оригинальной страницы,
адрес которой http://phys.web.ru/db/msg/1161649/ Список основных тематических статей >>

Этот документ использован в разделе "Теории мироздания"

Распечатать

Теория относительности

М.В.Сажин

Государственный Астрономический Институт
им. П.К.Штернберга, Москва.

Рецензенты: др. физ. мат. наук В.Е.Жаров,
др. физ. мат. наук К.В. Куимов.


Введение

Этот курс лекций читался студентам кафедры небесной механики, астрометрии и гравиметрии в Государственном астрономическом институте им. П. К. Штернберга Московского государственного университета. Специальная теория относительности (СТО) давно стала рабочим инструментом физики и астрономии. В частности, СТО используется для вычисления параметров ускорителей элементарных частиц, т.е. для физики СТО давно является теорией - инструментом аналогично теории электродинамики Максвелла и Лоренца. Как следствие, внедрение СТО в инженерные расчеты потребовало включение этого курса в число обязательных курсов для студентов физических специальностей. Курс по специальной теории относительности входит как часть в современную электродинамику и в Московском государственном университете преподаются как обязательный курс.

Общая теория относительности (ОТО) была востребована современной технологией сравнительно недавно, два десятилетия назад в высокоточной позиционной астрономии. Сейчас ОТО в приближении слабого гравитационного поля используется в высокоточной навигации (система космической навигации GPS, ГЛОНАСС). Формулы для редукции за эффекты ОТО приводятся во всех астрономических справочниках.

Однако в преподавании СТО и ОТО наблюдается некоторый пробел. Курсы, посвященные общей теории относительности, читаются студентам, желающим специализироваться по релятивистской астрофизике или космологии. Специального курса для студентов специализирующихся по астрометрии и небесной механике до сих пор не было.

Потребность учета эффектов специальной и общей теории относительности возникла, когда точность рядовых измерений стала превышать 1 секунду дуги. Современная точность измерений в астрометрии составляет доли миллисекунды дуги, поэтому требуется учет поправок специальной и общей теории относительности. Следовательно астрометристам такой курс совершенно необходим.

К началу 90$^x$ годов точность позиционных измерений значительно выросла в радиодиапазоне и в оптическом диапазоне. В радиодиапазоне рост точности угломерных измерений связан, прежде всего, с успехами радиоинтерферометров со сверхдлинными базами (РСДБ). Сейчас точность угломерных измерений в международной сети РСДБ равняется 0.25 миллисекунды дуги (mas), составляя для некоторого числа особо стабильных источников десятки микросекунд ($\mu as$) дуги. Успехи в области оптической астрономии связаны, в основном, с экспериментом "HIPPARCOS". При проведении этого эксперимента достигнута точность несколько миллисекунд дуги для более чем 100 000 звезд по обеим координатам $\alpha$, $\delta$.

Точность в 1 mas предполагает учет поправок общей теории относительности на уровне порядка $\sim 10^{-9}$. Эффекты ОТО, которые необходимо учитывать при редукции астрономических наблюдений, включают в себя эффекты т.н. первого постньютоновского порядка в солнечной системе. Переход к точности $\sim 10^{-12}$ потребует более тщательной редукции, а следовательно учет более высоких членов по степеням отношения характерной скорости к скорости света (основной малый параметр при постньютоновских вычислениях).

Успех эксперимента HIPPARCOS породил новые астрометрические проекты GAIA, SIM, FAME, DIVA, DARWIN и т.п. Одна из научных целей таких проектов - составить новые каталоги звезд объемом вплоть до миллиарда звезд и точностью измерений координат вплоть до 10 - 1 $\mu as$. Наличие таких каталогов будет значительно облегчать задачи астрономов других специальностей.

В России также существуют космические проекты, часть научных целей которых составляют высокоточные угломерные измерения. В частности, необходимо упомянуть радиоинтерферометр на орбите, что позволит значительно повысить точность измерений в радиодиапазоне, а также проект "ЛОМОНОСОВ", предполагающий измерения в оптическом дииапазоне.

Необходимость редукции за эффекты общей теории относительности - естественное требование космических экспериментов 21 века по астрометрии. Точность этих экспериментов будет уже такая, что они будут иметь смысл только при учете эффектов СТО и ОТО. Эффекты, связанные с кривизной пространства - времени в нашей солнечной системе, а также с нестационарной кривизной пространства - времени в нашей Галактике, будут основными эффектами, которые определяют точность измерений в будущих экспериментах.

В стандартных учебниках по СТО и ОТО мало уделяется внимания чисто астрономическим аспектам специальной и общей теории относительности. Все перечисленное выше, вызвало необходимость читать новый курс, посвященный теории относительности для астрономов.

Надо отметить, что по теории относительности существует большое количество прекрасных учебников. Не перечисляя все, упомянем два основных. Это прежде всего том II курса Л.Д.Ландау, Е.М,Лифшица, озаглавленный "Теория поля", а также книга С. Вайнберга "Гравитация и относительность". Методика преподавания теории относительности сейчас достаточно сильно зависит от того, студентам какой физической специальности читается соответствующий курс. Данный курс построен так, что изложение основных идей СТО и ОТО следует во многом историческому пути, который прошел сам А.Эйнштейн. Автор лекций постарался собрать воедино лучшие объяснения основных идей, которые лежат в основе теории относительности. В лекциях также уделено достаточно много внимания примерам, на которых демонстрируется применение идей и методов теории относительности.

Остается только добавить, что написание и издание этого материала стало возможным только благодаря поддержке грантов РФФИ N 00 - 02 - 16350. Автор также благодарен за большую работу, взятую на себя докт. физ.-мат. наук В.Е.Жаровым и докт. физ.-мат. наук К.В. Куимовым, которая заключалась в редактировании текста и исправлении ошибок, ответственность за наличие которых лежит целиком на авторе. Автор благодарен также общему редактору И.А.Герасимову, благодаря которому стало возможно издание этой книги.

Разделы

1. Принципы относительности

1.1 Принцип относительности Галилея

Первый принцип относительности (ПО) был сформулирован еще в эпоху Возрождения Г.Галилеем. ПО относился к механике и гласил: "Законы механики в системе координат, движущейся равномерно и прямолинейно в пространстве, имеют тот же вид, что и в системе координат, покоящейся в пространстве".

Из этого постулата можно сделать простой вывод, а именно: существует бесконечно много эквивалентных систем координат, называемых инерциальными и совершающими равномерное и прямолинейное движение или покоящихся друг относительно друга. В этих системах законы механики выполняются в простой классической форме.

Определим сразу, что законами механики здесь будем называть законы движения в классической механике и законы сохранения.

Принцип относительности Галилея на математическим языке преобразования координат обычно формулируется следущим образом. Пусть положение пробной частицы описывается в декартовой системе координат $K=\{x, y, z, t\}$, кроме трех пространственных координат мы добавили временную координату, которая необходима в специальной теории относительности (СТО) и общей теории относительности (ОТО), $t$. В системе координат $\hat K$= $\hat x$, $\hat y$, $\hat z$, $\hat t$, законы механики остаются неизменными, если система $\hat K$ движется относительно системы координат $K$ со скоростью $v$, так, что две системы координат связаны между собой преобразованием Галилея:


$\displaystyle \hat x=x-vt$ (1.1)
$\displaystyle \hat y=y$  
$\displaystyle \hat z=z$  
$\displaystyle \hat t=t$  

Рисунок 1.1: Здесь представлены оси $Ox$ и $Ot$ до преобразований Галилея и оси $O\hat x$ и $O\hat t$ после преобразований Галилея.
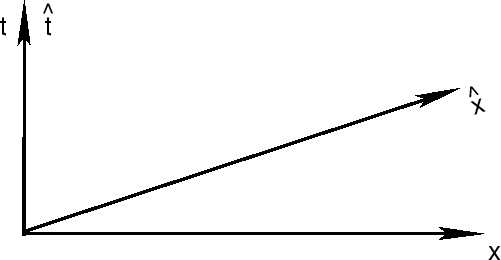\begin{figure}\centerline{\epsfxsize=0.7\textwidth\epsfbox{fig1_1.ai}}\end{figure}

В частности из принципа относительности Галилея вытекал закон сложения скоростей:
\begin{displaymath} \hat V=V-v \end{displaymath} (1.2)

здесь $\hat V$ скорость пробной частицы в системе $\hat K$, $V$ скорость этой же частицы в системе $K$, а $v$ скорость движения одной системы координат относительно другой, которая также входит в закон преобразования координат.

Законы механики остаются неизменными также в системах координат, оси которых повернуты друг относительно друга. Поскольку астрономы - наблюдатели с преобразованиями типа поворота имеют дело повседневно, обсудим их более подробно.

1.1.1 Вращения в трехмерном пространстве

На языке математики преобразования Галилея называются преобразованиями трехмерной системы координат. Преобразования типа (1.1) называются преобразованием сдвига. Помимо сдвига в трехмерном пространстве также часто используют преобразование вращения.

Рассмотрим все вращения трехмерного пространства вокруг одной фиксированной точки - начала координат. В ортогональной системе координат трехмерного пространства вращение задается уравнением
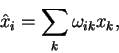\begin{displaymath} \hat x_i=\sum_{k} \omega_{ik} x_k, \end{displaymath} (1.3)

где $x_i$ -координаты вектора в системе $K$, $\hat x_i$ координаты того же вектора в системе $\hat K$. Матрица $\omega_{ik}$ определяет вращение. Будем обозначать вращение иногда буквой $\hat \omega$, той же, что и матрицу. Напишем несколько дополнительных условий на вращение. Так как вращение не меняет длин и углов между векторами, то оно не меняет и их скалярных произведений.

Кроме того, при вращении остается инвариантной форма вида:

\begin{displaymath} R^2=x_1^2 +x_2^2 +x_3^2 \end{displaymath}

Поэтому можно получить уравнение для коэффицентов матрицы вида:
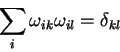\begin{displaymath} \sum_{i} \omega_{ik} \omega_{il} =\delta_{kl} \end{displaymath} (1.4)

где символом $\delta_{ik}$ называется число, равное 1, если $i=k$, и равное 0, если $i \ne k$.

Матрицы удовлетворяющие уравнению (1.4) называются ортогональными матрицами. Если вычислить детерминант обеих частей уравнения (1.4), то получим условие вида $ \left(Det(\hat \omega)\right)^2=1 $, что дает два возможных знака детерминанта:

\begin{displaymath} Det(\hat \omega)= \pm 1 \end{displaymath}

Знак $+$ соответствует собственным преобразованиям, знак $-$ соответствует несобственным преобразованиям. К несобственным преобразованиям относятся, например, отражения. Нам они не нужны и в дальнейшем рассматриваться не будут.

Рассмотрим вращения.

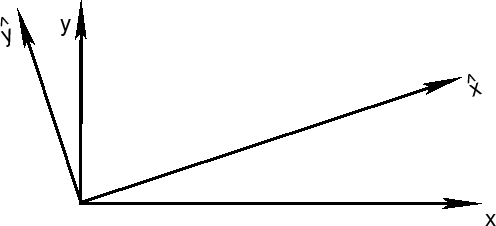
Прежде всего проанализируем две системы координат на плоскости. Одну систему координат будем обозначать $K$, вторую - $\hat K$. Будем считать, что центры этих систем совпадают, а оси повернуты друг относительно друга на угол $\varphi$ против часовой стрелки. Тогда преобразования от координат без крышечки к координатам с крышечкой записываются в виде системы линейных уравнений:

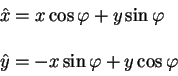
\begin{displaymath} \begin{array}{l} \hat x = x \cos \varphi + y \sin \varphi \\ \qquad \\ \hat y = -x \sin \varphi + y \cos \varphi \end{array}\end{displaymath}

Рисунок 1.2: Здесь представлены оси $Ox$ и $Oy$ до преобразований поворота и оси $O\hat x$ и $O\hat y$ после преобразований поворота.
\begin{figure}\centerline{\epsfxsize=0.7\textwidth\epsfbox{fig1_2.ai}}\end{figure}

Представим это преобразование в матричном виде. Как видно из предыдущей системы уравнений, вращения совершаются вокруг некоторой оси. Для начала выберем в качестве оси вращения ось $Oz$ и совершим вращение на угол $\varphi_1$. Матрица этого вращения имеет вид:


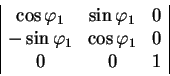
\begin{displaymath} \begin{array}{\vert ccc\vert} \cos \varphi_1 & \sin \varphi_... ... -\sin \varphi_1 & \cos \varphi_1 & 0 \\ 0 & 0 & 1 \end{array}\end{displaymath}

Детерминант такой матрицы равен единице.

Математики характеризуют вращение как некоторый вектор, направленный вдоль оси вращения и равный по величине углу поворота. Для астрономов более привычным является представление вращения в виде трех последовательных положительных вращений на углы Эйлера1.1. Рассмотрим их подробнее.

Полное вращение может быть представлено трех вращений. Первое - вращение $\omega_1$ 1.2на угол $\varphi_1$ вокруг оси $Oz$, в результате которого ось $Ox$ займет новое положение $Ox'$. Затем вращение $\omega_2$ вокруг новой оси $Ox'$ на угол $\theta$ в результате которого ось $Oz$ займет новое положение $Oz'$, и, наконец, вращение $\omega_3$ вокруг новой оси $Oz'$ в результате которого ось $Ox'$ вновь переместится на угол $\varphi_2$:


\begin{displaymath} \omega(\varphi_1, \theta, \varphi_2) = \omega(\varphi_1) *\omega(\theta) * \omega(\varphi_2) \end{displaymath} (1.5)

Элементы полной матрицы вращения $\omega(\varphi_1, \theta, \varphi_2)$ можно найти как произведение трех матриц поворотов вокруг осей $Oz$, $Ox'$, $Oz'$:
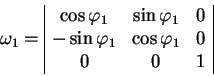\begin{displaymath} \omega_1= \begin{array}{\vert ccc\vert} \cos \varphi_1 & \si... ... -\sin \varphi_1 & \cos \varphi_1 & 0 \\ 0 & 0 & 1 \end{array}\end{displaymath} (1.6)


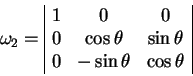\begin{displaymath} \omega_2= \begin{array}{\vert ccc\vert} 1 & 0 & 0 \\ 0 & ... ... & \sin \theta \\ 0 & -\sin \theta & \cos \theta \end{array}\end{displaymath} (1.7)


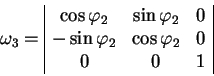\begin{displaymath} \omega_3= \begin{array}{\vert ccc\vert} \cos \varphi_2 & \si... ...-\sin \varphi_2 & \cos \varphi_2 & 0 \\ 0 & 0 & 1 \end{array}\end{displaymath} (1.8)

При перемножении матриц необходимо помнить, что они перемножаются в обратном порядке. Перемножив матрицы, получим:


$\displaystyle \omega=\omega_1 \times \omega_2 \times \omega_3= \phantom{\omega_1 \times \omega_2 \times \omega_3= }$ (1.9)
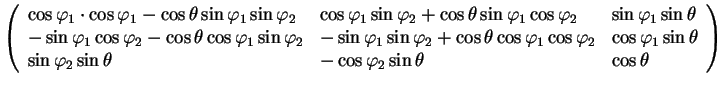$\displaystyle \left( \begin{array}{lll} \cos \varphi_1 \cdot \cos \varphi_1 -\c... ...hi_2 \sin \theta & -\cos \varphi_2 \sin \theta & \cos \theta \end{array}\right)$  

При вращениях углы $\varphi_1$ и $\varphi_2$ могут изменяться от 0 до $2\pi$, а угол $\theta$ от 0 до $\pi$. Различным тройкам чисел, которые изменяются в указанных пределах, соответствуют различные вращения, кроме случая $\theta=0$ и $\theta=\pi$. При $\theta=0$ вращение есть поворот вокруг оси $Oz$ на угол $\varphi_1 +\varphi_2$, а при $\theta=\pi$ вращение есть поворот вокруг оси $Oz$ на угол $\varphi_1 - \varphi_2$. Поэтому различным тройкам чисел $\varphi_1$, $\theta$, $\varphi_2$ может отвечать одно вращение.

Вращение (1.9) имеет обратный элемент. Обратный элемент - это вращение на такие углы, которые приводят систему координат в прежнее положение. Он задается другим вращением, которое совершается на углы Эйлера $\pi -\varphi_2$, $\theta$, $\pi -\varphi_1$.

Остается только добавить, что вращения образуют группу. Элементами группы являются повороты на углы Эйлера. Группа топологически эквивалентна шару, у которого отождествлены диаметрально противоположные точки.

1.1.2 Преобразования на момент наблюдения

В качестве примера приведем матрицу преобразования от координат небесных тел, заданных в каталогах к текущим координатам на данный момент наблюдений.

В каталогах обычно приводятся несколько характеристик некоторой звезды, две из которых - координаты звезды (ее положение) на небесной сфере $\alpha$ (прямое восхождение) и $\delta$ (склонение) приведенные на определенную эпоху. Другими словами, указывается положение звезды на определенный момент времени, скажем, на 1 января 2000 года. Кроме указания эпохи, необходимо определить саму систему координат и указать начало отсчета координат1.3.

Полюс мира - точка, на которую опирается полярная ось, вокруг которой вращается Земля - естественная ось для системы координат. Звезды в течении ночи меняют свое положение на небе (факт известный каждому, кто хоть раз наблюдал за ночным небом), лишь обна точка остается неподвижной - полюс мира. Наиболее близко к полюсу (но не точно в полюсе) находится Полярная звезда. Формально полярная ось определяется как ось, проведенная через центр системы координат, параллельная оси вращения Земли [1]. Перпендикулярно полярной оси лежит плоскость экватора.

В астрономии исторически выбирана сферическая система координат связанная с вращением Земли. Полярная ось и экватор служат основными элементами этой системы координат. Угол, который отсчитывается в плсокости экватора называется прямым восхождением, а угол, который отсчитывается вдоль меридиана от плоскости экватора называется склонением. Повторим, что такая система небесных координат возникла исторически в древнем мире и сохраняется в астрономии до сих пор.

Плоскость экватора (или положение полярной оси) определяет начало отсчета угла по склонению. Вторая основная точка системы координат, начало отсчета выбирается для того, чтобы указать точку от которой отсчитывается вращение Земли. Такая точка исторически была выбрана как точка пересечения небесного экватора и эклиптики. Экватор - плоскость перпендикулярная полярной оси и прекрасно подходит для задания угловой координаты. Кроме суточного вращения Земля испытывает еще и годовое вращение вокруг Солнца. В таком годовом вращении существует полюс эклиптики (ось орбиты Земли вокруг Солнца) и плоскость эклиптики, которая перпендикулярна полярной оси эклиптики. Экватор и эклиптика наклонены друг относительно друга на угол примерно $23^{\circ}27'$, точка пересечения используется для определения начала отсчета прямого восхождения. Остается добавить, что в математической физике, в сферической системе координат, прямое восхождение $\alpha$ обозначается обычно $\varphi$, эквивалентом второй астрономической координаты - склонения $\delta$ является сферическая координата $\theta={\displaystyle\pi\over\displaystyle 2} -\delta$.

Такое определение астрономической системы координат сохранялось в течение многих веков. В последнее десятилетие произошло существенное изменение. В 1991 г. Международный Астрономический Союз (МАС или IAU - английская абревиатура) принял новую астрономическую систему координат основанную на наблюдениях радиоисточников. Эту систему назвали ICRF 1.4. Это высокоточная система координат, достаточно сказать, что современная точность положений так называемых определяющих источников - десятки микросекунд дуги. По определению системы ICRF в качестве экватора выбирается плоскость, которая совпадает со средним экватором на эпоху J2000.0, а также в качестве полярной оси выбирается ось совпадающая с полярной осью каталога FK5. Таким образом, начало отсчета склонения определяется также от экватора новой системы. Несколько по другому определяется точка отсчета прямого восхождения. В соответствии с рекомендациями IAU начало отсчета по $\alpha$ теперь выбирается следущим образом. Оно выбирается как можно ближе к динамической точке весеннего равноденствия на эпоху J2000.0, хотя и другим способом. А именно, началом отсчета выбрано среднее положение 23 радиоисточников, входящих в список источников, определяющих ICRF. Причем в радиокаталогах, эти источники смещены так, чтобы прямое восхождение квазара 3C273 B совпадало с оптической координатой $\alpha$ этого квазара.

Звезды обладают собственным движением, поэтому их положения меняются, изменение положения характеризуется собственными движениями (угловыми скоростями звезд по небу). Помимо этого, индивидуального для каждой звезды движения, существует единое движение всей небесной cистемы. Это движение связано с изменением ориентации Земли в космическом пространстве. Существует по крайней мере три движения - прецессия, нутация и движения полюса Земли. Если первые два движения являются детеминированными и могут быть предсказаны с высокой степенью точности, то третье движение - движение полюса - является стохастическим. Независимо от природы этих движений они эквивалентны вращениям на некоторые углы Эйлера. Рассмотрим как это можно сделать.

Оси декартовой системы координат в некоторую текущую эпоху $T$ наблюдений можно определить через повороты осей той же декартовой системы координат по отношению к осям в другую эпоху соответствующую началу отсчета как
\begin{displaymath} \vec n_T= \hat N \hat P \vec n_{T_0} \end{displaymath} (1.10)

Здесь мы написали только матрицы соответствующие нутации $\hat N$ и прецессии $\hat P$. Вектора $\vec n_{T_0}$ и $\vec n_T$ обозначают единичные вектора в эпохи $T_0$ и $T$ соответственно. По соглашению в астрономии первый вектор $\vec n_{T_0}$ называют средним вектором (в эпоху $T_0$), а второй - $\vec n_T$ истинным единичным вектором в эпоху $T$. Эти определения "средний" и "истинный" используют также и для других астрономических терминов, определяя таким образом положения звезд, орты систем координат, небесный экватор, положение точки весеннего равноденствия, полюс и т.п.

Матрица прецессии $\hat P$ в уравнении (1.10) представляет вращение за счет общей прецессии за период времени $T-T_0$. Для правых экваториальных систем координат (первая ось направлена в точку весеннего равноденствия, третья ось перпендикулярна небесному экватору) вращение определяется тремя последовательными поворотами:
\begin{displaymath} \hat P= \hat R_3(-\varphi_3) \hat R_2(\theta) \hat R_3(-\varphi_1) \end{displaymath} (1.11)

Здесь матрицы $R_i$ являются вращениями вокруг оси $x_i$, так что
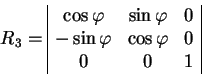\begin{displaymath} R_3= \begin{array}{\vert ccc\vert} \cos \varphi & \sin \varp... ...\\ -\sin \varphi & \cos \varphi & 0 \\ 0 & 0 & 1 \end{array}\end{displaymath} (1.12)

отметим, что по сравнению с математическим определением угла Эйлера $\varphi$ поворот здесь выбран в другую сторону.

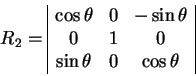
Отметим также поворот $R_2$ осуществляется не вокруг оси оси $Ox$, а вокруг оси $Oy$:
\begin{displaymath} R_2= \begin{array}{\vert ccc\vert} \cos \theta & 0 & -\sin ... ... \\ 0 & 1 & 0 \\ \sin \theta & 0 & \cos \theta \end{array}\end{displaymath} (1.13)

Углы $\varphi_1$, $\theta$, $\varphi_3$ являются функциями времени, они представляются в виде многочленов [1]:
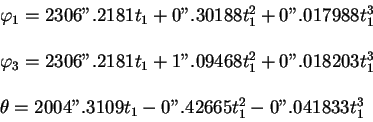\begin{displaymath} \begin{array}{l} \varphi_1=2306''.2181 t_1 +0''.30188 t_1^2 ... ...=2004''.3109 t_1 -0''.42665 t_1^2 -0''.041833 t_1^3 \end{array}\end{displaymath} (1.14)

Здесь $t_1=t$ - J2000.0 выражено в юлианских столетиях временной шкалы TDB (аббревиатура TDB означает динамическое барицентрическое время, поодробнее об определении различных сиистем времени в астрономии можно будет прочитать в книге В.Е.Жарова).

Матрица $\hat N$ представляет вращение обусловленное нутацией. Для экваториальной системы координат она задается следущим уравнением:
\begin{displaymath} \hat N=\hat R_1(-\varepsilon -\Delta \varepsilon) \hat R_3(-\Delta \psi) \hat R_1(\varepsilon) \end{displaymath} (1.15)

где $\varepsilon$ - средний наклон эклиптики, $\Delta \varepsilon$, $\Delta \psi$ - компоненты нутации по наклону и долготе. Наклон эклиптики к экватору $\varepsilon$ является функцией времени и вычисляется в виде многочлена.

Для преобразования координат от декартовой системы к экваториальной системе координат можно использовать, например, уравнение для единичного вектора указывающего направление на небесный источник:
\begin{displaymath} \vec n=(\cos \alpha \sin \delta, \sin \alpha \sin \delta, \cos \delta). \end{displaymath} (1.16)

Мы сделали только преобразование от средней системы координат к истинной экваториальной системе координат. Необходимо также сделать преобразование от истинной экваториальной системы координат к земной системе координат, в которой, собственно, и ведутся наблюдения. Для этого придется сделать преобразование вида:
\begin{displaymath} \vec n= \hat S \vec n_T \end{displaymath} (1.17)

здесь $\hat S$ - матрица описывающее суточное вращение Земли, в которую, кстати, входит и движение полюса, а $\vec n$ единичный вектор земной системы координат. Матрица $\hat S$ задается в виде произведения трех матриц - две из которых описывают движение полюса, а третья определяется часовым углом истинного весеннего равноденствия, которое отсчитывается от Гринвичского меридиана, этот часовой угол называется также истинным Гринвичским звездным временем (GAST). Параметры движения полюса отсчитываются относительно одной из осей условной земной системы координат.

Преобразования типа (1.10, 1.11, 1.15) определяют преобразования координат звезд от положений указанных в каталогах, на момент времени наблюдений. Как видно из приведенных уравнений, для высокоточных наблюдений типа РСДБ - наблюдений, приведение источников на место согласно уравнениям (1.10, 1.11, 1.15) является необходимым условием для успешных наблюдений, поскольку разница от эпохи один год уже приводит к значительному уходу небесного источника от положения указанного в таблиицах. Причем в случае РСДБ наблюдений производится редукция от земной системы координат к небесной системе.

Такие преобразования являются первым шагом на пути редукции небесных источников на истинное положение. Здесь они приведены для полноты. В дальнейшем приведение на истинное положение (редукция) будет обобщена на случай учета релятивистских поправок, которые изменять тривиальные уравнения типа (1.10, 1.11, 1.15).

1.2 Трудности классической механики при описании распространения света

Принцип относительности Галилея сыграл большую роль в создании механики как точной науки.

Физика развивалась, после механики были открыты законы оптики и создана теория электромагнитного поля. Был экспериментально открыт факт, что скорость света - самого быстрого движения в нашем мире не зависит от скорости движения источника света.

Этот факт явно противоречил закону сложения скоростей и принципу относительности Галилея. Более того, принцип относительности Галилея противоречил уравнениям электродинамики и электромагнитного поля.

Основная трудность, которую надо было преодолет путем применения принципа относительности к электродинамике, заключалась в том, что надо было согласовать два противоречящих друг другу утверждения:

  • Согласно классической механике скорость любого тела относительно двух наблюдателей двигающихся относительно друг друга разная.

  • Скорость света, согласно опыту, не зависит от движения наблюдателя или источника света и является мировой физической постоянной.

    Первое утверждение носило теоретический, концептуальный характер, тогда как второе было основано на опыте. Поскольку второе утверждение основано на опыте, то его ценность выше и следует отказаться отпервого утверждения и тем самым от тех представлений о пространстве и времени, которые были приняты ранее.

    Одно из представлений от которых мы отказываемся - ньютоновское понятие одновременности. Ньютон, постулируя существование абсолютного времени, или абсолютной длительности, писал: "время течет всегда одинаково, безотносительно к чему либо внешнему".

    В 1905 г. А.Эйнштейном был сформулирован принцип специальной относительности, который был справедлив для применения к теории электродинамики и теории электромагнитного поля и заложил новый взгляд на пространство и время.

    1.3 Специальная теория относительности

    В специальной теории относительности появляется новое определение понятия одновременности.

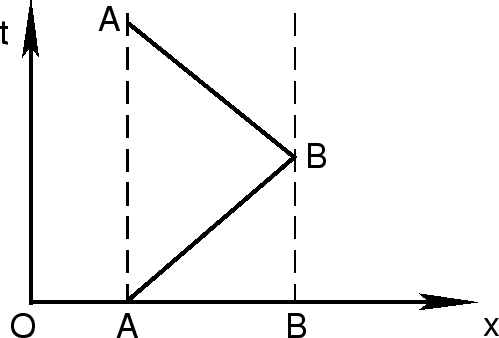
    Одновременность событий. Два события происходят в один и тот же момент времени синхронизированных часов в различных точках пространства. Возникает новое определение синхронизованных часов. Пусть в точках $A$ и $B$ есть часы. Определяем, что время прохождения света из $A$ в $B$ равно времени прохождения света из $B$ в $A$. Поясним это на рис. 1.3. Пусть в момент времени $t_A$ из $A$ посылается световой сигнал, он достигает точки $B$ в момент времени $t_B$, отражается и достигает точки $A$ в момент времени $t_A^0$. Часы по определению идут в точках $A$ и $B$ синхронно если
    \begin{displaymath}t_B -t_A= t_A^0 -t_B \end{displaymath} (1.18)

    Рисунок 1.3: На диаграмме $Otx$ изображен путь света от точки $A$ до точки $B$ и обратно
    \begin{figure}\centerline{\epsfxsize=0.7\textwidth\epsfbox{fig1_3.ai}}\end{figure}

    Принимаются также две аксиомы:

  • Если часы $B$ идут синхронно с часами $A$, то часы $A$ идут синхронно с часами $B$.

  • Если часы $A$ идут синхронно с часами $B$, а часы $B$ идут синхронно с часами $C$, то часы $A$ идут синхронно с часами $C$.

    А.Эйнштейн также сформулировал два принципа: принцип относительности и принцип постоянства скорости света.

    Принцип относительности
    Законы, по которым изменяются состояния физических систем, не зависят от того, к которой из двух координатных систем, движущихся друг относительно друга прямолинейно и равномерно, эти изменения относятся.

    Принцип постоянства скорости света
    Каждый луч света движется в избранной системе координат со скоростью $c$, независимо от того, испускается ли этот луч покоящимся или движущимся телом. При этом скорость луча света определяется согласно:

    Скорость света= ${\displaystyle\mbox{путь луча света}\over\displaystyle\mbox{промежуток времени}}$

    Несмотря на абстрактность эти определения особенно важны для интерпретации астрономических наблюдений. Продемонстрируем это утверждение на простом примере.

    1.3.1 Сверхсветовые движения и их интерпретация

    Некоторое время назад он представлял из себя загадку для сообщества астрономов, которая бросила вызов теории относительности.

    Рассмотрим рис. 1.4. Пусть из источника $S$ выбрасывается материя (например, сгустки плазмы). Эти сгустки летят под углом $\alpha$ к направлению на наблюдателя. Чему равна видимая поперечная скорость перемещения этих сгустков по небу?

    Рисунок 1.4: На рисунке изображено движение релятивистских выбросов из квазара.
    \begin{figure}\centerline{\epsfysize=0.5\textheight\epsfbox{fig1_4.ai}}\end{figure}

    Эта задача возникла при анализе т.н. сверхсветовых движений в квазарах. Из многих квазаров наблюдаются выбросы большого количества вещества. При наблюдениях выбросов астрономы измеряли их угловые скорости. По их красному смещению определялось расстояние до квазаров. Умножая расстояние до квазаров на угловую скорость перемещения выбросов по небу астрономы получали поперечную скорость движения выброса. Стандартная процедура дала неожиданный результат. В нескольких случаях поперечная скорость движения выбросов оказалась больше скорости света!

    Астрономы были поставлены перед нелегкой задачей. Казалось, что надо сделать выбор из двух, одинаково плохих вариантов. Первый - признать, что в природе могут существовать скорости больше, чем скорость света. Просто они не встречаются ни в солнечной системе, ни тем более в лабораторных условиях. Второй вариант - признать, что красное смещение в квазарах - не результат космологического красного смещения, а следовательно квазары могут быть расположены к нам гораздо ближе. Оба варианта, как я уже сказал были плохими.

    Однако, решение задачи оказалось возможным в рамках как специальной теории относительности, так и в рамках космологического сценария существования квазаров. Решение, найденное П.Шейером, основывалось на правильном обращении с понятием одновременности.

    Рассмотрим движение одного сгустка вещества. Пусть в момент времени $t=0$ он выбрасывается из источника $S$ под углом $\alpha$ к направлению $SO$. Сгусток представляет из себя плазму, излучающую радиоволны. Поэтому одновременно с выбросом сгустка, к наблюдателю по направлению $SO$ идет световой сигнал (фотоны радиочастоты) о том, что сгусток выброшен. Сгусток движется со скоростью $v$ и через некоторый интервал времени $t$ оказывается в положении $B$. К этому времени световой сигнал прошел путь $ct$ и оказался в точке $I$. Сгусток продолжает излучать радиофотоны. Поэтому через время $t$ из точки $B$ в направлении наблюдателя вновь идет сигнал о том, что сгусток достиг $B$. Построим вспомогательный перпендикуляр из $B$ на прямую соединяющую $S$ и $O$. Вычислим продольное расстояние $\Delta l$ между точками $A$ и $I$. Оно равняется:

    \begin{displaymath} l=ct -v t \cos \alpha \end{displaymath}

    Поперечное расстояние между точками $A$ и $B$ равняется величине:

    \begin{displaymath} l_t=vt\sin \alpha \end{displaymath}

    Угол между прямыми $OA$ и $OB$ ничтожно мал (мы считаем, что расстояние до квазара значительно превосходит все остальные масштабы рассматриваемой задачи). Поэтому сигналы о том, что сгусток вышел из источника $S$ и пришел в точку $B$ придут к наблюдателю через интервал времени $\tau=ct-vt\cos \alpha$, а поперечное расстояние пройденное этим сгустком будет составлять $l_t={\displaystyle v\over\displaystyle c}t\sin \alpha$. Теперь можно разделить поперечное расстояние на интервал времени между событие 1 (выход сгустка из источника) и событием 2 (появление сгустка в точке $B$) получаем видимую скорость перемещения сгустка по небу:

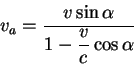
    \begin{displaymath} v_a={\displaystyle v\sin \alpha\over\displaystyle 1-{\displaystyle v\over\displaystyle c}\cos \alpha} \end{displaymath}

    Отсюдя видно, что когда скорость движения сгустка близка к скорости света, а угол $\alpha$ мал, видимая скорость движения сгустка по небу может значительно превышать скорость света.

    Рассмотрим подробнее условия при которых видимая скорость перемещения сгустка по небу будет превышать скорость света. Итак, будем считать, что
    \begin{displaymath} v_a>c. \end{displaymath} (1.19)

    Исходя из этого условия найдем в каких пределах должен меняться угол $\alpha$. Из условия (1.19) следует, что

    \begin{displaymath} \sin(\alpha +{\displaystyle\pi\over\displaystyle 4})>{\displaystyle c\over\displaystyle\sqrt{2}v} \end{displaymath}

    Поскольку тригонометрические функции не превышают 1, то появляется первое условие для скорости сгустка $v>{\displaystyle c\over\displaystyle\sqrt{2}}$. Второе условие выглядит как:

    \begin{displaymath} \alpha_{max} \approx {\displaystyle c\over\displaystyle v}-1 \end{displaymath}

    Значит, когда угол $\alpha$ находится в пределах 0 $ < \alpha <$ $\alpha_{max}$ наблюдатель видит сверхсветовое перемещение сгустка по небу.

    В этом примере сверхсветовое движение было объяснено без выхода за рамки специальной теории относительности. Здесь основную роль сыграло правильное обращение с понятием одновременных событий ( в данном случае одновременный приход сигналов к наблюдателю).

    3. Ускоренные системы отсчета >>

    Разделы

    2. Специальная теория относительности

    Астрономы наблюдают электромагнитное излучение (свет) небесных источников в различных диапазонах спектра. Хотя само излучение характеризуется целым набором параметров, для астрономии важны следущие: направление прихода света, его частота, а также иногда интенсивность. Для большинства астрономических задач волновая природа электромагнитного излучения также не играет решающей роли. Обычно большинство задач с успехом может быть решено в приближении геометрической оптики принимаемых фотонов, включая даже фотоны радиодиапазона. Лишь несколько задач требуют учета волновой природы, например, задачи интерферометрии. Однако, для вычисления многих задач интерферометрии достаточно знания только параметров излучения, найденных в пределе геометрической оптики. Поэтому мы будем работать с основным параметром характеризующими излучение в пределе геометрической оптики - волновым вектором излучения. Направление прихода лучей света и его частота в специальной теории относительности объединяются в единый вектор - 4$^x$ импульс фотона.

    Поэтому одной из основных наших задач будем вывод уравнений редукции и их решения для четырехмерного вектора импульса фотона.

    2.1 Кинематика специальной теории относительности

    Прежде чем выводить основные кинематические уравнения СТО сформулируем принцип постоянства скорости света на языке математики.

    Рассмотрим опять две системы, движущиеся равномерно и прямолинейно друг относительно друга. Будем считать, что система $K$ неподвижна относительно наблюдателя, а система $\hat K$ движется со скоростью $v$. Пусть в $K$ из точки с координатами $(x_1,$ $y_1,$ $z_1)$ в момент $t_1$ выходит луч света и достигает точки с координатами $(x_2,$ $y_2,$ $z_2)$ в момент $t_2$. В системе $\hat K$ эти два события выглядят следущим образом. В момент $\hat t_1$ из точки с координатами $(\hat x_1,$ $\hat y_1,$ $\hat z_1)$ выходит луч света, который попадает в точку с координатами $(\hat x_2,$ $\hat y_2,$ $\hat z_2)$ в момент времени $\hat t_2$.

    Из уравнений теории электромагнитного поля ( уравнений Максвелла) мы знаем, что пространственно - временная точка $(x_1,$ $y_1,$ $z_1$, $t_1)$ связана с пространственно - временной точкой $(x_2,$ $y_2,$ $z_2$, $t_2)$ равенством вида:
    \begin{displaymath} (x_1 -x_2)^2 + (y_1 -y_2)^2 +(z_1 -z_2)^2 =c^2 (t_1 -t_2)^2 \end{displaymath} (2.1)

    Здесь $c$ -скорость света. Постулат об одинаковости скорости света в обеих системах координат можно сформулировать так, что равенство (2.1) справедливо и в системе координат $\hat K$:
    \begin{displaymath} (\hat x_1 -\hat x_2)^2 + (\hat y_1 -\hat y_2)^2 +(\hat z_1 -\hat z_2)^2 =c^2 (\hat t_1 -\hat t_2)^2 \end{displaymath} (2.2)

    Обратим внимание, что в системе $\hat K$ уравнение содержит $c$, а не $\hat c$, поскольку две эти величины равны друг другу.

    Теперь будем считать, что точки 1 и 2 лежат бесконечно близко друг к другу, а также будем считать, что интервал времени для распространения света из 1 в 2 является бесконечно малым. Тогда упомянутые равенства можно записать как:
    \begin{displaymath} dx^2 + dy^2 +dz^2 =c^2 dt^2 \end{displaymath} (2.3)

    Введем теперь понятие 4$^x$ мерного интервала между двумя событиями. Будем называть первым событием то, которое произошло в точке с координатами $(x,$ $y,$ $z)$ в момент $t$, а вторым событием то, которое произошло в точке с координатами $(x+dx,$ $y +dy,$ $z +dz)$ в момент $t +dt$. Определим 4$^x$ мерный интервал между первым и вторым событием как расстояние в псевдоэвклидовом пространстве:
    \begin{displaymath} ds^2 =c^2 dt^2 -dx^2 - dy^2 -dz^2 \end{displaymath} (2.4)

    Из инвариантности скорости света следует, что интервал между двумя событиями - излучением света из какой -либо пространственной точки и приемом света в другой точке равен нулю в любой инерциальной системе отсчета. Т.е. $ds=0$ в системе $K$ и $\hat ds=0$ в системе $\hat K$.

    4$^x$ мерный интервал является инвариантом при преобразованиях координат, его величина не зависит от того в какой системах отсчета рассматриваются координаты между событиями. Воспользуемся этим свойством для вывода правильных преобразований координат между двумя системами, которые движутся относительно друг друга.

    2.1.1 Преобразования между инерциальными системами

    Рассмотрим две движущиеся системы координат. Из принципа постоянства скорости света, а также из инвариантности $4^x$ мерного интервала можно заключить, что в двух системах координат $K \in (t,x)$ и $\Xi \in (\tau, \xi)$, связанных линейными преобразованиями вида 2.1:
    $\displaystyle x=\xi \alpha +c\tau \beta$ (2.5)
    $\displaystyle ct= c \tau \alpha + \xi \beta$  

    должны совпадать дифференциалы интервала между двумя событиями:
    $\displaystyle ds^2= c^2dt^2- dx^2 \mbox{\hskip1cm в системе $K$}$ (2.6)
    $\displaystyle ds^2= c^2d\tau^2- d\xi^2 \mbox{\hskip1cm в системе $\Xi$}$  

    Коэффиценты преобразования $\alpha, \beta$ проще всего выбрать в виде:
    $\displaystyle \alpha=\ch \psi$ (2.7)
    $\displaystyle \beta =\sh \psi$  

    Рассмотрим дифференциалы (2.5) и подставим их в выражения для 4$^x$ мерного интервала. Легко видеть, что равенство

    \begin{displaymath} \ch^2 \psi -\sh^2 \psi=1 \end{displaymath}

    обеспечивает инвариантность интервала:

    \begin{displaymath} c^2dt^2-dx^2=c^2d\tau^2 -d\xi^2. \end{displaymath}

    Раасмотрим теперь связь угла $\psi$ в выражениях для гиперболических синуса и косинуса со скоростью системы $\hat K$ относительно системы $K$. Рассмотрим движение центра системы $\hat K$ в системе координат $K$. Центр системы координат $\Xi$ находится в точке $\xi=0$. В системе координат $K$ точка $\xi=0$ движется согласно системе уравнений:
    $\displaystyle x=c \tau \sh \psi$ (2.8)
    $\displaystyle ct= c \tau \ch \psi$  

    Отсюда легко заключить, что центр системы координат $\Xi$ движется в системе $K$ со скоростью:

    \begin{displaymath} {\displaystyle x\over\displaystyle ct}={\displaystyle v\over\displaystyle c}=\th \psi \end{displaymath}

    Теперь выражая гиперболические синус и косинус через гиперболический тангенс приходим к уравнениям для преобразования координат:
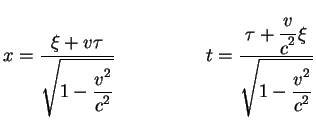    $\displaystyle x={\displaystyle\xi +v\tau\over\displaystyle\sqrt{1-{\displaystyl... ...le c^2}\xi\over\displaystyle\sqrt{1-{\displaystyle v^2\over\displaystyle c^2}}}$ (2.9)

    Отметим, что преобразования (2.9) больше похожи на преобразования типа вращения (1.3), а не преобразования Галилея (1.1). Рассмотрим теперь предел малых скоростей, когда ${\displaystyle v\over\displaystyle c} \ll 1$, разложим преобразования (2.9) в ряд Тэйлора по степеням этого малого параметра и оставим только линейные величины по ${\displaystyle v\over\displaystyle c} \ll 1$ пренебрегая квадратичными и более высокими степенями отношения взаимной скорости движения систем к скорости света:
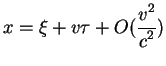    $\displaystyle x=\xi +v\tau +O({\displaystyle v^2\over\displaystyle c^2})$ (2.10)
    $\displaystyle \qquad$ (2.11)
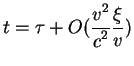    $\displaystyle t=\tau + O({\displaystyle v^2\over\displaystyle c^2}{\displaystyle\xi\over\displaystyle v})$ (2.12)

    Второй член в пребразовании времени выписан специально для того, чтобы продемонстрировать, что в преобразовании времени содержатся следы от преобразований Лоренца, но они второго порядка по отношению ${\displaystyle v\over\displaystyle c}$. Таким образом, преобразования Лоренца сводятся к преобразованиям Галилея. Поэтому в пределе малых (по сравнению со скоростью света) скоростей зависимость координаты $Ox$ от времени $\tau$ приобретает вид преобразования типа сдвига, время становится внешним параметром по отношению к преобразованиям трехмерных координат. Время становиться неизменным, внешнее влияние на этот параметр отсутствует.

    2.1.2 Интервал собственного времени

    Рассмотрим покоящуюся систему отсчета $K$. Рассмотрим в ней два события, скажем, колебание математического маятника, покоющегося относительно этой системы. Первое событие - прохождение маятника через точку равновесия, а второе - его повторное прохождение через равновесную точку. Пространственное расстояние между двумя событиями равно нулю $dx=0$, $dy=0$, $dz=0$. Тогда интервал между двумя этими событиями определяет интервал собственного времени $ds^2=c^2d\tau^2$.

    Это определение принятое в специальной теории относительности остается справедливым и в общей теории относительности.

    Рассмотрим теперь зависимость интервалов времени и длины от состояния движения. Пусть в системе $\hat K$ покоятся часы. Рассмотрим два события в системе $\hat K$. Первое событие - показание часов $\hat t_0=0$ в точке $\hat x=0$, $\hat y=0$, $\hat z=0$. Второе событие - показание часов $\hat t_1=1$ сек в той же точке пространства. Время в системе координат $\hat K$ между этими событиями есть $\tau =t_1- t_0=1$ сек. Интервал между этими событиями есть $ds=cd\tau=3\cdot 10^{10}$ см/сек $\times 1$ сек=300 000 км. Найдем время, которое прошло между этими событиями в системе $K$, в которой покоится наблюдатель измеренное по часом этого наблюдателя. Преобразование времени из системы $\hat K$ в систему $K$ осуществляется по формуле:

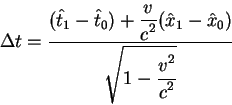
    \begin{displaymath} \Delta t={\displaystyle(\hat t_1 -\hat t_0) +{\displaystyle ... ...splaystyle\sqrt{1-{\displaystyle v^2\over\displaystyle c^2}}} \end{displaymath}

    поскольку пространственное расстояние в системе $\hat K$ между двумя событиями равно нулю, а интервал времени равен $\Delta \hat t=1$ сек, то в системе $K$ часы покажут, что прошло время:

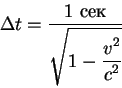
    \begin{displaymath} \Delta t={\displaystyle\mbox{1 сек}\over\displaystyle\sqrt{1-{\displaystyle v^2\over\displaystyle c^2}}} \end{displaymath}

    Итак, для наблюдателя, который покоится в системе координат $K$ часы показывают, что прошло больше времени, чем 1 сек. Это один из самых неожиданных выводов специальной теории относительности. Для неспециалистов этот вывод представлялся парадоксальным и послужил одним из поводов для попыток теоретически опровергнуть специальную теорию относительности, доказать ее внутреннюю противоречивость.

    Одним из наиболее распространенных способов опровергнуть СТО служил т.н. парадокс близнецов. Он формулировался следущим образом.

    Рассмотрим двух братьев - близнецов. Один из них улетает на ракете в длительное путешествие. Ракета двигается со скоростью близкой к скорости света, так что 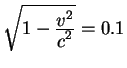$\sqrt{1-{\displaystyle v^2\over\displaystyle c^2}}=0.1$ Второй остается на Земле. Первый брат после путешествия возвращается на Землю. Его собственные часы показывают, что прошло, скажем, один год. Часы второго брата показывают, что прошло 10 лет. Вывод: брат - близнец живщий на Земле постарел на 10 лет, в то время как его брат - путешественник постарел только на один год.

    "Хорошо" - говорит желающий опровергнуть СТО. "Теперь давайте рассмотрим ситуацию с точки зрения брата - путешественника. С его точки зрения Земля движется со скоростью близкой к скорости света, а следовательно, на Земле часы должны идти медленнее. Брат - путешественник, вернувшись на Землю обнаружит, что у его брата - близнеца часы показывают только 365 дней."
    "Парадокс!"
    восклицает опровергатель,
    "Это доказывает внутреннюю противоречивость СТО!"
    После чего делается вывод, что СТО не верна.

    Разумеется, этот вывод основан на ошибке. Ошибка заключается в том, что космонавт, путешествующий на ракете, часть пути находится в неинерциальной системе отсчета. Поэтому две системы неэквивалентны. Доказано это будет, когда мы познакомимся с вычислением собственного времени в ускоренных системах отсчета. Пока же ограничимся указанием на то, что брат - близнец оставшийся на Земле, постареет больше чем путешественник.

    2.1.3 Длина движущегося стержня

    Рассмотрим теперь как меняются собственные длины стержней в движущейся и покоющейся системах отсчета.

    Для этого выпишем преобразование пространственной координаты (2.9) из движущейся в неподвижную систему:
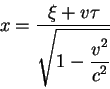    \begin{displaymath} x={\displaystyle\xi +v\tau\over\displaystyle\sqrt{1-{\displaystyle v^2\over\displaystyle c^2}}} \end{displaymath} (2.13)

    Размер стержня в неподвижной системе обозначим $x_1- x_0=l_p$. В покоящейся системе отсчета его размер определяется выражением:
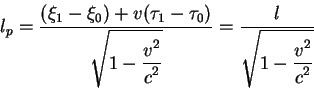    \begin{displaymath} l_p={\displaystyle(\xi_1 -\xi_0) +v(\tau_1-\tau_0)\over\disp... ...isplaystyle\sqrt{1-{\displaystyle v^2\over\displaystyle c^2}}} \end{displaymath} (2.14)

    поскольку размер стержня в движущейся системе $l$ необходимо определять в один и тот же момент времени $\tau_1=\tau_0$. Поэтому длина стержня будет максимальна в той системе отсчета в которой стержень покоится. В любой другой инерциальной системе отсчета, которая движется относительно покоящейся со скоростью $v$ длина стержня будет меньше:
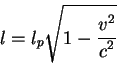    \begin{displaymath} l=l_p \sqrt{1-{\displaystyle v^2\over\displaystyle c^2}} \end{displaymath} (2.15)

    Пусть стержень длиной $l$ в собственной системе отсчета движется со скоростью $v$ относительно фотоаппарата далекого наблюдателя. За стержнем параллельно ему расположена линейка с нанесенными метками длины, которая покоится относительно наблюдателя. Направление на фотоаппарат составляет угол $\theta$ с направлением скорости стержня. Чему равна кажущаяся длина стержня? Какая часть мерной линейки закрыта стержнем?

    2.2 Общие преобразования системы координат, бусты.

    Рассмотрим теперь общие преобразования систем координат, которые включают в себя не только четырехмерные повороты связывающие ось времени и одну из пространственных осей, но также и трехмерные вращения. Такие общие преобразования позволяют сделать редукцию на момент наблюдений.

    Как и в параграфе посвященном обсуждению вращений рассмотрим линейное преобразование типа:
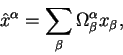    \begin{displaymath} \hat x^{\alpha}=\sum_{\beta} \Omega^{\alpha}_{\beta} x_{\beta}, \end{displaymath} (2.16)

    где $x_{\alpha}$ -координаты вектора в системе $K$, $\hat x_{\alpha}$ координаты того же вектора в системе $\hat K$. Матрица $\Omega_{\alpha \beta}$ определяет вращение. Будем обозначать вращение иногда буквой $\hat \Omega$, той же, что и матрицу. Кроме того, теперь координаты нумеруются буквами греческого алфавита и пробегают значения $\alpha \ni (0, 1, 2, 3)$. Всюду ниже будем придерживаться этого правила. Греческие буквы будут нумеровать четыре координаты (одну временную 0 и три пространственных 1, 2, 3), латинские (кроме специально оговоренных случаев) три пространственные координаты. В связи с этим греческие индексы будем иногда именовать пространственно - временнными, а латинские - пространственными индексами.

    Напишем несколько дополнительных условий на вращение. Теперь преобразования такого типа должны оставлять инвариантной четырех форму вида:
    \begin{displaymath} S^2=x_0^2 - x_1^2 -x_2^2 -x_3^2 \end{displaymath} (2.17)

    тогда такие преобразования называются преобразованиями Лоренца. Введем матрицу:
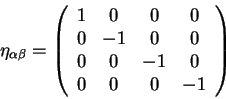    \begin{displaymath} \eta_{\alpha \beta}= \left( \begin{array}{cccc} 1& 0& 0& 0 \... ...1& 0& 0 \\ 0& 0& -1& 0 \\ 0& 0& 0& -1 \\ \end{array}\right) \end{displaymath} (2.18)

    при преобразованиях Лоренца имеет место равество

    \begin{displaymath} \hat \Omega^* \hat \eta \hat \Omega=\hat \eta \end{displaymath}

    здесь $\hat \Omega^*$ означает транспонированную матрицу. Отсюда легко заключить, что $Det(\eta)=\pm 1$, следовательно существует обратное преобразование $\hat \eta^{-1}$, которое также является преобразованием Лоренца. Произведение двух преобразований Лоренца также дает преобразование Лоренца, поэтому преобразования Лоренца образуют группу. Уравнение $S^2=x_0^2 - x_1^2 -x_2^2 -x_3^2 $ определяет в четырехмерном пространстве конус (его называют световым конусом). Световой конус делит все пространство - время на две внутренние полы конуса, в которых $S^2>0$ и внешние области, в которых $S^2<0$.

    Пусть $\hat \omega$ - матрица преобразования (вращение) трехмерного пространства. Рассмотрим преобразование в четырехмерном пространстве вида:

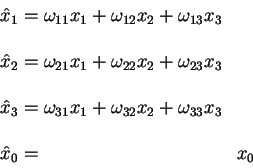
    \begin{displaymath} \begin{array}{l} \hat x_1=\omega_{11}x_1 +\omega_{12}x_2 +\o... ...mega_{31}x_1 +\omega_{32}x_2 +\omega_{33}x_3 +} x_0 \end{array}\end{displaymath}

    Это преобразование принадлежит группе преобразований Лоренца. Оно оставляет без изменения координату $x_0$ в сумме (2.17) и не меняет сумму $x_1^2 +x_2^2 +x_3^2$. Поскольку с каждым таким преобразованием можно отождествить вращение, то легко видеть, что трехмерные вращения образуют подгруппу преобразований Лоренца.

    Напишем матрицу поворота с учетом четвертой координаты:


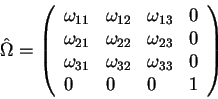    \begin{displaymath} \hat \Omega= \left( \begin{array}{llll} \omega_{11} & \omega... ... & \omega_{33} & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} \right) \end{displaymath} (2.19)

    Здесь в качестве элементов матрицы четырехмерных поворотов $\hat \Omega$ использованы элементы матрицы трехмерных поворотов $\hat \omega$.

    Рассмотрим теперь четырехмерные линейные преобразования типа (2.16). Отметим, что такие линейные преобразования являются преобразованиями типа вращения, но не преобразованиями типа сдвига. Для начала найдем преобразование связанное с вращением временной координаты.

    Преобразования связанные с преобразованиями Лоренца включающими временную координату, но исключающие вращения пространственных координат математики называют преобразованиями гиперболического поворота, а физики бустами, т.е. преобразованиями меняющими скорость системы координат.

    Рассмотрим преобразование в плоскости $(x_3, x_0)$. Такое преобразование не должно менять форму $x_0^2 -x_3^2$. Именно это преобразование математики называют иногда гиперболическим поворотом. Матрицу гиперболического поворота можно записать аналогично матрицам обычного поворота, заменив тригонометрическое косинус и синус на гиперболические косинус и синус:


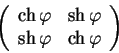
    \begin{displaymath} \left( \begin{array}{ccc} \ch \varphi & \sh \varphi \\ \sh \varphi & \ch \varphi \\ \end{array}\right) \end{displaymath}

    В четырехмерном виде эта матрица будет иметь вид


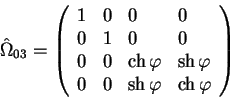    \begin{displaymath} \hat \Omega_{03}= \left( \begin{array}{llll} 1 & 0 & 0 & 0 ... ...\ 0 & 0 & \sh \varphi & \ch \varphi \\ \end{array} \right) \end{displaymath} (2.20)

    Подобным же образом будут выглядеть матрицы, которые описывают повороты в плоскостях $(x_1, x_0)$, $(x_2, x_0)$. Матрицу сложного поворота, описываемую как тригонометрическими функциями, так и включающую гиперболический поворот, описываемый гиперболическими функциями можно получить пользуясь теоремами сложения тригонометрических и гиперболических функций.

    Тем не менее в астрономии проще использовать преобразования Лоренца найденные в другом виде, который мы сейчас обсудим.

    Рассмотрим вновь общие преобразования Лоренца вида (2.16), но записанные для дифференциалов координат. Пусть система $\Xi$ покоится относительно наблюдателя, а система $K$ движется относительно него с произвольной скоростью $\vec v$.

    Преобразования описываются уравнением:
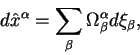    \begin{displaymath} d\hat x^{\alpha}=\sum_{\beta} \Omega^{\alpha}_{ \beta} d\xi_{\beta}, \end{displaymath} (2.21)

    У наблюдателя сопутствующего системе $\Xi$ меняется только время, которое является собственным временем этого наблюдателя. Дифференциалы пространственных координат этого наблюдателя в системе $\Xi$ равны нулю, поскольку координаты неизменны. Поэтому вектор описывающий изменение дифференциалов наблюдателя есть $(d\tau, 0, 0, 0)$. В системе $K$ дифференциалы наблюдателя есть:
    $\displaystyle d\hat x^i= \Lambda^i_0 d\tau,$ (2.22)
    $\displaystyle \qquad$ (2.23)
    $\displaystyle d t = \Lambda^0_0 d \tau . \nonumber$  

    Отношение 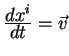${\displaystyle d x^i\over\displaystyle d t}=\vec v$ определяет скорость движения координатных систем друг относительно друга. Поэтому можно записать равенство:
    \begin{displaymath} \Lambda^i_0= {\displaystyle v^i\over\displaystyle c} \Lambda^0_0 \end{displaymath} (2.24)

    Напомним, что $x^0=ct$. Выведем второе уравнение для связи $\Lambda^i_0$ и $\Lambda^0_0$. Для этого вычислим интервал между событиями разделяемыми дифференциалами $d\xi^{\alpha}$ в системе $\Xi$ и дифференциалами $d x^{\alpha}$ в системе $K$. Тогда можно записать уравнение вида:
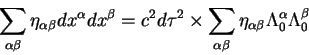    \begin{displaymath} \sum_{\alpha \beta} \eta_{\alpha \beta} d x^{\alpha} d x^{\b... ...eta} \eta_{\alpha \beta} \Lambda^{\alpha}_0 \Lambda^{\beta}_0 \end{displaymath} (2.25)

    Отсюда легко найти (поскольку в системе сопутствующей наблюдателю справедливо равенство $ds^2=c^2d\tau^2$), что:
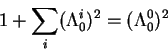    \begin{displaymath} 1 +\sum_i (\Lambda^i_0)^2 = (\Lambda^0_0)^2 \end{displaymath} (2.26)

    Теперь подставляем в уравнение (2.26) уравнение определяющие различные элементы матрицы буста через скорости (2.24) и получаем уравнения для определения элементов матрицы $\hat \Omega$:
    $\displaystyle \Lambda^0_0=\gamma,$ (2.27)
    $\displaystyle \vphantom{\Omega^0_0=\gamma}$  
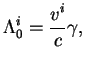    $\displaystyle \Lambda^i_0={\displaystyle v^i\over\displaystyle c} \gamma,$  

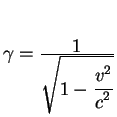    где $\gamma={\displaystyle 1\over\displaystyle\sqrt{1-{\displaystyle v^2\over\displaystyle c^2}}}$.

    Уравнения (2.25, 2.26) являются следствием более общего уравнения:
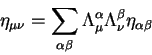    \begin{displaymath} \eta_{\mu \nu}=\sum_{\alpha \beta} \Lambda^{\alpha}_{\mu} \Lambda^{\beta}_{\nu} \eta_{\alpha \beta} \end{displaymath} (2.28)

    Пользуясь этим уравнение можно найти элементы матрицы $\hat \Omega$ с двумя пространственными индексами. Следует, однако, сразу сказать, что элементы этой матрицы определяются неоднозначно. Они всегда могут быть умножены на матрицу трехмерного вращения.

    Выберем вид трехмерных элементов четырехмерной матрицы вращения как:
    \begin{displaymath} \Lambda^i_j=\delta^i_j -v^i v_j {\displaystyle\gamma -1\over\displaystyle v^2} \end{displaymath} (2.29)

    Заметим, что векторные компоненты с нижними индексами отличаются знаком от векторных компонент с верхними индексами $v_j=\eta_{j i}v^i$.

    Произвольное преобразование Лоренца может быть выражено как произведение трехмерного вращения с бустом, который описывается матрицей $\Lambda^{\mu}_{\nu}$. Доказательство этого утверждения выходит за рамки курса, но читатель, знакомый с теорией групп легко воспроизведет его. Представим произвольное преобразование Лоренца в виде:
    \begin{displaymath} \Omega^{\mu}_{\nu}=\Lambda^{\mu}_{\alpha}\omega^{\alpha}_{\nu} \end{displaymath} (2.30)

    В таком виде преобразования Лоренца легко применять для получения уравнений редукции.

    2.3 Преобразования векторов

    Из курса линейной алгебры известно, что при преобразованиях вида (2.21) вектора преобразуются как
    \begin{displaymath} A^{\mu}=\Omega^{\mu}_{\nu} A^{\nu} \end{displaymath} (2.31)

    Кроме этого, общего, уравнения можно также привести еще несколько уравнений, которые являются очень полезными при выводе уравнений редукции, хотя они обладают меньшей общностью, чем (2.31). Одним из таких уранений является скалярное произведение векторов. Скалярное произведение двух векторов:

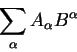
    \begin{displaymath} \sum_{\alpha} A_{\alpha}B^{\alpha} \end{displaymath}

    является инвариантом координатных преобразований. Докажем это для линейных преобразований вида (2.21). Пусть вектора $A_{\alpha}$ и $B^{\alpha}$ заданы в системе $\Xi$, сделаем преобразование вида (2.21) к новой системе координат $K$, которая движется со скоростью $\vec v$ относительно системы $\Xi$, кроме того, оси системы $K$ повернуты относительно первой системы в произвольном направлении, которое характеризуется тремя углами Эйлера. Теперь вычислим компоненты векторов $A_{\alpha}$ и $B^{\alpha}$ в новой системе $K$:

    \begin{displaymath} \hat A_{\mu}=\Omega_{\mu}^{\alpha} A_{\alpha}, \end{displaymath}

    и


    \begin{displaymath} \hat B^{\mu}=\Omega^{\mu}_{\alpha} B^{\alpha} \end{displaymath}

    Скалярное произведение векторов в системе $K$ выражается через произведение векторов в системе $\Xi$ с матрицами преобразования:

    \begin{displaymath} \hat A_{\alpha} \hat B^{\alpha}= \Omega_{\alpha}^{\beta}\Omega_{\gamma}^{\alpha} A_{\beta} B^{\gamma} \end{displaymath}

    Прямым вычисление произведения мариц можно показать, что
    \begin{displaymath} \Omega_{\alpha}^{\beta}\Omega_{\gamma}^{\alpha} =\delta^{\beta}_{\gamma} \end{displaymath} (2.32)

    Здесь $\delta^{\alpha}_{\beta}$ - символ Кронекера или единичная матрица2.2:


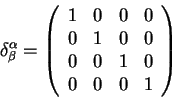    \begin{displaymath} \delta^{\alpha}_{\beta}= \left( \begin{array}{cccc} 1& 0& 0&... ...& 1& 0& 0 \\ 0& 0& 1& 0 \\ 0& 0& 0& 1 \\ \end{array}\right) \end{displaymath} (2.33)

    Подставим (2.33) в (2.32) и полчим, что скалярное произведение векторов в двух системах координат равно друг другу. Это и означает, что скалярное произведение является инвариантом при преобразованиях Лоренца. Заметим сразу, что скалярное произведение является инвариантным при любых, даже нелинейных преобразованиях. Доказательство этого утверждения отложим до пятой лекции.

    Кроме векторов нам иногда придется производит вычисления с объектами более сложной природы - тензорами и тензорными плотностями.

    Тензор второго ранга эквивалентен четырехмерной квадратной матрице $A^{\alpha \beta}$. Этот тензор преобразуется согласно правилу:

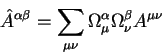
    \begin{displaymath} \hat A^{\alpha \beta} =\sum_{\mu \nu} \Omega^{\alpha}_{\mu} \Omega^{\beta}_{\nu} A^{\mu \nu} \end{displaymath}

    в случае, когда надо преобразовать тензоры второго ранга с двумя нижними индексами или с одним верхним и одним нижнем индексами необходимосуммировать их с $\hat \Omega$ матрицами с двумя верхними индексами суммирования или со смешанными индексами суммирования.

    Тензоры более высокого ранга при преобразованиях содержать больше произведений матриц $\hat \Omega$. тензоры третьего ранга три матрицы, тензоры четвертого ранга - четыре и т.п.

    2.4 Четырехмерная скорость

    Кинематические и динамические величины в четырехмерном пространстве отличаются от соответствующих трехмерных величин. Вначале определим четырехмерную скорость.

    Обычная трехмерная скорость определяется как отношение пройденного пути на промежуток времени, за который этот путь пройден:

    \begin{displaymath} \vec v={\displaystyle d \vec r\over\displaystyle dt} \end{displaymath}

    Из этой формулы видно, что для определения скорости в трехмерном пространстве используется внешний по отношению трехмерному пространству параметр - время. Если мы построим траекторию пробной частицы в трехмерном пространстве в виде трех функций времени, которые есть:


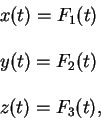
    \begin{displaymath} \begin{array}{l} x(t)=F_1(t)\\ \qquad\\ y(t)=F_2(t)\\ \qquad\\ z(t)=F_3(t), \end{array}\end{displaymath}

    то скорость можно определить также как касательный вектор

    \begin{displaymath} \vec v =({\displaystyle d x(t)\over\displaystyle dt}, {\disp... ...displaystyle dt}, {\displaystyle d z(t)\over\displaystyle dt}) \end{displaymath}

    к этой траектории.

    По аналогии с этим определением определяют четырехмерную скорость как вектор, касательный к четырехмерной траектории частицы. В качестве параметра вдоль траектории выбирают некоторый афинный параметр. Для частиц, которые обладают массой и движутся со скоростью меньше чем скорость света в качестве афинного параметра вдоль траектории обычно выбирают интервал:


    \begin{displaymath} u^{\mu}={\displaystyle d x^{\mu}\over\displaystyle d s} \end{displaymath} (2.34)

    Отметим важное отличие четырехмерной скорости, определенной согласно (2.34) от трехмерной скорости. Абсолютная величина трехмерной скорости является произвольной величиной. Абсолютная величина четырехмерной скорости равна единице.
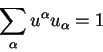    \begin{displaymath} \sum_{\alpha} u^{\alpha} u_{\alpha}=1 \end{displaymath} (2.35)

    В случае, когда мы рассматриваем пробную частицу, которая движется со скоростью света (например, фотон), то в качестве параметра вдоль траектории выбирают другой афинный параметр, например, путь, пройденный фотоном. Четырехмерный интервал вдоль траектории частицы движущейся со скоростью света уже выбирать нельзя, поскольку он равен нулю.

    Приведем явный вид четырехмерной скорости через трехмерную:
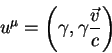    \begin{displaymath} u^{\mu} =\left( \gamma, \gamma {\displaystyle\vec v\over\displaystyle c}\right) \end{displaymath} (2.36)

    Приведем также уравнение для редукции волнового вектора фотона к наблюдателю. Для этого воспользуемся тем свойством, что векторное произведение волнового вектора фотона $k^{\mu}$ и четырехмерной скорости наблюдателя является инвариантной величиной
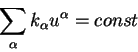    \begin{displaymath} \sum_{\alpha} k_{\alpha} u^{\alpha} =const \end{displaymath} (2.37)

    Инвариантность относительно преобразования системы координат означает, что $const$ не меняет своего значения при переходе от, скажем, покоющейся системы координат, к движущейся. Рассмотрим некоторого наблюдателя $O$ и его четырехмерную скорость $u^{\alpha}_O$. В системе координат сопутствующей наблюдателю вектор скорости принимает значение

    \begin{displaymath} u^{\alpha}_O = (1, 0, 0, 0) \end{displaymath}

    Соответственно скалрное произведение двух четырехмерных векторов вырождается в произведение двух величин: нулевой компоненты волнового вектора фотона и нулевой компоненты четырехмерной скорости. Поскольку второй сомножитель равен единице, то остается только одна величина $k_0$ компонента волнового вектора фотона. Эта компонента отождествляется с наблюдаемой частотой фотона (или с энергией фотона в системе координат, сопутствующей наблюдателю) $\nu_O$. Таким образом определяется значение $const$, которая стоит в правой части уравнения (2.37).

    Значение константы в правой стороне равенства (2.37), разумеется, будет другим для другого объекта. Рассмотрим в качестве другого тела источник фотонов. Вычислим правую часть (2.37) в системе координат, которая сопутствует источнику. Теперь константа в правой стороне равенства будет определять частоту излучения $\nu_E$. Естественно, что величина константы будет уже другая.

    Cоставим теперь отношение двух величин. Числитель этого отношения - произведение четырехмерной скорости источника фотонов на волновой вектор фотона. Знаменателем является скалярное произведение четырехмерной скорости наблюдателя в системе координат ему сопутствующей.
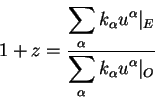    \begin{displaymath} 1+z={\displaystyle\sum_{\alpha} k_{\alpha} u^{\alpha}\vert _... ...er\displaystyle\sum_{\alpha} k_{\alpha} u^{\alpha}\vert _O } \end{displaymath} (2.38)

    Здесь индекс $O$ означает "наблюдатель", а индекс $E$ означает "излучатель". Величина $z$ обычно называется красным смещением, она пришла в релятивистскую теорию из космологии, в космологии это один из основных параметров, который характеризует источник.

    Поскольку справа стоит отношение двух констант, которые мы уже вычислили, то напишем это отношение явно:
    \begin{displaymath} {\displaystyle\nu_E\over\displaystyle\nu_O} = 1 +z \end{displaymath} (2.39)

    Теперь для того, чтобы вычислить частоту фотона, которую будет измерять наблюдатель, поступим следущим образом. В системе координат, сопутсвующей наблюдателю, волновой вектор фотона имеет компоненты


    \begin{displaymath} k_{\mu}= 2 \pi \nu_O\left(1, \vec n \right), \end{displaymath}

    здесь $\vec n$ -вектор в направлении излучения фотона. Все величины вычислены в системе координат сопутствующей наблюдателю.

    Излучатель имеет четырехмерную скорость

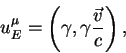
    \begin{displaymath} u^{\mu}_E =\left( \gamma, \gamma {\displaystyle\vec v\over\displaystyle c}\right) , \end{displaymath}

    где $\vec v$ -трехмерная скорость источника фотонов относительно наблюдателя.

    Скалярное произведение в системе координат наблюдателя есть
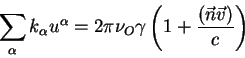    \begin{displaymath} \sum_{\alpha} k_{\alpha} u^{\alpha}=2 \pi \nu_O \gamma \left( 1 +{\displaystyle(\vec n \vec v)\over\displaystyle c}\right) \end{displaymath} (2.40)

    Теперь получаем, что отношение частоты излучателя к частоте того же фотона в системе наблюдателя есть:
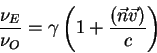    \begin{displaymath} {\displaystyle\nu_E\over\displaystyle\nu_O} = \gamma \left( 1 +{\displaystyle(\vec n \vec v)\over\displaystyle c}\right) \end{displaymath} (2.41)

    Это есть закон Допплера в специальной теории относительности.

    Рассмотрим уравнение (2.41) более подробно.

    Будем считать, что источник фотонов и наблюдатель находятся на оси $Ox$ и источник движется вдоль этой оси. Пусть излучатель движется по направлению к наблюдателю. Тогда $(\vec n \vec v)= -v$ и наблюдаемая частоты больше частоты излучателя:

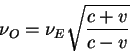
    \begin{displaymath} \nu_O = \nu_E \sqrt{{\displaystyle c + v\over\displaystyle c - v}} \end{displaymath}

    Частота фотонов смещается в голубую сторону спектра, мы имеем дело с голубым смещением.

    В том случае, когда направление распространения фотонов противоположно движению источника $(\vec n \vec v) = v$ возникает эффект красного смещения частоты:

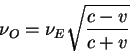
    \begin{displaymath} \nu_O = \nu_E \sqrt{{\displaystyle c - v\over\displaystyle c + v}} \end{displaymath}

    Рассмотрим еще один любопытный пример. А именно, под каким углом к направлению распространения фотонов должен двигаться источник, чтобы смещение частоты отсутствовало? Итак, на языке математики эту задачу можно сформулировать следущим образом: Найти такое значение 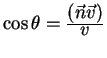$\cos \theta = {\displaystyle(\vec n \vec v)\over\displaystyle v}$ при условии $v \ne 0$, для которого $\nu_O = \nu_E$.

    Из условия равенства частот получаем, что косинус угла между направлением движения источника фотонов и направлением на наблюдателя есть:

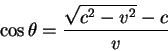
    \begin{displaymath} \cos \theta = {\displaystyle\sqrt{c^2 - v^2} - c\over\displaystyle v} \end{displaymath}

    Из приведенного уравнения видно, что эффект смещения частоты может отсутствовать лишь для источника удаляющегося от наблюдателя.

    Уравнение (2.41) описывает изменение частоты при переходе от движущегося источника к неподвижному наблюдателю. В реальности обычно источник фотонов и наблюдателя разделяет некоторое расстояние. Изменение частоты фотона при рапространении формула (2.41) не описывает. Если в пространстве между источником фотонов и наблюдателем присутствует, например, гравитационное поле, то появляется дополнительное изменение частоты, которое должно быть учтено.

    4. Эксперименты по ОТО >>

    Разделы

    3. Ускоренные системы отсчета и СТО

    Успех специальной теории относительности, правильное формулирование принципа относительности для инерциальных систем отсчета движущихся со скоростями близкими к скорости света побудил А.Эйнштейна на распространение этого принципа на ускоренные системы отсчета.

    Теперь вкратце расскажем как А.Эйнштейн смог описать ускоренные системы отсчета в терминах принципа относительности, как стало понятно, что это описание приводит к геометрической трактовке гравитационного поля, необходимости введения неэвклидовой геометрии в физику и идеи искривленного пространства - времени. Основная идея стала понятной А.Эйнштейну в 1907 г., хотя в оригинальном виде она была опубликована только в 1972 г. в газете "New York Times". Это идея позже получила название релятивистского принципа эквивалентности Эйнштейна. Сам А.Эйнштейн описал то время и мысли в отрывке, который помещен ниже. Перевод этого на русский язык слишком красив, чтобы его опустить:

    " Я пытался модифицировать теорию гравитации Ньютона таким образом, чтобы она точно соответствовала специальной теории относительности. Попытки сделать это показали, что теория гравитации может быть согласована с принципами специальной теории относительности, но они не удовлетворяли меня, поскольку требовали введения гипотез не содержащих физических основ. В это время ко мне пришла счастливейшая идея моей жизни 3.1 в следущем виде:
    Точно также, как электрическое поле создается электромагнитной индукцией, гравитационое поле может существовать только относительно. Следовательно, для наблюдателя, находящегося в свободном падении с крыши дома, гравитационного поля не существует ( по крайней мере в бесконечно близкой его окрестности ) в течении всего времени падения. Если наблюдатель выпустит из рук какие - либо предметы они остануться относительно этого наблюдателя в состоянии покоя независимо от их химического состава или физического состояния 3.2. Наблюдатель в этом случае должен признать, что он находится в состоянии покоя.

    Чрезвычайно интересный эмпирический закон гласящий, что все тела в одном и том же гравитационном поле падают с одним и тем же ускорением, получал в этом случае глубокий физический смысл. Если бы нашелся хотя бы один предмет, который падал бы в гравитационном поле не так как другие, то наблюдатель сравнивая свое движение с движением этого предмета смог бы сказать, что он находится в гравитационном поле и что он падает под его воздействием. Но если такого предмета не существует, а эксперимент подтверждает этот факт с большой степенью точности, наблюдатель теряет всякое объективное основание рассматриваться свое состояние как состояние падения в гравитационном поле. Скорее он имеет право рассматривать свое состояние как состояние покоя и считать, что в его ближайшем окружении гравитационное поле отсутствует.

    Таким образом, известный экспериментальный факт, что ускорение в гравитационном поле не зависит от химического состава или физического состояния становится могучим аргументом для распространения принципа относительности на координатные системы, которые движутся неравномерно одна относительно другой."

    3.1 Включение гравитации в СТО.

    Рисунок 3.1: На рисунке изображен лифт, в котором ускорение моделирует поле тяжести.
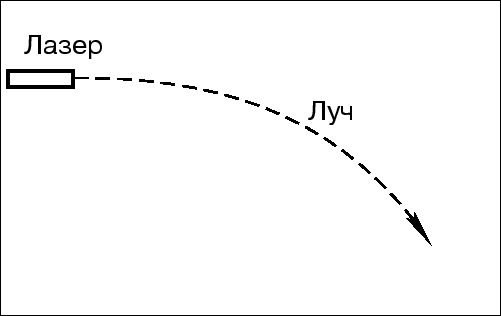    \begin{figure}\centerline{\epsfxsize=0.7\textwidth\epsfbox{fig3_1.ai}}\end{figure}

    Рассмотрим на рис. 3.1 пояснения к принципу эквивалентности Эйнштейна, который распространяет принцип относительности на ускоренные системы координат.

    На левом рисунке изображен лифт, ускоряемый вверх с величиной ускорения равной $a$. Свет, изображенный на рисунке пунктриной линией движется в таком лифте по искривленной траектории. Эта искривленная траектория является идеально прямой линией, но в покоящейся системе отсчета. В ускоренной системе отсчета линия становится искривленной. На правом рисунке изображен тот же самый лифт, который находится в поле тяжести с однородным ускорением. Принцип относительности примененный к ускоренным системам отсчета гласит, что невозможно отличить две этих ситуации. Значит, в лифте, который находится в гравитационном поле свет тоже должен двигатся по искривленной траектории.

    Вычислим характеристики света при движении в однородном поле тяжести пользуясь характеристиками света в ускоренном лифте. Для этого рассмотрим фотоны, которые распространяются вдоль поля тяжести $\vec g$. Это гравитационное поле исходя из принципа эквивалентности можно заменить полем ускорения с равной величиной, но противоположным знаком. Рассмотрим лазер $L$, который излучает фотоны с частотой $\nu_0$ (эта частота измеряется наблюдателем, находящимся рядом с лазером, т.е. сопутствующего лазеру). На расстоянии $l$ от лазера (по направленнию движения) находится другой наблюдатель $O$, который тоже измеряет параметры света. 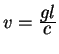Свет, который вышел из лазера в момент времени $t=0$ достигнет наблюдателя $O$ в момент времени $t={\displaystyle l\over\displaystyle c}$, а сам наблюдатель будет иметь скорость относительно лазера равную $v={\displaystyle gl\over\displaystyle c}$.

    Рассмотрим теперь две дополнительные инерциальные системы координат, которые двигаются равномерно и прямолинейно, так что ускорение в этих системах равно нулю. В первой системе координат $K_1$ в начале системы находится наблюдатель $O_1$. Скорость и положение этой системы выбраны так, чтобы в момент врмени $t=0$ наблюдатель $O_1$ находился в бесконечно малой окрестности точки $L$ ускоренной системы координат. Вторая инерциальная система движется со скоростью $v$ относительно первой так, чтобы в момент времени $t={\displaystyle l\over\displaystyle c}$ ее начало, в котором нахордится наблюдатель $O_2$ совпало с положением наблюдателя $O$, находящегося в ускоренной системе координат.

    Привлечение дополнительных инерциальных систем координат сделано не для того, чтобы запутать студента, а для того, чтобы провести расчеты характеристик света пользуясь уже знакомыми формулами специальной теории относительности.

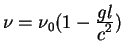
    Частота фотона измеренная наблюдателем $O_1$ в момент времени $t=0$ есть $\nu_0$, согласно нашему определению. В момент времени $t$ частота того же фотона, измеренная наблюдателем $O_2$, движущемся со скоростью $v$ относительно $O_1$ есть $\nu=\nu_0(1-{\displaystyle gl\over\displaystyle c^2})$

    Лазер представляет из себя стандартный электромагнитный осциллятор с собственнолй частотой $\nu_0$ и с периодом $P_0={\displaystyle 1\over\displaystyle\nu_0}$. Соответственно, наблюдатель $O$ будет измерять период осциллятора:

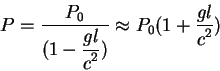
    \begin{displaymath} P={\displaystyle P_0\over\displaystyle(1-{\displaystyle gl\o... ...^2})} \approx P_0(1+ {\displaystyle gl\over\displaystyle c^2}) \end{displaymath}

    Произведение ускорения на расстояние представляет разность гравитационных потенциалов между двумя точками. В первой точке находится лазер, во второй нахаодится наблюдатель: $\phi=gl$. Теперь можно привести формулу определяющую темп течения времени в двух точках $L$ и $O$:
    \begin{displaymath} \tau=t(1 +{\displaystyle\phi\over\displaystyle c^2}) \end{displaymath} (3.1)

    Подставим эту формулу в уравнение для четырехмерного интервала. Поскольку (3.1) представляет связь собственного времени точки $O$, т.е. $\tau$ с координатным временем $t$ (которое мы относим к собственному времени точки $L$, в которой потенциал нулевой), то можно записать четырехмерный интервал как функцию собственного времени и как функцию координатного времени:
    \begin{displaymath} ds^2=c^2 d\tau^2=(1 +{\displaystyle 2\phi\over\displaystyle c^2})\times c^2\; dt^2 \end{displaymath} (3.2)

    Основное изменение по сравнению с прежней величиной, которая характеризовала "расстояние" между событиями в СТО - появление коэффицента перед квадратом дифференциала времени. Этот коэффицент, вообще говоря, является функцией всех четырех координат. Такие функции появляются в том случае, когда метрика является неэвклидовой, а геометрия описывает искривленное пространство - время. Поэтому новая физика - описание сильных гравитационных полей - характеризуется неэвклидовой геометрией. Для работы в общей теории относительности необходимо владеть аппаратом неэвклидовой геометрии, которая будет излагаться позже в этом курсе.

    Вернемся к формуле (3.2). В том случае, когда наблюдатель движется в поле $\phi$ со скоростью $v$, то его собственное время $\tau$ связано с координатным временем $t$ как:
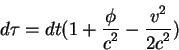    \begin{displaymath} d\tau=dt(1 +{\displaystyle\phi\over\displaystyle c^2} -{\displaystyle v^2\over\displaystyle 2c^2}) \end{displaymath} (3.3)

    Для того, чтобы оценить скорость течения времени в гравитационном потенциале различной величины проведем расчет на сколько "уходят" друг относительно друга часы, находящиеся на полуденной и полуночной стороне Земли в гравитационном поле Солнца. Будем считать, что член пропорциональный квадрату скорости наблюдателей различается для двух наблюдателей на пренебрежимо малую величину. Оценивать разность скорости течения времени будем только по формуле (3.3).
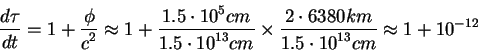    \begin{displaymath} {\displaystyle d\tau\over\displaystyle dt}=1 +{\displaystyle... ...m\over\displaystyle 1.5 \cdot 10^{13} cm}\approx 1 +10^{-12} \end{displaymath} (3.4)

    Это значит, что, скажем, за 12 часов двое часов "разойдутся" на время равное $\sim$ 220 наносекунд. Это вполне обнаружимое, а для некоторых процессов даже большое время. Б$\grave o$льшее время покажут часы, которые расположены дальше от Солнца - часы на полуночной стороне Земли. На рис. 3.1 показан график скорости хода часов в зависимости от расстояния от барицентра Солнца. Вот только для обнаружения этой разницы в скорости течения времени необходимо находиться далеко от Земли, например, на Солнце.

    Тем не менее измерить подобный эффект можно также и на Земле и в ближнем космосе. Рассмотрим два интересных эффекта - изменение скорости хода часов в зависимости от сезона и изменение скорости хода часов установленных на спутнике системы GPS по сравнению с часами установленными на Земле.

    Ось вращения Земли наклонена по отношению к плоскости земной орбиты на угол $\sim 23^{\circ}.5$. Поэтому часы, скажем 1 и 2 с собственным временем $\tau_1$ и $\tau_2$, которые находятся на разных широтах, соответственно $\varphi_1$ и $\varphi_2$, находятся также при разных значениях гравитационного потенциала Солнца. Естественно, что при движении Земли по орбите возникает годовая гармоника в изменении скорости хода часов:

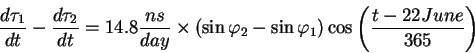
    \begin{displaymath} {\displaystyle d \tau_1\over\displaystyle d t} - {\displayst... ...t( {\displaystyle t - 22 June\over\displaystyle 365} \right) \end{displaymath}

    Здесь в качестве начала отсчета выбран день летнего солнцестояния. На коротких промежутках времени, значительно меньших длительности года такое изменение скорости течения времени воспринимается как линейный дрейф часов, зависящий от широты! Величина этого дрейфа $\sim$ 15 наносекунд в день. Такой эффект действительно наблюдается и природа его никак необъяснима, если "забыть" про эффекты общей теории относительности.

    Общая теория относительности изменила наши взгляды на структуру пространства и времени. В течении долгого времени ОТО оставалась теоретическим инструментом современной физики, который не имеет приложений в технологии. Ситуация существенно измениласьс появлением высокоточной навигации, с появлением спутниковых систем GPS и ГЛОНАСС. Теперь для целей точной навигации (на поверхности Земли) необходимо использовать уравнения общей теории относительности для редукции наблюдений. Особенно важно использовать их для пересчета стандартов времени на Земле и на спутниках. Высота полета спутников превышает земной радиус, а скорость значительно превышает скорость полета современных самолетов. Поэтому изменение скорости течения времени особенно заметны. Собственноре время на борту спутника обозначим $\tau_s$, а на поверхности Земли обозначим $\tau_e$. Отношение двух интервалов составляет:

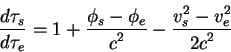
    \begin{displaymath} {\displaystyle d \tau_s\over\displaystyle d \tau_e} = 1 + {\... ...c^2} - {\displaystyle v_s^2 - v_e^2\over\displaystyle 2 c^2} \end{displaymath}

    Здесь индексы $s$ и $e$ соответственно относятся к потенциалу Земли на высоте полета спутника и скорости его полета, а также соответствующие величины для стандарта на Земле.

    Итак, скорость течения времени на Земле и на спутнике различна. Для спутников системы GPS, которые находятся на высоте 14 000 км отличие двух темпов течения времени составляет 44 микросекунды в день. Естественно, для поддержания равномерной шкалы времени, единой для поверхности Земли и спутников необходимо учитывать это изменение.

    5. Неэвклидова геометрия >>

    Разделы

    4. Эксперименты по ОТО

    Насколько все теоретические оценки, которые обсуждались в предыдущих главах соответствуют действительности? Подтверждены ли эти формулы экспериментом? Как мы уже писали, специальная теория относительности используется при расчетах больших машин для физического эксперимента. Использование общей теории относительности задержалось. Ее начали применять в технологии только последние двадцать лет. Использование ее началось с определения скорости течения времени в гравитационном поле с различным потенциалом. Расскажем об экспериментах, которые положили начало применению общей теории относительности в прикладных целях.

    4.1 Эксперименты по проверке скорости хода времени

    Первый эксперимент был сделан в 1971 г.[3]. Четверо часов сделанных на основе цезиевых стандартов частоты были помещены на два самолета и совершили кругосветное путешествие. Одни часы путешествовали в восточном направлении, другие обогнули Землю в западном направлении. Разница в скорости хода времени возникала из-за добавочной скорости вращения Земли. Это был эффект, скорее специальной теории относительности, чем общей, однако, член зависящий от величины земного потенциала в изменении скорости хода часов также присутствовал и внес значимый вклад. Надо сказать, что в первом эксперименте было очень много неопределенностей связанных с неточностью измерения скорости самолетов, высотой самолетов над поверхностью Земли и их положением. Отсутствовал также внешний контроль хода часов и т.п. Тем не менее, удалось подтвердить общую теорию относительности, удалось измерить различие в скорости хода часов на борту двух самолетов. Теоретические вычисления задержки часов были:

    Эффект Восток Запад
    Потенциальный 144 $\pm$ 14 ns 179 $\pm$ 18 ns
    член    
    Допплеровский -184 $\pm$ 18 ns 96 $\pm$ 10 ns
    член    
    Полная -40 $\pm$ 23 ns 275 $\pm$ 21 ns
    задержка    

    Эксперимент дал следущий результат:

      Восток Запад
    Полная -59 ns 273 ns
    задержка    

    Продемонстрируем на простых выкладках, как меняется собственное время часов, которые находятся на борту двух самолетов, один из которых летит на запад, другой на восток. Скорость самолета относительно земной поверхности обозначим $\vec v_a$. Самолет двигается с поверхности вращающейся Земли, его скорость относительно покоющейся системы координат складывается со скоростью вращения Земли $\vec v_E=\vec \Omega \times \vec r$. Выбирая соответсвующие знаки можно это равенство записать также $v_E=\Omega r \cos \varphi$. Здесь $\varphi$ - геоцентрическая широта, которая может быть отождествлена с обычной географической широтой, поскольку сжатие Земли мало $\sim 0.003$ и при наших вычислениях им можно пренебречь.

    В системе координат, которая связана со центром Земли, который находится в состоянии свободного падения в поле тяжести Солнца и планет, время отсчитывается собственными часами $t$. В этой же системе координат скорость самолета есть:

    \begin{displaymath} \vec V_a = \vec v_a + \vec \Omega \times r_a \end{displaymath}

    Разность собственного времени двух часов $\tau_1$ и $\tau_2$ определяется равенством:

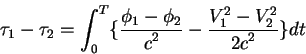
    \begin{displaymath} \tau_1 - \tau_2 = \int_0^T \lbrace{\displaystyle\phi_1 - \ph... ...\displaystyle V_1^2 - V_2^2\over\displaystyle 2c^2}\rbrace d t \end{displaymath}

    Подставляя формулу для скорости самолета относительно центра системы координат получаем, что на борту самолета который летит на восток, скорость течения времени отличается от скорости течения времени на борту самолета, который летит на запад. Эта разность составляет

    \begin{displaymath} 2 v_{ae} \Omega r_a \cos \varphi \end{displaymath}

    Здесь $v_{ae}$ - компонента скорости самолета, направленная на восток. При этом считается, что скорости самолета, который летит на запада и самолета, летящего на восток равны друг другу.

    Отсюда видно, что предсказания общей теории относительности были подтверждены с высокой (для того времени) точностью.

    Измерения временной задержки зависящей от потенциала были сделаны четыре года спустя [4]. Исследователи синхронизовали двое часов, затем поместили одни часы на вершину горы, а вторые оставили на физическом факультете, расположенном у подножья горы. Разница в высоте составляла 3250 м. Время за которое измерялась задержка часов составляло 66 дней. Из - за различия в потенциале гравитационного поля Земли скорости хода часов были различны. Измерения опять подтвердили общую теорию относительности и измерили задержку с точностью $15\%$.

    Два года спустя подобный эксперимент был повторен в Японии [5]. Исследователи поместили одни часы на гору, а другие под гору. Разница высот составляла 2818 м, а время измерения эффекта было две недели. Поскольку часы, используемые японскими исследователями были значительно точнее, точность измерений составляла 5%. Вновь предсказания общей теории относительности были подтверждены.

    Одни из наиболее точных измерений были сделаны во время высотного полета ракеты [6]. На борту ракеты находился водородный мазер, который использовался в качестве высокостабильных часов. Ракета поднялась на 10 000 м, а затем упала в Атлантический океан. Для измерений потенциального члена в задержке часов пришлось компенсировать вклад допплеровского члена (ракета двигалась быстро), а также ионосферные эффекты. Тем не менее измерения были благополучно проведены и правильность формулы для времени задержки была подтверждена с точностью 0.01%.

    Измерения времени задержки проводились также позже на самолетах. В полете осуществлялся постоянный контроль хода часов и стабильности параметров. В частности, был проведен эксперимент по проверке "парадокса близнецов". Были синхронизованы часы, после чего одни часы поместили на борт самолет, а вторые оставили на Земле. Часы, которые находились на борту самолета, по прилету показали, что на борту прошло больше времени, чем на Земле!

    В чем дело? Может быть общая теория относительности неверна? Нет, измерения вновь полностью подтвердили справедливость общей теории относительности, просто надо делать правильные выводы из теоретических положений.

    Классическая формулировка парадокса близнецов относиться к системам координат, которые свободны от неоднородного гравитационного поля. На Земле, разумеется, неоднородное гравитационное поле присутствует. Поэтому надо не только сравнивать задержку времени возникающую на борту самолет из - за движения самолет, но также и задержку времени возникающую из - за потенциального члена. Если самолет движется относительно лаборатории (пробных часов), то часы на его борту будут отставать от часов в лаборатории (это эффект пропорциональный $-{\displaystyle v^2\over\displaystyle 2c^2}$), но самолет летит выше лаборатории, он летит в поле тяжести с ослабленным потенциалом, а значит, часы, находящиеся в лаборатории будут идти медленнее по сравнению с часами, находящимися на борту $+{\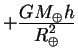displaystyle GM_{\oplus} h\over\displaystyle R^2_{\oplus}}$ (Здесь $h$ -разница высот между самолетом и лабораторией). Сравнить вклад потенциального члена и члена из - за скорости легко. Необходимо сравить величину характерной скорости в данном потенциале (вторая космическая скорость) с реальной скоростью аппарата.

    Для самолет потенциальный член всегда больше. Скорость самолет значительно меньше скорости ракеты, поэтому часы, поднятые на самолете над лабораторией (если они, конечно, подняты на достаточно большую высоту) будут отставать по сравнению с часами, находящимися в лаборатории.

    Теперь формулы для изменения темпа течения времени в зависимости от скорости и высоты используются в навигационной технологии GPS и ГЛОНАСС.

    4.1.1 Парадокс близнецов

    Рассмотрим теперь "парадокс близнецов" в его классической формулировке. Итак, рассматриваются двое часов, одни для простоты будем обозначать $A$, вторые $B$. Часы $A$ все время покоются относительно инерциальной системы координат $K$. Часы $B$ вначале тоже покоются. Часы синхронизируются, затем часы $B$ начинают ускоряться вдоль положительных значений оси $Ox$ системы координат $K$. Через некоторое время ускорение пропадает и часы $B$ по инерции движутся со скоростью $v$ вдоль оси $Ox$ некоторое время. Затем часы вновь ускоряются, но теперь в противоположном направлении, что приводит к их замедлению и полной остановке, а затем к началу движения в противоположном направлении. Часы $B$ ускоряются пока не достигнут скорости $-v$. Затем часы $B$ движутся в направлении к часам $A$. В заранее расчитанный момент времени часы $B$ вновь начинают ускоряться в направлении противоположном движению так, чтобы скорость их уменьшалась. Ускорение вновь подбирается так, чтобы часы $B$ оказались в одной точке с часами $A$ c нулевой скоростью. После этого показания часов сравниваются. Ускорения в этом мысленном эксперименте можно сделать достаточно большими, так что влияние участков движения с ненулевым ускорением на процесс вычисления задержки часов можно считать пренебрежимо малым. Тогда часы $B$ должны отстать от часов $A$ на некоторый интервал времени. Итак, для наблюдателя, сопутствующего часам $A$ движущиеся часы должны отстать.

    Рассмотрим этот же процесс с точки зрения наблюдателя сопутствующего часам $B$. Он имеет противоположные характеристики, так что с его точки зрения "отстать" должны часы $A$. Ниже мы проанализируем правильный ход рассуждений и покажем, что на самом деле для обеих наблюдателей часы $B$ должны отстать по сравнению с часами $A$. Причиной неправильных рассуждений является наличие поля ускорения в системе координат сопутствующей часам $B$. Поэтому изменения интервалов времени в системе сопутствующей $B$ надо считать уже по формулам общей теории относительности, а не только по формулам специальной теории относительности.

    Одно из лучших изложений "парадакса близнецов" привел А.Эйнштейн в своей популярной статье "Диалог по поводу возражений против теории относительности" приведенной в книге [7]. Будем следовать этому изложению, подкрепляя его расчетами. Весь процесс путешествия и возвращения часов можно разделить на пять стадий.

    С точки зрения $A$      С точки зрения $B$
    1. Часы $B$ ускоряются внешними силами в направлении положительных значений оси $Ox$, пока не приобретут скорость $v$. Часы $A$ покоются.      1. В отрицательном направлении оси $Ox$ возникает гравитационное поле, в котором $A$ падает ускоренно. Часы $B$ удерживаются внешними силами в покое. Когда $A$ приобретают скорость $v$ гравитационное поле исчезает.
    2. Часы $B$ движутся с постоянной скоростью до точки 2. Часы $A$ покоятся.      2. Часы $A$ движутся с постоянной скоростью до точки $\hat 2$. Часы $B$ покоятся.
    3. Часы $B$ ускоряются внешними силами пока не приобретут скорость $-v$.      3. Появляется однородное поле тяжести направленое в сторону положительных значений оси $Ox$, под действием которого $A$ ускоряются в положительном направлении до тех пор пока не приобретут скорость $+v$. После этого поле исчезает. Внешние силы удерживают часы $B$.
    4. Часы $B$ движутся назад с постоянной скоростью $v$, пока не приблизятся к $A$. Часы $A$ покоятся.      4. Часы $A$ движутся со скоростью $v$ в направлении положительных значений оси $Ox$, до тех пор, пока не приблизятся к $B$. Часы $B$ остаются в покое.
    5. Часы $B$ останавливаются внешними силами.      5. Возникает поле тяжести, которое останавливает часы $A$. Часы $B$ удерживаются внешними силами.

    Как видим, две системы координат неэквивалентны друг другу. С точки зрения наблюдателя сопутсвующего часам $A$ гравитационное поле отсутствует, с точки зрения наблюдателя сопутствующего часам $B$ гравитационное поле не равно нулю. Для вычисления скорости хода часов с точки зрения наблюдателя $A$ достаточно формул, выведенных в рамках СТО, с точки зрения наблюдателя $B$ при вычислении скорости хода времени необходимо учитывать эффекты ОТО.

    Вновь аккуратно учитывая разницу между системами координат вычислим скорость хода часов в системе $K$ и в системе $\hat K$ и сравним какие из часов отстануть от других.

    Расчет будем вести применяя приближенные формулы СТО и ОТО для того, чтобы расчеты были легче и не затемнялся смысл формул, мы будем считать, что скорость $v$ значительно меньше чем скорость света.

    Вначале рассчитаем задержку времени по формулам СТО с точки зрения наблюдателя сопутствующего часам $A$. Будем считать, что время ускорения пренебрежимо мало. Тогда разность скорости хода часов во время первой стадии, а также во время третьей и пятой стадии ппренебрежимо мало. Тогда интервал времени показанный часами в течении всего путешествия $B$ зависит от интервала времени показанному часами $A$ как:

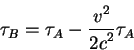
    \begin{displaymath} \tau_B=\tau_A - {\displaystyle v^2\over\displaystyle 2c^2}\tau_A \end{displaymath}

    Здесь $\tau_A$ - полное время путешествия туда - обратно.

    Итак с точки зрения наблюдателя сопутствующего часам $A$ часы $B$ отстают.

    Проведем расчет скорости хода обеих часов с точки зрения наблюдателя сопутствующего часам $B$. Во время первой стадии разность хода пренебрежимо мала. Оба чдена дают пренебрежимо малый вклад. Потенциальный - потому что часы $A$ и $B$ находятся практически только в одной точке, а вклад от потенциального члена пропорционален разности расстояний, член зависящий от скорости тоже мал.

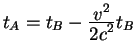    Во время второй стадии движения по инерции, которая длится время, скажем, $t_B$ часы $A$ отстают от часов $B$ как $t_A=t_B -{\displaystyle v^2\over\displaystyle 2c^2}t_B$.

    Будем считать, что третья стадия длится интервал времени $t_r$. Во время третьей стадии вклад члена пропорционального скорости часов в разность хода часов пренебрежимо мал. Однако велик вклад потенциального члена. Действительно за время $t_B$ часы $A$ прошли относительно часов $B$ расстояние $L=vt_B$. Ускорение, требуемое для изменения скорости с $+v$ на $-v$ в течении времени $t_r$ составляет $g={\displaystyle 2v\over\displaystyle t_r}$.

    Гравитационный потенциал между точками нахождения двух часов составляет величину $\phi= +gL$. Знак плюс выбран потому, что ускорение направлено от $A$ к $B$. После окончания третьей стадии из - за потенциального члена интервал времени $T_A$ показанный часами $A$ и интервал времени $T_B$ показанный часами $B$ связаны равенством

    \begin{displaymath} T_A=T_B +\frac{gL}{c^2} t_r \end{displaymath}

    Обратим внимание, что второе слагаемое в этой формуле имеет положительный знак. Это означает, что часы $A$ теперь идут быстрее, чем часы $B$.

    В течении четвертой стадии часы $A$ вновь отстают от часов $B$. Обратный путь длится тот же интервал времени $\hat t_B=t_B$. За этот интервал часы $A$ вновь отстают. Интервал времени, который показывают часы $A$ составляет:

    \begin{displaymath} \hat t_A=\hat t_B -\frac{v^2}{2c^2}\hat t_B \end{displaymath}

    В течении пятой стадии часы $A$ вновь замедляются гравитационным полем. Однако теперь разность хода часов $A$ и $B$ опять пренебрежимо мала, по тем же причинам, что и на первой стадии.

    Посчитаем полный интервал времени, который показывают часы $A$ с точки зрения наблюдателя, сопутствующего часам $B$. Промежуток времени, который показывают часы $A$ складывается из промежутков времени показываемых этими часами с первой по пятую стадии:

    \begin{displaymath} \hat \tau_A=t_A +T_A +\hat t_A \end{displaymath}

    Поэтому полный интервал времени показанный часами $A$ с точки зрения наблюдателя сопутствующего часам $B$ есть:

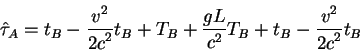
    \begin{displaymath} \hat \tau_A=t_B -{\displaystyle v^2\over\displaystyle 2c^2}t... ...c^2} T_B + t_B -{\displaystyle v^2\over\displaystyle 2c^2}t_B \end{displaymath}

    Подставим значение полного врмени путеществия туда - обратно $\tau_B=2t_B$. Кроме того, подставим значения $g={\displaystyle 2v\over\displaystyle T_B}$ и $L=vt_B$, выражая полное равенство только через $v$. Окончательно получаем, что

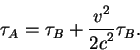
    \begin{displaymath}\tau_A=\tau_B +{\displaystyle v^2\over\displaystyle 2c^2}\tau_B.\end{displaymath}

    Теперь видно, что интервал времени показываемый часами $A$ оказывается больше, чем интервал времени показываемый часами $B$. Это значит, что путешествующие часы покажут меньший промежуток времени, чем часы покоящиеся относительно инерциальной системы координат. Этот расчет демонстрирует отсутствие "парадокса близнецов" в релятивистской физике.

    6. Анализ в неэвклидовой >>

    Разделы

    5. Неэвклидова геометрия

    В классической физике пространство было эвклидовым, а время абсолютным и единым для всего пространства. В релятивистской физике, как мы уже убедились из материала предыдущей главы пространство является неэвклидовым. В общем случае геометрия представляет из себя четырехмерное дифференцируемое многообразие,

    В произвольной геометрии рассматриваются произвольные преобразования координат:

    \begin{displaymath} x^{\mu} = f^{\mu}(\tilde x^{\nu}), \end{displaymath}

    например,

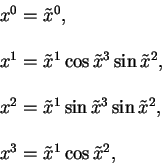
    \begin{displaymath} \begin{array}{l} x^0 = \tilde x^0, \\ \qquad \\ x^1 = \til... ...2, \\ \qquad \\ x^3 = \tilde x^1 \cos \tilde x^2, \end{array}\end{displaymath}

    как видно из приведенных преобразований, они описывают просто переход от сферических к декартовым координатам.

    Дифференциал в нетильдованной системе связан с дифференциалом в системе координат с тильдой уравнениями вида:

    \begin{displaymath} d x^{\mu} = {\displaystyle\partial f^{\mu}\over\displaystyle... ...mu}\over\displaystyle\partial \tilde x^{\nu}} d\tilde x^{\nu} \end{displaymath}

    В геометрии вводится понятие геометрического объекта. Не перечисляя всех объектов геометрии назовем только скаляры, векторы и тензоры. Строго говоря, все перечисленные величины являются тензорами, так скаляр является тензором нулевого ранга, а вектор тензором первого ранга. Однако исторически принято выделять скаляры и векторы.

    Скалярная величина (или скаляр) при преобразованиях системы координат не преобразуется,

    \begin{displaymath} \varphi(x^{\mu}) = \varphi(\tilde x^{\mu}) \end{displaymath}

    Вектором называется величина, которая содержит четыре компоненты, преобразуемые согласно правилу:
    \begin{displaymath} A^{\mu} = {\displaystyle\partial x^{\mu}\over\displaystyle\partial \tilde x^{\nu}} \tilde A^{\nu} \end{displaymath} (5.1)

    для контравариантных компонент и
    \begin{displaymath} A_{\mu} = {\displaystyle\partial \tilde x^{\nu}\over\displaystyle\partial x^{\mu}} \tilde A_{\nu} \end{displaymath} (5.2)

    для ковариантных компонент.

    Как можно заметить, из закона преобразования (5.1) преобразование контравариантных компонент какого - либо вектора подобно преобразованию дифференциалов координат, представляющих разность положений двух точек. Следовательно контравариантные компоненты вектора можно представить как систему из двух точек, с указанием какая из точек является первой, а какая является второй. Примером контравариантных компонент является четырехмерная скорость какого - либо тела.

    Примером ковариантных компонет вектора является градиент некоторого поля:

    \begin{displaymath} A_{\mu} = {\displaystyle\partial \varphi(x^{\alpha})\over\displaystyle\partial x^{\mu}} \end{displaymath}

    Образом градиента от поля являются наборы двумерных поверхностей определяющих постоянство поля $\varphi(x^{\alpha})$. Следовательно геометрическим образом ковариантных компонент тензора являются двумерные поверхности "раскрашенные" в различные "цвета" для того, чтобы определить какая из поверхностей является первой, а какая - второй.

    Выпишем также правило по которому преобразуются компоненты тензора второго ранга:

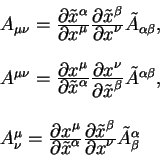
    \begin{displaymath} \begin{array}{l} A_{\mu \nu} = {\displaystyle\partial \tilde... ...aystyle\partial x^{\nu}} \tilde A^{\alpha}_{\beta} \end{array}\end{displaymath}

    Геометрическая величина $A^{\mu_1 \mu_2 ... \mu_n}_{\nu_1 \nu_2 ... \nu_m}$, которая имеет $n$ верхних ипндексов и $m$ нижних индексов и преобразуется по закону:

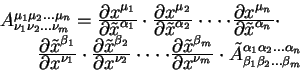
    \begin{displaymath} \begin{array}{l} A^{\mu_1 \mu_2 ... \mu_n}_{\nu_1 \nu_2 ... ... ...ha_2 ... \alpha_n}_{\beta_1 \beta_2 ... \beta_m} \end{array} \end{displaymath}

    называется тензором ранга $n+m$ с $n$ контравариантными $m$ ковариантными индексами.

    В алгебре тензоров определяется суммирование тензоров одинакового ранга и с одинаково расположенными индексами:

    \begin{displaymath} C^{\mu}_{\nu} = A^{\mu}_{\nu} + B^{\mu}_{\nu}, \end{displaymath}

    умножение определено для тензоров любого ранга с произвольно расположенными индексами:

    \begin{displaymath} C^{\mu \alpha \beta}_{\nu} =A^{\mu}_{\nu} \cdot B^{\alpha \beta} \end{displaymath}

    В тензорной алгебре определяют также свертку двух тензоров по правилу:

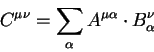
    \begin{displaymath} C^{\mu \nu} = \sum_{\alpha} A^{\mu \alpha} \cdot B^{\nu}_{\alpha} \end{displaymath}

    для произвольного расположения индексов важно только, чтобы индекс по которому проводится свертка в первом тензоре был верхним, во втором - нижним (или наоборот, в первом - нижним, а во втором -верхним). Положение и количество остальных индексов переносится в свертку по их месту. Свертки могут быть образованы различными способами, однако каждое суммирование должно выполняться по верхнему и нижнему индексу. Например, сумма

    \begin{displaymath} \sum_{\alpha} A^{\mu}_{\alpha} \cdot B^{\nu}_{\alpha} \end{displaymath}

    не является тензором, как легко убедиться рассмотрев закон преобразования этой величины.

    В современной тензорной алгебре, анализе и физике пользуются правилом суммирования Эйнштейна, который для удобства ввел следущее обозначение:

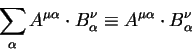
    \begin{displaymath} \sum_{\alpha} A^{\mu \alpha} \cdot B^{\nu}_{\alpha} \equiv A^{\mu \alpha} \cdot B^{\nu}_{\alpha} \end{displaymath}

    при этом индекс $\alpha$ называют мертвым индексом и по повторяющимся индексам производится суммирование. Так запись $C_{\mu \nu}A^{\mu}B^{\nu}$ обозначает:

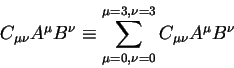
    \begin{displaymath} C_{\mu \nu}A^{\mu}B^{\nu} \equiv \sum_{\mu=0, \nu=0}^{\mu=3, \nu=3} C_{\mu \nu}A^{\mu}B^{\nu} \end{displaymath}

    Повсюду в этой книге мы будем использовать это правило, два повторяющихся индекса один верхний, другой - нижний будет означать, что по ним производится суммирование.

    Определим также обратные тензоры согласно уравнению:

    \begin{displaymath} A_{\mu \alpha} \cdot B^{\nu \alpha} = \delta^{\mu}_{\nu} \end{displaymath}

    Здесь $\delta^{\mu}_{\nu}$ - символ Кронекера, который определяется следущими условиями $\delta^{\mu}_{\nu} =1$ если $\mu = \nu$ и $\delta^{\mu}_{\nu}=0$ если $\mu \ne \nu$. Можнл также выписать матрицу символа Кронекера
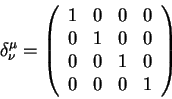    \begin{displaymath} \delta^{\mu}_{\nu} =\left( \begin{array}{rrrr} 1 & 0 & 0 & 0... ...& 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array}\right) \end{displaymath} (5.3)

    Свертка двух тензоров понижает ранг произведения. Так, важный пример показывает, что произведение ковариантных компонент вектора на контравариантные компоненты является инвариантом:
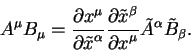    \begin{displaymath} A^{\mu} B_{\mu} = {\displaystyle\partial x^{\mu}\over\displa... ...laystyle\partial x^{\mu}} \tilde A^{\alpha} \tilde B_{\beta}. \end{displaymath} (5.4)

    Различные авторы [8], [9], [12] вводят также операцию симметрирования, албтернирования, выключения индексов и т.п. Для нас важной остается только последняя операция над тензорами - образование следа, образование поперечной части тензора и образование поперечно - бесследовой части тензора, которые будут применяться во второй части книги. Однако для их определения нам придется использовать метрику, поэтому отложим введения этих понятий после обсуждения метрики.

    5.1 Метрика искривленного пространства - времени

    Геометрия четырехмерного пространства - времени полностью определяется десятью функциями, которые являются компонентами симметричного тензора второго ранга. Метрика четырехмерного интервала есть:


    \begin{displaymath} d s^2 = g_{\mu \nu} d x^{\mu} d x^{\nu} \end{displaymath} (5.5)

    Здесь $g_{\mu \nu}$ - ковариантные компоненты метрического тензора или, как обычно говорят, метрический тензор второго ранга.

    Компоненты метрического тензора являются, вообще говоря, функциями всех четырех координат.

    Преобразованием координат всегда можно добиться того, чтобы компоненты метрического тензора были приведены к виду метрики Минковского:
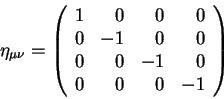    \begin{displaymath} \eta_{\mu \nu} =\left( \begin{array}{rrrr} 1 & 0 & 0 & 0 ... ...0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \\ \end{array}\right) \end{displaymath} (5.6)

    В пространстве с заданной метрикой можно определить связь между ковариантными и контравариантными компонентами тензоров, так для вектора связь между этими компонентами задается уравнениями:

    \begin{displaymath} A_{\mu} = g_{\mu \alpha} A^{\alpha} \end{displaymath}

    Теперь можно определить норму вектора, аналогично тому, как это делается в эвклидовой геометрии. Норомой вектора по определению полагают величину [8], [9], [12]:
    \begin{displaymath} \vert\vert A \vert\vert^2 = A_{\mu} A^{\mu} = g_{\mu \nu} A^{\mu} A^{\nu} \end{displaymath} (5.7)

    В зависимости от того, чему равна норма ветора его называют:

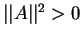
    • времениподобным, если $\vert\vert A \vert\vert^2 >0$         
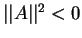
    • пространственноподобным, если $\vert\vert A \vert\vert^2 <0$         
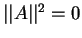
    • изотропным, если $\vert\vert A \vert\vert^2 = 0$

    Норма называется также длиной вектора. Как видно из определения изотропного вектора он обладает нулевой длиной.

    Рассмотрим свертку двух векторов. Два вектора, которые удовлетворяют условию:

    \begin{displaymath} A_{\mu} B^{\mu} = g_{\mu \nu} A^{\mu} B^{\nu} = 0 \end{displaymath}

    называются ортогональными. Отсюда можно сделать вывод, что изотропный вектор ортогонален самому себе и любому другому изотропному вектору. Следует заметить, что таким свойством обладают только изотропные вектора.

    Кроме этого важного свойства приведем также уравнение описывающее угол $\varphi$ между двумя векторами $A^{\mu}$ и $B^{\nu}$ в неэвклидовой геометрии:
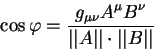    \begin{displaymath} \cos \varphi = {\displaystyle g_{\mu \nu} A^{\mu} B^{\nu}\ov... ...isplaystyle\vert\vert A\vert\vert\cdot \vert\vert B\vert\vert} \end{displaymath} (5.8)

    Здесь следует заметить, что оба вектора $A$ и $B$ являются либо пространственноподобными, либо изотропными.

    5.1.1 Примеры метрики искривленного пространства

    Приведем примеры метрики искривленного пространства. На самом деле в быту мы сталкиваемся с примера геометрии искривленного пространства значительно чаще, чем привыкли думать. Поверхность мяча, поверхность спинки кресла, поверхность кувшина или графина - вот неполный список двумерных искривленных пространств. Примеры идеальных плоскостей, таких как крышка стола или ровный листок бумаги в этом ряду выглядят, скорее исключениями, чем правилом.

    Приведем в качестве примера метрику на поверхности сферы. Для этого выпишем вначале метрику эвклидова пространства в сферической системе координат:

    \begin{displaymath} dl^2=dr^2 + r^2 \left(d\theta^2 + \sin^2 \theta d\varphi^2\right) \end{displaymath}

    Будем считать, что мы вычисляем расстояние только между теми точками, которые лежат на поверхности сферы радиуса $R$. Тогда можно полагать, что $d R =0$, а значит метрика получает вид:
    \begin{displaymath} dl^2= R^2 \left(d\theta^2 + \sin^2 \theta d\varphi^2\right) \end{displaymath} (5.9)

    теперь метрика описывает поверхность сферы, а геометрия, которую описывает данный метрический тензор является неэвклидовой.

    5.2 Геодезические линии в неэвклидовой геометрии

    В эвклидовой геометрии очень важным понятием является прямая между двумя точками, которая к тому же является кратчайшим расстоянием между этими точками. В неэвклидовой геометрии понятие прямой заменяется понятием геодезической линии, которая является экстремальным путем между двумя точками.

    Для нахождения уравнения геодезической линиии применим вариационное исчисление.

    Длина линии в геометрии общей теории относительности есть интеграл по интервалу между двумя событиями разделенными по времени и пространству:

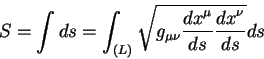
    \begin{displaymath} S = \int d s = \int_{(L)} \sqrt{g_{\mu \nu} {\displaystyle d... ...le d s} {\displaystyle d x^{\nu}\over\displaystyle d s}} d s \end{displaymath}

    Линии экстремального пути удовлетворяет условию:

    \begin{displaymath} \delta S = \int \delta d s= 0 \end{displaymath}

    Здесь символ $\delta$ означает первую вариацию. Из этого условия получается уравнение геодезической линии.

    Для вычисления вариации величины $S$ применим следущий прием. Проварьируем не дифференциал интервала $d s$, а квадрат дифференциала $ds^2$. Вариации самого дифференциала по вариациям квадрата можно получить согласно уравнению $\delta ds^2 = 2ds \delta ds$. С другой стороны, вариации квадрата $ds^2$ есть:

    \begin{displaymath} \delta ds^2 = \delta \left( g_{\mu \nu} d x^{\mu} d x^{\nu}\right) \end{displaymath}

    правую часть этого равенства можно представить в виде суммы:

    \begin{displaymath} \delta ds^2 = \delta g_{\mu \nu} d x^{\mu} d x^{\nu} + g_{\m... ...d x^{\mu} d x^{\nu} + g_{\mu \nu} d x^{\mu} \delta d x^{\nu} \end{displaymath}

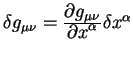    Воспользуемся равенствами $\delta d x^{\mu} =d \delta x^{\mu}$ и $\delta g_{\mu \nu} = {\displaystyle\partial g_{\mu \nu}\over\displaystyle\partial x^{\alpha}} \delta x^{\alpha}$ и получим уравнение для вариации дифференциала интервала:

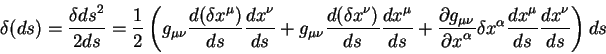
    \begin{displaymath} \delta(ds) = {\displaystyle\delta ds^2\over\displaystyle 2ds... ...} {\displaystyle d x^{\nu}\over\displaystyle d s} \right) ds \end{displaymath}

    Третий член в круглых скобках уже приведен к виду пригодному для вычисления первой вариации. Для приведения к такому же виду первых двух членов воспользуемся равенством:

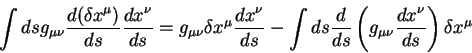
    \begin{displaymath} \int ds g_{\mu \nu} {\displaystyle d(\delta x^{\mu})\over\di... ...tyle d x^{\nu}\over\displaystyle d s} \right) \delta x^{\mu} \end{displaymath}

    Воспользуемся теперь этими равенствами и вычислим первую вариацию полного пути:

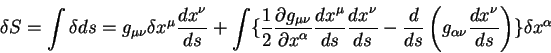
    \begin{displaymath} \delta S = \int \delta ds = g_{\mu \nu} \delta x^{\mu} {\di... ...{\nu}\over\displaystyle d s} \right) \rbrace \delta x^{\alpha} \end{displaymath}

    В этом уравнении первый член после второго знака равенства представляет из себя вариации в конечных точках пути, по определению эти вариации равны нулю [13], [14]. Член под знаком интеграла в фигурных скобках должен обращаться в нуль на геодезической линии. Это и дает нам уравнение геодезической линии:
    \begin{displaymath} {\displaystyle d u_{\alpha}\over\displaystyle d s} = \frac{1... ...mu \nu}\over\displaystyle\partial x^{\alpha}} u^{\mu} u^{\nu} \end{displaymath} (5.10)

    Здесь $u^{\mu}$ - вектор касательный к геодезической линии.

    Уравнение, которое мы получили является уравнением второго порядка. В случае эвклидовой геометрии, когда все компоненты метрического тензора являются диагональными и равны единице, правая часть равенства (5.10) равна нулю. Тогда решение этого уравнения есть $u_{\alpha} = const$. Это решение описывает прямые линии, которые являются линиями кратчайшего пути в эвклидовой геометрии.

    Приведем это уравнение к стандартной форме, принятой в неэвклидовой геометрии. Для этого воспользуемся тождеством:

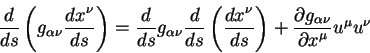
    \begin{displaymath} {\displaystyle d\over\displaystyle d s}\left( g_{\alpha \nu}... ...\alpha \nu}\over\displaystyle\partial x^{\mu}} u^{\mu} u^{\nu} \end{displaymath}

    Подставив его в левую часть уравнения (5.10) получаем уравнение вида:

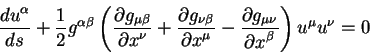
    \begin{displaymath} {\displaystyle d u^{\alpha}\over\displaystyle d s} + \frac{1... ...ver\displaystyle\partial x^{\beta}}\right) u^{\mu} u^{\nu} = 0 \end{displaymath}

    Величина
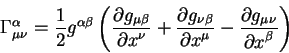    \begin{displaymath} \Gamma^{\alpha}_{\mu \nu} = \frac{1}{2} g^{\alpha \beta}\lef... ...artial g_{\mu \nu}\over\displaystyle\partial x^{\beta}}\right) \end{displaymath} (5.11)

    называется символом Кристоффеля. Символ Кристоффеля имеет три индекса и не является тензором. В алгебре такие величины носят название символы первого рода.

    Стандартный вид уравнения геодезической линии в неэвклидовой геометрии записывается с помощью символа Кристоффеля:
    \begin{displaymath} {\displaystyle d u^{\alpha}\over\displaystyle d s} + \Gamma^{\alpha}_{\mu \nu} u^{\mu} u^{\nu} = 0 \end{displaymath} (5.12)

    Кроме этого, стандартного вида уравнения геодезической линии, можно также записать как меняется дифференциал касательного вектора $u^{\mu}$ при переносе вдоль геодезической линии:
    \begin{displaymath} d u^{\alpha} =- \Gamma^{\alpha}_{\mu \nu} u^{\mu} d x^{\nu} \end{displaymath} (5.13)

    5.2.1 Геодезические линии на поверхности сферы

    Рассмотрим в качестве примера геодезические линии на сфере - двумерной неэвклидовой поверхности. Метрический тензор на поверхности сферы имеет вид:
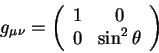    \begin{displaymath} g_{\mu \nu} =\left( \begin{array}{cc} 1 & 0 \\ 0 & \sin^2 \theta \\ \end{array}\right) \end{displaymath} (5.14)

    Контравариантные компоненты метрического тензора на поверхности сферы есть:
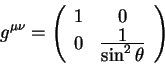    \begin{displaymath} g^{\mu \nu} =\left( \begin{array}{cc} 1 & 0 \\ 0 & {\displaystyle 1\over\displaystyle\sin^2 \theta} \\ \end{array}\right) \end{displaymath} (5.15)

    Вычисляя символ Кристоффеля получаем, что все компоненты равны нулю за исключением двух:

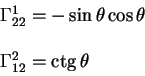
    \begin{displaymath} \begin{array}{l} \Gamma^1_{22} = - \sin \theta \cos \theta \\ \qquad \\ \Gamma^2_{12} = \ctg \theta \end{array}\end{displaymath}

    Уравнения геодезических линий имеют вид:
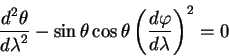    \begin{displaymath} {\displaystyle d^2 \theta\over\displaystyle d\lambda^2} - \s... ...playstyle d \varphi\over\displaystyle d \lambda} \right)^2 =0 \end{displaymath} (5.16)

    и


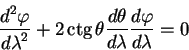    \begin{displaymath} {\displaystyle d^2 \varphi\over\displaystyle d\lambda^2} + 2... ...bda} {\displaystyle d \varphi\over\displaystyle d \lambda} =0 \end{displaymath} (5.17)

    Здесь $\theta$, $\varphi$ сферические координаты наклонения и азимута, а $\lambda$ - афинный параметр вдоль геодезической линии.

    При приведении к первому интегралу уравнение (5.17) получает вид:

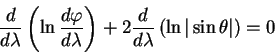
    \begin{displaymath} {\displaystyle d\over\displaystyle d \lambda}\left( \ln {\di... ...aystyle d \lambda}\left( \ln \vert\sin \theta\vert \right) = 0 \end{displaymath}

    или


    \begin{displaymath} \sin^2 \theta {\displaystyle d \varphi\over\displaystyle d \... ...ta_0 {\displaystyle d \varphi\over\displaystyle d \lambda}_0 \end{displaymath} (5.18)

    Здесь 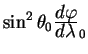$\sin^2 \theta_0 {\displaystyle d \varphi\over\displaystyle d \lambda}_0$ обозначает константу интегрирования. Первый интеграл уравнения (5.16) можно легко привести к удобной форме, если выбрать в качестве афинного параметра длину вдоль геодезической $d s = d \lambda$. Тогда интеграл первого уравнения становится:
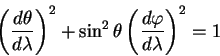    \begin{displaymath} \left( {\displaystyle d \theta\over\displaystyle d \lambda} ... ...splaystyle d \varphi\over\displaystyle d \lambda} \right)^2 =1 \end{displaymath} (5.19)

    Рассмотрим два частных случая геодезических линий.

    Движение по экватору

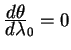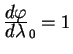    Пусть наша линия начинается на экваторе $\theta_0 = {\displaystyle\pi\over\displaystyle 2}$, причем направление этой линии совпадает с направлением экватора, т.е. ${\displaystyle d \theta\over\displaystyle d \lambda} _0=0$ и ${\displaystyle d \varphi\over\displaystyle d \lambda} _0=1$.

    Решение для геодезической линии получается из уравнений (5.18, 5.19). Действительно, правая часть равенства (5.18) есть 1. Подставляем выражение для ${\displaystyle d \varphi\over\displaystyle d \lambda}$ в уравнение (5.19) и получаем уравнение:

    \begin{displaymath} ({\displaystyle d \theta\over\displaystyle d \lambda})^2 = - \ctg^2 \theta \end{displaymath}

    Удовлетворяет этому уравнению только значения $\theta= {\displaystyle\pi\over\displaystyle 2}$. Таким образом доказано, что экватор является геодезической линией на сфере.

    Движение по меридиану

    Рассмотрим теперь движение вдоль меридиана и покажем, что меридиан также является геодезической линией. Теперь вектор, касательный к линии имеет компоненты:

    \begin{displaymath} {\displaystyle d \varphi\over\displaystyle d \lambda} _0=0 \... ...m} {\displaystyle d \theta\over\displaystyle d \lambda} _0=1 \end{displaymath}

    Начальную точку также выберем на экваторе $\theta_0 = {\displaystyle\pi\over\displaystyle 2}$. Из уравнения (5.18) получаем, что

    \begin{displaymath} {\displaystyle d \varphi\over\displaystyle d \lambda} = 0 \end{displaymath}

    откуда следует, что $\varphi(\lambda) = const$. Из второго интеграла системы (5.19) получаем, что

    \begin{displaymath} {\displaystyle d \theta\over\displaystyle d \lambda} = \pm 1 \end{displaymath}

    откуда непосредственно следует, что

    \begin{displaymath} \theta (\lambda) =\pm \lambda + {\displaystyle\pi\over\displaystyle 2} \end{displaymath}

    Не рассматривая общего случая решения системы (5.18, 5.19) упомянем только, что экватор и меридиан на поверхности сферы являются частными случаями большого круга - сечения поверхности сферы плоскостью, которая проходит через центр сферы. Рассматривая трехмерные вращения, можно показать, что только отрезок большого круга на сфере представляет кусок геодезической линии. Полная геодезическая линия представляет из себя большой круг.

    Движение по малому кругу

    Продемонстрируем отличие произвольной линии от геодезической линии на примере малого круга на сфере. Малый круг на сфере - это сечение сферы плоскостью, которая не проходит через центр сферы.

    Выберем малый круг так, чтобы он был сечением с $\theta = const$. Тогда уравнения, которые описывают малый круг есть:

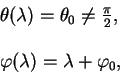
    \begin{displaymath} \begin{array}{l} \theta(\lambda) = \theta_0 \ne {\pi \over 2... ...qquad \\ \varphi( \lambda) = \lambda + \varphi_0 , \end{array}\end{displaymath}

    отсюда легко найти первые и вторые производные от координат по афинному параметру:

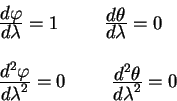
    \begin{displaymath} \begin{array}{l} {\displaystyle d \varphi\over\displaystyle ... ...yle d^2 \theta\over\displaystyle d \lambda^2} = 0 \end{array}\end{displaymath}

    Подставляя эти значения в уравнения геодезических приходим к противоречию:

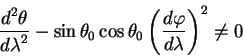
    \begin{displaymath} {\displaystyle d^2 \theta\over\displaystyle d \lambda^2} -\s... ...aystyle d \varphi\over\displaystyle d \lambda}\right)^2 \ne 0 \end{displaymath}

    Таким образом малый круг на сфере не является геодезической линией.

    7. Тензор кривизны >>

    Разделы

    6. Анализ в неэвклидовой геометрии

    Вычисление различных величин в общей теории относительности - это вычисление тензорных величин различного ранга (скалярных, векторных, тензорных второго ранга, иногда более высоких рангов), включая операции дифференцирования и интегрирования. В эвклидовой геометрии операция дифференцирования для, например, векторов, определялась так же как для обычных математических функций - скалярных величин. В неэвклидовой геометрии процедура построения производных от вектора является более сложной. Она носит название ковариантного дифференцирования.

    6.1 Ковариантное дифференцирование

    Напомним, что если в каждой точке некоторой области (которое может охватывать и все пространство) задана некоторая скалярная или векторная величина, то говорят, что задано поле этой величины. Аналогично можно задать поле тензорной величины. Скажем метрика Минковского, определяемая как (5.6), является тензорным полем второго ранга, определенным во всех пространстве. Каждая компонента этого поля является постоянной величиной, причем диагональные компоненты отличны от нуля ($g_{00}=1$, $g_{11}=g_{22}=g_{33}=-1$), а недиагональные равны нулю. Примером тензорного поля второго ранга, которое не является постоянным может служить метрика на поверхности сферы. Недиагональные компоненты такой метрики, как и в предыдущем примере, равны нулю, но из диагональных компонент только компонента $g_{11}=1$, тогда как вторая компонента является функцией одной из координат $g_{22}=\sin^2 \theta$.

    В пространстве с эвклидовой или псевдоэвклидовой метрикой в векторном и тензорном анализе можно определить производные от соответствующего поля по стандартным правилам:
    \begin{displaymath} \frac{\partial A_{\alpha}}{\partial x^{\mu}}= \lim_{\Delta x... ...htarrow 0} \frac{\Delta A_{\alpha}(x^{\mu})}{\Delta x^{\mu}} \end{displaymath} (6.1)

    при $\Delta x^{\mu} \rightarrow 0$. Здесь необходимо обратить внимание на то, что в правой части стоит дробь, в числителе которой находится разность тензорных величин, взятых в двух соседних точках, $\Delta A_{\alpha} (x^{\mu})=A_{\alpha}(x^{\mu} +\Delta x^{\mu}) -A_{\alpha}(x^{\mu})$.

    В пространстве с эвклидовой метрикой разность двух векторов, даже взятых в различных точках пространства является вектором. Эта разность при линейных преобразованиях координат преобразуется как вектор.

    При нелинейных преобразованиях координат или в пространстве с неэвклидовой метрикой разность двух векторов, взятых в различных точках пространства преобразуется уже не по закону преобразования векторов. Хотя подробное изложение правил тензорного анализа можно найти в прекрасных учебниках [8], [9], [10], мы посвятим несколько абзацев демонстрации особенностей нелинейных преобразований и преобразований в неэвклидовых пространствах.

    Вначале покажем, что при нелинейных преобразованиях дифференциал векторного поля уже не является векторным полем.

    Итак, введем стандартное обозначение:

    \begin{displaymath} \Delta A_{\mu}= A_{\mu}(x^{\alpha} +\Delta x^{\alpha}) - A_{\mu}(x^{\alpha}) \end{displaymath}

    и сделаем преобразование координат $\hat x^{\mu}=f^{\mu}(x^{\nu})$, законы преобразования для векторного поля есть


    \begin{displaymath} A_{\mu}(x^{\alpha})=\frac{\partial \hat x^{\nu}}{\partial x^{\mu}}\hat A_{\nu}\left(\hat x^{\beta}(x^{\alpha})\right) \end{displaymath}

    Поле $A_{\nu}$ в точке $x^{\alpha} +\Delta x^{\alpha}$ будет преобразовываться согласно

    \begin{displaymath} A_{\mu}(x^{\alpha} +\Delta x^{\alpha})=\frac{\partial \hat ... ...u}\left(\hat x^{\beta}(x^{\alpha} +\Delta x^{\alpha})\right) \end{displaymath}

    Дифференциал вычисляется в точке $x^{\alpha}$, поэтому все функции необходимо вычислить именно в этой точке. Для вычисления частной производной в точке $x^{\alpha}$ используем вычисления вряд Тэйлора по малому параметру - величине дифференциала $\Delta x^{\alpha}$:

    \begin{displaymath} \frac{\partial \hat x^{\nu}(x^{\alpha} +\Delta x^{\alpha})}{... ...ystyle\partial x^{\mu} \partial x^{\gamma}} \Delta x^{\gamma} \end{displaymath}

    аналогичные вычисления проделаем для самого векторного поля:

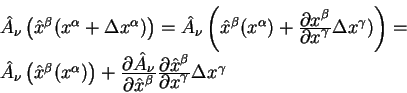
    \begin{displaymath} \begin{array}{l} \hat A_{\nu}\left(\hat x^{\beta}(x^{\alpha}... ...displaystyle\partial x^{\gamma}} \Delta x^{\gamma} \end{array}\end{displaymath}

    Все величины теперь вычислены в точке $x^{\alpha}$, поэтому можем строить дифференциал и производную векторного поля по обычным правилам:

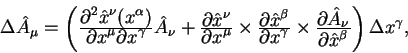
    \begin{displaymath} \begin{array}{l} \Delta \hat A_{\mu}= \left( {\displaystyle\... ...partial \hat x^{\beta}} \right) \Delta x^{\gamma}, \end{array}\end{displaymath}

    а производная этого векторного поля вычисляется как:

    \begin{displaymath} \begin{array}{l} {\displaystyle \partial \hat A_{\mu}\over\d... ... A_{\nu}\over\displaystyle\partial \hat x^{\beta}} \end{array}\end{displaymath}

    Второй член в этом уравнении обладает признаками тензора, преобразуется как тензорное поле второго ранга. Первое слагаемое явно не является тензорным полем, поскольку преобразуется по другим правилам.

    Так получилось потому, что мы пренебрегли последовательными рассуждениями в определении производных от векторнорго поля в неэвклидовой геометрии. При вычислении приращения векторного поля мы вычитали величины определенные в разных точках пространства. Первая величина определена в точке $x^{\alpha} +\Delta x^{\alpha}$, а вторая в точке $x^{\alpha}$. В эвклидовой геометрии при вычислении приращения векторного поля обычно опускается промежуточный шаг, который заключается в том, что векторы, заданные в соседних точках, сводятся по определенным правилам в одну точку.

    Таким правилом является параллельный перенос. Дифференциал векторного поля, полученный вычитанием значения векторного поля заданного в точке $x^{\alpha}$ и параллельно перенесенного из точки $x^{\alpha}$ в точку $x^{\alpha} +\Delta x^{\alpha}$ из значения векторного поля в точке $x^{\alpha} +\Delta x^{\alpha}$ называется ковариантным дифференциалом.

    Итак, для получения из тензорного поля ранга $n$ путем дифференцирования тензорного поля ранга $n-1$ необходимо вычислять не обычный дифференциал, а ковариантный дифференциал.

    6.1.1 Параллельный перенос вектора

    Ковариантное дифференцирование тесно связано с понятием параллельного переноса вектора.

    Параллельный перенос вектора в эвклидовом пространстве определяется как перенос вдоль некоторой прямой таким образом, что угол между вектором и прямой остается при переносе постоянным. Соответственно, компоненты вектора при таком переносе остаются неизменными.

    В неэвклидовой геометрии эта операция несколько изменяется. Аналогом прямой в неэвклидовой геометрии является геодезическая линия. Параллельный перенос вектора определяется как перенос вдоль геодезической линии, которая соединяет две точки. Естественно, как и в эвклидовой геометрии, угол между переносимым вектором и геодезической линией остается постоянным.

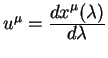    В качестве характеристики угла между выбранным вектором, скажем, $A_{\alpha}$ и геодезической линией принимем угол между вектором $A_{\alpha}$ и вектором касательным к геодезической линии. Таким вектором является производная от уравнений геодезической линии по афинному параметру вдоль этой линии $u^{\mu}={\displaystyle d x^{\mu}(\lambda)\over\displaystyle d \lambda}$. Угол между $A_{\alpha}$ и $u^{\alpha}$ определяется согласно уравнению (5.8). Пусть норма вектора $u^{\alpha}$ равна единице6.1. Прежде чем вести вычисления, заметим, что при параллельном переносе скалярные величины не меняются6.2. Поэтому скалярное произведение двух векторов тоже остается постоянным при параллельном переносе, а значит и норма одного вектора постоянна при таком переносе. Поэтому требование постоянства угла между вектором $u^{\alpha}$ и вектором $A_{\alpha}$ можно заменить на требование постоянства скалярного произведения этих векторов.

    Итак вычислим изменение произвольного вектора $A_{\alpha}$ при параллельном переносе вдоль геодезической линии. Основное требонание, налагаемое параллельным перносом заключается в том, что скалярное произведение вектора $A_{\alpha}$ и вектора касательного к геодезической линии является постоянным вдоль линии переноса:

    \begin{displaymath} A_{\alpha}(x^{\beta})u^{\alpha}(x^{\beta})=A_{\alpha}(x^{\beta} +\Delta x^{\beta}) u^{\alpha}(x^{\beta} +\Delta x^{\beta}) \end{displaymath}

    Введем обозначение для изменения компонент $\delta A_{\alpha}$ вектора при параллельном переносе. Теперь распишем уравнение сохрания скалярного произведения более подробно

    \begin{displaymath} A_{\alpha} u^{\alpha} =\left(A_{\alpha} +\delta A_{\alpha}\right) \left(u^{\alpha} + d u^{\alpha}\right) \end{displaymath}

    Преобразуем правую часть уравнения, выделив член нулевого порядка малости по бесконечно малому смещению и два члена первого порядка малости, вторым порядком малости здесь будем пренебрегать. Первый член в правой части сократится с членом, который стоит в левой части, а два члена первого порядка малости дадут уравнение для вычисления $\delta A_{\alpha}$:

    \begin{displaymath} u^{\alpha}\delta A_{\alpha}= - A_{\alpha} du^{\alpha} \end{displaymath}

    Подставим в это уравнение изменение касательного вектора вдоль геодезической (5.13) и получим уравнение для изменения вектора $\delta A_{\alpha}$:

    \begin{displaymath} u^{\alpha}\delta A_{\alpha}= A_{\alpha} \Gamma^{\alpha}_{\mu \nu} u^{\mu} u^{\nu} \end{displaymath}

    Отсюда получаем решение:

    \begin{displaymath} \delta A_{\mu}= \Gamma^{\alpha}_{\mu \beta} A_{\alpha} dx^{\beta} \end{displaymath}

    В современных [10] и классических курсах [8] по общей теории относительности уравнение для вычисления изменений компонент вектора при параллельном перносе выводится методом переноса вдоль прямой в касательном пространстве [10] или в галилеевых координатах [8]. Эти две операции эквивалентны. Параллельный перенос приводит к тому, что компоненты вектора меняются.

    Ковариантный дифференциал будем обозначать большой буквой $D$ латинского алфавита. Ковариантный дифференциал векторного поля $D A_{\mu}$ является разностью двух малых величин. Первая - обычный дифференциал поля $A_{\mu}$ между двумя пространственно - временными точками $d A_{\mu}$, вторая величина - изменение векторного поля $\delta A_{\mu}$ при параллельном переносе его из одной точки пространства в другую.

    \begin{displaymath} D A_{\mu}= d A_{\mu} - \delta A_{\mu} \end{displaymath}

    Контравариантные компоненты $\delta A^{\mu}$ от ковариантных отличаются знаком:

    \begin{displaymath} \delta A^{\mu}= -\Gamma^{\mu}_{\alpha \beta} A^{\alpha} dx^{\beta} \end{displaymath}

    Теперь можно написать уравнения для ковариантных дифференциалов

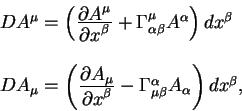
    \begin{displaymath} \begin{array}{l} D A^{\mu}= \left( {\displaystyle\partial A^... ...^{\alpha}_{\mu \beta} A_{\alpha} \right)dx^{\beta}, \end{array}\end{displaymath}

    а также уравнения для ковариантных производных от векторов

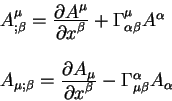
    \begin{displaymath} \begin{array}{l} A^{\mu}_{;\beta}= {\displaystyle\partial A... ...{\beta}} -\Gamma^{\alpha}_{\mu \beta} A_{\alpha} \end{array} \end{displaymath}

    Знак ";" означает ковариантную производную. Мы будем в дальнейшем использовать этот знак "точка с запятой" для обозначения ковариантной производной, а для обозначения обычной производной будем использовать знак "," - "запятая".

    Легко видеть, что ковариантный дифференциал $D$ подчиняется всем основным правилам дифференцирования:


    $\displaystyle D (C \cdot A_{\mu}) =C D A_{\mu}$  
    $\displaystyle D (A_{\mu} \pm B_{\mu}) =D A_{\mu} \pm D B_{\mu}$  
    $\displaystyle D (A_{\mu} \cdot B_{\nu}) =B_{\nu} \cdot D A_{\mu} +A_{\mu} \cdot D B_{\nu}$ (6.2)
    $\displaystyle D (A_{\mu} \cdot B^{\nu}) =B^{\nu} \cdot D A_{\mu} +A_{\mu} \cdot D B^{\nu},$  

    пользуясь этими правилами можно доказать правило образования ковариантных производных от тензоров более высокого ранга чем вектора:


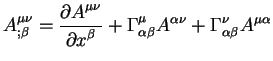    $\displaystyle A^{\mu \nu}_{;\beta}= {\displaystyle\partial A^{\mu \nu}\over\dis... ...{\mu}_{\alpha \beta} A^{\alpha \nu} +\Gamma^{\nu}_{\alpha \beta} A^{\mu \alpha}$ (6.3)
    $\displaystyle \qquad{}$ (6.4)
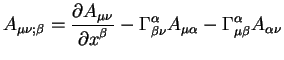    $\displaystyle A_{\mu \nu; \beta}= {\displaystyle\partial A_{\mu \nu}\over\displ... ...^{\alpha}_{\beta \nu} A_{\mu \alpha}-\Gamma^{\alpha}_{\mu \beta} A_{\alpha \nu}$ (6.5)
    $\displaystyle \qquad{}$ (6.6)
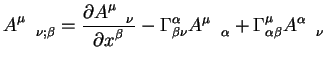    $\displaystyle A^{\mu}_{\quad \nu; \beta}= {\displaystyle\partial A^{\mu}_{\quad... ...\nu} A^{\mu}_{\quad \alpha} +\Gamma^{\mu}_{\alpha \beta} A^{\alpha}_{\quad \nu}$ (6.7)

    Обратим внимание, что в случае смещанных индексов порядок может быть важен, в том случае, когда тензор не является симметричным. Тогда указание на то, что индекс должен следовать вторым показано отступом, верхний и нижний индексы не расположены в одной колонке. То же самое справедливо и для символом Кристоффеля.

    Теперь можно просто сформулировать словесное правило образования ковари антной производной от тензора любого ранга и содержащего произвольное количество нижних и верхних индексов. Ковариантная производная равняется сумме частной производной от тензора по некоторой координате плюс (или минус) произведения символов Кристоффеля на сам тензор. Количество членов в этой сумме равняется количеству индексов плюс частная производная от самого тензора. Более точно, ковариантная производная от тензора ранга $m+n$, содержащего $m$ верхних и $n$ нижних индексов равняется частной производной от этого тензора, плюс произведение символа Кристоффеля (с верхним индексом таким же как один из верхних индексов дифференцируемого тензора и одним из нижних индексов таких же как у координаты, по которой ведется дифференцирование) с самим тензором у которого один из верхних индексов суммируется со вторым индексом символа Кристоффеля, минус произведение символа Кристофферя (теперь верхний индекс у связности является немым индексом суммирования, а один из нижних индексов такой же как у координаты по которой ведется дифференцирование) с самим тензором у которого очередный нижний индекс заменен на нем ой индекс суммирования, а остальные расположены по порядку.

    Коваринтные производные подчиняются тем же обычным правилам дифференцирования, которые справедливы для обычных производных от векторных и тензорных полей в эвклидовам пространстве. Эти правила перечислены чуть выше для вариаций вектора (см. уравнение (6.2)).

    Добавим, что ковариантная производная от скалярного поля совпадает с обычной производной.

    Законы преобразований символов Кристоффеля при преобразованиях координат имеют вид:

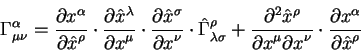
    \begin{displaymath} \Gamma^{\alpha}_{\mu \nu}={\displaystyle\partial x^{\alpha}\... ...le\partial x^{\alpha}\over\displaystyle\partial \hat x^{\rho}} \end{displaymath}

    В обычной неэвклидовой геометрии предпологается, что символ Кристоффеля является симметричным по нижним индексам.

    Существует обобщения неэвклидовой геометрии в которой символ Кристоффеля уже не является симметричным. Разность

    \begin{displaymath} S^{\alpha}_{\mu \nu} = \Gamma^{\alpha}_{\mu \nu} - \Gamma^{\alpha}_{\nu \mu} \end{displaymath}

    называется тензором кручения. В отличие от символа Кристоффеля, который не является тензором и преобразуется по закону, содержащему вторую производную от координат, величина $S^{\alpha}_{\mu \nu}$ является тензором и, как легко проверить, преобразуется как тензор третьего ранга.

    В общей теории относительности тензор кручения равен нулю, эксперименты показывают, что введение этой величины излишне. Поэтому далее мы не будем рассматривать тензор кривизны и его наблюдательные проявления. В общей теории относительности символ Кристоффеля является симметричным по нижним индексам, что выражается уравнением вида $\Gamma^{\alpha}_{\mu \nu}=\Gamma^{\alpha}_{\nu \mu}$. Всюду ниже будем полагать, что $\Gamma^{\alpha}_{\mu \nu}$ является симметричным по индексам ${ \bf\mu \nu}$.

    6.2 Связь метрического тензора и символов Кристоффеля

    Для вычисления ковариантных производных в неэвклидовой геометрии необходимо научиться вычислять символы Кристоффеля. Они вычисляются очень просто в метрических пространствах, когда $\Gamma^{\alpha}_{\mu \nu}$ определяется через метрический тензор. Найдем связь $\Gamma^{\alpha}_{\mu \nu}$ с метрическим тензором.

    Ковариантный дифференциал является тензором, поэтому согласно правилу поднятия и опускания индексов в метрических пространствах можно написать уравнение:
    \begin{displaymath} D A_{\mu}= g_{\mu \nu} D A^{\nu} \end{displaymath} (6.8)

    с другой стороны аналогичное уравнение можно написать для самих векторов
    \begin{displaymath} A_{\mu}= g_{\mu \nu} A^{\nu} \end{displaymath} (6.9)

    Теперь продифференцирум (6.9) и применим правила (6.2). Получим уравнение вида
    \begin{displaymath} D A_{\mu}= g_{\mu \nu} D A^{\nu} + A^{\nu} D g_{\mu \nu} \end{displaymath} (6.10)

    Из сравнений уравнений (6.8) и (6.10) видно, что ковариантный дифференциал от метрического тензора равен нулю. Следовательно равны нулю ковариантные производные по всем координатам. Вычислим ковариантные производные в явном виде согласно уравнению (6.5). Эти ковариантные производные имеют вид:
    \begin{displaymath} g_{\mu \nu; \beta}= {\displaystyle\partial g_{\mu \nu}\over\... ...u} g_{\mu \alpha }-\Gamma^{\alpha}_{\mu \beta} g_{\alpha \nu} \end{displaymath} (6.11)

    Поскольку левая часть уравнения (6.11) равна нулю, как это следует из уравнения (6.10), то и правая тоже равна нулю. В результате получаем линейное уравнение для связи символов Кристоффеля с метрическим тензором и его частными производными первого порядка:
    \begin{displaymath} {\displaystyle\partial g_{\mu \nu}\over\displaystyle\partial... ...g_{\mu \alpha }-\Gamma^{\alpha}_{\mu \beta} g_{\alpha \nu} =0 \end{displaymath} (6.12)

    Переставляя индексы в уравнении (6.12) получаем систему линейных уравнений вида:


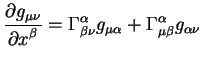    $\displaystyle {\displaystyle\partial g_{\mu \nu}\over\displaystyle\partial x^{\... ...\alpha}_{\beta \nu} g_{\mu \alpha } +\Gamma^{\alpha}_{\mu \beta} g_{\alpha \nu}$ (6.13)
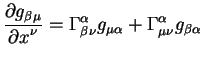    $\displaystyle {\displaystyle\partial g_{\beta \mu}\over\displaystyle\partial x^... ...\alpha}_{\beta \nu} g_{\mu \alpha } +\Gamma^{\alpha}_{\mu \nu} g_{\beta \alpha}$ (6.14)
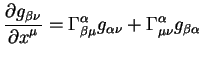    $\displaystyle {\displaystyle\partial g_{\beta \nu}\over\displaystyle\partial x^... ...{\alpha}_{\beta \mu} g_{\alpha \nu} +\Gamma^{\alpha}_{\mu \nu} g_{\beta \alpha}$ (6.15)

    Вычитая почленно из уравнения (6.13) уравнения (6.14) и (6.15), получаем уравнение

    \begin{displaymath} 2g_{\beta \alpha} \Gamma^{\alpha}_{\mu \nu}= {\displaystyle\... ...yle\partial g_{\mu \nu}\over\displaystyle\partial x^{\beta}} , \end{displaymath}

    из которого легко находим связь символов Кристоффеля с метрическим тензором и его первыми производными по координатам:
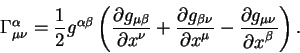    \begin{displaymath} \Gamma^{\alpha}_{\mu \nu}= {\displaystyle 1\over\displaystyl... ...tial g_{\mu \nu}\over\displaystyle\partial x^{\beta}}\right). \end{displaymath} (6.16)

    Как видно из уравнения (5.11) эти два символа совпадают.

    6.2.1 Ковариантная производная 4x скорости

    Рассмотрим теперь ковариантную производную одного из самых важных для нас векторов - 4$^x$ скорости пробной частицы или вектора касательного к геодезической линии. Ковариантный дифференциал этого вектора есть:

    \begin{displaymath} D u^{\alpha} = d u^{\alpha} + \Gamma^{\alpha}_{\mu \nu} u^{\mu} d x^{\nu} \end{displaymath}

    Теперь можно вычислить частную ковариантную производную по одной из координат:

    \begin{displaymath} u^{\alpha}_{; \nu} = {\displaystyle\partial u^{\alpha}\over\... ...aystyle\partial x^{\nu}} + \Gamma^{\alpha}_{\mu \nu} u^{\mu} \end{displaymath}

    в соответствии с общими правилами ковариантного дифференцирования. Умножим это уравнение на сам вектор 4$^x$ скорости:

    \begin{displaymath} u^{\alpha}_{; \nu} u^{\nu} = {\displaystyle\partial u^{\alph... ...x^{\nu}} u^{\nu} + \Gamma^{\alpha}_{\mu \nu} u^{\mu} u^{\nu} \end{displaymath}

    Первый член в правой части этого уравнения, как легко видеть, равен полной производной от скорости по афинному параметру вдоль геодезической линии:

    \begin{displaymath} {\displaystyle\partial u^{\alpha}\over\displaystyle\partial ... ... u^{\nu} = {\displaystyle d u^{\alpha}\over\displaystyle d s} \end{displaymath}

    Оба члена вместе представляют уравнение геодезической линии, откуда имеем еще один вид уравнения геодезической:
    \begin{displaymath} u^{\alpha}_{\quad ; \mu} \; u^{\mu} =0 \end{displaymath} (6.17)

    6.3 Производная Лагранжа -Эйлера

    В математическом анализе и геометрии используют еще несколько видов производных. Для нас важными являются две из них, это производная Лагранжа -Эйлера и производная Ли. Вначале познакомимся с производной Лагранжа -Эйлера.

    Рассмотрим множество функций $\Phi_{A}(x^{\alpha})$ координат $x^{\alpha}$. Эти функции могут быть компонентами скаляра, вектора или тензора. Они могут быть объектами другой природы, которые преобразуются к другой системе координат по собственным правилам. Для вычисления производной Лагранжа -Эйлера неважна природа этих функций. Мы опустим индекс $A$, но будем помнить, что функции $\Phi$ представляют из себя набор функций.

    Рассмотрим функцию $\bf L$ от аргументов, которые сами являются функциями и их производными:


    \begin{displaymath} {\bf L}(\Phi, \Phi_{, \mu}, \Phi_{, \mu, \nu}, \Phi_{, \mu, \nu, \xi}, \mbox{ и так далее}) \end{displaymath}

    Еще раз подчеркнем, что $\Phi$ в общем случае является множеством функций, а не обязательно одной функцией.

    Рассмотрим теперь функционал, например действие от функции ${\bf L}$:

    \begin{displaymath} S = \int {\bf L} d^4 x \end{displaymath}

    взятое по некоторой 4$^x$ области $\Omega$.

    Обозначим $\delta \Phi$ вариацию поля $\Phi$ и будем считать, что вариации самого поля, а также всех его производных исчезают на границе области $\Omega$.

    Вариации функции ${\bf L}$ имеют вид:

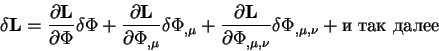
    \begin{displaymath} \delta {\bf L}={\displaystyle\partial {\bf L}\over\displayst... ...i_{, \mu, \nu}} \delta \Phi_{, \mu, \nu} + \mbox{и так далее} \end{displaymath}

    Отсюда получаем для вариаций функционала уравнение вида:

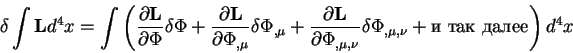
    \begin{displaymath} \delta \int {\bf L} d^4 x = \int \left( {\displaystyle\parti... ...} \delta \Phi_{, \mu, \nu} + \mbox{и так далее} \right) d^4 x \end{displaymath}

    Интегрируя каждый из членов в круглых скобках по частям получаем:

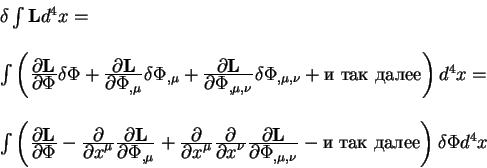
    \begin{displaymath} \begin{array}{l} \delta \int {\bf L} d^4 x = \\ \qquad \\ ... ...} - \mbox{и так далее} \right) \delta \Phi d^4 x \end{array} \end{displaymath}

    Выражение, которое находится в круглых скобках в последней строчке называется производной Лагранжа -Эйлера. Итак по определению величина:

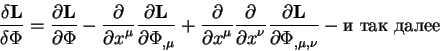
    \begin{displaymath} {\displaystyle\delta {\bf L}\over\displaystyle\delta \Phi} =... ...\displaystyle\partial \Phi_{, \mu, \nu}} - \mbox{и так далее} \end{displaymath}

    называется производной Лагранжа -Эйлера от L. Она тесно связана c функциональной или вариационной производной вводимой в теории случайных полей [11].

    Уравнение вида:

    \begin{displaymath} {\displaystyle\delta {\bf L}\over\displaystyle\delta \Phi} = 0 \end{displaymath}

    называется уравнением Эйлера. Уравнения такого вида являются уравнениями движения в ньютоновской механике. Иногда в качестве величины $\Phi$ выступает переменная, которая вообще не преобразуется.

    6.4 Производная Ли

    Производная Ли для нас не так важна, как производная Лагранжа - Эйлера, но все же мы кратко проанализируем ее здесь, поскольку будем обращаться к ней несколько раз в течение курса. Более подробно о методе Ли и его применениях будет рассказано ниже.

    Производная Ли играет большое значение при исследовании свойств симметрии метрики. Для исследования этих свойств напомним вначале простейшее понятие симметрии, например зеркальной симметрии. Геометрическое тело называют симметричным относительно плоскости, если эта плоскость разбивает тело на две части, из которых каждая является зеркальным отражением другой относительно этой плоскости. Сама плоскость в этом случае называется плоскостью симметрии. Зеркальной симметрией обладают многие предметы из окружающего нас мира: самолет, лист клена, форма человеческого тела (внутреннее строение уже не обладает свойством зеркальной симметрии!).

    С формальной точки зрения зеркальную симметрию определяют как форминвариантность относительно преобразования координат вида:

    \begin{displaymath} x \rightarrow -x \hskip0.3cm . \end{displaymath}

    Если при таком преобразовании координат форма тела остается неизменной, то говорят, что геометрическое тело симметрично относительно плоскости $Oyz$

    Отметим, что приведенное выше преобразование не является непрерывным относительно некоторого параметра, как в большинстве случаев, которые мы рассматривали при преобразованиях координат в неэвклидовой геометрии. Поэтому свойства симметрии геометрических тел, точнее функций связаны с инвариантностью при преобразованиях координат. Зеркальная симметрия относиться к так называемым дискретным видам симметрии.

    Ниже мы будем рассматривать только точечные виды симметрии. Они связаны с непрерывными преобразованиями, непрерывно зависят от одного или нескольких параметров. К таким видам симметрии относится, например, симметрия относительно вращения. Так, сфера - идеальный объект в трехмерном пространстве для изучения группы вращений. Вращения можно осуществлять на произвольный, сколь угодно малый, угол.

    Определим понятие симметрии для метрического тензора. Говорят, что метрика $g_{\mu \nu}$ является форминвариантной относительно преобразований координат вида $\tilde x^{\mu}=f^{\mu}(x^{\alpha})$, если преобразованная метрика $\tilde g_{\mu \nu}(\tilde x^{\alpha})$ - та же функция от аргумента $\tilde x^{\mu}$, что и первоначальная функция $ g_{\mu \nu}( x^{\alpha})$ от ее первоначального аргумента $x^{\alpha}$, т.е. [12]

    \begin{displaymath} \tilde g_{\mu \nu}(\tilde x^{\alpha}) = g_{\mu \nu}( x^{\alpha}) \hskip1cm \mbox{для всех } x^{\alpha} \end{displaymath}

    Заметим, что это равенство можно также переписать в двух эквивалентных формулировках:


    \begin{displaymath} \tilde g_{\mu \nu}( x^{\alpha}) = g_{\mu \nu}( x^{\alpha}) \hskip1cm \mbox{для всех } x^{\alpha} \end{displaymath}

    и


    \begin{displaymath} \tilde g_{\mu \nu}(\tilde x^{\alpha}) = g_{\mu \nu}(\tilde x^{\alpha}) \hskip1cm \mbox{для всех } \tilde x^{\alpha} \end{displaymath}

    Многие геометрические свойства пространства можно определить пользуясь понятиями симметрии. Симметрии пространства также важны для определения физических свойств, законов сохранения, поиска наиболее общих интегралов уравнений движения. Свойства метрики пространства - времени можно определить не прибегая к решению уравнений общей теории относительности, а пользуясь только соображениями симметрии. Поясним как это можно сделать на примере производных Ли.

    Производные Ли являются обощениями понятия производных по направлению на тензоры. Рассмотрим две точки в пространстве $P_0$ и $P_1$, разделенные малым расстоянием. Пусть координаты этих точек соединяются бесконечно малым вектором, квадратом которого можно пренебречь по сравнению с самим вектором6.3:

    \begin{displaymath} x^{\mu}(P_1) = x^{\mu}(P_0) + \xi^{\mu} \end{displaymath}

    Пусть задано некоторое скалярное поле $\Phi(x^{\alpha})$. Вычислим значение поля $\Phi$ в точке $P_1$ если значение этого поля в точке $P_0$ задано:

    \begin{displaymath} \Phi(P_1) = \Phi(P_0) + \xi^{\mu} {\displaystyle\partial \Phi\over\displaystyle\partial x^{\mu}} \end{displaymath}

    Естественно, в этом разложении $\Phi(P_1)$ в ряд Тейлора можно пренебречь квадратичными поправками и поправками более высоких степеней. Величина:
    \begin{displaymath} {\cal L}_{\xi} \Phi = \xi^{\mu} {\displaystyle\partial \Phi\over\displaystyle\partial x^{\mu}} \end{displaymath} (6.18)

    называется производной Ли от скалярного поля. В курсах высшей математики этот оператор чаще называется производной по направлению $\xi^{\mu}$.

    Рассмотрим смысл такой производной на примере скалярного поля, заданного в трехмерном пространстве. Пусть у нас задано цилиндрически - симметричное распределение температуры в пространстве с цилиндрическими координатами $Oz$, $r$ и $\varphi$. Интуитивно понятно, что температура может зависеть от радиуса $r$, но она не будет зависеть от координаты $Oz$ или от координаты $\varphi$. Это означает, что производная от температуры по координатам $z$, $\varphi$ равна нулю. В инвариантном виде это означает, что существуют вектора, выделяющие направление вдоль которых производная Ли равна нулю. В данном частном случае это вектора описывающие движения вдоль оси $Oz$ и вокруг нее. В общем случае движение, которое описывает вектор $\xi^{\mu}$, описывает точечную симметрию, если значение поля $\Phi$ в двух точках $P_0$ и $P_1$ вдоль этого вектора является постоянным.

    Теперь определим производную Ли для векторного поля $A^{\mu}(x^{\nu})$. От случая скалярного поля эта производная отличается тем, что теперь вычисляется величина, которая зависит от координатной системы. Итак, вновь у нас есть две точки, которые разделены бесконечно малым вектором $\xi^{\mu}$. Значения векторного поля в точке $P_1$ через значения в точке $P_0$ вычисляются как:

    \begin{displaymath} A^{\mu}(P_1) = A^{\mu}(P_0) + \xi^{\alpha} {\displaystyle\partial A^{\mu}\over\displaystyle\partial x^{\alpha}} \end{displaymath}

    Рассмотрим теперь преобразование координат:

    \begin{displaymath} \tilde x^{\alpha} = x^{\alpha} + \xi^{\alpha} (x), \end{displaymath}

    где $\xi^{\alpha}$ - тот же самый вектор бесконечно малой величины. Теперь, как нетрудно видеть, точка $P_1$ имеет те же значения координат в тильдованной системе, что и точка $P_0$ в нетильдованной системе. Коэффиценты в матрице преобразования векторов для такого преобразования имеют вид:

    \begin{displaymath} {\displaystyle\partial \tilde x^{\alpha}\over\displaystyle\p... ...partial \xi^{\alpha}(x)\over\displaystyle\partial x^{\beta}} \end{displaymath}

    Соответственно коэффиценты в матрице преобразования вектора в точке $P_1$ есть:

    \begin{displaymath} \tilde A^{\mu}(P_1) = {\displaystyle\partial \tilde x^{\mu}\over\displaystyle\partial x^{\nu}} A^{\nu}(P_1) \end{displaymath}

    или

    \begin{displaymath} \tilde A^{\mu}(P_1) = \left( \delta^{\mu}_{\nu} + \xi^{\mu},_{\nu}\right) A^{\nu}(P_1) \end{displaymath}

    Запищем теперь значение вектора в точке $P_1$ через значение в точке $P_0$, тогда получим:

    \begin{displaymath} \tilde A^{\mu}(P_1) = A^{\mu}(P_0) + \xi^{\alpha} {\displays... ...playstyle\partial x^{\alpha}} + \xi^{\mu},_{\nu} A^{\nu}(P_0) \end{displaymath}

    Разница между преобразованными компонентами векторного поля в точке $P_1$ и непреобразованными компонентами векторного поля в точке $P_0$ называется дифференциалом Ли или производной Ли:
    \begin{displaymath} {\cal L}_{\xi} A^{\mu} = \xi^{\alpha} {\displaystyle\partial... ...r\displaystyle\partial x^{\alpha}} + \xi^{\mu},_{\nu} A^{\nu} \end{displaymath} (6.19)

    Аналогично можно определить производную Ли для тензорного поля. Рассмотрим теперь какое - либо тензорное поле, например, образованное из тензора второго ранга, которое в системе координат без тильды имеет компоненты $U^{\alpha \beta} (x)$. В преобразованной системе координат оно имеет вид:

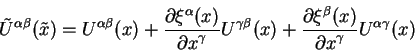
    \begin{displaymath} \tilde U^{\alpha \beta} (\tilde x) = U^{\alpha \beta} ( x) ... ...)\over\displaystyle\partial x^{\gamma}} U^{\alpha \gamma} (x) \end{displaymath}

    Так отличаются компоненты тензора ${\bf U}$ в тильдованной и нетильдованной системах координат. Теперь вычислим компоненты этого тензора в точках $P_1$ и $P_0$.

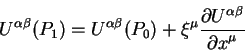
    \begin{displaymath} U^{\alpha \beta}(P_1) = U^{\alpha \beta}(P_0) + \xi^{\mu}{\d... ...\partial U^{\alpha \beta}\over\displaystyle\partial x^{\mu}} \end{displaymath}

    Окончательно вычислим разницу между значениями компонент тензора в точке $P_0$ в нетильдованной системе координат и значениями компонент тензора в точке $P_1$ в тильдованной системе координат. Эта величина называется производной Ли для тензоров второго ранга:
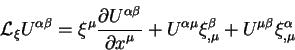    \begin{displaymath} {\cal L}_{\xi} U^{\alpha \beta} = \xi^{\mu}{\displaystyle\pa... ...pha \mu} \xi^{\beta}_{,\mu} +U^{\mu \beta} \xi^{\alpha}_{,\mu} \end{displaymath} (6.20)

    Теперь можно определить симметрию тензорного поля ${\bf U}$ относительно векторного поля $\xi^{\mu}$ как равенство нулю производной Ли (6.20).

    Вернемся теперь к симметриям метрического тензора. Производная Ли метрического тензора выглядит особенно просто:
    \begin{displaymath} {\cal L}_{\xi} g_{\mu \nu} =- \xi_{\mu ; \nu} - \xi_{\nu ; \mu} \end{displaymath} (6.21)

    Это просто проверяется непосредственным вычислением. Равенство нулю производной Ли дает нам уравнение Киллинга:
    \begin{displaymath} \xi_{\mu ; \nu} + \xi_{\nu ; \mu} = 0 , \end{displaymath} (6.22)

    которое определяет симметрии метрического тензора.

    8. Уравнение движения в >>

    Разделы

    7. Тензор кривизны

    Неэвклидова геометрия полностью характеризуется метрическим тензором. Однако помимо этого тензора существует еще несколько важных тензоров, которые тоже используются для характеристики важных соотношений неэвклидовой геометрии. Самой важной величиной после метрического тензора является тензор кривизны или, как для краткости говорят релятивисты, кривизна. Тензор кривизны можно вводить несколькими путями. Мы обсудим здесь два способа определения тензора кривизны. Первый способ - через вторые ковариантные производные от вектора, второй способ более традиционный - посредством сравнения ковариантного переноса вектора по двум путям, образующим замкнутую кривую.

    7.1 Тензор кривизны

    7.1.1 Вторые ковариантные производные

    Пусть в нашем пространстве задано векторное поле $A_{\mu}(x^{\alpha})$. Рассмотрим первые производные этого векторного поля и вторые производные поля $A_{\mu}(x^{\alpha})$. Поскольку большинство уравнений математической физики - уравнения содержащие вторые производные от физической величины, то при обобщении уравнений описывающих какое - либо поле, например, электромагнитное, нам придется выводить уравнения, которые содержат вторые производные от полей по координатам. В эвклидовой геометрии порядок производных был неважен, производные обладали свойством коммутации. В неэвклидовой геометрии это свойство, вообще говоря, теряется.

    Рассмотрим ковариантные производные второго порядка. Такую производную можно записать как
    \begin{displaymath} A_{\mu; \alpha; \beta} ={\displaystyle\partial A_{\mu; \alph... ..._{\rho; \alpha} - \Gamma^{\rho}_{\alpha \beta} A_{\mu; \rho}, \end{displaymath} (7.1)

    так как $A_{\mu; \alpha}$ является тензором второго ранга. Теперь подставим уравнение для первой ковариантной производной в (7.1) и получим уравнение вида:

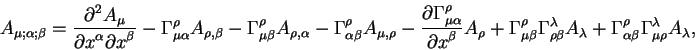
    \begin{displaymath} A_{\mu; \alpha; \beta} ={\displaystyle\partial^2 A_{\mu}\ove... ...rho}_{\alpha \beta} \Gamma^{\lambda}_{\mu \rho} A_{\lambda} , \end{displaymath}

    в этой формуле, как и прежде, точка с запятой перед индексом означают ковариантное дифференцирование по координате именуемой этим индексом, запятая - частную производную по координате с одноименным индексом.

    Теперь выпишем разность ковариантных производных меняя индексы по которым ведется дифференцирование.


    $\displaystyle A_{\mu; \alpha; \beta} -A_{\mu; \beta; \alpha} =$ (7.2)
    $\displaystyle \qquad$  
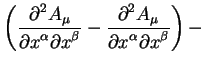    $\displaystyle \left({\displaystyle\partial^2 A_{\mu}\over\displaystyle\partial ... ...ial^2 A_{\mu}\over\displaystyle\partial x^{\alpha} \partial x^{\beta}}\right) -$  
    $\displaystyle \qquad$  
    $\displaystyle - \Gamma^{\rho}_{\mu \alpha} A_{\rho, \beta} - \Gamma^{\rho}_{\mu... ...ho}_{\mu \alpha} A_{\rho, \beta} + \Gamma^{\rho}_{\beta \alpha} A_{\mu, \rho} -$  
    $\displaystyle \qquad$  
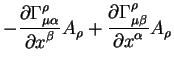    $\displaystyle - {\displaystyle\partial \Gamma^{\rho}_{\mu \alpha}\over\displays... ...artial \Gamma^{\rho}_{\mu \beta}\over\displaystyle\partial x^{\alpha}} A_{\rho}$  
    $\displaystyle \qquad$  
    $\displaystyle + \Gamma^{\rho}_{\mu \beta} \Gamma^{\lambda}_{\rho \beta} A_{\lam... ...mbda} - \Gamma^{\rho}_{\beta \alpha } \Gamma^{\lambda}_{\mu \rho} A_{\lambda} ,$  

    Проанализируем полученное уравнение. Прежде всего обратим внимание, что в левой части уравнения первая строчка, которая содержит антикоммутатор от частным производных обращается в ноль. Таким образом антикоммутатор ковариантных производных понижает порядок дифференцирования. Вторая строчка содержит первые частные производные от векторного поля. Заметим, что первый и пятый члены взаимно сокращаются, также сокращаются поочередно второй и четвертый, а также третий и шестой члены. Таким образом антикоммутатор ковариантных производных второго порядка не содержит частных производных вообще. Однако, уравнение (7.2) не обращается в ноль тождественно.

    Третья строчка полученного уравнения, которая содержит произведения частных производных от символа Кристоффеля на векторное поле не обращется в ноль тождественно. В последней строчке взаимно сокращаются второй и четвертый члены, но первый и третий члены не сокращаются. Таким образом, получается, что антикоммутатор ковариантных производных второго порядка равен произведению самого векторного поля на величину содержащую четыре индекса:
    \begin{displaymath} A_{\mu; \alpha; \beta} -A_{\mu; \beta; \alpha} = \\ \qquad \\ R^{\rho}_{. \mu \alpha \beta} A_{\rho} \end{displaymath} (7.3)

    Теперь легко доказать, что величина $R^{\rho}_{. \mu \alpha \beta}$ является тензором. Действительно, сделаем преобразование координат из одной системы (скажем, $\lbrace x^{\mu}\rbrace$) в другую $\lbrace \hat x^{\mu}\rbrace$. Слева в уравнении (7.3) стоит тензорная величина третьего ранга (напомним, что первая ковариантная производная от вектора является тензором второго ранга, соответственно вторая ковариантная производная от вектора является тензором третьего ранга). Справа в этом уравнении - произведение вектора на величину с четырьмя индексами. Сравнивая зависимость в двух системах координат получаем закон преобразования для $R^{\rho}_{. \mu \alpha \beta}$ в виде:

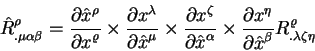
    \begin{displaymath} \hat R^{\rho}_{. \mu \alpha \beta} = {\displaystyle\partial... ...e\partial \hat x^{\beta}} R^{\varrho}_{. \lambda \zeta \eta} \end{displaymath}

    Это доказывает, что величина $R^{\rho}_{. \mu \alpha \beta}$ является тензором четвертого ранга.

    Этот тензор называется тензором кривизны или тензором Римана7.1. Его можно записать в виде уравнения в частных производных символов Кристоффеля и бинарных произведений символов.
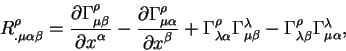    \begin{displaymath} R^{\rho}_{. \mu \alpha \beta} = {\displaystyle\partial \Gamm... ... \Gamma^{\rho}_{\lambda \beta} \Gamma^{\lambda}_{\mu \alpha}, \end{displaymath} (7.4)

    Здесь знаки в определении тензора кривизны выбраны так, чтобы тензор совпадал с определением принятым в [8]. Некоторые авторы определяют тензор Римана с противоположным знаком.

    7.2 Параллельный перенос вектора по замкнутой кривой

    В этой части мы рассмотрим второй, традиционный вывод тензора кривизны. В классических книгах, посвященных неэвклидовой геометрии и общей теории относительности, тензор кривизны появляется при обсуждении параллельного переноса вектора по замкнутой кривой (см. например, [8], [10]).

    Итак, рассмотрим параллельный перенос вектора вдоль замкнутой кривой. Для пояснения выкладок вначале выберем двумерную поверхность сферы, а в качестве вектора единичный вектор касательный к траектории переноса в начальной точке. Кривую нарисуем на поверхности сферы и будем считать, что эта кривая - параллель или линия широты.

    7.2.1 Параллельный перенос вектора по линии широты на сфере

    Метрику в координатах $\theta, \varphi$ можно записать как (5.9):

    \begin{displaymath} ds^2=d\theta^2 +\sin^2\theta d\varphi^2, \end{displaymath}

    а метрический тензор будет иметь вид

    \begin{displaymath} g_{\alpha \beta}= \left( \begin{array}{cc} 1& 0 \\ 0& \sin^2 \theta\\ \end{array} \right) \end{displaymath}

    Кроме того, выпишем вновь также компоненты символа Кристоффеля на поверхности единичной сферы:

    \begin{displaymath} \Gamma^1_{22}=- \sin \theta \cos \theta \qquad \Gamma^2_{12}= \ctg \theta \end{displaymath}

    Вектор $A$ переносится вдоль широты на сфере параллельно. Это значит, что ковариантная производная этого вектора вдоль выбранной кривой равна нулю. Поэтому формально условие параллельного перноса записывается как:

    \begin{displaymath} D A^{a} =0. \end{displaymath}

    Теперь напишем это формальное условие более детально:
    \begin{displaymath} d A^{a} = \Gamma^{a}_{m n} A^{m} d x^{n} \end{displaymath} (7.5)

    Пусть на параллели, которая характеризуется одним параметром - координатой $\theta=\theta_0$, задан вектор единичной длины:
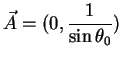    $\displaystyle \vec A =(0, {\displaystyle 1\over\displaystyle\sin \theta_0})$ (7.6)
    $\displaystyle (\vec A \vec A) = (A^1)^2 + \sin^2 \theta_0 (A^2)^2 =1$ (7.7)

    Вектор переносится вдоль широты, а это значит, что изменение координаты $\theta$ отсутствует, $d \theta =0$. Уравнения (7.5) принимают вид:
    $\displaystyle d A^1 = \sin \theta_0 \cos \theta_0 A^2 d \varphi$ (7.8)
    $\displaystyle d A^2 = -\ctg \theta_0 A^1 d \varphi$ (7.9)

    Вначале рассмотрим вспомогательный пример. Сдвинем вектор $A^a$ вдоль широты на расстояние $\Delta \varphi$. Его компоненты изменятся. Появится компонента направленная вдоль первой оси:

    \begin{displaymath} \Delta A^1={1 \over 2}\sin 2\theta_0 \Delta \varphi, \end{displaymath}

    а компонента вдоль второй оси останется неизменной (с точностью до малых величин второго порядка):

    \begin{displaymath} A^2(\varphi +\Delta \varphi) = {1 \over \sin \theta_0} \end{displaymath}

    Теперь видно, что вектор повернулся ( поскольку появилась компонента вдоль первой оси). Угол между параллельно перенесенным вектором и вектором, касательным к широте есть:

    \begin{displaymath} \cos \psi =\cos \theta_0 \Delta \varphi. \end{displaymath}

    Рассмотрим теперь математические операции более подробно и решим уравнения параллельного переноса вектора для вычисления его компонент после перенесения на конечное расстояние вдоль широты. Уравнения (7.8) становятся:
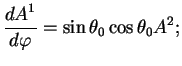    $\displaystyle {\displaystyle d A^1\over\displaystyle d \varphi} = \sin \theta_0 \cos \theta_0 A^2;$ (7.10)
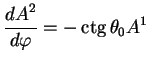    $\displaystyle {\displaystyle d A^2\over\displaystyle d \varphi} = - \ctg \theta_0 A^1$ (7.11)

    Теперь уравнения описывающие параллельный перенос вектора - это два обыкновенных дифференциальных уравнения. Продифференцируем второе из уравнений (7.10) по переменной $\varphi$ и подставим его в первое. Получим одно уравнение второго порядка:

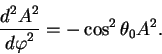
    \begin{displaymath} {\displaystyle d^2 A^2\over\displaystyle d \varphi^2} = - \cos^2 \theta_0 A^2. \end{displaymath}

    Его решение - это решение уравнения колебаний, когда частота колебаний равна $\cos \theta_0$. Это решение имеет вид:

    \begin{displaymath} A^2 (\varphi) = A_0 \cos (\varphi \cos \theta_0) + A_1 \sin( \varphi \cos \theta_0) \end{displaymath}

    Естественно, что решение зависит от двух постоянных величин $A_0$ и $A_1$.

    Соответственно решение для первой компоненты вектора получается дифференцированием по $\varphi$ и умножением на $- \tg \theta_0$:


    \begin{displaymath} A^1 (\varphi) = A_0 \sin \theta_0 \sin (\varphi \cos \theta_0) - A_1 \sin \theta_0 \cos( \varphi \cos \theta_0) \end{displaymath}

    Найдем теперь постоянные $A_0$ и $A_1$. В точке $\varphi =0$ компоненты вектора есть $A^1=0$, $A^2={\displaystyle 1\over\displaystyle\sin \theta_0}$. Подставим эти условия в найденные решения для компонент и получим, что $A_0={\displaystyle 1\over\displaystyle\sin \theta_0}$, а $A_1=0$. Поэтому решения для компонент вектора имеют вид:

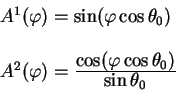
    \begin{displaymath} \begin{array}{l} A^1(\varphi) = \sin( \varphi \cos \theta_0)... ...rphi \cos \theta_0)\over\displaystyle\sin \theta_0} \end{array}\end{displaymath}

    Найдем угол между вектором $\vec A$ и единичным вектором, касательным к линии широты $\vec u =(0, {\displaystyle 1\over\displaystyle\sin \theta_0})$. Этот угол будет определяться уравнением:

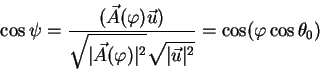
    \begin{displaymath} \cos \psi = {\displaystyle(\vec A(\varphi) \vec u)\over\disp... ...rt^2}\sqrt{\vert\vec u\vert^2}} = \cos (\varphi \cos \theta_0) \end{displaymath}

    Проекция вектора $\vec A$ на вектор $\vec u$ уменьшается по мере переноса $\vec A$ вдоль широты. В то же время проекция вектора $\vec A$ на единичный вектор вдоль меридиана, назовем его $\vec v =(1, 0)$ растет:

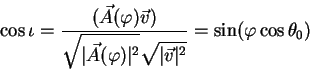
    \begin{displaymath} \cos \iota = {\displaystyle(\vec A(\varphi) \vec v)\over\dis... ...rt^2}\sqrt{\vert\vec v\vert^2}} = \sin (\varphi \cos \theta_0) \end{displaymath}

    Вектор, касательный к линии меридиана направлен от полюса. Посмотрим на сферу со стороны северного полюса. Пусть перенос осуществляется в направлении против часовой стрелки. Тогда поворот вектора $\vec A$ происходит по часовой стрелке.

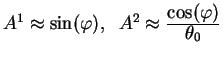    Рассмотрим более подробно перенос вектора по широте расположенной близко к полюсу. Будем считать, что $\theta_0 \approx 0$, и будем пренебрегать членами квадратичными по широте. Тогда $A^1 \approx \sin(\varphi), \; \; A^2 \approx {\displaystyle\cos(\varphi)\over\displaystyle\theta_0}$. Рассмотрим значения компонент в точке $\varphi={\displaystyle\pi\over\displaystyle 2}$. При этом видно, что компонента, направленная вдоль $\vec u$ обращается в ноль, а компонента, направленная вдоль вектора $\vec v$ становиться почти единичной. При переносе вдоль широты значительно отстоящей от полюса, компонента $\vec A$ вдоль $\vec u$ обращается в ноль при значении угла $\varphi ={\displaystyle\pi\over\displaystyle 2 \cos \theta_0}$.

    При дальнейшем переносе угол между $\vec A$ и $\vec u$ продолжает расти. После полного переноса вектора $\vec A$ и возвращения его в точку $\varphi =0$ угол между перенесенным вектором и вектором $\vec u$ есть:

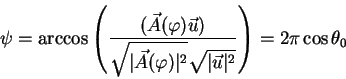
    \begin{displaymath} \psi =\arccos\left( {\displaystyle(\vec A(\varphi) \vec u)\o... ...\vert^2}\sqrt{\vert\vec u\vert^2}}\right) = 2\pi \cos \theta_0 \end{displaymath}

    Отметим также, что угол между исходным положением вектора и его конечным положением есть

    \begin{displaymath} 2\pi (1 - \cos \theta_0), \end{displaymath}

    что в точности равно площади сегмента сферы единичного радиуса, ограниченного линией широты.

    Если вектор переносится параллельно самому себе на плоскости вдоль замкнутой кривой, то после возвращения в исходную точку, вектор совпадает сам с собой. В неэвклидовой геометрии это не так. Следовательно геометрия на сфере неэквивалентна геометрии на плоскости. Чуть ниже мы увидим, что выведенные уравнения имеют отношение к кривизне поверхности.

    Рассмотрим теперь параллельное перенесение вектора вдоль замкнутой кривой в произвольной неэвклидовой геометрии.

    7.2.2 Перенос вектора по бесконечно малому параллелограмму

    Прежде чем исследовать поведение вектора $\vec A$ при параллельном перносе вдоль замкнутой кривой произвольной формы, мы рассмотрим перенос этого вектора вдоль бесконечно малого параллелограмма построенного на отрезках соответствующих координат.

    Рисунок 7.1: На рисунке изображен бесконечно малый параллелограмм. Вершины параллелограмма обозначены буквами $A, B, C, D$.
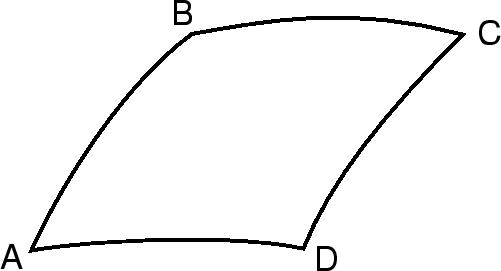    \begin{figure}\centerline{\epsfxsize=0.7\textwidth\epsfbox{fig7_1.ai}}\end{figure}

    Итак, пусть у нас задан вектор $A^{\alpha}$. Вершины параллелограмма обозначим $A, B, C, D$ (см. рис. 7.1). Точку $A$ и точку $B$ соединяет бесконечно малый вектор $d x^{\mu}_2$. Точку $A$ и точку $C$ соединяет бесконечно малый вектор $d x^{\mu}_1$. Поскольку наша фигура - параллелограмм, то стороны, противоположные сторонам $AB$ и $AC$ соединяют вектора полученные параллельным переносом. Сторона, которая построена на векторе соединяющем точки $B$ и $D$, противоположна стороне построенной на векторе $d x^{\mu}_1$. Этот вектор, параллельно перенесенный на $d x^{\mu}_2$, есть $d x^{\mu}_1 - \Gamma^{\mu}_{\alpha \beta} d x^{\alpha}_1 d x^{\beta}_2$. Сторона, которая построена на векторе, соединяющем точки $C$ и $D$, противоположна стороне, построенной на векторе $d x^{\mu}_2$. Этот вектор, параллельно перенесенный на $d x^{\mu}_1$, есть $d x^{\mu}_2 - \Gamma^{\mu}_{\alpha \beta} d x^{\alpha}_2 d x^{\beta}_1$. Таким образом мы вычислили размер сторон параллелограмма.

    Вычислим теперь изменение компонент вектора при перенесении. Пусть вектор $A^{\alpha}$ заданный в точке $A$ переносится параллельно самому себе вначале через точку $B$ в точку $D$, а затем из точки $A$ через точку $C$ в точку $D$.

    Рассмотрим вначале перенос из $A$ в $D$ через точку $B$. Величина вектора, перенесенного в $B$ есть:

    \begin{displaymath} A^{\alpha} - \Gamma^{\alpha}_{\mu \nu} A^{\mu} d x^{\nu}_2 \end{displaymath}

    Теперь этот вектор должен быть перенесен из точки $B$ в точку $D$. Но в точке $B$ значения символов Кристоффеля уже другие:

    \begin{displaymath} \Gamma^{\alpha}_{\mu \nu} +dx^{\xi} {\displaystyle\partial \Gamma^{\alpha}_{\mu \nu}\over\displaystyle\partial x^{\xi}} \end{displaymath}

    После перенесения из точки $B$ в $D$ вектор вновь изменяется. Следовательно вектор, перенесенный из $A$ в $D$ через $B$ имеет вид:

    \begin{displaymath} \begin{array}{l} A^{\alpha} - \Gamma^{\alpha}_{\mu \nu} A^{\... ...a}_{\lambda \rho} \Gamma^{\rho}_{\mu \nu }\right) \end{array} \end{displaymath}

    Здесь мы пренебрегли величинами третьего порядка малости.

    Для вектора перенесенного из $A$ в $D$ через точку $C$ получаем аналогичное выражение, в котором вектора $d x^{\mu}_1$ и $d x^{\mu}_2$ меняются местами. Теперь можно вычислить разность между двумя векторами, перенесенными в $D$ по двум траекториям. Эта разность равна:
    \begin{displaymath} d x^{\mu}_1 d x^{\nu}_2 \lbrace {\displaystyle\partial \Gamm... ...ha}_{\mu \rho} \Gamma^{\rho}_{\nu \lambda}\rbrace A^{\lambda} \end{displaymath} (7.12)

    Это выражение является вектором, так как построена как алгебраическая сумма векторов. Другими словами, выражение, которое стоит в фигурных скобках, является тензором четвертого ранга. Этот тензор:
    \begin{displaymath} R^{\alpha}_{\mu \nu \lambda} = {\displaystyle\partial \Gamma... ...mbda} -\Gamma^{\alpha}_{\mu \rho} \Gamma^{\rho}_{\nu \lambda} \end{displaymath} (7.13)

    называется тензором кривизны. Поэтому пространство является эвклидовым, если (7.13) равен нулю в каждой точке этого пространства.

    Произведение двух векторов на которых построен параллелограмм есть площадь этого бесконечно малого параллелограмма.

    7.2.3 Изменение вектора при переносе по замкнутой кривой

    Рассмотрим теперь изменение вектора при параллельном переносе вдоль замкнутой кривой конечного размера. Разобъем ее на бесконечно малые параллелограммы, как показано на рис. 7.2

    Рисунок 7.2: На рисунке изображена замкнутая кривая конечных размеров $L$. Разобъем ее на совокупность бесконечно малых параллелограммов так, чтобы перенос по соседним сторонам параллелограммов проходил в противоположных направлениях. Тогда, как легко видеть, полное изменение вектора при переносе вдоль $L$ складывается из интеграла по площади, стягиваемой этой кривой от произведения тензора кривизны на сам вектор.
    \begin{figure}\centerline{\epsfxsize=0.7\textwidth\epsfbox{fig7_2.ai}}\end{figure}

    Теперь можно получить изменение компонент вектора $A^{\alpha}$ при параллельном перносе вдоль замкнутой кривой конечных размеров в виде интеграла по поверхности, стягиваемой этой кривой:

    \begin{displaymath} \Delta A^{\alpha} = -{1 \over 2} \int dS^{\mu \nu} R^{\alpha}_{\beta \mu \nu } A^{\beta} \end{displaymath}

    7.3 Свойства тензора кривизны

    Свойства тензора кривизны мы уже немного обсудили при анализе второй ковариантной производной от вектора. Обсудим алгебраические свойства тензора кривизны более подробно. Для этого опустим верхний индекс и будем работать только с ковариантным тензором четвертого ранга.

    Из уравнения (7.4) следуют свойства симметрии тензора кривизны:


    $\displaystyle R_{\alpha \beta \mu \nu}= -R_{\beta \alpha \mu \nu}$ (7.14)
    $\displaystyle R_{\alpha \beta \mu \nu}= -R_{\alpha \beta \nu \mu}$ (7.15)
    $\displaystyle R_{\alpha \beta \mu \nu}= R_{\mu \nu \alpha \beta }$ (7.16)
    $\displaystyle R_{\alpha \beta \mu \nu} + R_{\alpha \nu \beta \mu} +R_{\alpha \mu \nu \beta } =0$ (7.17)

    До сих пор мы рассматривали общий случай неэвклидовой геометрии, теперь вспомним, что нам нужено только четырехмерное пространство. В этом случае пары индексов $\alpha \beta$ и $\mu \nu$ пробегают 6 различных наборов значений. Поэтому есть 6 компонент тензора кривизны с одинаковыми и $6 \cdot {\displaystyle 5\over\displaystyle 2}= 15$ компонент с различными значениями индексов. Три компоненты с четырмя различными индексами связаны уравнением (7.17), поэтому всего имеется 20 независимых компонент.

    Существует одно дифференциальное тождество, которое называется тождеством Бьянки:
    \begin{displaymath} R^{\alpha}_{ \beta \mu \nu; \rho} + R^{\alpha}_{ \beta \rho \mu; \nu} + R^{\alpha}_{ \beta \nu \rho; \mu} =0 \end{displaymath} (7.18)

    Из тензора кривизны четвертого ранга образуются дополнительно две величины. Одна является тензором второго ранга и образуется сверткой верхнему и второму нижнему индексам:
    \begin{displaymath} R_{\mu \nu}=R^{\rho}_{. \mu \rho \nu} \end{displaymath} (7.19)

    Тензор Риччи является симметричным тензором, поэтому в четырехмерном пространстве он имеет 10 независимых компонент (как и метрический тензор). Сверткой по оставшимся двум индексам можно получить скалярную величину, которая называется скалярной кривизной пространства:


    \begin{displaymath} R= g^{\mu \nu} R_{\mu \nu} \end{displaymath} (7.20)

    Поскольку (7.20) является скалярной величиной, то она является одновременно инвариантной относительно координатных преобразований и называется также скалярной кривизной пространства.

    Из тождеств Бьянки можно получить важное равенство. Для этого свернем тождество (7.18) по индексам $\alpha \rho$. Тогда получим уравнение вида:

    \begin{displaymath} R^{\alpha}_{\mu \nu \lambda; \alpha} + R_{\nu \lambda; \mu} - R_{\mu \lambda; \nu} =0 \end{displaymath}

    Свернем это уравнение еще раз с метрическим тензором, получим равенство:
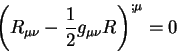    \begin{displaymath} \left( R_{\mu \nu} -{\displaystyle 1\over\displaystyle 2} g_{\mu \nu}R\right)^{;\mu}=0 \end{displaymath} (7.21)

    В этом уравнении четырехмерная дивергенция некоторого тензора второго ранга равна нулю. Этот тензор:
    \begin{displaymath} G_{\mu \nu} = R_{\mu \nu} - {\displaystyle 1\over\displaystyle 2} g_{\mu \nu} R \end{displaymath} (7.22)

    играет важную роль в общей теории относительности. Иногда его называют тензором Эйнштейна.

    7.4 Вариации тензора кривизны

    Рассмотрим теперь изменение символов Кристоффеля, а также тензоров кривизны, Риччи и скалярной кривизны при вариациях метрики. Полученные уравнения мы будем использовать в дальнейшем как для вывода уравнений гравитационного поля, так и для анализа слабого гравитационного поля и слабого гравитационного поля на фоне сильного поля.

    Пусть у нас есть метрика $g_{\alpha \beta}$, на которую наложены небольшие изменения, которые мы будем обозначать $\delta g_{\alpha \beta}$ и которые являются вариациями метрики. Отметим, что эти две величины по отдельности образуют тензора. Тем не менее сейчас мы будем рассматривать как один тензор, который состоит из "фоновой" метрики и малых поправок:
    \begin{displaymath} g_{\alpha \beta} = g^b_{\alpha \beta} + \delta g_{\alpha \beta} \end{displaymath} (7.23)

    Все величины, которые мы будем вычислять ниже, будем вычислять только до первого порядка малости по вариациям, пренебрегая вкладом вариаций более высокой степени.

    Рассмотрим как связаны вариации контравариантных компонент метрического тензора с вариация ковариантных компонент. Контравариантные компоненты метрического тензора удовлетворяют равенству вида:

    \begin{displaymath} g^{\alpha \rho} g_{\beta \rho} =\delta^{\alpha}_{\beta} \end{displaymath}

    Подставляя сюда ковариантный метрический тензор с вариациями $g_{\alpha \beta} +\delta g_{\alpha \beta}$ и конравариантные компоненты $g^{\alpha \beta} +\delta g^{\alpha \beta}$ получаем связь между контравариантными и ковариантными вариациями:
    \begin{displaymath} \delta g^{\alpha \beta}= -g^{\alpha \mu} g^{\beta \nu} \delta g_{\mu \nu} \end{displaymath} (7.24)

    Отсюда видно, что конравариантные вариации отличаются от ковариантных знаком, а индексы поднимаются метрическим тензором, как и у любых других тензоров.

    Для вычисления вариации определителя метрического тензора введем абсолютно антисимметричный единичный тензор четвертого ранга $e^{\alpha \beta \gamma \delta}$ [8]. Так называется тензор, компоненты которого меняют знак при перестановке любых двух индексов, причем отличные от нуля компоненты равны $\pm 1$. Тогда можно записать определитель метрического тензора как:

    \begin{displaymath} g= {\displaystyle 1\over\displaystyle 24} e^{\alpha \beta \g... ... \epsilon} g_{\beta \zeta} g_{\gamma \eta} g_{\delta \theta} \end{displaymath}

    Теперь можно легко вычислить вариации определителя метрического тензора.

    Вариации определителя с точностью до линейных по $\delta g^{\alpha \beta}$ членов есть:

    \begin{displaymath} \delta g= -g^{\alpha \beta} \delta g_{\alpha \beta } \end{displaymath}

    Приведем также одну полезную формулу, содержащую вариации плотности метрического тензора:

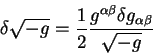
    \begin{displaymath} \delta \sqrt{-g}= {\displaystyle 1\over\displaystyle 2} {\di... ...a \beta} \delta g_{\alpha \beta}\over\displaystyle\sqrt{-g}} \end{displaymath}

    В этих двух уравнениях опущен индекс $b$ в символах фоновой метрики, но поскольку мы договорились оставлять только линейные члены по вариациям, легко определить величины содержащие этот индекс.

    Рассмотрим теперь вариации символов Кристоффеля. Вновь оставляя только линейные члены по $\delta g_{\alpha \beta}$ получаем уравнение для вариаций символов Кристоффеля:
    \begin{displaymath} \delta \Gamma^{\mu}_{\alpha \beta}= {1 \over 2} g^{\mu \nu} ... ...beta})_{; \alpha} - (\delta g_{\alpha \beta})_{; \nu} \rbrace \end{displaymath} (7.25)

    Отметим, что вариации символов Кристоффеля по отношению к "фоновой" метрике $g^b_{\alpha \beta}$ являются тензорами третьего ранга. Ковариантные производные построены с помощью фоновой метрики $g^b_{\alpha \beta}$.

    Вариации тензора Риччи выражаются через ковариантные производные нового тензора - вариации символов Кристоффеля $\delta \Gamma^{\mu}_{\alpha \beta}$:
    \begin{displaymath} \delta R_{\alpha \beta} = \left( \delta \Gamma^{\mu}_{\alpha... ...} - \left( \delta \Gamma^{\mu}_{\alpha \beta} \right)_{; \mu} \end{displaymath} (7.26)

    Это уравнение можно переписать в терминах вариаций метрики, в них оно имеет вид:
    \begin{displaymath} \delta R_{\alpha \beta} = {1 \over 2} g^{\mu \nu}\lbrace \l... ...+ \left( \delta g_{\alpha \beta} \right)_{;\nu ;\mu} \rbrace \end{displaymath} (7.27)

    9. Уравнения гравитационного поля >>

    Разделы

    8. Уравнение движения в общей теории относительности

    Влияние гравитационного поля на движение частиц в ньютоновской механике хорошо изучено. Уравнение движения частицы представляет собой уравнение в левой части которого стоит ускорение пробной частицы умноженное на массу частицы (в данном случае это инертная масса), в правой части уравнения стоит гравитационная сила. Гравитационная сила, в свою очередь, представляет из себя произведение массы пробной частицы (в данном случае - гравитационной массы) на ускорение со стороны тяготеющего тела: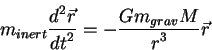

    \begin{displaymath} m_{inert}{\displaystyle d^2 \vec r\over\displaystyle dt^2}= -{\displaystyle Gm_{grav}M\over\displaystyle r^3} \vec r \end{displaymath}

    Поскольку инертная масса тела равна его гравитационной массе (это формулировка принципа эквивалентности, многократно проверенного экспериментально), то движение пробной частицы не зависит от массы этой частицы - перо птицы и кирпич падают в гравитационном поле с одинаковым ускорением (конечно, если пренебречь сопротивлением воздуха).

    В общей теории относительности роль гравитационной силы играет кривизна пространства - времени. Движение в гравитационном поле - это движение в искривленном пространстве, отклонение от движения по прямой линии - это отклонение в движении возникающее в искривленном пространстве времени.

    Вспомним вначале уравнения движения в специальной теории относительности.

    8.1 Уравнение движения пробной частицы в СТО

    В специальной теории относительности уравнение движения пробной частицы имеет вид:
    \begin{displaymath} m_{inert}c^2{\displaystyle d u^{\alpha}\over\displaystyle ds}=F^{\alpha}, \end{displaymath} (8.1)

    где $u^{\alpha}$ - 4$^x$ скорость частицы (физическое определение) или вектор, касательный к траектории частицы (математическое определение). Отметим, что $u^{\alpha}$ - величина безразмерная, а $d s$ имеет размерность [см]. Другими словами, слева стоит величина, которая имеет размерность силы г $\cdot{\displaystyle\mbox{см}\over\displaystyle\mbox{сек}^2}$.

    Уравнения движения электрона в электромагнитном поле имеют вид:
    \begin{displaymath} m_e c^2 {\displaystyle d u^{\alpha}\over\displaystyle ds}=e F^{\alpha \beta} u_{\beta} \end{displaymath} (8.2)

    Сила, которая стоит в левой части уравнения является 4$^x$ инвариантной силой Лоренца, построенной из тензора Максвелла $F^{\alpha \beta}$.

    В случае, когда действующие силы равны нулю $F^{\alpha}=0$, то движение частицы происходит по инерции. Тогда решение уравнения 8.1 имеет тривиальный вид:
    $\displaystyle u^{\alpha}(s)= u^{\alpha}_0$ (8.3)
    $\displaystyle x^{\alpha}(s) = u^{\alpha} \cdot s +x^{\alpha}_0$ (8.4)

    Движение по инерции - это движение по прямой линии. Прямая линия является линией кратчайшей длины между двумя точками в эвклидовой и псевдоэвклидовой геометрии. В неэвклидовой геометрии линия кратчайшей длины называется геодезической линией. Движение в случае, когда внешние силы равны нулю, в неэвклидовой геометрии заменяется общековариантным уравнением - движением по геодезической линии.

    Отметим также, что решение (8.3) описывает также движение фотона, если полагать, что $u^{\alpha}$ - единичный вектор в направлении распространения фотона, а $s$ - афинный параметр вдоль траектории.

    8.2 Уравнение движения пробной частицы в ОТО

    Движение по геодезической линии описывает движение пробной частицы в гравитационном поле. Это движение является аналогом движения по инерции в пространстве с эвклидовой метрикой.

    Выпишем уравнение движения в общей теории относительности, просто написав ковариантное обобщение уравнения 8.1:
    \begin{displaymath} m_{inert}c^2{\displaystyle D u^{\mu}\over\displaystyle ds}=F^{\mu} \end{displaymath} (8.5)

    Здесь $D$, как мы договорились выше, являются обозначением ковариантного дифференциала. Поэтому уравнения движения в общей теории относительности можно написать более детально в виде:
    \begin{displaymath} m_{inert}c^2{\displaystyle d u^{\mu}\over\displaystyle ds} +... ...c^2 \Gamma^{\mu}_{\alpha \beta} u^{\alpha} u^{\beta}=F^{\mu} \end{displaymath} (8.6)

    Заметим, что теперь уравнения движения являются нелинейными (по скоростям), второй член в левой части уравнений содержит квадратичные произведения скоростей.

    Теперь уравнения движения, например, электрона в электромагнитном поле имеют вид:
    \begin{displaymath} m_e c^2 {\displaystyle D u^{\alpha}\over\displaystyle ds}=e F^{\alpha \beta} u_{\beta} \end{displaymath} (8.7)

    Здесь $F^{\alpha \beta}$ - тензор электромагнитного поля, а $m_e$ и $e$ масса и заряд электрона соответственно.

    Отметим, что теперь движение пробной частицы в отсутствии внешних сил $F^{\alpha}=0$ уже не является движением по прямым линиям, как это было в эвклидовой геометрии (8.3). Движение в отсутствии внешних сил представляет из себя систему дифференциальных уравнений второго порядка для всех четырех координат, которые описывают четырехмерную траекторию пробной частицы.

    8.2.1 Уравнения движения в трехмерном виде

    Рассмотрим уравнения движения пробных частиц, написанные в трехмерном виде. Будем считать, что частица является нерелятивистской (т.е. интервал между двумя событиями: выходом частицы из точки $A$ и появление частицы в точке $B$ не равен нулю). Уравнения движения пробных частиц - уравнения геодезических линий имеют вид (8.6). В качестве афинного параметра вдоль геодезической возмем $s$ - интервал между событиями (т.к. он не равен нулю). Кроме того, напомним, что 4$^x$ скорость - это единичный вектор касательный к траектории движения, по определению:

    \begin{displaymath} u^{\alpha}={\displaystyle d x^{\alpha}\over\displaystyle d s} \end{displaymath}

    Это значит, что уравнения движения можно переписать в виде, который содержит ускорения (вторую производную от координаты частицы по афинному параметру):
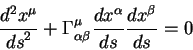    \begin{displaymath} {\displaystyle d^2 x^{\mu}\over\displaystyle ds^2} + \Gamma^... ...style ds} {\displaystyle d x^{\beta}\over\displaystyle d s}= 0 \end{displaymath} (8.8)

    Преобразуем вторую производную от координаты с пространственным индексом $x^i$ по интервалу к второй производной по координате с нулевым индексом:


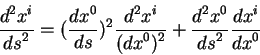
    \begin{displaymath} {\displaystyle d^2 x^i\over\displaystyle d s^2}=({\displayst... ...splaystyle ds^2} {\displaystyle d x^i\over\displaystyle d x^0} \end{displaymath}

    Здесь ${\displaystyle d x^0\over\displaystyle d s}$ - нулевая компонента 4$^x$ скорости, а $ {\displaystyle d^2 x^0\over\displaystyle ds^2} $ - 4$^x$ мерное уравнение движения с индексом 0.

    Это уравнение можно обратить, получая уравнения для ускорений пробной частицы в виде:

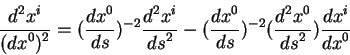
    \begin{displaymath} {\displaystyle d^2 x^i\over\displaystyle(d x^0)^2} = ({\disp... ...ystyle d s^2}) {\displaystyle d x^i\over\displaystyle d x^0} \end{displaymath}

    Подставим в это уравнение выражение для

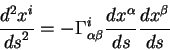
    \begin{displaymath} {\displaystyle d^2 x^i\over\displaystyle d s^2} = - \Gamma^i... ...style d s} {\displaystyle d x^{\beta}\over\displaystyle d s} \end{displaymath}

    и


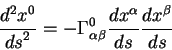
    \begin{displaymath} {\displaystyle d^2 x^0\over\displaystyle d s^2} = - \Gamma^0... ...style d s} {\displaystyle d x^{\beta}\over\displaystyle d s} \end{displaymath}

    После завершения всех выкладок, окончательно получаем уравнение движения в виде:

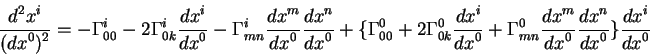
    \begin{displaymath} {\displaystyle d^2 x^i\over\displaystyle(d x^0)^2} = -\Gamma... ...e d x^0}\rbrace {\displaystyle d x^i\over\displaystyle d x^0} \end{displaymath}

    До сих пор дифференцирование проводилось по координате с нулевым индексом, поскольку эта координата имеет такую же размерность как и остальные координаты [см]. Однако, для получения обычного трехмерного уравнения движения необходимо перейти к дифференцированию по времени $x^0=ct$. Умножим обе части полученного уравнения на квадрат скорости света и получим уравнение движения в обычном трехмерном виде:
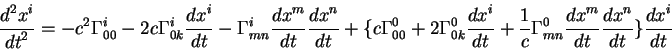    \begin{displaymath} {\displaystyle d^2 x^i\over\displaystyle d t^2} = -c^2 \Gamm... ...tyle d t} \rbrace {\displaystyle d x^i\over\displaystyle d t} \end{displaymath} (8.9)

    Сравнивая обычное уравнение движения в ньютоновской гравитации:

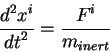
    \begin{displaymath} {\displaystyle d^2 x^i\over\displaystyle d t^2}= {\displaystyle F^i\over\displaystyle m_{inert}} \end{displaymath}

    можно сделать вывод о том, что аналогом ньютоновской силы является член вида:

    \begin{displaymath} F^i_{grav}= - m_{grav} c^2 \Gamma^i_{00} \end{displaymath}

    Из приведенного уравнения видно, что (8.9) содержит члены разных порядков по отношению характерной скорости движения пробной частицы к скорости света. Самый большой член - сила Ньютона, но существуют и более слабые силы, которые, тем не менее вносят вклад в движение частицы в гравитационном поле. Они называются постньютоновскими поправками.

    Более полный анализ уравнений движения, в частности вклада постньютоновских поправок мы проделаем позже.

    8.3 Девиация геодезический линий

    Девиацией двух бесконечно близких геодезических линий называется отклонение этих линий между собой.

    Рассмотрим две бесконечно близкие геодезические линии. Одна линия характеризуется несколькими параметрами. Выберем два из них. Один параметр назовем $\lambda$, он будет афинным параметром вдоль линии. Второй параметр выберем так, чтобы он отсчитывался вдоль направления вектора, который соединяет две указанные геодезические линии и является перпендикулярным вектору, касательному первой геодезической линии. Этот параметр назовем $\eta$. Теперь уравнение геодезической являетмя функцией двух параметров $x^{\alpha}(\lambda, \eta)$. Первый параметр $\lambda$ отчитывает длину вдоль геодезической, второй параметр $\eta$ отсчитывает "номер" геодезической линии, координату в перпендикулярном направлении.

    Вектор касательный к траектории геодезической линии, как прежде будем обозначать $u^{\alpha}$. Введем второй вектор $v^{\alpha}$, который будет касательным к линии, соединяющие две геодезические. Отметим полезное равенство:

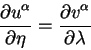
    \begin{displaymath} {\displaystyle\partial u^{\alpha}\over\displaystyle\partial ... ...ystyle\partial v^{\alpha}\over\displaystyle\partial \lambda} \end{displaymath}

    Докажем еще одно равенство, важное для наших рассуждений. Рассмотрим ковариантную производную от вектора $v^{\alpha}$ вдоль геодезической:

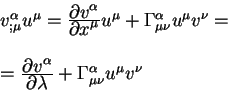
    \begin{displaymath} \begin{array}{l} v^{\alpha}_{; \mu} u^{\mu}= {\displaystyle\... ...ambda} + \Gamma^{\alpha}_{\mu \nu} u^{\mu} v^{\nu} \end{array}\end{displaymath}

    Спомним теперь, что вектор 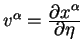$v^{\alpha}={\displaystyle\partial x^{\alpha}\over\displaystyle\partial \eta}$. Поскольку можно поменять частные производные местами, то производную от вектора $v^{\alpha}$ по параметру $\lambda$ можно записать, как производную от вектора $u^{\alpha}$ по параметру $\eta$. Поэтому можно продолжить верхнее равенство как:

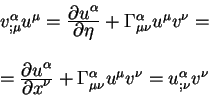
    \begin{displaymath} \begin{array}{l} v^{\alpha}_{; \mu} u^{\mu}={\displaystyle\p... ...u \nu} u^{\mu} v^{\nu} =u^{\alpha}_{;\nu}v^{\nu} \end{array} \end{displaymath}

    Теперь выпишем само равенство, которое было доказано:
    \begin{displaymath} v^{\alpha}_{; \mu} u^{\mu} = u^{\alpha}_{; \mu} v^{\mu} \end{displaymath} (8.10)

    Рассмотрим теперь как меняется вектор $v^{\alpha}$ вдоль геодезической линии. Поскольку длина этого вектора является расстояние между геодезическими, то сам вектор показывает как меняется расстояние и ориентация двух пробных частиц, которые движутся по геодезическим линиям в гравитационном поле. В обычной ньютоновской теории тяготения, изменение расстояния между пробными частицами вызывается приливными силами. Найдем аналог приливных сил в ньютоновской механики в общей теории относительности.

    Для этого рассмотрим вначале первую ковариантную производную от вектора $v^{\alpha}$ вдоль геодезической:

    \begin{displaymath} {\displaystyle Dv^{\alpha}\over\displaystyle d \lambda} = v^{\alpha}_{;\gamma}u^{\gamma} \end{displaymath}

    Поскольку производная по параметру $\lambda$ может быть выражена как производные по координатам, умноженные на вектор вдоль геодезической. Точно так же можно выразит и вторую производную.

    Рассмотрим теперь вторую производную от вектора $v^{\alpha}$ вдоль геодезической:

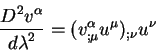
    \begin{displaymath} {\displaystyle D^2 v^{\alpha}\over\displaystyle d \lambda^2} = (v^{\alpha}_{;\mu}u^{\mu})_{; \nu} u^{\nu} \end{displaymath}

    В этом равенстве прием перехода от дифференцирования по афинному параметру к дифференцированию по координатам применен дважды. Воспользуемся также равенством (8.10) и выразим величину в круглых скобках через производную от вектора касательного к геодезической, тогда получим:

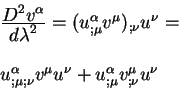
    \begin{displaymath} \begin{array}{l} {\displaystyle D^2 v^{\alpha}\over\displays... ...u^{\nu} + u^{\alpha}_{;\mu}v^{\mu}_{; \nu} u^{\nu} \end{array}\end{displaymath}

    В первом члене меняем порядок ковариантного дифференцирования:

    \begin{displaymath} u^{\alpha}_{;\mu ; \nu} = u^{\alpha}_{;\nu ; \mu} - R^{\alpha}_{\rho \mu \nu} u^{\rho}, \end{displaymath}

    а ко второму вновь применяем равенство (8.10). Получаем, что вторая ковариантная производная от вектора $v^{\alpha}$ есть:

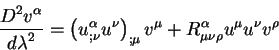
    \begin{displaymath} {\displaystyle D^2 v^{\alpha}\over\displaystyle d \lambda^2}... ...v^{\mu} + R^{\alpha}_{\mu \nu \rho} u^{\mu} u^{\nu} v^{\rho} \end{displaymath}

    Обратим внимание на то, что в тензоре кривизны изменен порядок индексов, поэтому и знак перед тензором поменялся. Первый член равен нулюб в силу уравнения геодезической линии (см. (6.17)).

    Поэтому окончательно вторая ковариантная производная от вектора $v^{\alpha}$ равна:
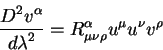    \begin{displaymath} {\displaystyle D^2 v^{\alpha}\over\displaystyle d \lambda^2} = R^{\alpha}_{\mu \nu \rho} u^{\mu} u^{\nu} v^{\rho} \end{displaymath} (8.11)

    Умножая это уравнение на величину $\Delta \eta$ - расстояние между геодезическими получаем уравнение для вектора, который соединяет две пробные частиц, которые свободно движутся по двум близким геодезическим линиям.

    Это уравнение называется уравнение девиации близких геодезических линий.


    << 7. Тензор кривизны | Оглавление | 9. Уравнения гравитационного поля >>

    Рекомендуемая и цитируемая литература >>

    Разделы

    9. Уравнения гравитационного поля

    Уравнение гравитационного поля в ньютоновской механике хорошо известно. Гравитационная сила, действующая со стороны точечной массы $M$ на пробную частицу массы $m$, расположенную на расстоянии $R$ от этого тела, представляется как:

    \begin{displaymath} \vec F = -{\displaystyle G m M\over\displaystyle R^3} \vec R \end{displaymath}

    Гравитационную силу от произвольного распределения масс можно получить взяв интеграл по плотности. Однако, чаще в теоретической физике вводят понятие гравитационного потенциала $\phi$, с помощью которого уже вычисляют гравитационную силу действующую на пробную частицу:

    \begin{displaymath} F^i = - m_{grav} {\displaystyle\partial \phi\over\displaystyle\partial x^i} \end{displaymath}

    Гравитационный потенциал создается распределением масс и уравнение для потенциала имеет вид уравнения типа скалярного поля. В отличие от современных уравнений скалярного поля, уравнения ньютоновского гравитационного поля не являются релятивистски инвариантными, поскольку гравитационная теория Ньютона существенно нерелятивистская теория. Поэтому уравнения поля есть уравнение типа Пуассона:
    \begin{displaymath} \bigtriangleup \phi = 4 \pi G \rho \end{displaymath} (9.1)

    Естественно, что ньютоновские уравнения гравитационного поля не могли быть согласованы с принципами релятивистской физики. Потребовалось создание новой теории гравитации - общей теории относительности.

    9.1 Создание уравнений общей теории относительности

    После создания специальной теории относительности А.Эйнштейн начал разработку идей связанных с распространением принципа относительности на ускоренные системы отсчета. Достаточно скоро стало понятно, что невозможно распространение принципа относительности на ускоренные системы отсчета без обсуждения гравитационного поля.

    Первая статья [15] относится лишь к однородноускоренным системам координат. Однако уже там появляется идея - отождествление ускорения и однородного гравитационного поля. Эта идея оказалась очень плодотворной и решающей для обобщения принципа относительности - создания общей теории относительности, которая включает в себя теорию релятивистского гравитационного поля. Там же (параграф 19 этой статьи) А.Эйнштейн получает связь между темпом течения времени в гравитационном поле с различным потенциалом:

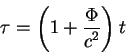
    \begin{displaymath} \tau =\left( 1 + {\displaystyle\Phi\over\displaystyle c^2}\right) t \end{displaymath}

    В следущем параграфе А.Эйнштейн делает вывод о том, что гравитационное поле надо, по - видимому, характеризовать переменной скоростью света:

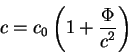
    \begin{displaymath} c=c_0 \left( 1 + {\displaystyle\Phi\over\displaystyle c^2}\right) \end{displaymath}

    Следущую важную работу, посвященную гравитации, А.Эйнштейн опубликовал только в 1912 г [16]. В ней он полемизирует с Абрагамом, который построил свою теорию гравитации и строит теорию гравитации для случая статического гравитационного поля. В этой статье все еще эксплуатируется идея переменности скорости света. А.Эйнштейн ищет уравнение для случая статического гравитационного поля, при этом руководствуется уравнением нерелятивистского гравитационного поля. Он приходит к выводу, что уравнение должно быть однородно по скорости света и приводит его в виде:

    \begin{displaymath} \Delta c =k c \rho \end{displaymath}

    В следущей статье, опубликованной в том же 1912 году А.Эйнштейн учитывает вклад энергии самого гравитационного поля в гравитационное поле и впервые получает нелинейное уравнение вида:

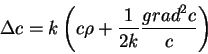
    \begin{displaymath} \Delta c =k \left(c \rho +{\displaystyle 1\over\displaystyle 2k} {\displaystyle grad^2 c\over\displaystyle c}\right) \end{displaymath}

    Уравнения гравитационного поля становятся нелинейными.

    В следущем 1913 г. А.Эйнштейн в совместной статье с М.Гроссманом [17] ясно формулирует связь гравитационного поля с метрическим тензором $g_{\mu \nu}$. Таким образом тензор второго ранга становится величиной, которая описывает гравитационное поле. В этой же статье окончательно появляется идея тождественности искривленного пространства - времени и гравитации, появляется тензор кривизны и другие величины свойственные для неэвклидовой геометрии. Там же делается попытка вывести релятивистские уравнения гравитационного поля.

    Окончательно релятивистские уравнения гравитационного поля были выведены в 1916 г. В статье, опубликованной в "Анналах физики" [18], А.Эйнштейн сформулировал общую теорию относительности, придал окончательный вид уравнениям гравитационного поля, которыми мы пользуемся по сей день (а также ввел знаменитое правило суммирования по повторяющимся индексам).

    Весьма скоро после начала работы над общей теорией относительности, А.Эйнштейн понял значение гамильтонова подхода для вывода уравнений поля. Этот подход оказался очень плодотворным в современной теоретической физике. Он связан с понятием экстремума действия и принципом наименьшего действия. Именно таким образом мы и будем выводить уравнения гравитационного поля.

    9.1.1 Может ли скалярное поле описывать гравитацию?

    Уравнение (9.1) является существенно нерелятивистским урапвнением. Это легко показать. Решением уравнения (9.1) является интеграл:

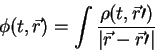
    \begin{displaymath} \phi (t, \vec r) = \int {\displaystyle\rho(t, \vec r \prime)\over\displaystyle\vert\vec r -\vec r \prime\vert} \end{displaymath}

    любые изменения в источнике ($\rho$ зависит от времени) могут быть мгновенно обнаружены (здесь мы опускаем проблемы связанные с обнаружением сигнала) в тот же момент времени и на любом расстоянии от источника. Это прямо противоречит постулату о невозможности передачи информации со скоростью превышающей скорость света.

    Изменить это уравнение на релятивистское крайне просто. Необходимо добавить вторую производную по времени, превратив уравнение Пуассона в уравнение д'Аламбера:
    \begin{displaymath} \Box \phi = 4 \pi G \rho \end{displaymath} (9.2)

    Слева в уравнении теперь стоит релятивистски инвариантный оператор, который обеспечивает релятивистскую инвариантность. Справа должен стоять источник поля (плотность), обладающий такими же свойствами как и поле. Если поле описывается скалярной величиной, то и источник поля также должен быть скалярной величиной. Если гравитационное поле описывается тензором ранга $n$, то и источник должен быть тензором ранга $n$.

    Поскольку одноименные заряды в гравитации притягиваются ( в отличие от электромагнитной теории, в которой одноименные заряды отталкиваются ), то гравитационное поле должно описываться тензором четного ранга - скалярным полем, полем тензора второго ранга и т.п. 9.1

    Поэтому при релятивистском обобщении ньютоновской теории гравитации, определяемой уравнением (9.2), необходимо определить тензорные свойства источника поля. Величина $\rho$ может быть нерелятивистским пределом либо тензора энергии - импульса $T_{\mu \nu}$, либо скалярной величины - следа этого тензора $T^{\mu}_{\mu}$. В первом случае гравитационное поле представляется тензором второго ранга, во втором случае - тензором первого ранга. Эксперимент показывает, что справедлива теория гравитации с полем второго ранга в качестве полевой переменной.

    9.2 Вывод уравнений поля из вариационного принципа

    9.2.1 Действие для гравитационного поля

    Итак мы должны найти связь между метрическим тензором $g_{\mu \nu}$ и распределением масс, которая заменит уравнение (9.1) классической ньютоновской теории тяготения. Рассмотрим вывод уравнений гравитационного поля в общей теории относительности ( уравнений Эйнштейна ) используя принцип наименьшего действия. Уравнения гравитационного поля получатся вариацией действия по метрическому тензору - полевой переменной. Это действие, как и для полей другого вида должно быть представлено в виде некоторого скаляра, который является интегралом по 4$^x$ пространству от некоторой скалярной плотности, зависящей от метрического тензора и первых производных метрического тензора. Такой скалярной плотностью является только величина:

    \begin{displaymath} \sqrt{-g} R \end{displaymath}

    образуемая из скаляра кривизны. Действие $S_g$ гравитационного поля можно, следовательно, представить в виде:
    \begin{displaymath} S_g= - \kappa \int R \sqrt{-g} \; d^4 x \end{displaymath} (9.3)

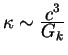    Здесь $\kappa$ -некоторая новая гравитационная постоянная. Определить ее связь с кавендишевой гравитационной постоянной с точностью до безразмерного постоянного множителя достаточно просто - действие имеет размерность энергии, скаляр кривизны имеет размерность см$^{-2}$, а объем при интегрировании см$^4$. Отсюда из соображений размерности находим, что $\kappa \sim {\displaystyle c^3\over\displaystyle G_k}$, где $G_k$ - гравитационная постоянная Кавендиша.

    Скалярная кривизна наряду с метрическим тензором и его первыми производными содержит также и вторые производные от метрического тензора. Применяя к $\sqrt{-g} R$ производную Эйлера - Лагранжа можно получить уравнеия гравитационного поля. Прямые вычисления очень трудоемкие и содержат большое количество выкладок. Мы несколько упростим вычисления, для чего воспользуемся двумя свойствами скаляра кривизны.

    Первый прием при выводе уравнений гравитационного поля впервые применили [8]. Он основан на том, что в скалярной кривизне вторые производные метрического тензора входят линейно, что позволяет выделить полную дивергенцию, которая не влияет на уравнения движения. Поэтому действие $S_g$ можно представить в виде:

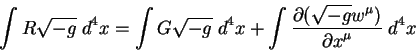
    \begin{displaymath} \int R \sqrt{-g} \; d^4 x = \int G \sqrt{-g} \; d^4 x + \int... ...sqrt{-g} w^{\mu})\over\displaystyle\partial x^{\mu}} \; d^4 x \end{displaymath}

    Слева стоит скалярная величина9.2. Справа стоят два неинвариантных члена. Хотя их сумма является инвариантом, каждый из членов неинвариантен. Для вывода уравнений поля нарушение инвариантности не страшно, поскольку при выводе используются вариации этих величин. Напомним, что вариации многих неинвариантных величин являются уже инвариантными, пример, символ Кристоффеля не являются тензором, в то время как вариации символа уже являются тензором третьего ранга.

    Кроме того, полную дивергенцию по теореме Остраградского можно преобразовать в интеграл по трехмерной гиперповерхности. При вычислении вариаций этот член будет равен нулю, так как по определению вариации на гиперповерхности, охватывающей объем равны нулю. Поэтому вариация гравитационного действия равна:

    \begin{displaymath} \delta S_g = -\kappa \delta \int G \sqrt{-g} \; d^4 x \end{displaymath}

    Найдем величину $G$, которая определяет действие гравитационного поля и вычислим ее вариацию относительно метрического тензора.

    Скалярная плотность кривизны выражается через метрический тензор и символы Кристоффеля как:

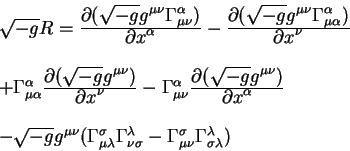
    \begin{displaymath} \begin{array}{l} \sqrt{-g} R = {\displaystyle\partial (\sqrt... ..._{\mu \nu} \Gamma^{\lambda}_{\sigma \lambda}\bigr) \end{array}\end{displaymath}

    Находим величины

    \begin{displaymath} w^{\alpha} = g^{\mu \nu} \Gamma^{\alpha}_{\mu \nu} - g^{\mu \alpha} \Gamma^{\nu}_{\mu \nu} \end{displaymath}

    и


    \begin{displaymath} G=g^{\mu \nu}\bigl( \Gamma^{\sigma}_{\mu \lambda} \Gamma^{\... ...ma^{\sigma}_{\mu \nu} \Gamma^{\lambda}_{\sigma \lambda}\bigr) \end{displaymath}

    Производная Эйлера - Лагранжа величины $\sqrt{-g}G$ определяет уравнения гравитационного поля.

    9.2.2 Производная Эйлера - Лагранжа от действия и уравнения гравитационного поля в вакууме

    Производная Эйлера - Лагранжа от величины $\sqrt{-g}G$ определяется как:

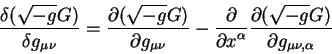
    \begin{displaymath} {\displaystyle\delta (\sqrt{-g}G)\over\displaystyle\delta g_... ... (\sqrt{-g}G)\over\displaystyle\partial g_{\mu \nu, \alpha}} \end{displaymath}

    Как видно из определения, $\sqrt{-g}G$ зависит от самого метрического тензора $g_{\mu \nu}$ и символов Кристоффеля. Вычислим частные производные от $g^{\mu \nu}$ и $\sqrt{-g}$ по метрическому тензору $g_{\mu \nu}$.

    Для вычисления частных производных от контравариантного метрического тензора $g^{\mu \nu}$ по ковариантному метрическому тензору $g_{\mu \nu}$ воспользуемся равенством вида:

    \begin{displaymath} g^{\alpha \gamma} g_{\gamma \beta} = \delta^{\alpha}_{\beta} \end{displaymath}

    беря частную производную по ковариантному метрическому тензору по частям получаем уравнение вида:

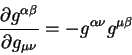
    \begin{displaymath} {\displaystyle\partial g^{\alpha \beta}\over\displaystyle\partial g_{\mu \nu}} = -g^{\alpha \nu} g^{\mu \beta} \end{displaymath}

    в этом уравнении достаточно трудно усмотреть симметрию по паре индексов $\alpha \beta$ и $\mu \nu$. Для того, чтобы сделать эту симметрию явной, образуем симметричную сумму в правой части этого равенства, тогда частная производная будет равна:

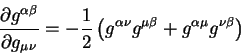
    \begin{displaymath} {\displaystyle\partial g^{\alpha \beta}\over\displaystyle\pa... ...alpha \nu} g^{\mu \beta} +g^{\alpha \mu} g^{\nu \beta} \right) \end{displaymath}

    Для вычисления частной производной от корня из детерминанта $\sqrt{-g}$ воспользуемся равенством:

    \begin{displaymath} d(-g) = (-g) g^{\mu \nu} dg_{\mu \nu} \end{displaymath}

    тогда получаем

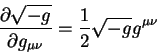
    \begin{displaymath} {\displaystyle\partial \sqrt{-g}\over\displaystyle\partial g_{\mu \nu}} = {1 \over 2} \sqrt{-g} g^{\mu \nu} \end{displaymath}

    Частные производные от плотности действия $\sqrt{-g}G$ по ковариантному метрическому тензору $g_{\mu \nu}$ формируются только из частных производных от контраваиантных компонент метрического тензора $g^{\mu \nu}$, которые входят в символы Кристоффеля и в определитель $\sqrt{-g}$. Производные от символа Кристоффеля есть:

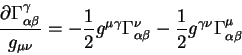
    \begin{displaymath} {\displaystyle\partial \Gamma^{\gamma}_{\alpha \beta}\over\d... ... \beta} -{1 \over 2}g^{\gamma \nu} \Gamma^{\mu}_{\alpha \beta} \end{displaymath}

    Выпишем теперь частную производную от плотности гравитационного действия $\sqrt{-g}G$ по метрическому тензору:

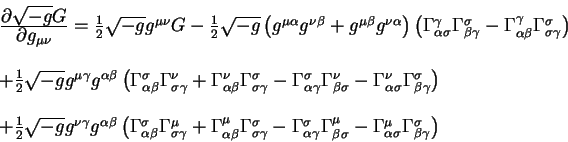
    \begin{displaymath} \begin{array}{l} {\displaystyle\partial \sqrt{-g}G\over\disp... ...a \sigma} \Gamma^{\sigma}_{\beta \gamma} \right) \end{array} \end{displaymath}

    Несмотря на громоздкий вид структура этой формулы достаточна простая.

    Более сложной является структура частной производной от гравитационного действия по производной от метрического тензора. Рассмотрим теперь ее.

    Рассмотрим как происходит дифференцирование функции $\sqrt{-g}G$ по производной метрического тензора, скажем, $g_{i k , l}$. Поскольку производные от метрического тензора по координатам содержатся только в символах Кристоффеля $\Gamma^{\alpha}_{\mu \nu}$, то и частная производная будет действовать только на эти члены. Только для этих вычислений будем использовать латинские индексы в обозначениях метрического тензора. Только в этом параграфе будем считать, что они пробегают значения 0, 1, 2, 3.

    Выпишем частную производную от символов Кристоффеля по нашей динамической переменной - частной производной от метрического тензора по одной из координат:

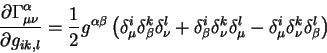
    \begin{displaymath} {\displaystyle\partial \Gamma^{\alpha}_{\mu \nu}\over\displa... ...mu} - \delta^i_{\mu} \delta^k_{\nu} \delta^l_{\beta} \right) \end{displaymath}

    Подставим эту формулу в выражение для частной производной от плотности гравитационного действия по нашей динамической переменной - частной производной от метрического тензора по одной из координат

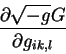
    \begin{displaymath} {\displaystyle\partial \sqrt{-g} G\over\displaystyle\partial g_{ik,l}} \end{displaymath}

    получим некоторое громоздкое выражение. Не выписывая его здесь целиком, свернем по мертвым индексам суммирования, что значительно упростит запись:

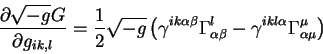
    \begin{displaymath} {\displaystyle\partial \sqrt{-g} G\over\displaystyle\partial... ...a} - \gamma^{ikl \alpha } \Gamma^{\mu}_{\alpha \mu} \right) \end{displaymath}

    В этом уравнении введен новый тензор четвертого ранга

    \begin{displaymath} \gamma^{ik \alpha \beta} =\left( g^{i \alpha} g^{k \beta} + g^{i \beta} g^{k \alpha} - g^{\alpha \beta} g^{ik} \right) \end{displaymath}

    В производную Эйлера - Лагранжа член вида

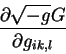
    \begin{displaymath} {\displaystyle\partial \sqrt{-g} G\over\displaystyle\partial g_{ik,l}} \end{displaymath}

    входит не самостоятельно, в от него вычисляется частная производная по координате, которая стоит в динамической переменной - частной производной от метрического тензора по координате

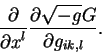
    \begin{displaymath} {\displaystyle\partial\over\displaystyle\partial x^l} {\disp... ...tyle\partial \sqrt{-g} G\over\displaystyle\partial g_{ik,l}}. \end{displaymath}

    После вычисления частных производных по координате $x^l$ появляются производные от символов Кристоффеля по координатам:

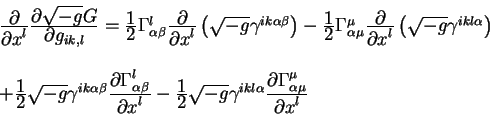
    \begin{displaymath} \begin{array}{l} {\displaystyle\partial\over\displaystyle\pa... ...\mu}_{\alpha \mu}\over\displaystyle\partial x^l} \end{array} \end{displaymath}

    Частные производные от символов Кристоффеля входят в тензор кривизны. Этот тензор имеет ранг 4. Но производные, которые появлись в приведенной выше формуле входят в тензор Риччи. Запишем эту формулу через тензор Риччи $R_{\alpha \beta}$.

    Выражая частные производные от символов Кристоффеля через тензор Риччи получим член в левой части равенства вида:

    \begin{displaymath} {\displaystyle 1\over\displaystyle 2} \sqrt{-g} \gamma^{i k \alpha \beta} R_{\alpha \beta} \end{displaymath}

    Выражая тензор $\gamma^{i k \alpha \beta}$ в виде произведений метрического тензора и свертывая по индексам суммирования получаем член вида:

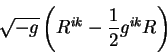
    \begin{displaymath} \sqrt{-g} \left( R^{i k} - {\displaystyle 1\over\displaystyle 2} g^{i k} R \right) \end{displaymath}

    Оставшиеся четыре члена представляют произведения символов Кристоффеля, окончательно выпишем производную от гравитационного действия в виде:

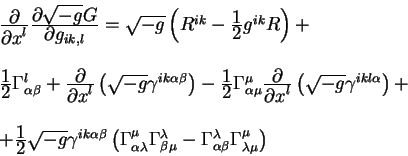
    \begin{displaymath} \begin{array}{l} {\displaystyle\partial\over\displaystyle\pa... ...\alpha \beta} \Gamma^{\mu}_{\lambda \mu} \right) \end{array} \end{displaymath}

    Выпишем окончательно производную Эйлера - Лагранжа от плотности гравитационного действия:

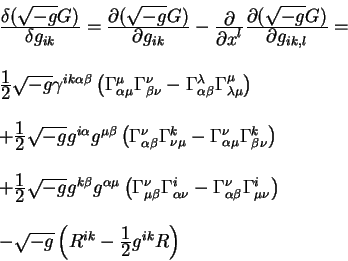
    \begin{displaymath} \begin{array}{l} {\displaystyle\delta (\sqrt{-g} G)\over\dis... ...playstyle 1\over\displaystyle 2} g^{i k} R \right) \end{array}\end{displaymath}

    Для упрощения дальнейших выкладок выберем систему координат, в которой удовлетворяется условие $\sqrt{-g}=1$ во всем пространстве - времени. Поскольку это только одно условие, то его можно удовлетворить подходящим выбором системы координат всегда. Доказательство этого утверждения не входит в наш курс. Следствием этого выбора является уравнение:

    \begin{displaymath} \Gamma^{\mu}_{\alpha \mu} =0 \end{displaymath}

    справедливое для любого значения индекса $\alpha$. Тогда первый член в этом уравнении обращается в нуль.

    Подставим уравнение для производной Эйлера - Лагранжа в вариацию действия:

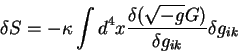
    \begin{displaymath} \delta S= -\kappa \int d^4 x {\displaystyle\delta (\sqrt{-g}G)\over\displaystyle\delta g_{ik}} \delta g_{ik} \end{displaymath}

    Свертка второго и третьего членов с вариацией метрического тензора $\delta g_{ik}$ дает нуль, поскольку это сумма второго и третьего членов антисимметрична по индексам $i\; k$. В результате вариация гравитационного действия по метрическому тензору равна:

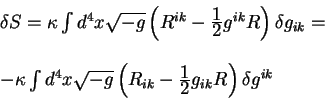
    \begin{displaymath} \begin{array}{l} \delta S= \kappa \int d^4 x \sqrt{-g} \left... ...er\displaystyle 2} g_{i k} R \right) \delta g^{ik} \end{array}\end{displaymath}

    Заметим, что знак минус в последнем равенстве появляется, поскольку вариации контравариантных компонент метрического тензора противоположна вариациям ковариантных компонент:

    \begin{displaymath} \delta g^{\alpha \beta} = -{1 \over 2} \left( g^{i \alpha} g^{k \beta} +g^{k \alpha} g^{i \beta} \right) \delta g_{i k} \end{displaymath}

    Из вариации действия гравитационного поля сразу можно получить релятивистские уравнения поля в пустом пространстве:
    \begin{displaymath} R_{\alpha \beta} - {\displaystyle 1\over\displaystyle 2} g_{\alpha \beta} R =0 \end{displaymath} (9.4)

    Это уравнение эквивалентно уравнению:

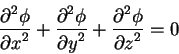
    \begin{displaymath} {\displaystyle\partial^2 \phi\over\displaystyle\partial x^2}... ...isplaystyle\partial^2 \phi\over\displaystyle\partial z^2} = 0 \end{displaymath}

    в ньютоновской теории гравитационного поля.

    Вариация гравитационного действия вычислена в определенной системе координат, которая удовлетворяет условию $\sqrt{-g}=1$. Однако, уравнения гравитационного поля получены в общековариантном виде, который справедлив независимо от выбора системы координат.

    Для вывода релятивистских уравнений, которые связывают гравитационное поле и распределение материи необходимо найти величину, которая получается при вариации плотности действия от материи по метрическому тензору.

    9.2.3 Вывод уравнений гравитационного поля методом Паллатини

    Прежде чем перейти в выводу уравнений общей теории относительности, которые связывают распределение гравитационного поля (метрического тензора) с распределением материи приведем еще один вывод вариации действия гравитационного поля, который является общековариантным и не требует привлечения специальной системы координат. При этом, вывод уравнений релятивистской гравитации методом Паллатини является экономным с точки зрения выкладок.

    Уже в предыдущем параграфе читатель мог обратить внимание на то, что вывод уравнений гравитационного поля был отягощен многими предположениями, в частности о выборе специальной системы координат. Это - необходимое следствие общей ковариантности теории. Если в теории, например, электромагнитного поля, вычисление амплитуд потенциала и их производных по времени и координатам достаточно, чтобы полностью определить эволюцию поля, то в общей теории относительности изменить значения метрического тензора и его производных можно с помощью координатного преобразования. Координатное преобразование метрического тензора не несет никакой физической нагрузки, оно целиком зависит от соображений удобства вычислений. Поэтому необходимо выделить ту часть в метрическом тензоре, которая обуславливает динамическую эволюцию.

    Эта проблема возникла потому, что в метрическим тензоре содержатся дополнительные степени свободы для того, чтобы обеспечить правильное поведение его компонент при координатных преобразованиях. Дополнительные степени свободы подчиняются некоторым связям, которые необходимо учитывать при выводе уравнений поля.

    В современной теории поля разработан метод, который позволяет отделить динамическую часть от части не несущей физической информации [20]. Этот формализм в современной теории поля называется каноническим. У него есть два существенных свойства. Первое заключается в том, что уравнения поля имеют первый порядок относительно производных по времени. Второе свойство заключается в явнов выделении времени в лоренц - инвариантной теории (так называемое 3+1 расщепление). В классической механике этот формализм совпадает с формализмом Гамильтона.

    Для получения этого формализма в общей теории относительности необходимо записать плотность действия в линейном относительно первых производных виде (этот вид называется записью в форме Паллатини). Обычный интеграл действия:

    \begin{displaymath} S=-\kappa \int d^4 x \sqrt{-g} R \end{displaymath}

    дает уравнения общей теории относительности при варьировании метрического тензора $g_{\mu \nu}$. Получившиеся уравнения Эйлера являются дифференциальными уравнениями в частных производных второго порядка относительно метрического тензора. Однако, те же уравнения можно привести к каноническому гамильтонову виду:

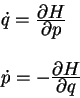
    \begin{displaymath} \begin{array}{l} \dot q ={\displaystyle\partial H\over\displ... ...isplaystyle\partial H\over\displaystyle\partial q} \end{array}\end{displaymath}

    Для этого представим плотность лагранжиана гравитационного поля в форме Палатини, при этом символы Кристоффеля рассматриваются как независимые переменные:
    \begin{displaymath} S=-\kappa \int d^4 x \sqrt{-g} g^{\mu \nu} R_{\mu \nu}(\Gamma) \end{displaymath} (9.5)

    где

    \begin{displaymath} R_{\mu \nu}(\Gamma) \equiv {\displaystyle\partial \Gamma^{\a... ...ta} - \Gamma^{\alpha}_{\mu \beta} \Gamma^{\beta}_{\alpha \nu} \end{displaymath}

    Здесь следует отметить, что ковариантные компоненты тензора Риччи не содержат метрического тензора, а содержат только бинарные произведения символов Кристоффеля и их производных по координатам. Варьируя (9.5) по метрическому тензору получаем уравнения Эйнштейна:
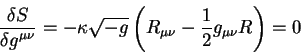    \begin{displaymath} {\displaystyle\delta S\over\displaystyle\delta g^{\mu \nu}} ... ...\displaystyle 1\over\displaystyle 2} g_{\mu \nu} R \right) = 0 \end{displaymath} (9.6)

    Дополнительно к этим уравнениям получаем уравнения связи, которые устанавливают соотношения между независимыми величинами $g_{\mu \nu}$ и $\Gamma^{\alpha}_{\mu \nu}$:

    \begin{displaymath} {\displaystyle\partial \sqrt{-g} g^{\mu \nu}\over\displaysty... ...ha} - \sqrt{-g} g^{\mu \nu} \Gamma^{\beta}_{\beta \alpha} = 0 \end{displaymath}

    решая эти уравнения относительно величин $\Gamma^{\alpha}_{\mu \nu}$ получаем обычную зависимость между символами Кристоффеля и метрическим тензором:

    \begin{displaymath} \Gamma^{\alpha}_{\mu \nu} = {\displaystyle 1\over\displaysty... ...eta, \alpha} + g_{\nu \beta, \mu} - g_{\mu \nu, \beta} \right) \end{displaymath}

    9.3 Источник гравитационного поля

    В предыдущем параграфе получены уравнения общей теории относительности в вакууме. Полные уравнения должны содержать также влияние материи на гравитационное поле. Они должны содержать источник гравитационного поля. Полное действие для системы гравитационное поле + материя представляет из себя сумму двух членов: действия для гравитационного поля $S_g$ и действие для материи $S_m$. Полные уравнения поля получаются как сумма вариаций действия для поля и действия для материи:

    \begin{displaymath} \delta S_g + \delta S_m =0 \end{displaymath}

    Вариации производятся по метрическому тензору, а сами уравнения получаются из приравниванием к нулю первых производных Эйлера - Лагранжа от действия по метрическому тензору:
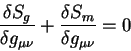    \begin{displaymath} {\displaystyle\delta S_g\over\displaystyle\delta g_{\mu \nu}... ...playstyle\delta S_m\over\displaystyle\delta g_{\mu \nu}} = 0 \end{displaymath} (9.7)

    Вариация от действия гравитационного поля по метрическому тензору есть (9.6):

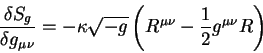
    \begin{displaymath} {\displaystyle\delta S_g\over\displaystyle\delta g_{\mu \nu}... ...- {\displaystyle 1\over\displaystyle 2} g^{\mu \nu} R \right) \end{displaymath}

    Вариации от $S_m$ по метрическому тензору называются тензором энергии - импульса:
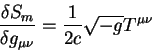    \begin{displaymath} {\displaystyle\delta S_m\over\displaystyle\delta g_{\mu \nu}... ...\displaystyle 1\over\displaystyle 2 c} \sqrt{-g} T^{\mu \nu} \end{displaymath} (9.8)

    Окончательно, уравнения гравитационного поля в общей теории относительности имеют вид:
    \begin{displaymath} R_{\mu \nu} - {\displaystyle 1\over\displaystyle 2} g_{\mu \nu} R ={\displaystyle 8 \pi G\over\displaystyle c^4} T_{\mu \nu} \end{displaymath} (9.9)

    Здесь постоянную ${\displaystyle 1\over\displaystyle 2 c \kappa}$ определяют из того условия, чтобы в пределе слабых полей и медленных движений уравнения общей теории относительности совпадали с уравнениями Ньютона для гравитационного поля.

    Приведем несколько примеров тензора энергии - импульса.

    Тензор энергии - импульса свободной частицы есть:
    \begin{displaymath} T_{\mu \nu} = \rho c^2 u_{\mu} u_{\nu} \end{displaymath} (9.10)

    Тензор энергии - импульса идеальной жидкости есть:
    \begin{displaymath} T_{\mu \nu} = (\rho c^2 + p) u_{\mu} u_{\nu} - g_{\mu \nu} p \end{displaymath} (9.11)

    Здесь $\rho$ - плотность частицы в первом примере и плотность жидкости во втором примере, $p$ - давление в жидкости во втором примере.

    Рекомендуемая и цитируемая литература

    1 Справочное руководство по небесной механике и астродинамике. под ред. Г.Н.Дубошина, М.: Наука, 1976.

    2 А.Лайтман, В.Пресс, Р.Прайс, С.Тюкольски. Сборник задач по теории относительности и гравитации. М.: Мир, 1979.

    3 Hafele J.C., Keating R.E., Around - the world atomic clocks: Predicted relativistic time gains, Science, v.177, p.166, 1972; Hafele J.C., Keating R.E., Around - the world atomic clocks: Observed relativistic time gains, Science, v.177, p.168, 1972.

    4 Briatore L., Leschiutta S., Evidence for the Earth gravitational shift by direct - time - scale comparison, Il Nuovo Cimento, v. B37, p.219, 1979.

    5 Iijima S., Fujiwara K., An experiment for the potential blueshift at the Norikura Corona Station. Annals of the Tokyo Astronomical Obsrvatory. Srcond Series. v.XVII, N 2, p.68, 1978.

    6 Vessot R.F.C., Levine M.W., A test of the equivalence principle using space born clock. General relativity and Gravitation. v.10, p.181, 1979.

    7 А.Эйнштейн. Физика и реальность. М.: Наука, 1965.

    8 Л.Д.Ландау, Е.М.Лифшиц. Теория поля. М.: Наука, 1988.

    9 Я.А.Схоутен. Тензорный анализ для физиков. М.: Наука, 1965.

    10 Wald R.M. General Relativity. The University of Chicago Press. 1984.

    11 С.М. Рытов, Ю.А. Кравцов, В.И. Татарский. Введение в статистическую радиофизику. часть II, Случайные поля. М.: Наука, 1978.

    12 С.Вейнберг. Гравитация и космология, М.: Мир, 1975.

    13 Эльсгольц Л.С. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1969.

    14 Гельфанд И.М. Лекции по вариационному исчислению. М. Физматгиз, 1956.

    15 А.Эйнштейн. Собрание научных трудов. т.I, стр. 65, статья 8, М.: Наука, 1965.

    16 А.Эйнштейн. Собрание научных трудов. т.I, стр. 189, статья 17, М.: Наука, 1965.

    17 А.Эйнштейн. Собрание научных трудов. т.I, стр. 227, статья 21, М.: Наука, 1965.

    18 А.Эйнштейн. Собрание научных трудов. т.I, стр. 448, статья 37, М.: Наука, 1965.

    20 Швингер Ю. Теория квантованных полей. М., 1956.

    В предметном указателе: Наука и техника | Научно-технический прогресс | Научно-технические достижения | Религиозные теории | О теориях мироздания | теория Большого взрыва | Теория вакуума | Теория возникновения вселенной | Ошибки теории относительности | Эфирные теории | Ошибки теории эфира | Единая теория поля | Теория суперструн | Черные дыры | Победа над смертью | Средства от старости | Свободнорадикальная теория | Мистические теории | Непознанное | тайное знание | Потустороннее существование | Бог | Стоячие ЭМ волны как пробный камень для альтернативных теорий | В.Дугин ТЕОРИЯ ПЕРВОВЕЩЕСТВА | Высшие технологии и теории | И. Изард Когнитивные теории эмоций | ИССЛЕДОВАНИЕ ИНФОРМАЦИОННОЙ ТЕОРИИ ЭМОЦИЙ | КРИЗИС РЕЛЯТИВИСТСКИХ ТЕОРИЙ | Основы теории эфира | Основы энерго-информационной теории | Свободнорадикальная теория старения | Таблица различий мистических теорий | Теории | Теория суперструн | Теория эмоций П. В. Симонова | Торсионные теории | Физические начала специальной теории относительности | Чем отличаются научные теории от религиозных | Шипов Теория физического вакуума | Флуктуация вакуума | СПЕЦИАЛЬНЫЕ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ новая редакция | Гравитация | Философия религии | Что такое религия | Эликсир бессмертия | Теории личности | Новое в теории появления жизни | Оптический диск высокой плотности | Революция в теории коммуникаций: открыт новый ти | Форум: О теориях | Форум: Теория чистого разума и абсолютного созна | Теория эфира Н.Теслы | Подтверждения релятивисткой теории | Современные теории эфира | Экспериментальная проверка теории относительност | Теория эфира | РАДИОАСТРОНОМИЯ ПОДТВЕРЖДАЕТ ТЕОРИЮ ЭЙНШТЕЙНА | Любарь В.Я. Теория пространств | Парадоксы теории относительности | Психологические теории эмоций | О теории относительности | А.А.Тяпкин. Об истории возникновения теории отно | Теория невероятности | Теория невероятности | О теории суперструн | Форум: Гайя-теория | Форум: Новая теория психотипов | Теория петлевой квантовой гравитации | Триангулярная теория любви Стернберга | Утверждение теории Большого взрыва | Теории мироздания | Теория суперструн Дэвид Гросс | Бесконечно ли всемогущество теории суперструн? И | В. Дугин Теория первовещества Аннотация | Птицы Дарвина подтвердили теорию эволюции | Пульсар подтвердил теорию Эйнштейна с точностью | Два способа расчета плотности тёмной материи А.В | Новый динозавр подтверждает теорию Дарвина | Теория противоречивости бытия | Спутник NASA подтвердил теорию Эйнштейна | Волосатое подтверждение теории Дарвина | ОТНОСИТЕЛЬНОЕ ВРЕМЯ И АБСОЛЮТНАЯ ИДЕЯ | Проведена новая проверка специальной теории отно | Американец опубликовал единую теорию всех взаимо | Форум печать всей темы: Гайя-теория | Форум печать всей темы: О теориях | Форум печать всей темы: Теория чистого разума и | Форум печать всей темы: Новая теория психотипов | Форум печать всей темы: ТЕОРИЯ СУЩНОСТНОГО КОДИР | Теория относительности и психология | Выживаемость молоди рыб зависит от плотности поп | Моя теория | Описание для Различия сведений и знаний, относящ | Форум печать всей темы: Развитие Общей теории от | Форум печать всей темы: Парадокс теории относити | Форум печать всей темы: Теория информации | Форум печать всей темы: Когнитивная теория эмоци | ТЕОРИЯ ПОНЯТИЙ | Относительность неравенств Белла или Новый ум го | Обмен технологиями и высокая плотность населения | Классификации теорий юмора | О необходимости теории понятий | Теория юмора Константин Глинка | Форум печать всей темы: Теория Упругой Вселенной | Дискуссия фуко хабермас: вопросы теории власти | Теория опасности | 21-летний эксперимент вновь подтвердил теорию Да | Форум печать всей темы: Высшая Тионевая Теория М | Физики снова подтвердили общую теорию относитель | Теория психической коммуникации | Шипов Теория физичес C66080A0 | Рекомендация: Теории Мироздания | СПЕЦИАЛЬНЫЕ ТЕОРИИ О A7B49D52 | Эфирная теория | Эфирная теория- | Рекомендация: Запрещает ли теория СТО долететь д | Мифы: Запрещает ли теория СТО долететь до дальни | Форум печать всей темы: Вопрос. Теория нелинейны | Форум печать всей темы: Блондинка про теорию отн | Форум печать всей темы: Моя статья \"Теория | Форум печать всей темы: Теория Всего от Athene | Форум печать всей темы: Теория Всего от Athene's | Форум печать всей темы: Теория познания? Это оче | Форум печать всей темы: Теория происхождения неф | Форум печать всей темы: ТЕОРИЯ РАЗВИТИЯ ОБЩЕСТВА | Форум печать всей темы: Теория расходования дене | Люди верят в теории заговора из естественной пот | СТО и более общая теория | Форум печать всей темы: теория и практика | Форум печать всей темы: Теории национализма и на | Эфирная теория Мироздания | Эфирная теория Мироздания ССВ. Окончательный вид | Наброски единой теории поля. | Возможные следы жизни в метеоритах | Нонэссединамика - Теория Мироздания | попытка построения теории шахмат | попытка построения теории шахмат часть5 | попытка построения теории шахмат. часть 2. | попытка построения теории шахмат. Часть 3. | попытка построения теории шахмат. Часть 4 | Форум печать всей темы: ПОПЫТКА ПОСТРОЕНИЯ ТЕОРИ | Форум печать всей темы: Что колеблется?(теория с
    Последняя из новостей: Польза сна
    В статье будет показано как сон поддерживает информационную функциональность, помогая приспосабливаться к окружающему и событиям. Соответственно, можно будет ясно понимать, к каким потерям приводят нарушения сна в фазе сновидений и вообще каков вред от лишения сна или его укорочения:
    Польза сна.
    Революции напрасны в молодых странах
    Более пожилое население, как правило, указывает на существование зрелых и сложных обществ. В странах с населением старше 35 лет революций просто нет.
    На этой странице:посетителейзаходов
    сегодня:11
    вчера:1016
    Всего:1062713330
    Из коллекции изречений:
    >>показать еще...
    • Авторские права сайта Fornit