Найдено вещество с гигантским значением диэлектрической проницаемости
|
Группе ученых из Германии, Индонезии, Нидерландов и России удалось обнаружить в веществе с химической формулой La15/8Sr1/8NiO4 гигантское значение диэлектрической проницаемости — около 105 (а при определенных условиях — и на порядок выше, 106). Эта керамика имеет хорошие перспективы для технологических решений в микроэлектронике, поскольку сохраняет это значение диэлектрической проницаемости даже в присутствии переменного электрического поля с частотой вплоть до 1 Ггц.
Основной тенденцией в развитии микроэлектроники является миниатюризация и увеличение быстродействия различных устройств. Для запоминающих устройств вроде динамической и статической оперативной памяти, основанных на емкостных компонентах (конденсаторах), это означает, что при уменьшении размеров конденсатора величина его емкости должна оставаться прежней.
Из школьного курса известно, что емкость конденсаторов определяется геометрией прибора и ε среды, которая его заполняет (ε — безразмерная величина, зависящая от конкретного вещества). Для примера рассмотрим простейший случай — плоский конденсатор. Его емкость прямо пропорциональна площади обкладок и обратно пропорциональна расстоянию между ними. Важно здесь то, что существует также линейная зависимость емкости от диэлектрической проницаемости вещества, которое заполняет пространство между обкладками. Следовательно, степень миниатюризации определяется диэлектрической проницаемостью: имея в распоряжении вещество с большим значением ε, можно добиться существенного увеличения емкости конденсатора при его неизменных размерах.
На роль такого вещества могли бы претендовать — со спонтанной поляризацией в отсутствие внешнего электрического поля, некий аналог (о том, что такое поляризация, будет еще сказано ниже). Диэлектрическая проницаемость сегнетоэлектриков может достигать десятков тысяч (у первого открытого сегнетоэлектрика — — ε достигает 104). Однако проблема в том, что диэлектрическая проницаемость сегнетоэлектриков очень сильно зависит от температуры: выше определенной температуры (называемой по аналогии с ферромагнетизмом «температурой Кюри») диэлектрическая проницаемость вещества резко уменьшается. Кстати, из-за наличия таких качественных аналогий со свойствами ферромагнетиков, как зависимость проницаемости от температуры, существование , наличие , сегнетоэлектрики часто называют также ферроэлектриками.
Казалось бы, решению температурной проблемы должно было помочь открытие в 2000 году вещества с высокой диэлектрической проницаемостью CaCu3Ti4O12 (сокращенно его обозначают аббревиатурой CCTO), не являющегося сегнетоэлектриком. Проницаемость этой керамики при комнатной температуре составляет порядка 105 (для монокристаллического образца; у поликристаллических образцов она на порядок меньше) и остается практически постоянной в широком диапазоне температур от 100 до 600 К. Но у этого вещества обнаружился другой недостаток: диэлектрическая проницаемость CCTO сильно уменьшается в присутствии высокочастотного переменного электрического поля — с 105 до 102 при частоте поля 1 Ггц. Это сильно ограничивает практическое использование CCTO, поскольку в компьютерных и телекоммуникационных технологиях частота переменного электрического поля превышает этот частотный предел.
|
Таким образом, для эффективного увеличения емкости конденсатора кроме проблемы температурной зависимости диэлектрической проницаемости надо решить еще и проблему ее частотной зависимости — то есть найти вещество, которое будет слабо менять свою проницаемость с частотой. И, похоже, такое вещество было обнаружено. Об этом сообщается в , не так давно появившемся в Архиве. Группа ученых из Германии, Индонезии, Нидерландов и России изучила диэлектрические свойства керамики с химической формулой La15/8Sr1/8NiO4 (аббревиатура LSNO), более многообещающего с точки зрения технологического применения в микроэлектронике. Название статьи говорит само за себя: («Гигантское значение диэлектрической проницаемости при частоте вплоть до 1 Ггц при комнатной температуре»).
В чём причина зависимости диэлектрической проницаемости от частоты электрического поля? Дело в том, что частицы диэлектрика (атомы, молекулы, ионы) под действием электрического поля (постоянного или переменного — пока что не важно) превращаются в диполи вследствие раздвижения положительных и отрицательных зарядов, из которых построены эти частицы. (Впрочем, в некоторых диэлектриках диполи существуют уже изначально, без внешнего воздействия.) Под действием поля происходит также ориентация диполей. При этом положительные полюса всех диполей оказываются сдвинутыми в направлении поля, а отрицательные — в противоположном направлении. В физике такой процесс характеризуют векторной величиной, связанной с каждого диполя и их плотностью (дипольный момент — это произведение модуля положительного или отрицательного заряда диполя на расстояние между этими зарядами, называемое плечом диполя). Эта величина, равная сумме всех дипольных моментов, образованных в диэлектрике под действием электрического поля в единице объема вещества, называется вектором поляризации, а сам процесс называется поляризацией. Вектор поляризации связан с вектором напряженности внешнего поля через диэлектрическую проницаемость линейным образом: чем больше значение ε, тем сильнее поляризовано вещество при заданной напряженности внешнего поля.
Теперь можно перейти к объяснению частотной зависимости диэлектрической проницаемости. Как уже было сказано выше, поскольку при наличии электрического поля диэлектрик «состоит» из диполей, то их ориентация или смещение в этом поле требуют определенного времени, называемого временем релаксации. Проще говоря, когда частота переменного электрического поля небольшая, то образующиеся диполи успевают ориентироваться в направлении этого поля, попеременно вместе с ним меняя направление дипольного момента, а значит, ε не изменяет своего значения. По мере увеличения частоты диполи перестают успевать ориентироваться по полю, более того — практически не происходит разделения зарядов. А раз поляризация диэлектрика с увеличением частоты электрического поля уменьшается, автоматически уменьшается и диэлектрическая проницаемость среды.
Здесь надо упомянуть еще и о таком важном понятии (которое пригодится для дальнейшего понимания), как диэлектрические потери, когда часть энергии переменного (непостоянного) электрического поля переходит в тепло. Если происходит изменение значения и направления напряженности электрического поля, то вектор поляризация также меняет величину и направление. Эти диполи испытывают соударения с другими диполями (частицами), что в конечном итоге приводит к рассеянию энергии. Если время релаксации значительно больше, чем период изменения внешнего поля, то есть если поле высокочастотное, то поляризация почти не успевает развиться, и диэлектрические потери очень малы. При малых частотах, когда время релаксации значительно меньше периода переменного электрического поля, поляризация следует за полем и диэлектрические потери также невелики, так как невелико число переориентаций диполей в единицу времени. Диэлектрические потери имеют максимальное значение, когда частота внешнего поля численно близка к обратному времени релаксации.
Численно величину диэлектрических потерь принято характеризовать в виде тангенса угла δ диэлектрических потерь: tgδ. Угол здесь возникает по следующей причине. В конденсаторе с идеальным диэлектриком, то есть диэлектриком без потерь, сила тока опережает напряжение по фазе на 90°. Если изобразить эту ситуацию в векторном виде, то вектора силы тока будут перпендикулярны векторам напряжения. Для реальных диэлектриков эти вектора не перпендикулярны, а образуют угол 90° – δ. В формуле для подсчета энергии, которая (рассеялась) в диэлектрике, фигурирует тангенс угла δ, отсюда и такая численная характеристика — тангенс, которую вводят для удобства расчета.
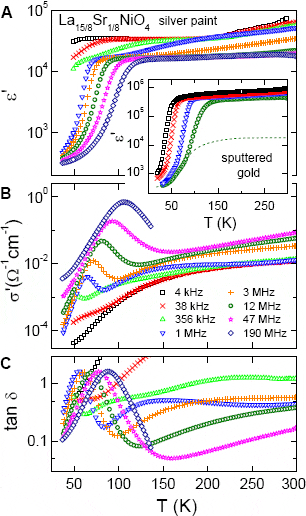
После теоретического экскурса в физику диэлектриков вернемся к обсуждаемой статье. В начале статьи авторы приводят экспериментальные кривые температурной зависимости диэлектрической проницаемости, проводимости и тангенса угла диэлектрических потерь монокристалла La15/8Sr1/8NiO4 (рис. 2) для различных частот внешнего переменного электрического поля, из которых видны следующие факты: 1) в области низких температур диэлектрическая проницаемость испытывает скачок с 300 до 17 000 и остается практически постоянной вплоть до комнатной температуры; 2) при комнатной температуре и в области низких частот ε составляет около 50 000; 3) изменив условия эксперимента, можно увеличить диэлектрическую проницаемость исследуемой керамики до 106 (см. график во вставке на рис. 2A); 4) проводимость (рис. 2B) и тангенс (рис. 2C) диэлектрических потерь в LSNO имеют ярко выраженные пики, как и в керамике CCTO.
Последний, четвертый факт указывает на то, что диэлектрические потери в исследуемом учеными веществе, вероятно, могут быть объяснены тем же образом, что и в CCTO, то есть эффектом Максвелла–Вагнера.
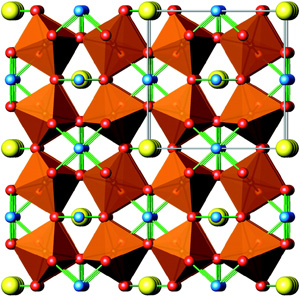
Этот эффект возникает в диэлектриках со сложной неоднородной кристаллической структурой, обладающих чередующимися слоями с высокой проводимостью электрического тока и слоями изоляции — физики такие вещества с неоднородными характеристиками, не только диэлектрическими, называют гетероструктурами. (На рис. 1 приведено несколько элементарных ячеек CaCu3Ti4O12; кристаллическая структура La15/8Sr1/8NiO4 исследователями в статье не приводится, но она не менее сложная, чем у CCTO. Оба вещества по своей кристаллической структуре относятся к типу .) Объясняется данный эффект тем, что заряды, образующиеся под действием внешнего электрического переменного поля на границах раздела проводящих и изоляционных слоев, можно рассматривать как диполи, направления моментов которых меняются вместе с изменением приложенного поля.
Далее всё как у «обычных» диэлектриков. При низких частотах межслойный заряд успевает полностью сформироваться, и диэлектрические потери оказываются малыми, так как поляризация находится «в фазе» с электрическим полем. При высоких частотах диэлектрические потери опять-таки малы, так как поверхностная поляризация не успевает устанавливаться вслед за электрическим полем. В области промежуточных частот диэлектрические потери велики, так как период колебаний напряженности электрического поля сопоставим со временем релаксации поверхностной поляризации. Диэлектрические потери из-за такой вот релаксации межслойной поляризации и называют эффектом Максвелла–Вагнера.
|
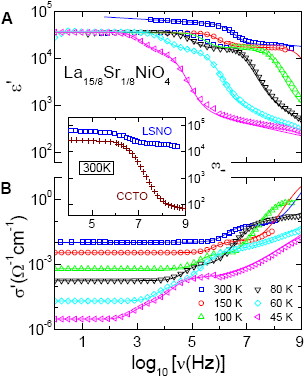
Основной результат, по мнению исследователей, состоит в измерении диэлектрической проницаемости и проводимости LSNO для высоких частот вплоть до гигагерцевой при разных температурах (рис. 3).
Чтобы была возможность, так сказать, почувствовать разницу, ученые привели частотную зависимость керамик LSNO и CCТО при комнатной температуре (см. вставку на рис. 3). Видно, что на частоте 1 Ггц ε образца La15/8Sr1/8NiO4 по-прежнему остается гигантской, превышая значение 104 — на фоне всего лишь относительно высокого (около 102) аналогичного значения у CCTO.
По мнению авторов, природа такого гигантского значения диэлектрической проницаемости у LSNO, скорее всего, может быть объяснена в рамках теории эффекта Максвелла–Вагнера. При этом некоторую роль должны играть и поверхностные эффекты; см. экспериментальные кривые графиков из рис. 2A, на которых легко увидеть различие на порядок диэлектрической проницаемости исследуемого вещества, контактирующего сначала с серебряными электродами (εmax ~ 105 при комнатной температуре), а затем с золотыми (в этом случае ε LSNO составляет уже 106).
В любом случае, несмотря на некоторые неясности в происхождении таких гигантских значений диэлектрической проницаемости, практическое преимущество керамики La15/8Sr1/8NiO4 по сравнению с интенсивно изучаемой CCTO очевидны.
Источник: S. Krohns, P. Lunkenheimer, Ch. Kant, A. V. Pronin, H. B. Brom, A. A. Nugroho, M. Diantoro, A. Loidl. // препринт arXiv:0811.1556 (24 November 2008).
Юрий Ерин
http://www.scorcher.ru/xml/news.rss
|