Другая материя: Топологический прогноз

Кольца Борромео (слева) - один из примеров соединения Брунна (Brunnian link), удаление любого элемента которого ведет к высвобождению всех других элементов. Кольца Брунна (справа) - другой пример такого соединения. Состояние Ефимова аналогично топологии колец Борромео. Но петли, образующие соединение Брунна, могут формировать и более сложные структуры... ... и еще более сложные структуры...

Еще в 1970 году молодой советский физик сделал необычное предположение. Виталий Ефимов, который в настоящее время работает в Университете штата Вашингтон (США), показал, что квантовые объекты, которые не могут образовывать меду собой пары, могут формировать тройки. 

В 2006 году группа австралийских ученых обнаружила первый пример этого так называемого «состояния Ефимова» в холодном газе, состоящем из атомов цезия. 

На первый взгляд это может показаться нелогичным. Ведь связи, удерживающие вместе тройку объектов, точно такие же, как и в паре. Но на самом деле это не так, между ними существует тонкое, но важное различие. 

Сегодня Нильс Баас (Nils Baas) из Норвежского университета естественных и технических наук сделал другое смелое предсказание. Он утверждает, что странные связи, удерживающие вместе тройки атомов цезия, могут сформировать и более сложные структуры. Мы на грани открытия новой формы вещества, подчиняющейся незнакомой нам области физики, говорит Баас. 

За столь необычными выводами стоит исследование в области топологии – науке о форме. К вопросам, изучаемым топологией, относятся, в частности, свойства структуры объекта, которые сохраняются при его растяжении, сжатии, изгибе – но не разрушении. 

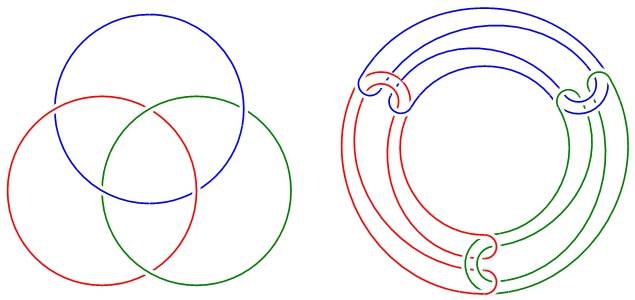
Показательный пример – фигура, известная как «кольца Борромео». Она состоит из трех кругов, переплетающихся таким образом, что при удалении любого из них два других окажутся расцепленными. 

Ключевой момент здесь состоит в том, что круги на плоскости не могут стать кольцами Борромео. Но стоит ввести третье измерение – и мы получим эту фигуру. При этом гипотетический «плоский наблюдатель», живущий в двумерном пространстве, будет немало озадачен этим свойством. 

Более того, между кольцами Борромео и структурой троек атомов цезия, предсказанной Ефимовым, существует формальная математическая аналогия. Математические формулы, описывающие квантовую механику состояния Ефимова и топологию колец Борромео, практически одинаковы. 

Хотя обычное вещество, по которому вы можете постучать костяшками пальцев, явно ограничено обыденным 3D, математика квантовой механики оперирует совершенно другим набором измерений. И в этом непостижимом пространстве и формируется аналогия колец Борромео. В результате можно говорить о некоей «параллельной» физике, законы которой оказывают неизбежное влияние на мир, в котором мы живем. И это воздействие проявляется не только на уровне связей между атомами. Физики создают проводники и изоляторы, движение электронов в которых определяется топологией квантовой механики. Так называемые топологические изоляторы сегодня открывают широкие горизонты перед учеными и инженерами. 

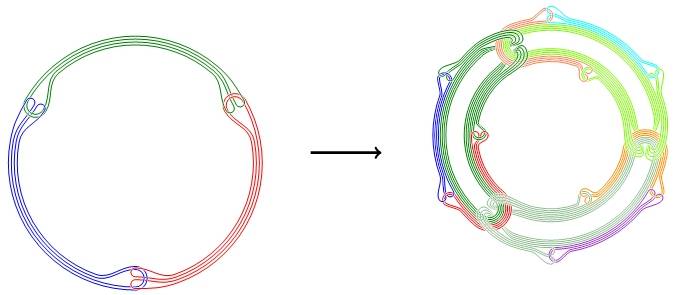
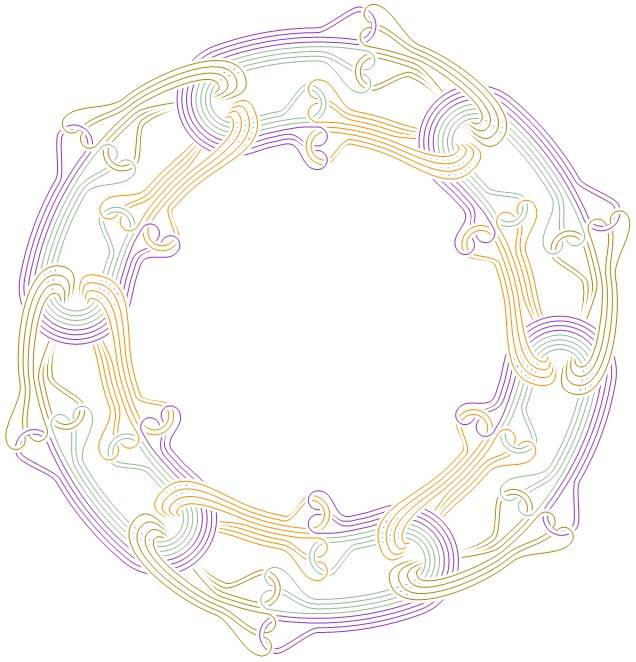
И если прогнозы Бааса верны, это только самое начало. По мнению ученого, кольца Борромео – лишь простейший пример из целого ряда топологических структур. Если возможно состояние Ефимова, эквивалентное кольцам Борромео, то можно реализовать и аналоги других, более сложных, структур. Такая материя будет пребывать в необычном состоянии, и её поведение будет описываться законами новой «физики Ефимова». 

Как будет вести себя такое вещество? Пока этот вопрос остается без ответа, но Баас предполагает несколько интересных возможностей. Взаимосвязь между частицами в состоянии Ефимова очень похожа на квантовую запутанность. Никто не может сказать наверняка, что это одно и то же, но если речь действительно идет о новом виде квантовой запутанности, то это будет иметь важные последствия для криптографии, квантовых вычислений и информатики в целом. 

Лауреат Нобелевской премии по физике Мюррей Гелл-Манн однажды заметил, что «Все, что не запрещено – является обязательным». Он имел ввиду способы взаимодействия частиц в квантовой механике: если нет никакой причины, по которой частицы не могут взаимодействовать определенным образом, то они должны так взаимодействовать. Возможно, теория Бааса раскрывает всю глубину этого утверждения. 

По сообщению The Physics arXiv Blog