Искусственные нейронные сети
Искусственные нейронные сети. Формальный нейрон. Основные нейросетевые парадигмы
В этой лекции я расскажу об исследованиях в области нейронных сетей. Эта область теоретических исследований чрезвычайно интересна, активно развивается, здесь есть множество различных подходов, концепций и моделей. Наиболее значимые теоретические направления и модели принято называть нейросетевыми парадигмами.
Конечно, я не могу рассказать обо всем этом многообразии исследований подробно, моя задача – дать наиболее общие представления об исследованиях нейронных сетей.
Сначала я кратко опишу модель формального нейрона, которая лежит в основе большинства нейронных сетей, затем расскажу об истории нейросетевых исследований, далее тоже кратко охарактеризую примеры нейросетевых парадигм, и в заключение сделаю комментарий о значении этих работ для эволюционной кибернетики.
1. Формальный нейрон
Большинство моделей основывается на схеме формального нейрона У.С.Мак-Каллока и У.Питтса (1943 год) [1], согласно которой нейрон представляет собой пороговый элемент (Рис.1). На входах нейрона имеются возбуждающие и тормозящие синапсы, в нейроне определяется взвешенная сумма (с учетом весов синапсов) входных сигналов, при превышении этой суммой порога нейрона вырабатывается выходной сигнал.
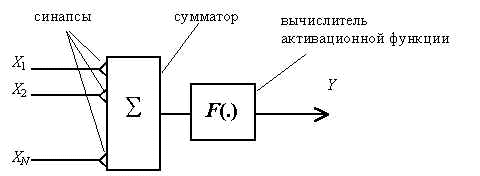
Рис. 1. Схема формального нейрона. Xi – входные сигналы, Y – выходной сигнал нейрона.
Работа формального нейрона (Рис.1) может быть описана уравнениями:
Yj = F(netj – Kj) , (1)
netj = i wji Xi , (2)
где j – номер нейрона в сети, Xi – входные сигналы, Yj – выходной сигнал нейрона, wji – веса синапсов, netj – суммарное входное воздействие на нейрон, Kj – порог нейрона, F(.) –активационная функция.
Активационная функция характеризует реакцию нейрона на входное воздействие netj , она может быть пороговой:

или некоторой непрерывной, например, линейной:
F(a) = ka (3a)
или логистической:
F(a) = 1/[1+exp(-a)] . (3b)
В зависимости от реализуемого алгоритма на допустимые значения входов и выходов нейрона накладываются определенные ограничения: значения Xi и Yj могут бинарными (т.е. равными 0 или 1), бинарными биполярными (+1 или -1), принадлежащими интервалу (0,1), неотрицательными или действительными. Аналогичные ограничения накладываются на веса синапсов нейронов wij .
Отметим, что в основополагающей работе Мак-Каллока и Питтса [1] входы и выходы нейронов предполагались бинарными, веса синапсов считались бинарными биполярными, а активационная функция – пороговой. Исследования нейросетей в [1] проводились с точки зрения анализа логических исчислений, которые могут быть построены на базе формальных нейронов. В частности было показано, что "для всякого логического выражения, удовлетворяющего некоторым условиям, можно найти сеть, имеющую описываемое этим выражением поведение" [1].
Формальные нейроны до определенной степени отражают динамику передачи сигналов в реальных биологических нейронах. Живые нейроны состоят тела клетки, дендритов и аксона. Очень упрощая картину, работу нейрона можно описать следующим образом. Дендриты получают сигналы от других клеток через синапсы, эти сигналы поступают в тело клетки, где они суммируются с другими такими же сигналами. Если суммарный сигнал в течение короткого промежутка времени является достаточно большим, то клетка возбуждается, вырабатывая в аксоне импульс, который передается на следующие клетки. Не вдаваясь в подробности, подчеркнем, что формальные нейроны только очень грубо отражают работу биологических живых нервных клеток.
2. Немного истории
2.1. Первый бионический бум. Перцептрон
История исследования нейронных сетей испытывала взлеты и падения. Первый всплеск энтузиазма был в 50-60-х годах. Его можно связать с работами Дж. фон Неймана по концептуальному сравнительному анализу работы биологических нейронных сетей и компьютеров [2] и по разработке принципов построения надежных вычислительных систем из ненадежных компонент (фактически формальных нейронов) [3] и с работами Ф.Розенблата по перцетронам [4]. Работы по перцептронам – наиболее значимое направление исследований первого бионического бума.
Кратко опишем работы по перцептронам, следуя в основном изложению, представленному в книге С.В. Фомина и М.В. Беркенблита "Математические проблемы в биологии" [5]. Перцепторон состоит из элементов 3-х типов: S - элементов, A - элементов и R - элемента (Рис.2) . S - элементы это – слой рецепторов. Эти рецепторы соединены с A - элементами, с помощью тормозных или возбуждающих связей. Каждый рецептор может находиться в одном из двух состояний – покоя или возбуждения. A - элементы представляют собой сумматоры с порогом (т.е. формальные нейроны). Это означает, что A - элемент возбуждается, если алгебраическая сумма возбуждений, приходящих к нему от рецепторов, превышает определенную величину – его порог. При этом сигнал от рецептора, приходящий по возбуждающей связи, считается положительным, а приходящий по тормозной связи – отрицательным. Сигналы от возбудившихся A - элементов передаются в сумматор R, причем сигнал от i-го ассоциативного элемента передается с коэффициентом ki.
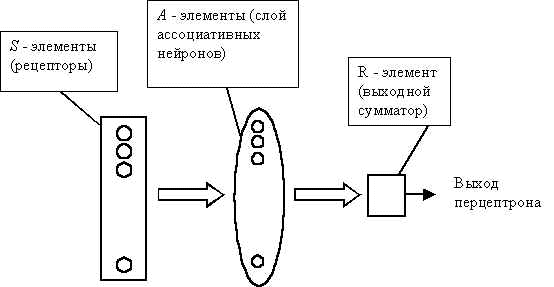
Рис. 2. Схема перцептрона.
Система связей между рецепторами S и A - элементами, так же как и пороги A - элементов выбираются некоторым случайным, но фиксированным образом, а обучение состоит лишь в изменении коэффициентов ki. Считаем, что мы хотим научить перцептрон разделять два класса объектов, и потребуем, чтобы при предъявлении объектов первого класса выход перцептрона был положителен, а при предъявлении объектов второго класса – отрицательным. Начальные коэффициенты ki полагаем равными нулю. Далее предъявляем обучающую выборку: объекты (например, круги либо квадраты) с указанием класса, к которым они принадлежат. Показываем перцетрону объект первого класса. При этом некоторые A - элементы возбудятся. Коэффициенты ki , соответствующие этим возбужденным элементам, увеличиваем на 1. Затем предъявляем объект второго класса и коэффициенты ki тех A - элементов, которые возбудятся при этом показе, уменьшаем на 1. Этот процесс продолжим для всей обучающей выборки. В результате обучения сформируются значения весов связей ki .
После обучения перцептрон готов работать в режиме распознавания. В этом режиме перцептрону предъявляются "не знакомые" перцептрону объекты, и перцептрон должен установить, к какому классу они принадлежат. Работа перцептрона состоит в следующем: при предъявлении объекта возбудившиеся A - элементы передают сигнал R - элементу, равный сумме соответствующих коэффициентов ki. Если эта сумма положительна, то принимается решение, что данный объект принадлежит к первому классу, а если она отрицательна – то второму.
Исследования перцептронов показали, что перцептроны способны обучаться, хотя способности их обучения довольно ограничены. Справедлива теорема о сходимости перцептрона, согласно которой независимо от начальных значений коэффициентов и порядка показа образцов при обучении перцептрон за конечное число шагов научится различать два класса объектов, если только существуют такие значения. Подчеркнем, что теорема ничего не говорит о том, какие классы могут быть разделены.
Исследования также показали, что слабые стороны перцептрона (в частности большое время обучения) в значительной степени связаны со случайностью связей между его элементами. Однако эта конструктивная особенность обеспечивает перцептрону и положительное качество – надежность: выход из строя заметного числа элементов перцептрона слабо сказывается на качестве его работы (Рис.3).
Первые успехи исследованиям перцептронов других нейросетей вызвал взрыв активности и энтузиазма. М. Минский, Ф.Розенблат, Б. Уидроу и другие разработали ряд искусственных нейронных сетей. В течение некоторого времени казалось, что ключ к интеллекту найден, и воспроизведение человеческого мозга является лишь вопросом конструирования достаточно большой сети.
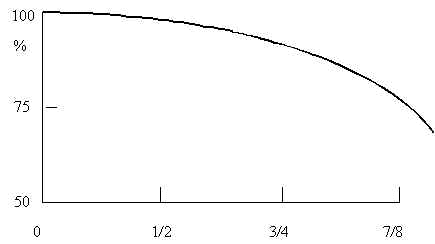
Рис.3. Поведение перцептрона при выходе из строя ассоциативных элементов. По оси ординат – процент правильных ответов, по оси абсцисс – доля выключенных ассоциативных элементов. Схематично.
Но эта иллюзия вскоре рассеялась. Возможности перцептронов оказались довольно ограниченными. Серьезный математический анализ перцептронов был проведен М.Минским и С. Пейпертом [6]. Они, в частности, показали, что задачи, которые в принципе могут быть решены перцептроном могут потребовать нереально больших времен или нереально большой памяти. Например, для различения некоторых классов объектов коэффициенты части ассоциативных элементов должны быть столь велики, что для хранения их в вычислительной машине потребовался бы больший объем памяти, чем для того, чтобы просто запомнить все конкретные объекты этих двух классов.
Критика перцептронов М. Минским (а он – один из признанных авторитетов в теории искусственного интеллекта), а также сравнительно небольшой прогресс нейрокибернетики 50-60 –х годов привели к тому, что период энтузиазма сменился периодом спада активности исследований искусственных нейронных сетей. Многие исследователи ушли в те области, которые им показались более привлекательными.
Только немногие кибернетики (Т. Кохонен, С. Гроссберг, Дж.Андерсон, Г.С. Бриндли, Д. Мар, В.Л.Дунин-Барковский, А.А.Фролов и др.) продолжали исследования нейросетей в 70-х годах.
2.2. Второй бионический бум
Однако в середине 80-х годов снова возник нейросетевой бум. Причиной бума, по-видимому, послужил постоянный интерес человечества к изучению работы нервной системы и ряд новых интересных моделей, разработанных к этому времени. Одной из таких "стимулирующих" моделей стали работы Дж.Дж. Хопфилда [7,8], которые позволили привлечь методы теоретической физики к исследованию нейронных сетей.
Во второй половине 80-х годов был предложен целый ряд интересных и содержательных моделей нейронных сетей. В моделях строятся нейросети, выполняющие различные алгоритмы обработки информации: ассоциативная память [7-11], категоризация, т.е. разбиение множества образов на кластеры, состоящие из подобных друг другу [12], топологически корректное картирование [13], распознавание зрительных образов, инвариантное относительно деформаций и сдвигов в пространстве [14], решение задач комбинаторной оптимизации [15]. Хотя ряд исследований посвящен анализу характеристик НС с целью понимания свойств естественных нейронных систем, подавляющее изобилие работ относится к исследованию алгоритмов нейросетей с прагматическими целями.
В большинстве моделей запоминание информации в нейронной сети (обучение) происходит в результате формирования весов синапсов нейронов. Во многих случаях это интерпретируется как формализация гипотезы Хебба [16], в соответствии с которой изменение состояния произвольного синапса определяется его текущим состоянием и активностью пре- и постсинаптических нейронов.
Предполагается, что определенные практические задачи должны решаться нейрокомпьютерами и нейрочипами – искусственными нейроподобными сетями, созданными на основе микроэлектронных вычислительных систем. Спектр задач для нейрокомпьютеров достаточно широк: распознавание зрительных и звуковых образов, создание экспертных систем и их аналогов, управление роботами, создание нейропротезов для людей, потерявших слух или зрение. Достоинства нейрокомпьютеров – параллельная обработка информации и обучаемость.
В 90-х годах активность по предложению новых нейропарадигм несколько снизилась, но зато нейросети и нейрочипы вошли в инженерный обиход, Например, одно из последних достижений – разработка нейрогентов, т.е. нейронных агентов (специализированных программ), предназначенных для оптимизации потоков пакетов информации в компьютерных сетях. Активно продолжается исследование характеристик различных нейросетей. Нейросетевые методы активно используются в новых кибернетических направлениях, таких как "Искусственная жизнь" и "Адаптивное поведение" – эти направления мы обсудим в следующих лекциях.
3. Ассоциативная память
Одно из ведущих направлений исследования нейронных сетей – ассоциативная память. Теория нейроподобной ассоциативной памяти была развита в фундаментальных работах Г.С. Бриндли, Д. Мара, Т. Кохонена, Г.Пальма, Д. Д.Уилшоу, В.Л.Дунина-Барковского, Дж.Хопфида, С.Амари, А.А.Фролова И.П. Муравьева и ряда лругих авторов.
Различают автоассоциативную и гетероассоциативную память. В обоих случаях имеется режим записи и режим воспроизведения.
В случае автоассоциативной памяти при записи происходит запоминание набора эталонных образов, задаваемых векторами Xk , k = 1,2,…, n ; а при воспроизведении по искаженному образу Xj + X (Xj – один из эталонов, X – вектор, характеризующий искажение) восстанавливается эталон Xj .
В случае гетероассоциативной памяти нейронная сеть при записи запоминает отображение Xk --> Yk между векторами Xk и Yk , k = 1,2,…, n ; при воспроизведении предъявляется один из эталонных векторов Xj (возможно несколько искаженный), и с помощью нейронной сети восстанавливается парный ему вектор Yj .
Ниже мы рассмотрим модель автоассоциативной памяти по Дж.Хопфилду и кратко охарактеризуем одну из наиболее популярных современных нейропарадигм – метод обратного распространения ошибок. Отметим, что нейронная сеть, реализующая метод обратного распространения ошибок может рассматриваться как гетероассоциативная память.
4. Сеть Хопфилда: нейронная сеть + гамильтониан
4.1. Общий подход
Отличительная черта работ Хопфилда - попытка применить физический подход к нейронным сетям. Ход рассуждений основополагающей работы Хопфилда примерно таков [7] . Допустим, что имеется некоторая физическая система, имеющая множество устойчивых особых точек: X1 , X2 , ... Эти точки могут рассматриваться как память устройства, реализуемого физической системой. Начиная с некоторой точки Xj + X (Xj – один из эталонов,X – вектор, характеризующий искажение), при малом X мы придем к Xj . Это вариант автоассоциативной памяти, в которой запомненный образ восстанавливается по искаженному образу.
Удобно построить физическую
систему, имеющую локальные минимумы энергии, соответствующие устойчивым особым
точкам. Для того чтобы систему можно было бы рассматривать как память, нужно
иметь большое число локальных минимумов. Пример физической системы с большим
числом локальных минимумов энергии – спиновые стекла, т.е. система спинов,
матрица обменных взаимодействий между которыми стохастична. (Модель спиновых
стекол кратко описана в
4.2. Схема нейросети
Схема нейросети по Хопфилду показана на Рис.4. Сеть состоит из N нейронов, все нейроны связаны со всеми, каждая связь характеризуется своим весом wij , матрица весов предполагается симметричной: wji = wij . Считаем, что N >> 1.
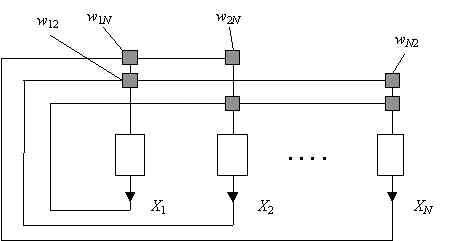
Рис.4. Схема нейронной сети
по Хофилду. ![]() – нейроны,
– нейроны, ![]() – синапсы
– синапсы
Состояние нейронной сети характеризуется вектором X = X1 , X2 , …, XN .
Каждый нейрон может находиться в двух состояниях Xi = 0 – покой, Xi = 1 – возбужденное состояние, i – номер нейрона.
4.3. Режим записи и режим воспроизведения
В режиме записи формируется матрица связей между нейронами wij , равная
wij = k (2Xki –1) (2Xkj –1), k = 1, 2, …, (4)
при i ![]() j
, wii = 0, – запоминаемые бинарные векторы, n – число
запоминаемых паттернов. Эталоны предполагаются случайными, компоненты векторов Xki
компоненты выбираются равными 0 либо 1 с равной вероятностью: p{Xki =
0} = p{Xki = 0}= 0,5.
j
, wii = 0, – запоминаемые бинарные векторы, n – число
запоминаемых паттернов. Эталоны предполагаются случайными, компоненты векторов Xki
компоненты выбираются равными 0 либо 1 с равной вероятностью: p{Xki =
0} = p{Xki = 0}= 0,5.
В процессе воспроизведения нейронная сеть функционирует в дискретном времени. Работа нейронной сети происходит в так называемом ассинхоронном режиме, т. е. в один такт времени только один нейрон может изменить свое состояние. Нейрон, которому разрешено менять состояние, выбирается стохастически. При этом нейроны работают как нейроны Мак-Каллока и Питтса с пороговой активационной функцией. А именно, полагаем:
Xj (t+1) = 1 при netj > 0 и Xj (t+1) = 0 при netj < 0 , (5)
netj = i wji Xi (t) , (6)
где t – момент "пересмотра" состояния j - го нейрона.
Работу нейронной сети в режиме воспроизведения можно рассматривать как динамическую систему. Покажем, что если число эталонов не слишком высоко, то эталоны соответствуют устойчивым состояниям (особым точкам) рассматриваемой динамической системы.
Оценим величину
nets j = i wji Xs i (t) , (7)
где Xs i (t) – компоненты какого-либо эталонного вектора. С учетом (4) имеем:
nets j = k (2Xkj –1) [i (2Xki –1) Xs i (t)] . (8)
В силу случайности эталонов
среднее значение величины в квадратных скобках равно 0 при s ![]() k и равно N/2 при s = k .
Следовательно, в силу такой псевдоортогональности имеем:
k и равно N/2 при s = k .
Следовательно, в силу такой псевдоортогональности имеем:
nets j ![]() (2Xs i
–1) N/2 .
(9)
(2Xs i
–1) N/2 .
(9)
Итак, имеем: nets j > 0 при Xs i = 1 и nets j < 0 при Xs i = 0.
Следовательно, за
исключением шума, возникающего от слагаемых с s ![]() k,
запомненные эталоны устойчивы.
k,
запомненные эталоны устойчивы.
4.4. Минимизация энергии нейронной сети
Определим "энергию" нейронной сети как
E = - 0,5 i ,j wji Xi Xj
, i
![]() j
(10)
j
(10)
Так как wji = wij , то изменение энергии, обусловленное текущим изменением состояния нейрона, равно
E = - Xj i wji Xi
= - Xj netj , i ![]() j.
(11)
j.
(11)
В силу (5) E ![]() 0 . Таким образом, алгоритм изменения состояний
нейронов приводит к монотонному уменьшению энергии. Состояния изменяются до тех
пор, пока не будет достигнут локальный минимум энергии. Энергия играет роль
функции Ляпунова для рассматриваемой динамической системы.
0 . Таким образом, алгоритм изменения состояний
нейронов приводит к монотонному уменьшению энергии. Состояния изменяются до тех
пор, пока не будет достигнут локальный минимум энергии. Энергия играет роль
функции Ляпунова для рассматриваемой динамической системы.
Формула энергии (10) совпадает с таковой для спинового стекла (см. лекцию 3). Для спиновых стекол известно, что число локальных минимумов энергии экспоненциально растет с ростом размерности системы N. Аналогия со спиновыми стеклами показывает, что в сети Хопфилда можно ожидать большое число локальных устойчивых состояний. Как показано выше, часть из этих состояний (в пренебрежении шумами) совпадает с записанными эталонами. Численный расчет, выполненный в [7], показал, что эталоны устойчивы, если отношение числа эталонов к числу нейронов не превышает величины 0,15. В дальнейшем эта оценка была уточнена аналитически с помощью методов статистической физики: было показано, что для устойчивости эталонов необходимо выполнение неравенства
n/N < 0,14 . (12)
Работа Хопфилда послужила мощным стимулом для исследований нейронных сетей физиками. Аналогия между нейронными сетями и спиновыми стеклами привлекла к нейронным сетям интерес большого числа физиков-теоретиков, которые стали записывать гамильтониан системы нейронов и исследовать свойства искусственных нейронных сетей высокоэффективными методами математической физики [17-19].
5. Метод обратного распространения ошибок
Здесь мы приведем только общее описание одного из важных и наиболее исследованных способов обучения нейронных сетей – метода обратного распространения ошибок [11]. Предполагается, что нейронная сеть имеет многослойную структуру (Рис.5). Нейроны сети представляют собой формальные нейроны с логистической активационной функцией (см. формулу (3b)). Сеть не имеет обратных связей: при вычислении выхода нейронной сети по ее входу сигналы нейронов передаются от слоя к слою, слева направо. Схема такой сети напоминает перцептрон (Рис.2). Иногда ее так и называют "обобщенный перцептрон".
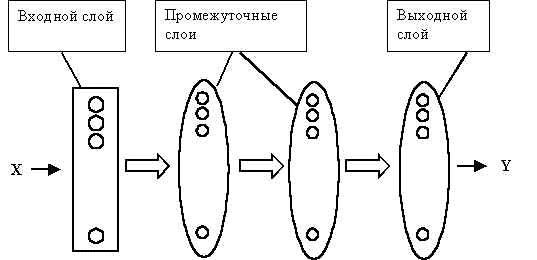
Рис.5. Схема нейронной сети, используемой в методе обратного распространения ошибок. Стрелками показано направление движения сигналов в процессе расчета выхода нейронной сети. При коррекции весов синапсов сигналы перемещаются в обратном направлении.
Нейронная сеть фактически реализует функцию гетероассоциативной памяти. Имеется режим обучения и режим воспроизведения.
В режиме обучения нейронная сеть запоминает отображение Xk --> Yk между векторами Xk и Yk , k = 1,2,…, n ; при воспроизведении предъявляется один из эталонных векторов Xj (возможно несколько искаженный), и с помощью нейронной сети восстанавливается парный ему вектор Yj .
Режим воспроизведения фактически тривиален: на вход нейронной сети поступают входные векторы X и в процессе функционирования формальных нейронов вычисляется выходной вектор Y .
Обучение многослойной нейронной сети осуществляется путем оптимизации весов синапсов методом градиентного спуска. Это обучение может быть представлено как последовательность следующих операций [20]:
- Выбрать очередную пару векторов Xk и Yk из обучающей выборки.
- Вычислить выход сети Y .
- Вычислить разность между выходом сети Y и требуемым выходным вектором Yk (целевым вектором обучающей пары). Т.е. определить ошибку нейронной сети.
- Подкорректировать веса сети wji так, чтобы минимизировать ошибку.
- Повторять шаги с 1 по 4 для каждой пары обучающей выборки до тех пор, пока ошибка не достигнет приемлемого уровня.
Все вычисления производятся послойно: в процессе расчета выхода нейронной сети по входу расчет идет слева направо, при корректировке весов рассчитываются всех нейронов и по этим ошибкам корректируются веса нейронов, при этом ошибки как бы "распространяются" в обратном направлении – справа налево. Процедура коррекции весов описана в многочисленной литературе. Здесь мы не будем воспроизводить ее, отметим только, что фактически коррекция весов означает минимизацию ошибки нейронной сети, а поиск минимума ошибки производится методом градиентного спуска.
6. Обсуждение
Таким образом, в настоящее время активно продолжаются исследования нейронных сетей и ведутся интенсивные работы по практическим применениям нейросетевых алгоритмов. Отметим, что, несмотря на все экономические трудности, работы по нейронным сетям в нашей стране активно продолжаются. В Москве уже более 20 лет под руководством В.Л.Дунина-Барковского ежемесячно проводится семинар по нейронным сетям. На базе этого семинара сформирована Российская ассоциация нейроинформатики, объединяющая энтузиастов-нейросетевиков. Ассоциация имеет широкие международные связи, под эгидой ассоциации проведен ряд конференций, симпозиумов, выставок, совещаний.
Необходимо подчеркнуть, что современные исследования нейронных сетей характеризуются внедрением в нейроинформатику высокоэффективных математических методов, заимствованных из статистической физики [17-19], синергетики [21], математической кибернетики [22], теории вероятностей [23], дифференциальной геометрии [24].
Однако, несмотря на чрезвычайную активность исследований по нейронным сетям и нейрокомпьютерам, многое в этих исследованиях настораживает. Изучаемые алгоритмы выглядят как бы "вырванным куском" из общего осмысления работы нервной системы. Исследуются те алгоритмы, для которых удается построить хорошие модели, а не наиболее важные для понимания свойств мышления, работы мозга и для создания систем искусственного интеллекта.
Настораживает также чрезмерная упрощенность понимания работы нейронный сетей, при котором нейроны рассматриваются как суммирующие пороговые элементы, а обучение сети происходит путем модификации синапсов. Ряд исследователей рассматривают нейрон как значительно более сложную систему обработки информации, предполагая, что основную роль в обучении играют молекулярные механизмы внутри нейрона [25-27]. В частности, в цикле работ Л.Е. Цитоловского с сотрудниками экспериментально продемонстрировано изменение порога командных нейронов (а не весов синапсов) при выработке и угашении условного рефлекса, и построены математические модели, демонстрирующие возможный механизм внутринейронного молекулярного обучения [28-30].
Все это указывает на необходимость максимально полного понимания работы биологических систем обработки информации и свойств организмов, обеспечиваемых этими системами. По моему мнению, одним из важных направлений исследований, способствующих такому пониманию, может быть анализ того, как в процессе биологической эволюции возникали "интеллектуальные" свойства биологических организмов. По-видимому, наиболее интересные исследования, направленные на изучение интеллектуальных свойств биологических организмов, ведутся сейчас в направлениях исследований "Искусственная жизнь" и "Адаптивное поведение", которые мы рассмотрим в следующих лекциях.
Литература:
- Мак-Каллок У.С., Питтс У. Логическое исчисление идей, относящихся к нервной активности // Автоматы, под ред. Шеннона К.Э. и Маккарти Дж. М.: ИЛ, 1956. С. 362 - 384.
- Фон Нейман Дж. Теория самовоспроизводящихся автоматов. М.: Мир, 1971, 382 с.
- Фон Нейман Дж. Вероятностная логика и синтез надежных организмов из ненадежных компонент. // Автоматы, под ред. Шеннона К.Э. и Маккарти Дж. М.: ИЛ, 1956. С. 68 - 139.
- Розенблат Ф. Принципы нейродинамики. Перцептроны и теория механизмов мозга. Мир, 1965.
- Фомин С.В., Беркенблит М.Б. Математические проблемы в биологии. М.: Наука, 1973, 200 с.
- Минский М., Пейперт С. Перцептроны. Мир, 1971.
- Hopfield J.J. Neural networks and physical systems with emergent collective computational abilities // Proc. Natl. Acad. Sci. USA. 1982. V.79. N.8. P.2554-2558.
- Hopfield J.J. Neurons with gradual response have collective computational properties like those of two-state neurons // Proc. Natl. Acad. Sci. USA. 1984. V.81. N.10. P.3088-3092.
- Фролов А.А., Муравьев И.П. Нейронные модели ассоциативной памяти. М.: Наука, 1987. 160 с.
- Фролов А.А., Муравьев И.П. Информационные характеристики нейронных сетей. М.: Наука, 1988. 160 с.
- Rumelhart D.E., Hinton G.E., Williams R.G. Learning representation by back-propagating error // Nature. 1986. V.323. N.6088. P. 533-536.
- Carpenter G.A., Grossberg S. A massively parallel architecture for selforganizing neural pattern recognition machine // Comput. Vision, Graphics, Image Process. 1987. V.37. N.1. P. 54-115.
- Kohonen T. Self-organized formation of topologically correct feature maps // Biol.Cybern. 1982. V.43. N.1. P.56-69.
- Fukushima K. Neocognitron: A hierarchical neural network capable for visual pattern recognition // Neural networks. 1988. V.1. N.2. P.119-130.
- Hopfield J.J., Tank D.W. Computing with neural circuits: A model. // Science. 1986. V.233. N.464. P.625-633.
- Hebb D.O. The organization of behavior. A neuropsychlogical theory. N.Y.: Wiley & Sons, 1949. 355 p.
- Amit D.J., Gutfreund H., Sompolinsky H. Spin-glass model of neural networks // Physical Review A. 1985. V.32. N.2. P.1007-1018.
- Amit D.J., Gutfreund H., Sompolinsky H. Storing infinite number of patterns in a spin-glass model of neural networks // Physical Review Letters. 1985. V.55. N.14. P.1530-1533.
- Gutfreund H. Neural networks with hierarchically correlated patterns // Physical Review A. 1988. V.37. N.2. P.570-577.
- Уоссермен Ф. Нейрокомпьютерная техника. Теория и практика. М.: Мир, 1972. 238 с.
- Хакен Г. Информация и самоорганизация: Макроскопический подход к сложным системам. М.: Мир, 1991. 240 с.
- Poggio T., Girosi F. Networks for approximation and learning // Proceedings of the IEEE. 1990. V.78. N.9. P.1481-1497.
- Amari S. Mathematical foundations of neurocomputing // Proceedings of the IEEE. 1990. V.78. N.9. P.1443-1462.
- Amari S. Dualistic geometry of manifold of higher-order neurons // Neural networks. 1991. V.4. P.443-451.
- Либерман .Е.А. Молекулярная вычислительная машина клетки (МВМ). Общие соображения и гипотезы // Биофизика. 1972. Т.17. N.5. С.932-943.
- Conrad M. Evolutinary learning circuits // J. Theor. Biol. 1974. V.46. N.1. P.167-188.
- Цитоловский Л.Е. Интегративная деятельность нервных клеток при записи следа памяти // Успехи физиол. наук. 1986. Т.17. N.2. С.83-103.
- Бабкина Н.В., Цитоловский Л.Е. Активный электрогенез командных нейронов оборонительного поведения моллюсков при обуславливании // Журн. высш. нерв. деят. 1991. Т.41. N.2. С.781-787.
- Саакян Ю.З., Цитоловский Л.Е. Модель химической памяти нейрона // Биофизика. 1990. Т.35. N.3. С.518-519.
- Саакян Ю.З., Россохин А.В., Цитоловский Л.Е. Математическая модель плаcтичности нейрона // Биофизика. 1993. Т.38. N.3. С.471-477.
Copyright © Vladimir Red'ko, Nov 2, 1999 ( redko@keldysh.ru )