Как и всякая другая волна, электронная волна Y(x,t) может быть стоячей волной. Для этого нам необходимо сложить две волны с одинаковыми амплитудами, движущиеся навстречу друг другу:




.


Волна как волна, с узлами и пучностями, но вместо, скажем, закрепленных концов струны в точках с координатами x=-l/2 и x=+l/2 нам при значениях координат x£-l/2 и x³+l/2 нужно иметь U=¥ - правее и левее выделенного интервала возможно решением будет . Используя условие непрерывности Y-функции, можно определить значение (комплексной) амплитуды y₀.

Для простоты внутри интервала будем считать U=0. Ведь потенциальная энергия определена с точностью до произвольной константы.

Для существования стоячей волны необходимо выполнение условия и, следовательно, при U=0 будет:


; .


Мы получили весьма важный результат: электрон в состоянии стоячей волны может иметь лишь вполне определенные дискретные значения энергии E_n. Энергия электрона квантуется! И при этом минимальное значение его энергии определяется линейными размерами потенциальной ямы, что существенно для дальнейшего.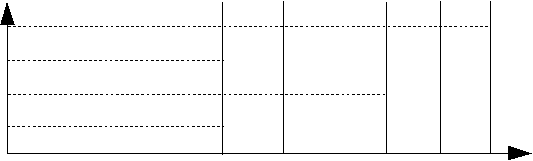





0 x

U=¥ U=0 U=¥ U=0 U=¥ U=0
 






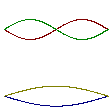
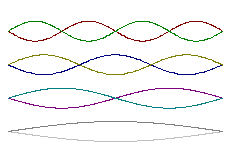
Любопытно провести такое исследование полученного результата. Подсчитаем силу, с которой электрон действует на стенку потенциальной ямы.

Очевидно,


.


А теперь попробуем получить выражение для силы F_x на основе корпускулярных представлений. При отражении электрона от стенки последней будет передан импульс 2p. При этом частота ударов определяется временем движения электрона между ударами


.


Выражение для силы мы получим, если разделим переданный импульс на это время:

.


Мы получили для силы то же значение, но это не означает, что в этой задаче волновой и корпускулярных подходы равноправны. При корпускулярном рассмотрении энергия электрона E произвольна, при волновом - она квантуется.

Поэтому, хотя волновое представление для нас, может, в чем-то не до конца понятно, корпускулярное представление следует назвать просто непонятным. При его использовании мы не сможем объяснить квантование энергии электрона.


К задаче о стоячих волнах Y-функций мы еще вернемся, а сейчас просто необходимо поговорить о смысле этой функции.


18.5. Физический смысл волновой функции


Высказанная де Бройлем гипотеза была проверена экспериментально, Шредингер написал волновое уравнение для некоторой Y-функции, полученные с помощью уравнения результаты для длины волны также подтверждаются экспериментом. И осталось всего лишь понять, что это за функция, колебания чего распространяются при движении электрона.

Здесь мы с Вами вступаем на весьма зыбкую почву. Говоря о смысле Y-функции, легко попасть в какую-нибудь ловушку, высказать утверждение, которое вступает в противоречие (или кажущееся противоречие) с некоторыми из многочисленных экспериментально наблюдаемых эффектов. “Ибо сказано: мысль изреченная есть ложь”. И хотим мы этого или не хотим, мы будем пытаться объясниться на “старом” языке, используя знакомые и привычные понятия и термины. Другого языка мы просто не знаем:


“Раз поведение атомов так не похоже на наш обыденный опыт, то к нему очень трудно привыкнуть. И новичку в науке, и опытному физику - всем оно кажется своеобразным и туманным. Даже большие ученые не понимают его настолько, как им хотелось бы, ...” ¹


Вдумайтесь в эти слова. Сказано, собственно, что даже большие ученые пытаются объяснить поведение квантового микрообъекта с помощью представлений, справедливых для макрообъекта. Это безнадежное занятие, мы подошли к той границе, за которой действуют уже другие законы и требуется иной способ мышления. Но - хочется продолжать рассуждать по-старому. Такие рассуждения не приводят к правильным результатам и отсюда происходит ощущение непонятности.

Эта непонятность поведения атомов и других мельчайших частиц вела “ко все большему замешательству среди физиков”. И вот,


“В 1926-1927 гг. оно было устранено работами Шрёдингера, Гейзенберга и Борна. Им удалось в конце концов получить непротиворечивое описание поведения вещества атомных размеров.” ²


Это “непротиворечивое описание” в общих чертах таково. Квантовое поведение микрочастицы описывается волновым уравнением Шрёдингера, для нее справедлив принцип неопределенностей, но при этом волновой функции приписывается чисто математический смысл:


“... волновая функция, удовлетворяющая уравнению, не похожа на реальную волну в пространстве; с этой волной нельзя связать никакой реальности, как это делается со звуковой волной.” ³


Y-волну для электрона часто называют просто электронной волной. Но употребления этого термина в то же время всячески пытаются избежать. Вместо этого говорят про волну амплитуды плотности вероятности. Смысл термина вот в чем. Энергия колебаний пропорциональна квадрату амплитуды колебаний. Поток энергии при распространении волны пропорционален квадрату ее амплитуды. Подобно этому пропорциональной квадрату амплитуды плотности вероятности оказывается некоторая плотность вероятности.

Собственно, одну трудность заменили другой. На основе классических представлений нельзя понять, как ведет себя электрон в атоме. Но разве можно понять, как не связанная ни с какой реальностью волна амплитуды плотности вероятности дифрагирует на реальной кристаллической решетке? Однако, такая “непонятность” мало беспокоила теоретиков.

Констатировав, что на “старом” языке классической физики объяснить вновь открытые явления не удается, нам предлагается не новый язык, а просто говорят: “Поведение электрона описывается Y-функцией, которая физического смысла не имеет, она имеет лишь математический смысл.”

Не удивительно, что “новичку” при знакомстве с квантовой физикой “все кажется своеобразным и туманным”. И при этом саму непонятность предлагаемых объяснений предлагается считать особенностью, свойством квантовой физики.


Рискуя вызвать гнев коллег - физиков, я хочу все-таки попытаться хоть что-то сделать понятным. Впрочем, я буду рассуждать, а соглашаться со мной или нет - Ваше дело. Думайте.


19.1. Как нам это объясняют


Всякого рода объяснения я склонен делить на такие, которые понять трудно, и такие, которые понять нельзя. Вот какие объяснения я лично не понимаю и, мне кажется, понять их нельзя. Для начала цитата из учебника (!) И.В.Савельева:


“Иногда соотношение неопределенностей получает следующее толкование: в действительности у микрочастицы имеются точные значения координат и импульсов, однако ощутимое для такой частицы воздействие измерительного прибора не позволяет точно определить эти значения. Такое толкование является совершенно неправильным.” ⁴


И чуть дальше:

“Согласно Борну квадрат модуля волновой функции определяет вероятность dP того, что частица будет обнаружена в объеме dV:


. (14.2)


Интеграл от выражения (14.2), взятый по всему пространству, должен равняться единице:


. (14.3)


Действительно, этот интеграл дает вероятность того, что частица находится в одной из точек пространства, которая равна единице.” ⁵


Как совместить утверждение, что частица с вероятностью, равной единице, находится в одной из точек пространства (вторая цитата), и что частица не может иметь точных координат (первая цитата)? Или частица как-то может находиться в некоторой точке пространства без точных координат?


У Фейнмана, разумеется, столь противоречивых утверждений на соседних страницах нет. Но и в его изложении проблемы порой встречаются слова странные, которые скорее запутывают читателя, чем помогают что-нибудь понять. По поводу пулеметной стрельбы по щели он пишет:


“Если движение всего вещества, подобно электронам, нужно описывать, пользуясь волновыми понятиями, то как быть в нашем первом опыте? Почему мы не увидели там интерференционной картины? Дело, оказывается, в том, что у пуль длина волны столь незначительна, что интерференционные полосы становятся очень тонкими. Столь тонкими, что никакой детектор разумных размеров не разделит их на отдельные максимумы и минимумы.” ⁶


Неужели Фейнман всерьез думает и предлагает думать нам, что рикошетирование пуль на краях щели хоть как-то связано с интерференцией? И почему “движение всего вещества ... нужно описывать, пользуясь волновыми понятиями”?


Мы уже говорили о том, что Y-функция по мнению Фейнмана не может быть связана с какой-то реальностью. Более элегантно выражается по этому поводу Гейзенберг (цитата приводится Вайскопфом ⁷):


«Концепция объективной реальности элементарных частиц, следовательно, курьезным образом испаряется, обращаясь не в туман, не в какое-то новое неясное или еще не постигнутое понятие реальности, а в прозрачную ясность математики, которая теперь соответствует не поведению атомных частиц, а, скорее, нашим знаниям об этом поведении.»


И В.Вайскопф возражает против такой концепции тоже весьма элегантно:


“Я не согласен с заявлением о том, что в атомном мире существует какой-то недостаток реальности. В конце концов, видимый реальный мир состоит из тех же самых атомов, обнаруживающих такое странное поведение. Действительно, атомный мир отличается от нашего привычного мира сильнее, чем когда-то ожидали; он обладает более богатым набором явлений, чем можно вообразить, пользуясь классическими представлениями. Но все это не делает его менее реальным.” ⁸


И еще несколько слов о том, как, скажем так, небрежное объяснение затрудняет понимание существа дела. Как выяснилось, электрон обладает спином - собственным моментом импульса. И по поводу невозможности объяснения существования этого последнего в рамках классической физики приводится обычно такое обоснование.

Магнитный момент электрона, который “вращается” по орбите, связывается с механическим моментом M (мы изменили принятое нами ранее обозначение для момента импульса) соотношением


.


Однако, для спиновых моментов


“... отношение собственных магнитного и механического моментов в два раза больше, чем для орбитальных моментов:


. (31.2)


Таким образом, представление об электроне как о вращающемся шарике оказалось несостоятельным.” ⁹


Конечно, отношение к написанному в книжках должно быть уважительным, но не обязательно все написанное принимать на веру. Вот и эта “трудность” с вдвое большим отношением моментов, если немного подумать, может быть легко преодолена.

Представим себе электрон в виде заряженной сферы очень маленького радиуса и пусть масса этой сферы ровно в два раза меньше массы электрона. Другая половина массы будет приходиться на электрическое поле, от электрона, естественно, неотделимое.

Подсчитаем энергию поля и приравняем ее половине массы электрона: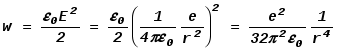


;

;

.


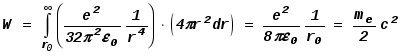Эта величина приводится в справочниках как “классический радиус электрона”. Если предположить, что это и есть радиус нашей заряженной вращающейся сферы, то, поскольку при ее вращении электрическое поле не вращается, а удельный заряд сферы вдвое больше, чем у электрона (масса в два раза меньше), мы как раз и получим нужное нам отношение .


Я ни в коем случае не предлагаю Вам представлять себе электрон в виде “вращающегося маленького шарика”! Я просто хочу обратить внимание на неправомочность утверждения “оказалось несостоятельным”.