Этот документ использован в разделе "Про электронику и схемотехнику"

Рассмотренный в предыдущем разделе процесс зарядки конденсатора посредством перенесения заряда с одной обкладки на другую имеет исключительно теоретический интерес, как метод расчета энергии конденсатора. Реально конденсаторы заряжают, подключая их к источнику ЭДС, например, к гальванической батарее.

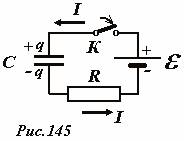
Пусть конденсатор емкостью C подключен к источнику, ЭДС которого равна ? (Рис. 145). Полное электрическое сопротивление цепи (включающее и внутренне сопротивление источника) обозначим R. При замыкании ключа в цепи пойдет электрический ток, благодаря которому на зарядках конденсатора будет накапливаться электрический заряд. По закону Ома сумма напряжений на конденсаторе 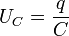и резисторе U_R = IR равна ЭДС источника 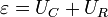, что приводит к уравнению

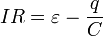. (1)

В этом уравнении заряд конденсатора и сила тока зависят от времени. Скорость изменения заряда конденсатора по определению равна силе тока в цепи 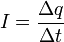, что позволяет получить уравнение, описывающее изменение заряда конденсатора с течением времени

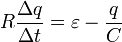. (2)

Можно также получить уравнение, непосредственно описывающее изменение силы тока в цепи с течением времени. Для этого на основании уравнения (1) запишем уравнения для малых изменений входящих величин

.

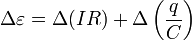Формально эту операцию можно описать следующим образом: уравнение (1) следует записать для двух моментов времени t и (t + ?t), а затем из второго уравнения вычесть первое. Так как ЭДС источника постоянна, то ее изменение равно нулю ?? = 0, сопротивление цепи и емкость конденсатора постоянны, поэтому их можно вынести из под знака изменения ? , поэтому полученное уравнение приобретает вид

.

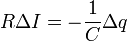Наконец разделим его на промежуток времени, в течение которого произошли эти изменения, в результате получаем искомое уравнение (с учетом связи между силой тока и изменения заряда)

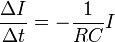. (3)

Математическая смысл этого уравнения указывает, что скорость уменьшения тока пропорциональна самой силе тока. Для однозначного решения этого уравнения необходимо задать начальное условие – значение силы тока в начальный момент времени I₀ = I(0).

С уравнениями такого типа мы познакомились в «математическом отступлении», поэтому здесь его анализ проведем кратко. В начальный момент времени, когда заряд конденсатора равен нулю, скорость возрастания заряда (то есть сила тока) максимальна и равна 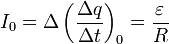. Затем по мере накопления заряда сила тока будет уменьшаться, когда напряжение на конденсаторе станет равным ЭДС источника, заряд конденсатора достигнет максимального стационарного значения 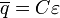и ток в цепи прекратится.

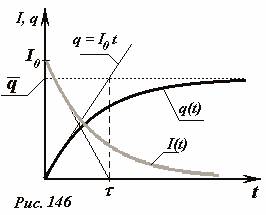
Схематически зависимости заряда конденсатора и силы тока в цепи от времени показаны на рис. 146. Для оценки времени зарядки конденсатора можно принять, что заряд возрастает до максимального значения с постоянной скоростью, равной силе тока в начальный момент времени. В этом случае

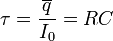. (4)

Аналогичная оценка исчезновения тока, полученная на основании уравнения (3) приводит к этому же результату.

Строго говоря, время зарядки конденсатора, описываемой уравнением (2) равно бесконечности. Это парадокс можно исключить, если принять во внимание дискретность электрического заряда. Кроме того, заряд конденсатора, подключенного к батарее с течением времени случайным образом изменяется, флуктуирует, поэтому рассматриваемое уравнение описывает некоторые усредненные характеристики процесса. Тем не менее, полученная оценка времени RC широко применяется в приближенных расчетах, часто ее называют просто временем зарядки конденсатора.

Рассмотрим теперь превращения различных форм энергии в данном процессе. Понятно, что причиной тока в цепи и как следствие зарядки конденсатора являются сторонние силы источника. На первый взгляд, энергетический баланс включает определенное противоречие: если источник сообщил конденсатору заряд q, то сторонние силы совершили при этом работу A₀ = q? , при этом энергия конденсатора стала равной 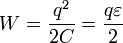, что в два раза меньше работы совершенной источником. Противоречие исчезает, если принять во внимание, что в процессе зарядки по цепи течет электрический ток, поэтому на резисторе выделяется некоторое количество теплоты, то есть часть энергии источника переходит в тепловую. Мысленно разобьем время зарядки на малые промежутки ?t_i (i = 1,2,3...). Перепишем уравнение (1) в виде

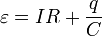, (5)

и умножим его на величину малой порции заряда, переносимого за малый промежуток времени ?t_i, ?q_i = I_i?t_i . В результате получим

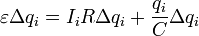. (6)

Здесь обозначено q_i - заряд конденсатора перед перенесением рассматриваемой порции заряда. Каждый член полученного уравнения имеет явный физический смысл:

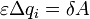- работа сторонних сил по перемещению порции заряда ?q_i;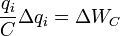

- увеличение энергии конденсатора при увеличении его заряда на ?q_i;

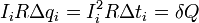- количество теплоты, выделившееся на резисторе, при протекании

порции заряда ?q_i.

Таким образом, закон сохранения энергии, выражаемый уравнением баланса (6) для малого промежутка времени оказывается выполненным, следовательно, он будет выполнен и для всего процесса зарядки. Просуммируем выражение (5) по всем промежуткам времени зарядки, в результате чего получим:

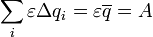- полная работа сторонних сил по перенесению электрического заряда, равного стационарному заряду конденсатора;

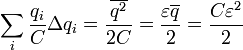- энергия заряженного конденсатора;

наконец, 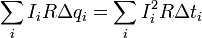- количество выделившейся на резисторе теплоты.

Принимая во внимание уравнение (3) и формулы из «математического отступления», последнюю сумму можно выразить в виде

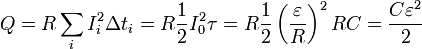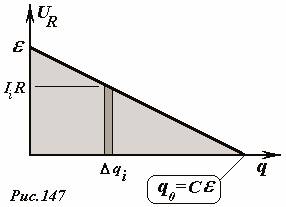
. (6)

Эта сумма же может быть вычислена графически. Формула (1) задает зависимость напряжения на резисторе U_R = IR от заряда конденсатора. Эта зависимость линейна, ее график (Рис. 147) является отрезком прямой линии. За малый промежуток времени через резистор протечет малый заряд ?q_i, при этом выделится количество теплоты 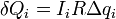, которое численно равно площади узкой полоски, выделенной на рисунке. Полное количество теплоты, выделившейся при прохождении всего заряда численно равно площади треугольника под графиком зависимости U_R(q), то есть

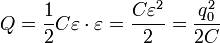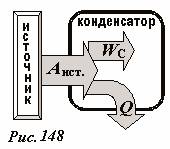
. (7)

Таким образом, энергетический баланс полностью сходится и для всего процесса целиком: работа, совершенная источником равна сумме энергии конденсатора и количества выделившейся теплоты A = W_C + Q. Схематически преобразование энергии в этом процессе показано на рис. 148.

Интересно заметить, что количество теплоты, выделяющееся при зарядке, не зависит о сопротивления цепи и в точности равно энергии конденсатора. То есть, половина энергии источника переходит в энергию электрического поля, а вторая в тепловую энергию, выделяющуюся в цепи: природа требует своеобразный пятидесятипроцентный налог в виде тепловых потерь, не зависимо от сопротивления цепи и емкости конденсатора^[1].

Примечания

1. ^ Но эти параметры цепи определяют время процесса.