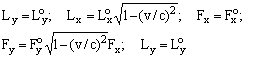Международный Конгресс - 2000
ФУНДАМЕНТАЛЬНЫЕ ПРОБЛЕМЫ ЕСТЕСТВОЗНАНИЯ И ТЕХНИКИ
С.-Петербург, Университет
2 - 8 июля 2000 г.
Доклад
КРИЗИС РЕЛЯТИВИСТСКИХ ТЕОРИЙ
Кулигин В.А., Кулигина Г.А., Корнева М.В.
Физический факультет, Воронежский госунивестет
Университетская пл. 1, Воронеж, 394693, РОССИЯ
E-mail: kuligin@ el.main.vsu.ru
ПРЕДИСЛОВИЕ.
С самого своего возникновения и по настоящее время Специальная теория относительности подвергалась справедливой критике. Аргументов, предлагаемых критиками, было достаточно, чтобы давно признать Специальную теорию относительности несостоятельной как с точки зрения логики, так и с экспериментальной точки зрения. Тем не менее, эта теория рассматривается как научная теория и в настоящее время. Главная причина подобной устойчивости - догматизм, господствующий в современной физике. В большинстве случаев апологеты эту критику игнорировали и замалчивали.
Международный Конгресс-2000 подтолкнул нас подвести промежуточные итоги наших исследований. Мы собрали все наши критические результаты в общий доклад "Кризис релятивистских теорий". Он включает в себя следующие разделы (части):
1. Анализ теории относительности.
2. Анализ основ электродинамики.
3. Причинность в физике.
4. Вариационный принцип релятивистских теорий.
5. Электромагнитная масса.
6. Магнитные взаимодействия движущихся зарядов.
Благодаря проведенному анализу, можно достоверно утверждать, что релятивистские теории не являются научными теориями из-за большого количества математических, физических и гносеологических ошибок. Эти теории должны быть подвергнуты пересмотру. Однако, прежде должна быть пересмотрена философия естествознания из-за большого числа гносеологических ошибок в физических теориях.
КРИЗИС РЕЛЯТИВИСТСКИХ ТЕОРИЙ
Часть1. Анализ теории относительности.
Кулигин В.А., Кулигина Г.А., Корнева М.В.
Физический факультет, Воронежский госунивестет
Университетская пл. 1, Воронеж, 394693, РОССИЯ
E-mail: kuligin@ el.main.vsu.ru
Дан анализ сущности преобразования Лоренца показал следующее. Все инерциальные системы имеют единое время. Все инерциальные системы имеют общее пространство. Специальная теория относительности не может рассматриваться как научная теория.
Kuligin V.A., Kuligina G.A., Korneva M.V. The analysis of Lorentz's transformation shown the following. All inertial frames have total time. All inertial frames have common space. The Special Relativity theory cannot be considered as a scientific theory.
Введение.
История науки (в частности, кризис физики на рубеже 19 - 20 веков) свидетельствуют о пагубном влиянии гносеологических ошибок в естествознании и других областях знания на мировоззрение, на формирование социально-экономических отношений и на сами науки. Дело в том, что подрываются основы материалистического мировоззрения и открываются пути идеализму и агностицизму. Вследствие этого гносеологические ошибки приводят к неправомерным интерпретациям естественнонаучных фактов и закономерностей, а потому толкают ученых на проведение исследований в заведомо тупиковых направлениях, на выдвижение ошибочных гипотез. Естествознание обрекается на застой в области фундаментальных исследований, на бесплодную растрату сил, времени средств.
В силу этого важное значение приобретает анализ естественнонаучных теорий фундаментального характера с позиции теории познания объективной истины с целью выявления гносеологических ошибок, а также сочетание гносеологического анализа с научным анализом для устранения гносеологических ошибок в фундаментальных теориях.
К числу причин, порождающих гносеологические ошибки, можно отнести:
а) незнание частью исследователей содержания философских категорий и их взаимной связи;
б) неумение сопоставить частно-научные категории с философскими и, как следствие, провести гносеологический анализ.
Целью настоящей работы является гносеологический анализ сущности преобразования Лоренца и выявление противоречий между выводами теории познания объективной истины и интерпретацией пространственно-временных отношений в специальной теории относительности. Мы будем условно считать, что преобразование Лоренца объективно отражает количественную сторону явлений. Нас будет интересовать только интерпретация явлений (как отражений сущности) и сама сущность преобразования в рамках преобразования Лоренца. Напомним, что Специальная теория относительности есть, по существу, интерпретация этого преобразования, предложенная А.Эйнштейном.
1.Явление и сущность.
Коль скоро целью нашей работы является установление сущности преобразования Лоренца с позиции теории познания объективной истины, нам необходимо познакомиться с философскими категориями "явление" и "сущность" и выявить между ними взаимную связь. Обратимся к истории науки. В 1543 г. выходит известная книга Н.Коперника "Об обращении небесных сфер", с появлением которой, по словам Ф.Энгельса, начинает свое летоисчисление освобождение естествознания от теологии. В чем же, однако, преимущество гелиоцентрической системы Коперника перед геоцентрической системой Птолемея? Вопрос этот далеко не праздный.
Во-первых, в то время точность обеих систем практически не отличалась друг от друга. Максимальное расхождение предсказаний составляло не более 0.5°. Экспериментальные исследования астрономов (астрономические наблюдения) не могли внести ясность, поскольку точность и той, и другой системы могла быть повышена путем ее уточнения и усложнения.
Во вторых, иногда в качестве решающего аргумента приводят принцип простоты и наглядности: система Коперника, по мнению ряда исследователей, выглядит "проще", чем система Птолемея. Простота - понятие субъективное. Во времена Коперника его система могла казаться сложной, искусственной, фантастической. Действительно, Земля видится человеку плоской, очерченной линией горизонта. Поэтому в представлениях того времени Земля напоминала блин, покоящийся на слонах, китах, черепахах. Представление о сферической форме Земли казалось абсурдом, нелепицей и не согласовывалось с житейскими представлениями. Как с точки зрения современника Коперника могла такая большая Земля повиснуть "ни на чем" и вращаться вокруг "маленького" Солнца? Видимо дело не только и не столько в "простоте", а в чем-то более глубоком и существенном. Недаром, несмотря на гнет теологических предрассудков, система Коперника смогла выстоять и обрести право на жизнь. Однако для этого потребовалось время и борьба исследователей. Путь познания истины никогда не был простым.
В третьих, следует отметить еще одно немаловажное обстоятельство. Обе системы (Коперника и Птолемея) отражали и отражают объективные явления материального мира. Современная наука, отказавшись от птолемеевской системы, не отказалась от птолемеевского подхода для описания видимого движения планет на небесной сфере.
Итак, что же заставило ученых отказаться от системы Птолемея? Ответ с позиций современной теории познания мы видим в следующем. Система Птолемея (хорошо или плохо - не столь принципиально) описывала движение планет, видимое с Земли, т.е. описывала явление. Если же мы оказались, например, на Меркурии или Марсе, то земную птолемеевскую систему нам пришлось бы упразднить и заменить новой.
Система Коперника сумела схватить сущность взаимного движения планет солнечной системы. Такое описание, говоря современным языком, уже не зависело от того, какую планету в качестве системы отсчета захочет выбрать себе наблюдатель.
С точки зрения теории познания объективной истины теологи совершали грубейшую ошибку: они сущность подменяли явлением. Наблюдаемое с Земли движение планет по небосводу они считали их действительным движением относительно Земли.
Гносеологические ошибки, связанные с отождествлением явления и сущности, с подменой сущности явлением, с истолкованием явления как сущности, существуют, как это ни парадоксально, и в настоящее время. Это, несмотря на то, что от Коперника нас отделяют столетия. И вот что закономерно, для защиты ошибочных представлений, связанных с истолкованием явления как сущности, человеческий разум всегда прибегает к домыслам, нагромождению вспомогательных гипотез, мистике и т.д. Однако современные "слоны" и "черепахи", как и во времена Коперника, отнюдь не будут выглядеть монстрами в современной картине мира. Они будут иметь вполне "респектабельный" вид, соответствующий духу времени и сложившемуся стилю мышления. Вот почему нам сейчас важно установить те признаки, которые позволили бы нам отличить сущность от явления, а явление от сущности.
2. Критерии отличия.
В течение многих десятилетий в среде физиков сформировалось негативное отношение к философским исследованиям, касающимся фундаментальных наук. Возникло устойчивое мнение о "бесплодности" и "ненужности" философских исследований. Полностью разделяя справедливое чувство неудовлетворенности современным состоянием философской мысли, мы не склонны "выплескивать ребенка вместе с пеной".
На примере анализа сущности преобразования Лоренца мы намерены показать важную роль теории познания объективной истины в фундаментальных исследованиях. Роль эта заключается в том, что теория познания не только помогает в поиске объективной истины, но без нее невозможно установление и обоснование характера найденной истины (объективная истина, субъективная истина или заблуждение).
Возвращаясь к явлению и сущности, отметим, что вопрос о взаимной связи, этих понятий и их отличительных признаках в философской литературе обсуждался неоднократно. Однако такие исследования носят схоластический, поверхностный характер и мало пригодны для анализа физических концепций и научных теорий, хотя они опираются на исторический анализ и содержат немало интересных примеров. Следовательно, вопрос о признаках, которые позволяют отличить сущность от явления, нам придется анализировать самостоятельно.
"Сущность является; явление существенно". Это философское положение нам необходимо конкретизировать. Обратимся к примеру. Рассмотрим сферический предмет, вплавленный в стеклянную пластину. При наблюдении нам будет казаться, что шарик имеет не сферическую, а эллипсоидальную форму. Это и есть явление.
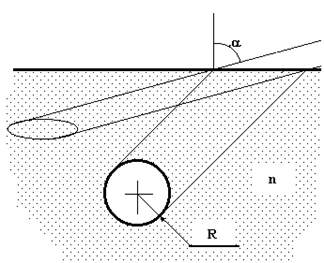
Рис.1.
Изменяя угол наблюдения α, мы будем видеть различную величину "сплюснутости" шарика. Угол наблюдения α и коэффициент преломления стекла n это условия, при фиксации которых мы будем наблюдать объективное явление. Каждому условию соответствует свое объективное явление, которое в чем-то будет отличаться от других явлений, соответствующих другим условиям. Изменяется условие - изменяется явление, но сам объект не испытывает никаких изменений. Собственная форма объекта - сфера - выступает по отношению к совокупности явлений одной из характеристик сущности. Очевидно, что по одному явлению познать сущность не представляется возможным. Сущность познается по совокупности явлений, принадлежащих заданному классу условий.
С позиции теории познания любое явление из заданной совокупности представляет собой сочетание особенного (характерного только для данного явления и отличающего данное явление от остальных явлений совокупности) и общего (т.е. того, что остается неизменным, инвариантным для всех явлений совокупности, принадлежащих взятому классу условий).
Познание сущности идет от явлений, путем отсечения второстепенного, особенного, к выделению общего, т.е. того, что остается неизменным для всех явлений данной совокупности. Сущность как общее для всех явлений отражает глубинные связи и отношения. Процесс поиска сущности сложен и нет каких-либо рецептов для прямого перехода от явлений к сущ-
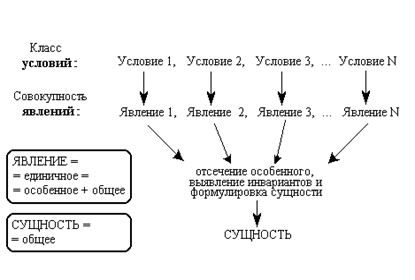
Рис. 2.
ности. Однако приведенный анализ позволяет сформулировать весьма полезное правило:
ЯВЛЕНИЕ ЗАВИСИТ
ОТ УСЛОВИЙ ЕГО НАБЛЮДЕНИЯ.
СУЩНОСТЬ ОТ ЭТХ УСЛОВИЙ НЕ ЗАВИСИТ.
Конечно, проблема связи условия, явления и сущности этими правилами не исчерпывается. Условия могут быть различными: существенными и несущественными. Сущность в полном объеме (как абсолютную истину) по одной совокупности явлений познать невозможно. Поэтому говорят о "срезах" сущности, о сущностях первого, второго и других порядков.
Явление можно наблюдать, измерять фотографировать. В этом смысле выражения: "нам будет казаться", мы будем измерять", "мы будем фотографировать" и т.п. будут равнозначными в том смысле, что принадлежат процессу регистрации явления. В слове "кажется" нет никакой иллюзии, мистики, а есть отношение к сущности. Однако и сущность как инвариантное представление может быть охарактеризована некоторыми инвариантными параметрами и характеристикам (например, радиус сферы в рассмотренном выше примере). Эти характеристики мы будем именовать инвариантными проявлениями сущности. Здесь мы можем уточнить процесс познания сущности.
Этот процесс предусматривает выделение инвариантных характеристик (инвариантных проявлений сущности), на базе которых идет процесс осмысления и формулировки сущности. Из проведенного анализа вытекает, что поиск симметрий и инвариантов в физике имеет под собой глубокое основание. Инварианты и симметрии в физических теориях выступают как инвариантные проявления сущности. Опираясь на них, следует отыскивать сущность явлений.
"Сущность является". Кому же должна являться сущность в форме явления? Кто должен наблюдать, измерять, регистрировать явление и его характеристики? Естественно, это должен делать прибор, реальный, или идеальный наблюдатель. При описании явлений невозможно обойтись без наблюдателя, без задания условий наблюдения, без задания систем отсчета.
3.Трактовка явлений и теория познания.
В рамках специальной теории относительности существуют явления, интерпретация которых наталкивается на определенные трудности логического характера. К таким явлениям относятся:
а) "замедление" времени,
б) "сжатие" масштаба вдоль вектора скорости относительного движения двух инерциальных систем отсчета. Условием наблюдения явлений в рамках специальной теории относительности является величина скорости относительного движения двух инерциальных систем отсчета. Поскольку упомянутые выше эффекты зависят от этой скорости, т.е. от условия, они действительно представляют собой явления, которые можно измерять, наблюдать, фотографировать и т.д. За этими явлениями скрыта некая сущность, которую нам еще предстоит установить.
Рассмотрим парадокс времени. Пусть имеются две инерциальные системы отсчета К и К', снабженные наблюдателями, движущиеся друг относительно друга со скоростью v. Наблюдатель системы К обнаружит, что его часы идут быстрее, чем часы у наблюдателя в К'. Но инерциальные системы равноправны. Поэтому наблюдатель системы K', сравнив показания часов, станет утверждать обратное: его часы идут быстрее, чем часы наблюдателя системы К.
И тот, и другой излагают объективные факты. Следовательно, между суждениями двух наблюдателей имеется логическое противоречие, которое легло в основу парадокса времени. Как разрешить парадокс? В какой системе отсчета время течет быстрее? Как время течет на "самом деле"? Процитируем точку зрения, которая нашла широкое распространение среди интерпретаторов основ специальной теории относительности [I] (см. стр. 203 - 204):
"Естественно, возникают два вопроса: во-первых, почему до появления теории относительности вся совокупность имевшихся фактов находилась в согласии с ньютоновскими представлениями об абсолютном характере длины тела и о едином мировом времени и, во вторых, являются ли сокращение размеров движущихся тел и замедление движущихся часов реальными или кажущимися ...
...Переходя ко второму вопросу, следует подчеркнуть, что весьма распространенные формулировки "кажущееся сокращение масштабов" и "кажущееся замедление хода часов" являются неудачными. Обычно авторы стремятся термином "кажущееся" подчеркнуть чисто кинематический характер сокращения. Вместе с тем, сокращение масштаба и замедление хода часов представляют реальный и объективный факт, отнюдь не связанный с какими-либо иллюзиями наблюдателя. Само собой разумеется, что все значения длины данного масштаба или промежутка времени, полученные в различных системах отсчета, являются равноправными. Все они "правильные". Трудность понимания этих утверждений связана исключительно с нашей привычкой считать понятия длины и промежутка времени абсолютными понятиями, когда в действительности они суть понятия относительные. Поэтому такие бессмысленно спрашивать какая длина является истинной, а какая - кажущаяся, как бессмысленно говорить "в действительности данное тело движется (или покоится)". Понятие длины и промежутка времени столь же относительны, как и понятия движения и покоя".
Продемонстрированный выше подход не выдерживает критики с точки зрения теории познания, поскольку автор не понимает, что за обыденными словами "кажущееся" и "истинное" стоят философские категории "явление" и "сущность". Действительно, длины одного и того же отрезка, измеренные в разных инерциальных системах отсчета, вообще говоря, различны. Они никак не могут быть "равноправными". Их не инвариантность по отношению к выбору инерциальной системы отсчета свидетельствует о том, что мы имеем дело с явлениями, за которыми стоит сущность. Именно поэтому отнюдь не "бессмысленно" спрашивать: "какая длина является истинной, а какая - кажущейся"? На этот вопрос можно ответить лишь тогда, когда ясна сущность этих явлений.
Однако о сущности у автора не сказано ни слова. Поэтому замечание об "относительности длин и промежутков времени" нацелено не на разъяснения природы явлений и не на разрешение логических противоречий типа парадокса времени, а на их сохранение, "узаконивание" в физической теории. Этим распространенным стремлением "оправдать" наличие логических противоречий в теории, а не разрешить их, как раз и объясняется "трудность понимания" современного истолкования явлений в специальной теории относительности. Известный ученый Бриджмен так писал о "равноправии " интервалов времени и длин масштабов, измеренных в различных инерциальных системах отсчета (цит. по [2]): "было бы жестоко снабжать физиков резиновыми линейкам и исключительно неправильно идущими часами". Можно не принимать операционализм Бриджмена, но с данным остроумным замечанием нельзя не согласиться.
"Сокращение" масштаба и "растяжение" времени - объективные явления. Поэтому, когда мы регистрируем явления, мы обязаны задать вопрос: а что происходит "на самом деле", какова сущность наблюдаемых явлений?
Приведем пример еще одного интерпретатора "замедления" времени (см. [3] , стр. 71):
"Формула ![]() в этом случае просто
показывает, что промежуток собственного времени тела между событиями, происшедшими
с телом или на теле, всегда меньше промежутка времени между этими событиями,
отсчитанными по часам любой ИСО, относительно которой тело движется. Не следует
забывать при этом, что собственный промежуток времени отсчитывается одними
часами, а промежуток времени в системе, относительно которой тело движется, -
по крайней мере, двумя. Это очень существенно, потому что часто говорят; что движущиеся
часы идут медленнее неподвижных. Нельзя не признать ату фразеологию крайне
неудачной, дело в том, что часы всех ИСО идут совершенно одинаково, различным
оказывается отсчет промежутков времени между событиями. Но это естественно,
поскольку часы, синхронизированные в одной ИСО, оказываются
рассинхронизированными в другой".
в этом случае просто
показывает, что промежуток собственного времени тела между событиями, происшедшими
с телом или на теле, всегда меньше промежутка времени между этими событиями,
отсчитанными по часам любой ИСО, относительно которой тело движется. Не следует
забывать при этом, что собственный промежуток времени отсчитывается одними
часами, а промежуток времени в системе, относительно которой тело движется, -
по крайней мере, двумя. Это очень существенно, потому что часто говорят; что движущиеся
часы идут медленнее неподвижных. Нельзя не признать ату фразеологию крайне
неудачной, дело в том, что часы всех ИСО идут совершенно одинаково, различным
оказывается отсчет промежутков времени между событиями. Но это естественно,
поскольку часы, синхронизированные в одной ИСО, оказываются
рассинхронизированными в другой".
Так как же все-таки идут эти "злополучные " часы: "синхронно" (одинаково) или рассинхронизированы (идут по-разному)? Автор бросается из крайности в крайность, то, объявляя "фразеологию крайне неудачной", а часы "синхронными", то, объявляя часы "рассинхронизированными". Конечно, можно все это объяснение принять на веру, но логического противоречия в парадоксе времени это объяснение разрешить не может. Вот почему часто интерпретаторы называют вопрос: "а что мы имеем на самом деле"? - "бессмысленным". Такие вопросы загоняют их в тупик.
4. Пространство и время в преобразовании Лоренца.
Чтобы проиллюстрировать единство времени в различных ИСО, обратимся к рис. 3, на котором представлено взаимное расположение наблюдателей в сопоставляемых системах отсчета А и В. В каждой из систем имеется генератор, задающий световые сигналы через равные промежутки времени Т, и наблюдатель, регистрирующий временные интервалы между импульсами (вспышками).
Будем считать, что при относительной скорости инерциальных систем А и В, равной нулю, выполняется условие ТА = TВ = Т'A = Т'B. Рассмотрим теперь случай, когда относительная скорость движения инерциальных систем А и В отлична от нуля. Очевидно, что значения интервалов ТA и ТB не изменятся, т.к. это характеристики сущности. Иными словами, наблюдатели не увидят изменения частоты собственного генератора. Преобразование Лоренца это линейное алгебраическое преобразование. Оно устанавливает взаимно-однозначную связь между точками xi системы К и точками x'i системы К'. Эта связь не зависит от способа перехода наблюдателя из К в К' и обратно. [1]
ТА и TВ - интервалы времени, измеренные в собственных ИСО, являющиеся характеристиками сущности; Т'A и Т'B - интервалы времени, наблюдаемые их "чужих" систем (явления).
Рис. 3.
Изменятся наблюдаемые "чужие" интервалы времени Т'A и Т'B (явления). В соответствии с преобразованием Лоренца будем иметь:
I) ТA< Т'B (система А), 2) TB < T'A (система В).
Для полного определения логической связи между 4-мя величинами (ТА ; TВ ; Т'A ; Т'B) двух записанных нами неравенств недостаточно. Необходимы еще два условия.
А.Эйнштейн предложил считать, что Т'A есть собственное время системы А, т.е.ТА, а Т'B есть собственное время системы В, т.е. ТВ. Эта связь не зависит от инерциальной системы отсчета.
3) Т'A= ТA 4) T'B =TB
Так Эйнштейн подошел к своему пониманию и объяснению физического смысла преобразования Лоренца. Очевидно, что система из четырех соотношений оказалась логически противоречивой. Выражения 1) и 2) примут вид:
I) ТA< ТB , 2) TB < TA .
Гносеологический анализ, проведенный в [4], [5], показал, что Эйнштейн подобно Птолемею допустил типичную гносеологическую сшибку. Наблюдаемое явление (Т'A и Т'В )он истолковал как сущность (ТA и ТВ). Ошибочное истолкование породило ряд логических противоречий, например, парадокс близнецов и другие. То же самое можно сказать и об интерпретации "сжатия" масштаба.
Единственно возможным вариантом, который не противоречит равноправию инерциальных систем отсчета и логике, является вариант, опирающийся на соотношения:
1) ТА < Т'A; 2)TВ <Т'B; 3) Т'A= Т'B; 4) ТА= TВ
Смысл его очевиден. Собственное время во всех инерциальных системах отсчета едино, т.е. течет в одном ритме, темпе (ТА= TВ). Явления обладают симметрией (Т'A= Т'B; ТА< Т'A; TВ < T'B). Это и есть реализация принципа равноправия инерциальных систем отсчета.
Именно здесь выявляется различие между эйнштейновской и новой интерпретациями сущности преобразования Лоренца.
а) Эйнштейновский (= птолемеевский) подход. Замедление времени, которое мы наблюдаем (явление), есть "действительное" замедление времени. Время в движущейся системе отсчета действительно течет медленнее, чем в неподвижной (сущность).
б) Материалистический (= коперниканский) подход. Замедление времени есть объективное явление, которое мы наблюдаем и регистрируем в нашей инерциальной системе. Однако в самой движущейся системе время течет в том же темпе (сущность), что и в неподвижной. Кажущееся замедление времени обусловлено свойствами преобразования Лоренца.
Итак, мы видим повторение Эйнштейном типичной гносеологической ошибки, которую задолго до него совершил Птолемей: придание объективному явлению статуса сущности.
Гносеологический анализ сущности преобразования Лоренца [4] позволил выявить ряд интересных закономерностей. Как оказалось, сущность преобразования Лоренца заключается в отображении процессов и их характеристик из одной инерциальной системы отсчета в другую в форме явлений. Все параметры и характеристики, полученные с помощью преобразования Лоренца, относятся к разряду явлений и не всегда совпадают с действительными параметрами и характеристиками, измеренными в системе отсчета, связанной с исследуемым объектом. Однако при преобразовании Лоренца некоторые величины остаются неизменными (инвариантными). Среди них:
1. Сохраняется действительное равноправие всех инерциальных систем отсчета. Для краткости будем их именовать ИСО.
2. Физическое время остается общим и единым для всех ИСО. Это единое мировое время.
3. Общим для всех ИСО остается трехмерное пространство.
4. Скорость света и сечение светового луча остаются неизменными (инвариантными) для всех ИСО.
Наблюдаемые "замедление" времени и "сжатие" масштаба - суть объективные явления, т.е. искаженные отображения истинного темпа времени (единого для всех ИСО) и масштаба координатной оси (общего для всех ИСО).
Уже сам принцип равноправия инерциальных систем предполагает, например, единство времени во всех ИСО. В противном случае различие в темпах изменения времени могло бы служить критерием для дифференциации различных ИСО.
5. Фотоаппарат и объективность.
Теперь мы знаем, что пространство является общим для всех инерциальных систем отсчета, а наблюдаемые искажения связаны с относительным движением наблюдателя и исследуемого объекта. Они - суть явления. Кажущееся искажение объемных объектов связано с искажением фронта световой волны. Оно рассмотрено в [4]. Переход наблюдателя из одной системы отсчета в другую не влияет ни на материальные объекты, ни на скорость течения процессов в какой бы инерциальной системе отсчета наблюдатель ни находился.
Примечательно, что проблема сопоставления длин пространственных отрезков наталкивается на те же логические трудности, что и проблема сравнения интервалов времени (парадокс близнецов). Выше мы цитировали точки зрения двух физиков. Теперь для справедливости мы процитируем философа, посвятившего свою жизнь теории относительности. Он не лучше и не хуже других философов. Обратимся к работе [6], в которой объясняется "относительность длин отрезков" в специальной теории относительности. Сравниваются длины двух поездов П1 и П2. Суть легко выявляется из рис. 4.

система отсчета П 1 система отсчета "шар" система отсчета П 2
Рис. 4.
На странице 97 читаем:
"Итак, по отношению к поезду П1 короче поезд П2, по отношению же к поезду П2 короче поезд П1. Какой же поезд "на самом деле" короче? Во всех трех случаях фиксируются объективные, независящие от наблюдателей факты. Машинист поезда П1 прав, потому, что по отношению к нему поезд П2 действительно короче. Это можно зафиксировать объективными методами при помощи приборов, например при фотографировании. Но машинист поезда П2 прав, потому, что по отношению к нему, поезд П1 на самом деле короче. Это можно зафиксировать фотоаппаратом или каким-либо другим прибором. Правы и мы, смотрящие с воздушного шара на поезда П1 и П2 и видящие, что длина их одинакова"
Мы привели эту цитату из [6], чтобы показать, что за этими "объективными, независящими от наблюдателей фактами" автор не видит своей субъективной роли. Ведь он сам выбрал себе в качестве системы отсчета воздушный шар. Он своему усмотрению он мог бы выбрать любую другую систему отсчета. К этому его никто не понуждал, даже "метафизики", которых он гневно клеймит в своей книге. Сравнивая результаты в трех инерциальных системах отсчета, он не хочет видеть свое субъективное участие в выборе условий проведения эксперимента, а потому не может понять, что все эти" факты" - суть явления, за которыми от него скрылась сущность. На протяжении всей своей монографии он доказывает, что достаточно сфотографировать материальный объект, используя объектив, и объективность у него "в кармане".
Такой, с позволения сказать, "философский анализ" имеет свое название - иллюстрационизм. Суть его в том, что философ на популярном уровне пересказывает содержание физической теории, обильно сдабривая пересказ банальными философскими истинами. Иллюстрационизм как метод нашел широкое использование в трудах по философии естествознания и справедливо вызывает негативное отношение физиков к подобным философским "исследованиям".
В отличие от иллюстрационизма и других "методов" современной философии материалистическая теория познания после 20-х годов практически не развивалась. В каталоге современной философской литературы нет ни одного учебника посвященного теории познания, ее целям и задачам, ее структуре, ее принципам, категориям и методам, границам применимости теории познания. Факт весьма прискорбный, если учесть, что какую бы конкретную предметную область мы ни познавали: историю или искусство, естественные науки или развитие общества - везде мы искали, ищем и будем искать объективную истину.
Теория познания естествознанию нужна не меньше, чем математика. Все эти вопросы очень важны, но выходят за рамки данной работы.
6. Наблюдаемая и истинная скорость объекта.
Теперь рассмотрим вопрос о наблюдаемой (явление) и истинной (характеристика сущности) скоростях частиц и их различии. Пусть мимо наблюдателя по прямой линии движется материальная точка со скоростью v. В собственной системе отсчета K' (ее координата x' постоянна) она дает световые вспышки через равные интервалы времени Δto. Эти вспышки регистрируются неподвижным наблюдателем в системе K. Мы можем мысленно представить прямолинейную траекторию, которая как бы разбита на равные отрезки длиной Δx светящимися точками. За время Δto система К успеет переместиться относительно K' на это расстояние Δx.
С помощью преобразования Лоренца найдем расстояние Δx между вспышками.
![]() (6.1)
(6.1)
где ΔТ это
наблюдаемое в системе К время между двумя вспышками, определенное с помощью
преобразования Лоренца ![]() .
.
Введем угол θ, образованный двумя векторами: вектором скорости v, направленным вдоль оси x, и вектором направления световых лучей от движущегося объекта к наблюдателю. Благодаря эффекту Доплера наблюдаемый интервал между световыми вспышками будет также зависеть от угла наблюдения θ. Учитывая искажение интервалов времени эффектом Доплера, найдем наблюдаемый интервал времени между вспышками, которые видны под углом θ в системе К. Он равен:
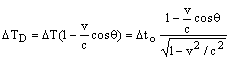 (6.2)
(6.2)
где ΔТD - наблюдаемый интервал времени между вспышками, искаженный эффектом Доплера; ΔТ- тот же интервал, когда инерциальные системы проходят мимо друг друга (θ=90о).
Теперь, выражая в (6.1) интервал Δto через ΔТD, получим:
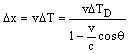 (6.3)
(6.3)
Отсюда нетрудно найти наблюдаемую (кажущуюся) скорость, которая зависит от угла наблюдения θ.
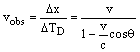 (6.4)
(6.4)
Когда θ=90о, т.е. когда генератор проходит мимо наблюдателя (как показано на рис. 3), мы имеем vobs=v (observed=наблюдаемый). Здесь наблюдаемая скорость совпадает с относительной скоростью движения инерциальных систем К' и К, которая входит в преобразование Лоренца. Итак, мы неожиданно обнаруживаем, что скорость v есть наблюдаемая (кажущаяся) скорость относительного движения инерциальных систем отсчета! Истинную скорость мы определим позже.
Полученный результат имеет интересные следствия. Во-первых, мы будем видеть неравномерное движение источника световых импульсов, скорость которого постоянно уменьшается. Наблюдаемое "ускорение" равно
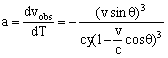 (6.5)
(6.5)
где у - координата движущейся точки.
Означает ли это, что на движущуюся частицу действуют некоторые силы? "Реальны" ли эти силы или же они "кажущиеся"? Как быть с принципом причинности? Ответ очевиден. Световые лучи, передавая информацию, искажают ее.
Замедление скорости имеет интересные следствия. Если v/c > 0.5, то при малых углах наблюдения θ наблюдаемая скорость движения объекта будет превышать скорость света в вакууме. Как это согласуется с постулатами Эйнштейна о существовании предельной скорости распространения взаимодействий?
Покажем принцип определения наблюдаемой скорости с точки зрения теории познания.
![]() (6.6)
(6.6)
В отличие от наблюдаемой скорости, в определение которой входит характеристика явления, истинную скорость (как инвариантную величину) мы должны определить как отношение двух инвариантных проявлений сущности. Она не должна зависеть от условий наблюдения v и θ.
Напомним, что длины отрезков, интервалы времени, времена жизни частиц, измеренные в их собственной системе отсчета, являются инвариантными проявлениями сущности (или кратко - "сущность"). Те же длины и интервалы времени, наблюдаемые из системы движущегося наблюдателя, будут явлениями. Они - суть отображение действительных значений, искаженные движением.
Истинная скорость V системе К определяется отношением двух "сущностей": реального пути, пройденного частицей в системе отсчета наблюдателя, к интервалу времени, единому для всех ИСО, за который этот путь пройден. Это инвариантный отрезок Δx и инвариантный интервал времени Δto.
![]() (6.7)
(6.7)
Истинная скорость (ее условно можно назвать "галилеевской") не зависит от условий наблюдения, т.е. от угла θ, постоянна и может превышать скорость света в вакууме. Нетрудно видеть, что истинная скорость V и кажущаяся скорость v, входящая в преобразование Лоренца, имеют связь:
![]() (6.8)
(6.8)
Мы можем записать матрицу Лоренца через истинную скорость V.
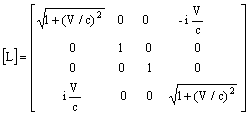 (6.9)
(6.9)
Эти результаты имеют интересное применение для объяснения появления у поверхности Земли μ-мезонов, рождающихся в верхних слоях атмосферы. Существующее объяснение использует следующую формулу.
![]() (6.10)
(6.10)
Скорость μ-мезона v не превышает скорости света. Расстояние, проходимое μ-мезоном, равно произведению наблюдаемой скорости v на наблюдаемое "время жизни" μ-мезонов ΔΤ. Это время жизни "удлиняется" для наблюдателя на Земле благодаря релятивистскому "замедлению времени".
Мы дадим другое объяснение, опирающееся на ту же формулу.
![]() (6.11)
(6.11)
Расстояние, проходимое μ-мезоном, равно произведению истинной скорости V на действительное "время жизни" μ-мезонов Δτ. При этом скорость μ-мезонов превышает скорость света в вакууме.
7. Парадокс диска.
Процитируем сначала отрывок из [7] (стр. 274):
"Здесь же полезно провести простое рассуждение, наглядно иллюстрирующее неизбежность возникновения неевклидовости пространства при переходе к неинерциальным системам отсчета. Рассмотрим две системы отсчета, из которых одна (К) инерциальна, а другая (К') равномерно вращается относительно К вокруг общей оси z, Окружность в плоскости x, y системы К (с центром в начале координат) может рассматриваться и как окружность в плоскости x', y' системы К'. Измеряя длину окружности и ее диаметр масштабной линейкой в системе К, мы получаем значения, отношение которых равно π, в соответствии с евклидовостью геометрии в инерциальной системе отсчета. Пусть теперь измерение проводится неподвижным относительно K' масштабом. Наблюдая за этим процессом из К, мы найдем, что масштаб, приложенный вдоль окружности, претерпевает Лоренцево сокращение, а радиально приложенный масштаб не меняется. Ясно поэтому, что отношение длины окружности к ее диаметру, полученное в результате такого измерения, оказывается больше π"
Здесь также сущность подменена явлением. Чтобы показать это, усовершенствуем описанный выше эксперимент. По краю диска с радиусом R расположим N = 100 лампочек. При неподвижном диске расстояние между ними равно:
![]() (7.1)
(7.1)
Примем это за масштаб. Пусть теперь диск вращается, а край диска имеет скорость v/c=0,15. Тогда наблюдаемое расстояние между лампочками (наблюдаемый масштаб) будет равно:
![]() (7.2)
(7.2)
Фотографируя диск, мы должны обнаружить на фотографии 101 лампочку.
![]() (7.3)
(7.3)
Итак, если Специальная теория относительности справедлива, тогда мы увидим на фотографии 101 лампочку. Можно ли, исходя из симметрии, указать какая лампочка "сфотографировалась" дважды?
Если же мы увидим на фотографии только 100 лампочек, тогда что именно предсказывает теория относительности: то, что должны наблюдать реально, или же мистику?
Заменим теперь лампочки одинаковыми зарядами и будем искать электромагнитное поле. Вновь проблемы. Каким числом зарядов будет создаваться это поле: N или N+1и почему? Будет ли справедлив закон сохранения заряда?
Преобразование Лоренца применимо только для связи двух инерциальных систем отсчета. Вектор скорости относительного движения этих систем должен быть неизменен. Однако на базе преобразования Лоренца строится механика движущихся частиц, траектории которых криволинейны. Для вычисления полей и потенциалов криволинейно движущегося заряда мы не имеем права использовать преобразование Лоренца. К каким "эффектам" приводит такое использование преобразования Лоренца, выходящее за границы применимости этого преобразования, мы уже знаем. Отсюда следует, что релятивистская механика, электронная теория Лоренца и электродинамика есть весьма сомнительные теории.
Заключение.
Итак, мы провели гносеологический анализ Специальной теории относительности, являющейся эйнштейновской интерпретацией преобразования Лоренца, и установили следующее.
1. Сущность преобразования Лоренца в том, что оно отображает действительные размеры материальных тел и скорость течения процессов во времени из одной инерциальной системы отсчета в другую в форме явлений. Ошибкой Эйнштейна было истолкование этих явлений как сущности, т.е. как действительных изменений, происходящих в движущейся системе отсчета.
2. В преобразовании Лоренца сохраняется действительное равноправие всех инерциальных систем отсчета.
3. Физическое время остается общим и единым для всех инерциальных систем. Это единое мировое время. Наблюдаемые искажения времени ("замедление времени") обусловлены поперечным эффектом Доплера (явление).
4. Общим для всех инерциальных систем остается трехмерное пространство. Наблюдаемые искажения формы пространственных объектов и пространственных отрезков, как установлено в [4], обусловлено искажением (изменением) фронта световой волны при переходе наблюдателя из одной инерциальной системе отсчета в другую (явление).
5. Сечение светового луча, как было установлено в [4], и скорость света остаются неизменными (инвариантными) во всех инерциальных системах.
6. Реальная (истинная) скорость частиц или тел может превышать скорость света в вакууме.
Классики материализма были правы, утверждая, что пространство и время не простые атрибуты материи, а “коренные формы бытия материи”. Пространство и время это не тесто, которое мы можем безнаказанно ”искривлять” или ”квантовать”.
Может ли Специальная теория относительности рассматриваться как альтернативная теория по отношению к новой интерпретации? Нет, не может. Специальная теория относительности содержит гносеологические ошибки, которые приводят к внутренним логическим противоречиям этой теории. Последние стыдливо называются "парадоксами". Теория, имеющая гносеологические ошибки, не может считаться научной. Это в полной мере относится к Специальной теории относительности.
К сожалению, здесь мы не имеем возможности привести классификацию физических законов, которая дана в [5], вытекающую из взаимосвязи понятий "явление" и "сущность".
Литература.
1. В.Г. Левич. Курс теоретической физики. Т.1. - М.: Физматгиз, 1962.
2. Л. Бриллюен. Новый взгляд на теорию относительности. - М.: Мир, 1973.
3. В.А. Угаров. Специальная теория относительности. - М.: Наука, 1969.
4. В.А. Кулигин, Г.А. Кулигина, М.В. Корнева. Преобразование Лоренца и теория познания. / Воронеж. ун-т. - Воронеж, 1989. Деп. в ВИНИТИ 24.01.89, № 546.
5. V.A.Kuligin, G.A.Kuligina, M.V.Korneva. Epistemology and Special Relativity. Apeiron, (20:21). 1994.
6. М.В. Мостепаненко. Материалистическая сущность теории относительности Эйнштейна. - М.: Соц. - экон. лит.,1962.
7. Л.Д. Ландау. Е.М. Лифшиц. Теория поля. - М.: Физматгиз, 1961.
КРИЗИС РЕЛЯТИВИСТСКИХ ТЕОРИЙ
Часть 2. Анализ основ электродинамики.
Кулигин В.А., Кулигина Г.А., Корнева М.В.
Физический факультет, Воронежский госуниверситет
Университетская пл. 1, Воронеж, 394693, РОССИЯ
E-mail: kuligin@ el.main.vsu.ru
Установлено, что задача Коши для волнового уравнения не имеет единственного решения. Показано, что квазистатические явления электродинамики не имеют правильного объяснения в рамка кулоновской калибровки и калибровки Лоренца. Преобразование Лоренца имеет ограниченные пределы применимости.
Kuligin V.A., Kuligina G.A., Korneva M.V. It It is shown that a wave equation under initial conditions has no an unique solution. It is shown that quasistatical phenomena cannot be explained in framework of Lorentz's gauge or Coulomb's gauge. Lorentz's transformation is of limited usefulness.
Введение.
В предыдущей Части 1 мы искали сущность преобразования Лоренца, полагая, что это преобразование отвечает физическим явлениям. Например, существует точка зрения, согласно которой преобразование Лоренца имеет непосредственную поддержку со стороны электродинамики. Оказывается, что эта точка зрения ошибочна. Ниже будет показано, что преобразование Лоренца не применимо к явлениям электродинамики. Причина в математических ошибках.
Более того, исследуя трудности современных физических теорий, мы пришли к заключению, что часть этих трудностей имеет математические корни. Причина в том, что задача Коши для волновых уравнений, как это будет показано ниже, не имеет единственного решения. Это тем более удивительно, что существует теорема о существовании и единственности решения этой задачи [1]. Покажем это на примере.
1. Проблема единственности решения.
Пример нарушения единственности решения.
Рассмотрим для иллюстрации простой пример. Пусть некоторая функция U удовлетворяет однородному волновому уравнению с нулевыми начальными условиями.
![]() ;
; ![]() (1.1)
(1.1)
Первое решение. Мы имеем тривиальное решение [1], функция U равна нулю: U1=0. (1.2)
Второе решение. Запишем второе решение этой задачи.
 (1.3)
(1.3)
где: ![]() (1.4)
(1.4)
a,b,A суть некоторые постоянные величины (a >0, b>0).
Второе решение U2 (x,t) удовлетворяет поставленной задаче Коши, что можно подтвердить прямой проверкой. Это решение отлично от нуля и не имеет сингулярностей.
Таким образом, мы имеем два решения одной и той же задачи, т.е. теорема единственности решения не выполняется. Этот пример не уникален, и мы могли бы привести для иллюстрации другие примеры, например, для векторного уравнения в трехмерном пространстве с граничными условиями.
Метод получения второго решения.
Теперь мы рассмотрим метод получения второго решения для задачи Коши. Для наглядности мы рассмотрим построение решения неоднородного уравнения без граничных условий. Этот метод можно использовать и для задач с граничными условиями.
Пусть некоторая функция U является решением волнового уравнения
![]() (1.6)
(1.6)
где: U - некоторое скалярное поле; v - характеристическая скорость распространения; f - источник скалярного поля U.
Скалярное поле U должно удовлетворять следующим начальным условиям.
![]() (1.7)
(1.7)
Решение этой задачи существует [1]
и мы запишем его как ![]() . Мы будем называть это стандартное
решение прямым решением волнового уравнения или волновым решением.
. Мы будем называть это стандартное
решение прямым решением волнового уравнения или волновым решением.
Теперь нам предстоит построить второе решение. Мы будем искать это решение как сумму двух функций:
![]() (1.8)
(1.8)
После подстановки выражения (1.8) в уравнение (1.6) получаем:
![]() (1.9)
(1.9)
Поскольку решение (1.9) содержит уже две неизвестных функции вместо одной, мы должны добавить некоторое дополнительное условие. Существует много вариантов задания этого условия, например:
![]() (1.10)
(1.10)
где: F(r;t) любая интегрируемая функция; определяемая условиями конкретной физической задачи; a - некоторая константа.
В частности, в предыдущем примере мы выбрали второй вариант из (1.10), где f(r;t)=0 , а F(r;t) определяется выражением (1.4).
Положим для определенности, что функция V удовлетворяет уравнению Пуассона. Пусть
![]() (1.11)
(1.11)
Согласно [1], решение этого уравнения существует. Мы будем считать, что оно нам известно. Здесь же заметим, что принцип причинности не нарушается (см. [2] или Часть 3).
Рассмотрим теперь уравнение для потенциала u, которое следует из (1.6) и (1.11). Правая часть этого уравнения нам известна, поскольку, как мы условились, нам известно решение уравнения (1.11).
![]() (1.12)
(1.12)
Чтобы новое решение U2 удовлетворяло начальным условиям (1.7), мы должны задать другие начальные условия для u.
![]() (1.13)
(1.13)
Поскольку решение (1.11) нам известно,
начальные условия (1.13) также определены и известны. В общем случае решение
уравнения (1.12) при условии (1.13) существует [1]. Обозначим это решение как ![]() .
.
Таким образом, мы построили новое решение уравнения (1.6), удовлетворяющее заданным начальным условиям:
![]() (1.14)
(1.14)
Мы могли бы найти совершенно другое решение той же задачи. Для этой цели мы могли бы воспользоваться другими условиями из (1.10). Заметим, что рассмотренный нами метод получения второго решения может быть использован, например, как для уравнений Максвелла, так и для уравнения Шредингера.
Математические калибровки.
Для удобства мы назвали решение U1 уравнения (1.6) прямым решением волнового уравнения или волновым решением. Это волновое решение не содержит слагаемых, обладающих другими свойствами, например, мгновеннодействующих функций. Процедура поиска других решений, которые мы будем именовать как параллельные решения волнового уравнения, непосредственно связана с введением в новое решение дополнительной функции, которая обладает иными, отличными от волновых, пространственными и временными свойствами. Эту процедуру мы будем называть математической калибровкой волнового уравнения. Она имеет следующие особенности:
1. Каждая математическая калибровка имеет единственное решение, если мы не проводим над ней дальнейших процедур калибровочного характера.
2. Решения, соответствующие различным математическим калибровкам исходного волнового уравнения, отличаются друг от друга, т.е. не являются, вообще говоря, взаимозависимыми. Калибровочная инвариантность решений, т.е. независимость решения от выбора калибровки, в общем случае не имеет места.
Это очень важный и принципиальный результат, который требует переоценки многих положений физических теорий, опирающихся на мнение о калибровочной инвариантности. Это мнение уже превратилось в предрассудок или догму.
2. Калибровки в электродинамике.
Математические калибровки уравнений Максвелла.
Нарушение единственности решения обуславливает появление ряда новых проблем, например, проблему ковариантности физических уравнений и их решений. Это самостоятельная проблема, которую мы не будем здесь рассматривать. Чтобы сравнить особенности различных калибровок, мы будем считать, что уравнения и калибровки этих уравнений справедливы в некоторой фиксированной системе отсчета, где покоится наблюдатель. Иными словами, мы будем сравнивать решения, соответствующие различным калибровкам, в одной и той же фиксированной инерциальной системе отсчета.
Запишем уравнения Максвелла.
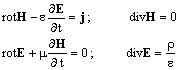 (2.1)
(2.1)
В системе (2.1) вектора E и H связаны между собой. Мы можем разделить уравнения для E и H.
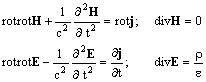 (2.2)
(2.2)
Прямое решение каждого из уравнений системы (2.2) Ew1 и Hw1 является волновым. Индекс "w" (wave - волновой) будет означать в дальнейшем, что мы имеем дело с волновым решением, т.е. с прямым решением любого волнового уравнения без использования каких-либо калибровок.
Запишем уравнения (2.1) в другой
калибровке. Для этой цели мы представим вектор Е в (2.1) как сумму:![]() (2.3)
(2.3)
где Eins является решением уравнения Пуассона.
Индекс "ins" (instantaneous - мгновеннодействующий) означает, что мы имеем дело с прямым решением уравнения Пуассона, например, т.е. с мгновеннодействующими полями и потенциалами.
Добавим для определенности следующие условия: ![]() (2.4)
(2.4)
Теперь система уравнений полностью определена и, используя процедуру разделения уравнений для Е и Н, мы можем записать следующую систему уравнений.
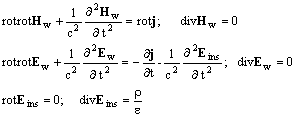 (2.5)
(2.5)
Система (2.5) описывает напряженность электрического поля E2=Eins2+ Ew2 и магнитного Hw2. Это есть параллельное решение по отношению к прямому решению Ew1 и Hw1 волновых уравнений (2.2). Поля, описываемые уравнениями (2.2), отличаются от полей, описываемых уравнениями (2.5).
Физические калибровки уравнений Максвелла.
Здесь легко просматривается параллель между уравнениями (2.2), (2.5) с одной стороны и известными калибровками уравнений Максвелла (2.1).
Если мы выразим в уравнении (2.5)
напряженность электрического поля Eins через градиент скалярного
потенциала -gradfins , Ew через векторный
потенциал ![]() и
напряженность магнитного поля Hw запишем как rotAw
, то получим кулоновскую калибровку уравнений Максвелла.
и
напряженность магнитного поля Hw запишем как rotAw
, то получим кулоновскую калибровку уравнений Максвелла.
![]() (2.6)
(2.6)
Если же мы положим Ew
= -gradfw![]() и H w =
rotAw в уравнениях (2.2), тогда мы придем к калибровке
Лоренца.
и H w =
rotAw в уравнениях (2.2), тогда мы придем к калибровке
Лоренца.
![]()
![]() ;
;
![]() ;
;![]() (2.7)
(2.7)
Следует заметить, что при таком выводе калибровок неизбежно появляются дополнительные поля (потенциалы) благодаря более высокому порядку операторов, действующих на E и H в уравнениях (2.2) и (2.5), по отношению к операторам в уравнениях (2.1). Эти поля не имеют своих источников и могут быть легко исключены из рассмотрения.
Из рассмотренной выше связи следует, что физическая калибровка электромагнитных потенциалов, связанная с выбором условия для divA, имеет прямую связь с математической калибровкой волновых уравнений и сводится к ней. Поэтому в дальнейшем мы будем говорить о калибровках вообще (без прилагательных: "физическая", "математическая" и т.д.). Теперь можно сравнить характеры решений уравнений (2.2) и (2.5). Решение уравнений (2.5) содержит мгновеннодействующую напряженность поля Eins, которая отсутствует в решении уравнений (2.2). В некоторых книгах [3], [4] утверждается, что Eins в кулоновской калибровке компенсируется некоторыми компонентами напряженности поля запаздывающего векторного потенциала и кулоновская калибровка полностью эквивалентна калибровке Лоренца. Это утверждение основывается на ошибочном предположении, что решение волнового уравнения единственно и не зависит от выбора калибровки. Независимость кулоновской калибровки от калибровки Лоренца рассмотрена в Приложении 1.
Необходимо сделать еще одно замечание. Проблема калибровки непосредственно связана с проблемой ковариантности уравнений. Это тем более важно, что мы установили отсутствие калибровочной инвариантности, т.е. зависимость решений одной и той же задачи от выбора калибровки. Как уже говорилось, проблема ковариантности - самостоятельная проблема и в этом докладе мы не будем ее рассматривать.
Калибровка калибровки Лоренца.
Теперь нам предстоит найти параллельное
решение калибровки Лоренца. Как известно, прямое решение в рамках этой
калибровки (2.7) имеет волновой характер и не содержит мгновеннодействующих
потенциалов и полей. ![]() (2.8)
(2.8)
Мы поступим стандартным способом. Представим потенциалы A и
f как сумму мгновеннодействующих и
волновых потенциалов. ![]() (2.9)
(2.9)
Пусть теперь потенциалы ![]() будут решениями
соответствующих уравнений Пуассона.
будут решениями
соответствующих уравнений Пуассона.
![]() (2.10)
(2.10)
Соответственно ![]() должны быть прямыми
решениями других волновых уравнений, удовлетворяющих соответствующим начальным
и граничным условиям.
должны быть прямыми
решениями других волновых уравнений, удовлетворяющих соответствующим начальным
и граничным условиям.
![]() ;
; ![]() ;
; ![]() (2.11)
(2.11)
Систему уравнений (2.10) и (2.11) можно условно назвать калибровкой калибровки Лоренца. Таким образом, параллельное решение имеет следующий вид:
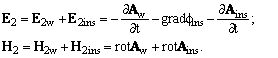 (2.12)
(2.12)
Нетрудно убедиться, что прямое решение (2.8) отличается от параллельного решения (2.12) того же уравнения. Здесь, например, мы имеем дело с двумя различными физическими механизмами излучения электромагнитных волн. Волновые поля (2.8) прямого решения генерируются непосредственно токами и зарядами, записанными в правой части уравнений. Волновые поля параллельного решения уравнений (2.11) возбуждаются мгновеннодействующими полями зарядов. Это следует из формы правой части уравнений (2.11). Помимо этого имеется еще одно принципиальное отличие. Электромагнитные поля в калибровке калибровки Лоренца можно разделить на два вида: мгновеннодействующие поля зарядов и электромагнитные волны. Поля зарядов всегда связаны с зарядами и определяются только величиной заряда. Если заряд покоится, его поле не зависит от предшествующей "истории" движения заряда. Напротив, электромагнитная волна, излучившись, "живет своей собственной жизнью". Она распространяется независимо от того, каково дальнейшее движение заряда. Электромагнитная волна и квазистатические поля зарядов, хотя и имеют взаимную связь, но обладают различными свойствами.
Напротив, стандартная калибровка Лоренца рассматривает квазистатические поля и электромагнитную волну как одинаковые поля с одинаковыми свойствами.
Предельный переход.
Формально математически мы можем записать следующие соотношения между решениями калибровки Лоренца (2.8) и калибровки калибровки Лоренца (2.12):
![]() . (2.13)
. (2.13)
Однако соотношения (2.13) не являются
корректными как с физической, так и с математической точек зрения. Они не
обусловлены причинно, поскольку поля ![]() не являются прямым решением
волнового уравнения (2.7), т.е. не удовлетворяют волновому уравнению. Поля
(2.7) принадлежат параллельному решению, т.е. другой калибровке.
не являются прямым решением
волнового уравнения (2.7), т.е. не удовлетворяют волновому уравнению. Поля
(2.7) принадлежат параллельному решению, т.е. другой калибровке.
Отсюда мы можем сделать следующий вывод. Предельный переход c®¥ следует использовать осторожно. В противном случае мы рискуем совершить незаконный переход из одной калибровки (например, калибровка Лоренца) в другую (калибровка калибровки Лоренца). Прямое решение (2.8) принципиально не может содержать мгновеннодействующих потенциалов.
Важное следствие.
Предельный переход от волнового уравнения и прямого решения к квазистатическому уравнению и параллельному решению при c®¥ не является законным! Квазистатические явления электродинамики должны описываться собственной системой уравнений.
3. Энергетические соотношения в калибровке Лоренца.
Тензор энергии-импульса.
Сразу же заметим, что, коль скоро решение зависит от выбора калибровки, каждая калибровка будет иметь свои законы сохранения. Причина в том, что поля, имеющие различную природу, будут создавать потоки энергии, которые имеют разные свойства. В этом смысле закон сохранения Пойнтинга не является универсальным, пригодным для любых калибровок.
Теперь мы выведем закон сохранения энергии для калибровки Лоренца. С этой целью запишем интеграл действия для электромагнитного поля [5].
![]() (3.1)
(3.1)
где: ![]() тензор
электромагнитного поля; dW - 4-мерный
объем (dx; dy; dz; icdt).
тензор
электромагнитного поля; dW - 4-мерный
объем (dx; dy; dz; icdt).
Для получения уравнений электромагнитного поля мы должны варьировать 4-потенциал Ak . Мы будем полагать, что 4-плотность тока jk не зависит от Ak.
![]()
(3.2)
После интегрирования по частям получим:
![]() (3.3)
(3.3)
где dSi - элемент 4-поверхности.
Во втором интеграле мы должны удовлетворить значениям для пределов интегрирования. Пределы интегрирования пространственных координат - бесконечность. Поля и потенциалы, как известно, на бесконечности равны нулю. Следовательно, на пространственных пределах интегрирования интеграл обращается в нуль. По условиям интегрирования начальная координата времени ta и конечная tb фиксированы и не варьируются. Поэтому в этих точках вариация интеграла dS равна нулю. Таким образом, второй интеграл равен нулю.
Вариация первого интеграла dS равна нулю, если интеграл имеет экстремум и интегрирование идет по экстремали. Поэтому в силу произвольности вариации 4-потенциала dAk , выражение в квадратных скобках внутри первого интеграла должно быть равно нулю. Это “уравнение движения” для электромагнитного поля или уравнение Эйлера для 4-потенциала.
![]() (3.4)
(3.4)
Перепишем это уравнение в классической форме.
![]()
![]() (3.5)
(3.5)
Условие Лоренца ¶Аi/¶xi=0 следует непосредственно из уравнения непрерывности для тока ¶ji/¶xi=0 и системы уравнений (3.5).
Второй интеграл (3.3), как мы убедились, не дает вклада в уравнения (3.4) и (3.5). Поэтому мы можем записать интеграл действия в более простой форме.
![]() (3.6)
(3.6)
где ![]() (3.7)
(3.7)
L это новая плотность функции Лагранжа для электромагнитного поля.
В этом нет ничего необычного, поскольку функция Лагранжа не определяется однозначным образом. Выражение (3.6) имеет вид:
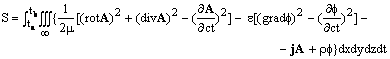 (3.8)
(3.8)
Опираясь на выражение (3.7) и используя метод получения тензора энергии-импульса электромагнитного поля [5], нетрудно записать выражение для этого тензора.
![]() (3.9)
(3.9)
Закон сохранения энергии для калибровки Лоренца.
Записанный тензор является симметричным. Из выражения (3.9) следует, что плотность энергии электромагнитного поля (компонент тензора T44) равна
![]() (3.10)
(3.10)
Энергия электромагнитного поля, заключенная в объеме V есть
![]() (3.11)
(3.11)
Рассмотрим теперь изменение энергии в этом объеме во времени.
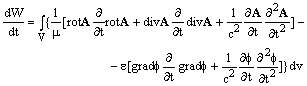 (3.12)
(3.12)
После интегрирования (3.12) по частям и использования выражений (3.5), мы получим:
![]()
![]() (3.13)
(3.13)
где no - единичная нормаль к поверхности S.
Потенциалы A и f являются независимыми, и мы можем записать два закона сохранения энергии для уравнений Максвелла в калибровке Лоренца в классической форме.
![]() (3.14)
(3.14)
где:
![]() - составляющие для скалярного
потенциала,
- составляющие для скалярного
потенциала,
![]() - составляющие для векторного
потенциала.
- составляющие для векторного
потенциала.
Заметим, что этот вывод читатель не обнаружат в стандартном многотомнике теоретической физики Ландау и Лифшица. В нем современная физика представлена только лакированным фасадом. Проблемы и трудности спрятаны в полном соответствии с традициями современного позитивизма. И, если о них упоминается, то вскользь как о неприятных, но непринципиальных моментах теории.
Три вектора плотности потока.
В соответствии с принципом суперпозиции векторный потенциал A и плотность тока j можно представить в виде суммы двух составляющих. Это соленоидальная (вихревая) и безвихревая составляющие плотности тока и векторного потенциала.
A = A1 + A2; j = j1 + j2 (3.15)
где: div A1 = 0; div j1 = 0; rot A2 = 0; rot j2 = 0.
Это не новая калибровка, а новое представление калибровки Лоренца.
Рассмотрим точечный источник потенциалов. Нетрудно видеть, что компоненты электрического и магнитного поля, обусловленные векторным потенциалом A1, всегда ортогональны компонентам электрического поля, обусловленного векторным потенциалом A2. Иными словами, имеют место следующие соотношения;
![]() (3.16)
(3.16)
На больших расстояниях от системы источников векторного потенциала, когда размеры области, в которой локализованы движущиеся заряды, весьма малы по сравнению с расстоянием от наблюдателя до этой области, соотношение (3.16) имеет место и для системы зарядов.
С учетом выражения (3.15) калибровка Лоренца принимает следующий вид:
![]() (3.17)
(3.17) ![]() (3.18)
(3.18)
![]() (3.19)
(3.19) ![]() (3.20)
(3.20)
Каждое уравнение имеет свою плотность потока и плотность энергии, которые представлены в Таблице 1.
Таблица 1. Энергетические компоненты волновых полей.
|
|
Поперечные волны векторного потенциала |
|
||
|
|
|
|
||
|
|
Продольные волны векторного потенциала |
|
||
|
|
|
|
||
|
|
Продольные волны скалярного потенциала |
|
||
|
|
|
|
||
Теперь мы можем сделать промежуточные выводы.
Во-первых, закон сохранения энергии Пойнтинга не является уникальным и универсальным. Это подтверждается нашей работой по решению проблемы электромагнитной массы [6] (см. также часть 5). В них показано, что в квазистатической электродинамике существуют другие энергетические соотношения. Например, имеет место закон Умова в его классической форме и закон баланса кинетической энергии, вербальная формулировка которого напоминает закон Ленца.
Во вторых, мы обращаем внимание на то, что энергия поля скалярного потенциала отрицательна. Как следствие, закон Кулона должен иметь другую формулировку: одноименные заряды должны притягиваться, а разноименные – отталкиваться (!). Эта проблема не нова. С ней постоянно
сталкиваются в квантовой электродинамике. В следующем параграфе мы проанализируем причину отрицательности энергии поля скалярного потенциала.
4. Продольные электромагнитные волны.
Убывание продольного поля на бесконечности.
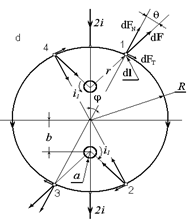
Рассмотрим систему зарядов, локализованных в области пространства, ограниченной некоторым радиусом а. В соответствии с теоремой Гаусса мы можем записать
![]() (4.1)
(4.1)
где: E - напряженность электрического поля; no - единичная нормаль к поверхности; qi - i-ый заряд системы внутри сферы радиуса а; V- объем, внутри которого расположена сфера радиуса а с зарядами.
Ясно, что поперечное электрическое поле векторного потенциала A1 не будет вносить свой вклад в продольную составляющую электрического поля в интеграле Гаусса. Поэтому при r®¥ мы можем рассматривать только продольные компоненты электрического поля, обусловленные потенциалами A2 и f.
![]() (4.2)
(4.2)
Сравнивая выражения (4.1) и (4.2), можно установить закон убывания продольного электрического поля.
![]() (4.3)
(4.3)
Из выражения (4.3)
следует: ![]() (4.4)
(4.4)
Таким образом, если сумма зарядов внутри сферы радиуса а не равна нулю, то поле убывает на бесконечности как r-2. Если же суммарный заряд равен нулю, и заряды образуют мультиполь высокого порядка, тогда продольное электрическое поле может убывать еще быстрее.
Компенсация продольных волн.
Теперь мы возвратимся к уравнениям (3.17) - (3.19) и Таблице 1. Поля, описываемые волновыми уравнениями, убывают, в общем случае, как
r-1. Например, поля, осциллирующие с частотой w, убывают как exp(-ikr)/r, где k - волновое число. Таким образом, мы сталкиваемся с противоречием. С одной стороны, продольное электрическое поле должно убывать не медленнее, чем r-2, с другой - продольное электрическое поле может убывать как r-1.
Естественно предположить, что плотности потоков S2 и S3 и плотности энергий w2 и w3 должны компенсировать друг друга при r ® ¥.
Запишем два интеграла:
![]() (4.5) ;
(4.5) ; ![]() (4.6)
(4.6)
где: P - общий поток электромагнитной энергии через поверхность сферы, окружающей источники; DW - плотность энергии в тонком сферическом слое Dr как показано на рис.1.
![]() (4.7)
(4.7)
![]() (4.8)
(4.8)
h - некоторое число, равное по модулю 1; знак h мы установим позже.
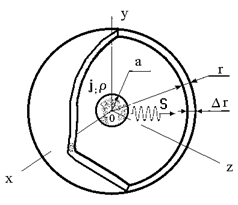
Рис. 1.
Представим векторный потенциал A в виде суммы (3.4) и предположим, что источники расположены внутри сферы радиуса а (r > > a). Рассмотрим потенциалы на поверхности сферы радиуса r . Здесь мы можем использовать условия ортогональности полей (3.5) , когда r ® ¥.
Интегралы (4.5) и (4.6) можно разделить на две независимых группы
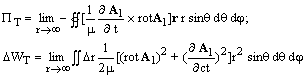 (4.9)
(4.9)
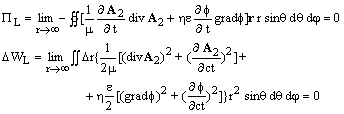 (4.10)
(4.10)
где: PT и PL - потоки, соответствующие поперечным и продольным волнам; DWT и DWL - энергии в тонком слое Dr соответственно для поперечных и продольных волн.
Поперечные волны уносят энергию в бесконечность и интегралы (4.9) не равны нулю.
Поток и энергия продольных волн (4.10) должны быть равны нулю благодаря компенсации. Оба выражения (4.10) удовлетворяются одновременно, если подынтегральные выражения равны нулю.
![]() (4.11)
(4.11)
![]() (4.12)
(4.12)
Мы видим, что выражение в квадратных скобках уравнения (4.12) всегда положительно. Следовательно, оно может равняться нулю только при h = - 1.
С учетом этого условия, два выражения (4.11) и (4.12) легко преобразуются к следующему виду.
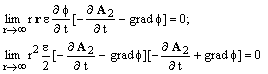 (4.13)
(4.13)
Из выражения (4.13) следует, что оба уравнения одновременно равны нулю, когда:
![]() (4.14)
(4.14)
где EL - напряженность продольного электрического поля (4.4).
Выражение (4.14) всегда справедливо в силу условия (4.4). Итак, продольные волны скалярного и векторного потенциалов, описываемые волновыми уравнениями, могут компенсировать друг друга при r®¥ тогда и только тогда, когда плотность потока и плотность энергии поля скалярного потенциала и соответствующие плотности продольного векторного потенциала имеют противоположные знаки.
Мы выяснили физическую причину отрицательного знака энергии и потока поля скалярного потенциала. При одинаковых знаках компенсация продольных волн невозможна.
5. Свойства калибровок.
Калибровка Лоренца.
Теперь мы можем обсудить особенности упомянутых выше калибровок. Мы видим, что калибровка Лоренца описывает продольные электрические волны скалярного и векторного потенциалов. Эти волны взаимно гасят друг друга на бесконечности и, в результате, их энергия не уносится в бесконечность. Однако вблизи источника излучения продольные электрические поля, определяемые запаздывающими потенциалами, существуют.
Мы выяснили также, что описание квазистатических явлений в рамках калибровки Лоренца невозможно, поскольку предельный переход при с®¥ не является математически законной операцией. Более того, даже если бы такой переход и существовал, описание квазистатических явлений натолкнулось бы на непреодолимые трудности. Энергия поля заряженной частицы будет отрицательной, и мы стаолкнемся с нарушением закона Кулона: одноименные заряды должны притягиваться, разноименные - отталкиваться, а энергия заряженного конденсатора будет иметь отрицательный знак (!). Конечно, можно попытаться исправить положение, изменив знак функции Лагранжа. Но при этом мы столкнулись бы с другой трудностью: энергия электромагнитных волн, излучаемая антенными системами, будет иметь отрицательный знак (!). Таким образом, калибровка Лоренца дает противоречивое описание явлений электродинамики.
Кулоновская калибровка.
Рассмотрим теперь кулоновскую калибровку. Благодаря тому, что правая часть уравнения для векторного потенциала содержит только соленоидальные источники, продольные волны запаздывающего потенциала отсутствуют даже вблизи источника излучения электромагнитных волн. Проблема компенсации продольных волн не возникает. Более того, энергия поля скалярного потенциала положительна и закон Кулона не нарушается. Тем не менее, кулоновская калибровка также имеет трудности. В рамках этой калибровки мы не можем описывать квазистатические магнитные явления.
Причина та же. Мы не имеем права использовать предельный переход с®¥ для волнового уравнения векторного потенциала А.
Таким образом, эти калибровки не могут быть использованы для описания квазистатических явлений в рамках классической электродинамики. Те же проблемы существуют и для уравнений Максвелла в их стандартной форме.
Заключение.
Итак, мы установили следующее.
1. Волновое уравнение не имеет единственного решения задачи Коши. Существуют прямое решение волнового уравнения и параллельные решения. Решение зависит от выбора калибровки волнового уравнения. Если выбранная калибровка зафиксирована, решение задачи Коши единственно.
2. Различные калибровки уравнений дают, в общем случае, различные решения задачи Коши. Калибровочная инвариантность, вообще говоря, не имеет места.
3. Предельный переход при c®¥ не всегда является законным.
4. Электромагнитные потенциалы играют важную роль в электродинамике. Поэтому поиск той единственной калибровки уравнений Максвелла, которая соответствовала бы результатам экспериментальных исследований физических явлений, крайне необходим. Возможно, это будет связано с пересмотром уравнений классической электродинамики.
5. Остается нерешенной проблема ковариантности уравнений электродинамики, т.е. поиск преобразования, которое связывало бы потенциалы и поля в различных системах отсчета.
Таковы формальные выводы. Остается удивительным тот факт, что уравнения Максвелла с успехом используются до сих пор. Можно предположить, что имеют место следующие причины. Во-первых, те расхождения между теорией и экспериментом, с которыми встречаются исследователи, либо не публикуются (отклоняются редакционными коллегиями), либо истолковываются как ошибки эксперимента самими исследователями. Во вторых, задачи, связанные с излучением электромагнитных волн, как правило, очень редко пересекаются с задачами описания квазистатических явлений электродинамики. Однако, там, где они пересекаются, возникают проблемы и трудности (электромагнитная масса заряда, реакция излучения ускоренного заряда и другие).
Выход мы видим в раздельном описании волновых полей и полей зарядов, поскольку свойства квазистатических полей зарядов и волновых полей различны. Более того, мы предполагаем, что требование ковариантности любых полей относительно преобразования Лоренца - слишком жесткое требование. Преобразование Лоренца не универсально и каждое из упомянутых полей, обладая своими специфическими свойствами, может удовлетворять каким-то своим преобразованиям.
Более жесткое заключение - следующее. Преобразование Лоренца потеряло поддержку со стороны электродинамики. Оно должно уступить свое место преобразованию Галилея. Наша мысль подкрепляется значительным количеством книг и статей, посвященных критике Специальной теории относительности с позиции теории и эксперимента (см., например, [7], [8], [9] и т.д.).
Приложение 1.
До настоящего времени считалось, что задача Коши для волнового уравнения имеет единственное решение. В силу этого делался закономерный вывод о независимости решения от выбора калибровки. Иными словами, решения в рамках калибровки Лоренца и в рамках кулоновской калибровки считались эквивалентными.
Теперь мы должны показать, что такой вывод не законен. Рассмотрим уравнения Максвелла в кулоновской калибровке (2.6).
![]() (А.1)
(А.1)
Решение этих уравнений должно содержать поле мгновеннодействующего потенциала fins , т.е. поле E=- gradfins.
В [3] и [4] утверждается, что
часть поля векторного потенциала ![]() компенсирует эту мгновеннодействующую
составляющую напряженности поля - gradfins
во всем свободном пространстве. Чтобы показать ошибочность этого заключения,
преобразуем правую часть векторного уравнения, используя уравнение непрерывности
для скалярного потенциала
компенсирует эту мгновеннодействующую
составляющую напряженности поля - gradfins
во всем свободном пространстве. Чтобы показать ошибочность этого заключения,
преобразуем правую часть векторного уравнения, используя уравнение непрерывности
для скалярного потенциала
![]() (А.2)
(А.2)
Будем для простоты считать, что скорость заряда v постоянна.
В результате правая часть векторного уравнения из (А.1) примет вид:
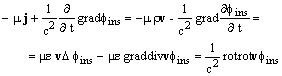 (А.3)
(А.3)
Компенсация поля - gradfins полем ![]() невозможна по следующим
причинам. Во-первых, правая часть уравнения для векторного потенциала
пропорциональна v/c. Следовательно, при v/c равном или близком к нулю мы не
можем иметь полную компенсацию. Во вторых, источник поля векторного потенциала
(правая часть уравнения (А.3)) имеет соленоидальный характер. Он может
создавать только соленоидальный векторный потенциал А. Попытка создать в
свободном пространстве поле полярного вектора, используя только
источники соленоидальных полей, бессмысленна.
невозможна по следующим
причинам. Во-первых, правая часть уравнения для векторного потенциала
пропорциональна v/c. Следовательно, при v/c равном или близком к нулю мы не
можем иметь полную компенсацию. Во вторых, источник поля векторного потенциала
(правая часть уравнения (А.3)) имеет соленоидальный характер. Он может
создавать только соленоидальный векторный потенциал А. Попытка создать в
свободном пространстве поле полярного вектора, используя только
источники соленоидальных полей, бессмысленна.
Иногда говорят, что компенсация мгновеннодействующего поля следует непосредственно из градиентной инвариантности, связывающей кулоновскую калибровку с калибровкой Лоренца. Рассмотрим и этот подход.
Как известно, напряженности электрического E и магнитного поля H сохраняют свои значения при следующем преобразовании
![]() (А.4)
(А.4)
где: А и f исходные электромагнитные потенциалы; A'
и f' новые электромагнитные
потенциалы; f есть некоторая функция (калибровочный потенциал),
удовлетворяющая однородному волновому уравнению: ![]() (А.5)
(А.5)
Очевидно, что калибровочный потенциал f не является мгновеннодействующим.
Запишем уравнения Максвелла в калибровке Лоренца.
![]() ;
; ![]() ;
; ![]()
(А.6)
Чтобы получить из этих уравнений
уравнения Максвелла в кулоновской калибровке, вводят условие ![]() . Используя это
условие и выражение (А.4), подставим A и f
, выраженные через A' и f'.
. Используя это
условие и выражение (А.4), подставим A и f
, выраженные через A' и f'.
В результате мы получим:
![]() (А.7)
(А.7)
Казалось бы, что теперь мы действительно имеем дело с кулоновской калибровкой. В действительности мы должны помнить, что потенциал f и, следовательно, потенциалы f'w и fw должны быть решениями однородного волнового уравнения (см. (А.5)).
![]() (А.8)
(А.8)
Это противоречит уравнению Пуассона для скалярного потенциала (А.7):
![]() (А.9)
(А.9)
Уравнения (А.8) и (А.9) несовместны. Следовательно, кулоновская калибровка не является следствием калибровки Лоренца. Градиентная инвариантность не имеет места. Этот вывод имеет принципиальное значение и для квантовой электродинамики.
Литература.
1. А.Н. Тихонов. А.А. Самарский. Уравнения математической физики. - М; ГИФМЛ, 1954.
2. В А. Кулигин. Причинность и взаимодействие в физике // Детерминизм в современной науке. Воронеж, 1987.
3. В.Л. Гинзбург. Теоретическая физика и астрофизика. -М; ГИФМЛ, 1987.
4. Д. Джексон. Классическая электродинамика. –М; Мир. 1965.
5. Л.Д. Ландау, Е.М. Лифшиц. Теория поля. - М; Физматгиз, 1961.
6. V.A.Kuligin, G.A.Kuligina, M.V.Korneva.. The electromagnetic mass of a charged particle. Apeiron, vol.3, №1, 1996.
7. V.A.Kuligin, G.A.Kuligina, M.V.Korneva. Epistemology and Special Relativity. Apeiron, (20:21). 1994
8. B.G. Wallace. Radar testing of the relative velocity of light in space. Spectroscope Letters, vol.2, №12, 1969.
9. H.C. Hayden. Stellar aberration. Galilean Electrodynamics, vol. 4, № 5, 1993.
КРИЗИС РЕЛЯТИВИСТСКИХ ТЕОРИЙ
Часть 3. Причинность в физике.
Кулигин В.А., Кулигина Г.А., Корнева М.В.
Физический факультет, Воронежский госуниверситет
Университетская пл. 1, Воронеж, 394693, РОССИЯ
E-mail: kuligin@ el.main.vsu.ru
Показано, что существуют две модели причинности. Эти модели имеют взаимную связь. Показано, что мгновенные взаимодействия не противоречат принципу причинности. Показано, что скорость распространения взаимодействий является бессодержательным понятием.
Kuligin V.A., Kuligina G.A., Korneva M.V. It is shown that two causality models exist. These modelels have interplay between one another. It is shown that instantaneous interactions are not in conflict with causality. It is shown that the interaction velocity is hollow concept.
Введение.
Мы должны раскрыть ошибочность постулата А.Эйнштейна о существовании предельной скорости распространения взаимодействий. Сейчас этот постулат рассматривается как обобщение причинности в физике.
Вопрос о причинности - сложный вопрос. Суть в том, что причинно-следственные отношения содержат много нерешенных проблем. Без их решения все наши рассуждения будут иметь частный характер, без достаточной доказательной силы. Именно данное обстоятельство заставляет нас рассмотреть сначала общие проблемы причинности.
Философская категория "причинность", как и принцип причинности, связанный с ней, восходит к основополагающему принципу диалектического материализма о всеобщей связи и взаимной обусловленности явлений материального мира. Содержание категории "причинность" может быть раскрыто через содержание и конкретизацию взаимной связи исходных философских категорий "причина" и "следствие" (причинно-следственное отношение).
Как известно, раскрытие содержания и конкретизация понятий должны опираться на ту или иную конкретную модель взаимной связи понятий. Модель, объективно отражая определенную сторону связи, имеет границы применимости, за пределами которых ее использование ведет к ложным выводам, но в границах своей применимости она должна обладать не только образностью, наглядностью и конкретностью, но и иметь эвристическую ценность.
Многообразие проявлений причинно-следственных связей в материальном мире обусловило существование нескольких моделей причинно-следственных отношений. Исторически сложилось так, что любая модель этих отношений может быть сведена к одному из двух основных типов моделей или их сочетанию.
а) Модели, опирающиеся на временной подход (эволюционные модели). Здесь главное внимание акцентируется на временной стороне причинно-следственных отношений. Одно событие — "причина" — порождает другое событие — "следствие", которое во времени отстает от причины (запаздывает). Запаздывание — отличительный признак эволюционного подхода. Причина и следствие взаимно обусловлены. Однако ссылка на порождение следствия причиной (генезис), хотя и законна, но привносится в определение причинно-следственной связи как бы со стороны, извне. Она фиксирует внешнюю сторону этой связи, не захватывая глубоко сущности.
Эволюционный подход развивался Ф. Бэконом, Дж. Миллем и др. Крайней полярной точкой эволюционного подхода явилась позиция Юма. Юм игнорировал генезис, отрицая объективный характер причинности, и сводил причинную связь к простой регулярности событий.
б) Модели, опирающиеся на понятие "взаимодействие" (диалектические[2] модели). Главное внимание здесь уделяется взаимодействию как источнику причинно-следственных отношений. В роли причины выступает само взаимодействие. Большое внимание этому подходу уделял Кант, но наиболее четкую форму диалектический подход к причинности приобрел в работах Гегеля. Из современных советских философов этот подход развивал Г. А. Свечников [1], который стремился дать материалистическую трактовку одной из диалектических моделей причинно-следственной связи.
Существующие и использующиеся в настоящее время модели различным образом вскрывают механизм причинно-следственных отношений, что приводит к разногласиям и создает основу для философских дискуссий. Острота обсуждения и полярный характер точек зрения свидетельствуют об их актуальности [2].
Выделим некоторые из дискутируемых проблем.
а) Проблема одновременности причины и следствия. Это основная проблема. Одновременны ли причина и следствие или разделены интервалом времени? Если причина и следствие одновременны, то почему причина порождает следствие, а не наоборот? Если же причина и следствие неодновременны, может ли существовать "чистая" причина, т. е. причина без следствия, которое еще не наступило, и неизвестно: наступит ли, и "чистое" следствие, когда действие причины кончилось, а следствие еще продолжается? Что происходит в интервале между причиной и следствием, если они разделены во времени, и т. д.?
б) Проблема однозначности причинно-следственных отношений. Порождает ли одна и та же причина одно и то же следствие или же одна причина может порождать любое следствие из нескольких потенциально возможных? Может ли одно и то же следствие быть порожденным любой из нескольких возможных причин?
в) Проблема обратного воздействия следствия на свою причину.
г) Проблема связи причины, повода и условий. Могут ли при определенных обстоятельствах причина и условие меняться ролями: причина стать условием, а условие — причиной? Какова объективная взаимосвязь и отличительные признаки причины, повода и условия?
Решение этих проблем зависит от выбранной модели, т. е. в значительной степени от того, какое содержание будет заложено в исходные категории "причина" и "следствие". Дефиниционный характер многих трудностей проявляется, например, уже в том, что нет единого ответа на вопрос, что следует понимать под "причиной". Одни исследователи под причиной мыслят материальный объект, другие [3]—явление, третьи [4]— изменение состояния, четвертые — взаимодействие и т. д.
К решению проблемы не ведут попытки выйти за рамки модельного представления и дать общее, универсальное определение причинно-следственной связи. В качестве примера можно привести следующее определение[5]:
"Причинность — это такая генетическая связь явлений, в которой одно явление, называемое причиной, при наличии определенных условий неизбежно порождает, вызывает, приводит к жизни другое явление, называемое следствием".
Это определение формально справедливо для большинства моделей, но, не опираясь на модель, оно не может разрешить поставленных проблем (например, проблему одновременности) и потому имеет ограниченную теоретико-познавательную ценность.
Решая упомянутые выше проблемы, большинство авторов стремятся исходить из современной физической картины мира и, как правило, не уделяют внимания гносеологии. Между тем, на наш взгляд, здесь существуют две проблемы, имеющие важное значение: проблема удаления элементов антропоморфизма из понятия причинности и проблема непричинных связей в естествознании. Суть первой проблемы в том, что причинность как объективная философская категория должна иметь объективный характер, не зависящий от познающего субъекта и его активности. Суть второй проблемы: признавать ли причинные связи в естествознании всеобщими и универсальными или считать, что такие связи имеют ограниченный характер и существуют связи непричинного типа, отрицающие причинность и ограничивающие пределы применимости принципа причинности? Мы считаем, что принцип причинности имеет всеобщий и объективный характер и его применение не знает ограничений.
Итак, два типа моделей, объективно отражая некоторые важные стороны и черты причинно-следственных связей, находятся в известной степени в противоречии, поскольку различным образом решают проблемы одновременности, однозначности и др., но вместе с тем, объективно отражая некоторые стороны причинно-следственных отношений, они должны находиться во взаимной связи. Наша задача — выявить эту связь и уточнить модели.
1. Границы эволюционной модели.
Попытаемся установить границу применимости моделей эволюционного типа. Причинно-следственные цепи, удовлетворяющие эволюционным моделям, как правило, обладают свойством транзитивности [6]. Если событие А есть причина события В (В—следствие А), если, в свою очередь, событие В есть причина события С, то событие А есть причина события С.
Если А→В и В→С, то А→ С.
Таким способом составляются простейшие причинно-следственные цепи. Событие В может выступать в одном случае причиной, в другом - следствием.
Свойство транзитивности позволяет также провести детальный анализ причинной цепи. Он состоит в расчленении конечной цепи на более простые причинно-следственные звенья.
Если А→С , то А→В1, В1→В2,..., ВN→C.
Но обладает ли конечная причинно-следственная цепь свойством бесконечной делимости? Может ли число звеньев конечной цепи N стремиться к бесконечности?
Опираясь на закон перехода количественных изменений в качественные, можно утверждать, что при расчленении конечной причинно-следственной цепи мы столкнемся с таким содержанием отдельных звеньев цепи, когда дальнейшее деление станет бессмысленным. Заметим, что бесконечную делимость, отрицающую закон перехода количественных изменений в качественные, Гегель именовал "дурной бесконечностью"[3].
Материализм утверждает, что в основе причинно-следственных связей лежит не самопроизвольное волеизъявление, не прихоть случая и не божественный перст, а универсальное взаимодействие. В природе нет самопроизвольного возникновения и уничтожения движения, есть взаимные переходы одних форм движения материи в другие, от одних материальных объектов к другим, и эти переходы не могут происходить иначе, чем через посредство взаимодействия материальных объектов. Такие переходы, обусловленные взаимодействием, порождают новые явления, изменяя состояние взаимодействующих объектов.
Взаимодействие универсально и составляет основу причинности. Как справедливо отмечал Гегель, "взаимодействие есть причинное отношение, положенное в его полном развитии" [7]. Еще более четко сформулировал эту мысль Ф. Энгельс в "Диалектике Природы":
"Взаимодействие — вот первое, что выступает перед нами, когда мы рассматриваем движущуюся материю в целом с точки, зрения теперешнего естествознания ... Так естествознанием подтверждается то ... что взаимодействие является истинной causa finalis вещей. Мы не можем пойти дальше познания этого взаимодействия именно потому, что позади его нечего больше познавать".
2. Диалектическая модель причинности.
Поскольку взаимодействие составляет основу причинности, рассмотрим взаимодействие двух материальных объектов, схема которого приведена на рис.1. Данный пример не нарушает общности рассуждений, поскольку взаимодействие нескольких объектов сводится к парным взаимодействиям и может быть рассмотрено аналогичным способом.
Нетрудно видеть, что при взаимодействии оба объекта одновременно воздействуют друг на друга (взаимность действия). При этом происходит изменение состояния каждого из взаимодействующих объектов. Нет взаимодействия - нет изменения состояния [8]. Поэтому изменение состояния какого-либо одного из взаимодействующих объектов можно рассматривать как частное следствие причины — взаимодействия. Изменение состояний всех объектов в их совокупности составит полное следствие.
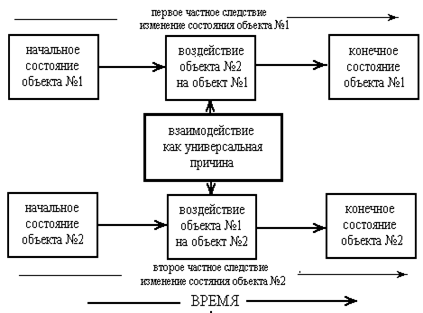
Pис. 1. Диалектическая (диалектическая) модель причинности
Очевидно, что такая причинно-следственная модель элементарного звена эволюционной модели принадлежит классу диалектических. Следует подчеркнуть, что данная модель не сводится к подходу, развивавшемуся Г. А. Свечниковым, поскольку под следствием Г. А. Свечников, по словам В. Г. Иванова [9], понимал "...изменение одного или всех взаимодействовавших объектов или изменение характера самого взаимодействия, вплоть до его распада или преобразования". Что касается изменения состояний, то это изменение Г. А. Свечников относил к непричинному виду связи.
Итак, мы установили, что эволюционные модели в качестве элементарного, первичного звена содержат диалектическую модель, опирающуюся на взаимодействие и изменение состояний. Несколько позже мы вернемся к анализу взаимной связи этих моделей и исследованию свойств эволюционной модели. Здесь нам хотелось бы отметить, что смена явлений в эволюционных моделях, отражающих объективную реальность, происходит не в силу простой регулярности событий (как у Д. Юма), а в силу обусловленности, порожденной взаимодействием (генезис). Поэтому хотя ссылки на порождение (генезис) и привносятся в определение причинно-следственных отношений в эволюционных моделях, но они отражают объективную природу этих отношений и имеют законное основание.
Вернемся к диалектической модели. По своей структуре и смыслу она превосходно согласуется с первым законом диалектики — законом единства и борьбы противоположностей, если интерпретировать:
— единство — как существование объектов в их взаимной связи (взаимодействии);
— противоположности — как взаимоисключающие тенденции и характеристики состояний, обусловленные взаимодействием;
— борьбу — как взаимодействие;
— развитие — как изменение состояния каждого из взаимодействующих материальных объектов.
Поэтому модель, опирающаяся на взаимодействие как причину, названа диалектической моделью причинности. Из аналогии диалектической модели и первого закона диалектики следует, что причинность выступает как отражение объективных диалектических противоречий в самой природе, в отличие от субъективных диалектических противоречий, возникающих в сознании человека. Диалектическая модель причинности есть отражение объективной диалектики природы.
Рассмотрим пример, иллюстрирующий применение диалектической модели причинно-следственных отношений. Таких примеров, которые объясняются с помощью данной модели, можно найти достаточно много в естественных науках (физике, химии и др.), поскольку понятие "взаимодействие" является основополагающим в естествознании.
Возьмем в качестве примера упругое столкновение двух шаров: движущегося шара А и неподвижного шара В. До столкновения состояние каждого из шаров определялось совокупностью признаков Сa и Сb (импульс, кинетическая энергия и т. д.). После столкновения (взаимодействия) состояния этих шаров изменились. Обозначим новые состояния С'a и С'b. Причиной изменения состояний (Са→ С'a и Сb→ С'b) явилось взаимодействие шаров (столкновение); следствием этого столкновения стало изменение состояния каждого шара.
Как уже говорилось, эволюционная модель в данном случае малопригодна, поскольку мы имеем дело не с причинной цепью, а с элементарным причинно-следственным звеном, структура которого не сводится к эволюционной модели. Чтобы показать это, проиллюстрируем данный пример объяснением с позиции эволюционной модели: "До столкновения шар А покоился, поэтому причиной его движения является шар В, который ударил по нему". Здесь шар В выступает причиной, а движение шара А — следствием. Но с тех же самых позиций можно дать и такое объяснение: "До столкновения шар В двигался равномерно по прямолинейной траектории. Если бы не шар А, то характер движения шара В не изменился бы". Здесь причиной уже выступает шар А, а следствием — состояние шара В.
Приведенный пример показывает:
а) определенную субъективность, которая возникает при применении эволюционной модели за пределами границ ее применимости: причиной может выступать либо шар А, либо шар В; такое положение связано с тем, что эволюционная модель выхватывает одну частную ветвь следствия и ограничивается ее интерпретацией;
б) типичную гносеологическую ошибку. В приведенных выше объяснениях с позиции эволюционной модели один из однотипных материальных объектов выступает в качестве "активного", а другой — в качестве "страдательного" начала. Получается так, будто один из шаров наделен (по сравнению с другим) "активностью", "волей", "желанием", подобно человеку. Следовательно, только благодаря этой "воле" мы и имеем причинное отношение. Подобная гносеологическая ошибка определяется не только из-за использования эволюционной модели причинности за пределами границ ее применимости, но и образностью, присущей живой человеческой речи, и типичным психологическим переносом свойств, характерных для сложной причинности на простое причинно-следственное звено. И такие ошибки весьма характерны при использовании эволюционной модели за пределами границ ее применимости. Они встречаются в некоторых определениях причинности. Например, [10]:
"Итак, причинность определяется как такое воздействие одного объекта на другой, при котором изменение первого объекта (причина) предшествует изменению другого объекта и необходимым, однозначным образом порождает изменение другого объекта (следствие)".
Трудно согласиться с таким определением, так как совершенно не ясно, почему при взаимодействии (взаимном действии!) объекты должны деформироваться не одновременно, а друг за другом? Какой из объектов должен деформироваться первым, а какой вторым (проблема приоритета: кто первый начал?)?
3. Свойства диалектической модели.
Рассмотрим теперь, какие качества удерживает в себе диалектическая модель причинности. Отметим среди них следующие: объективность, универсальность, непротиворечивость, однозначность.
Объективность причинности проявляется в том, что взаимодействие выступает как объективная причина, по отношению к которой взаимодействующие объекты являются равноправными. Здесь не остается возможности для антропоморфного или же просто субъективного истолкования. Универсальность обусловлена тем, что в основе причинности всегда лежит взаимодействие. Причинность универсальна, как универсально само взаимодействие. Непротиворечивость обусловлена тем, что, хотя причина и следствие (взаимодействие и изменение состояний) совпадают во времени, они отражают различные стороны причинно-следственных отношений. Взаимодействие предполагает пространственную связь объектов, изменение состояния — связь состояний каждого из взаимодействующих объектов во времени.
Помимо этого диалектическая модель устанавливает однозначную связь в причинно-следственных отношениях независимо от способа математического описания взаимодействия. Более того, диалектическая модель, будучи объективной и универсальной, не предписывает естествознанию ограничений на характер взаимодействий. В рамках данной модели справедливы и мгновенное дально- или близкодействие, и взаимодействие с любыми конечными скоростями. Появление подобного ограничения в определении причинно-следственных отношений явилось бы типичной метафизической догмой, раз и навсегда постулирующей характер взаимодействия любых систем, навязывая физике и другим наукам натурфилософские рамки со стороны философии, либо ограничило пределы применимости модели настолько, что польза от такой модели оказалась бы весьма скромной.
Здесь уместно было бы остановиться на вопросах, связанных с конечностью скорости распространения взаимодействий. Рассмотрим пример. Пусть имеются два неподвижных заряда. Если один из зарядов начал двигаться с ускорением, то электромагнитная волна подойдет ко второму заряду с запаздыванием (кулоновским взаимодействием мы пренебрегаем). Не противоречит ли данный пример диалектической модели и, в частности, свойству взаимности действия, поскольку при таком взаимодействии заряды оказываются в неравноправном положении? Нет, не противоречит. Данный пример описывает не простое взаимодействие, а сложную причинную цепь, в которой можно выделить три различных звена.
1. Взаимодействие первого заряда с объектом, который вызывает его ускорение. Результат этого взаимодействия - изменение состояния источника, воздействовавшего на заряд, и в частности потеря этим источником части энергии, изменение состояния первого заряда (ускорение) и появление электромагнитной волны, которая излучилась первым зарядом при его ускоренном движении.
2. Процесс распространения электромагнитной волны, излученной первым зарядом.
3. Процесс взаимодействия второго заряда с электромагнитной волной. Результат взаимодействия — ускорение второго заряда, рассеяние первичной электромагнитной волны и излучение электромагнитной волны вторым зарядом.
В данном примере мы имеем два различных взаимодействия, каждое из которых укладывается в диалектическую модель причинности. Таким образом, диалектическая модель превосходно согласуется как с классическими, так и с релятивистскими теориями, а конечная скорость распространения взаимодействий не является необходимой для диалектической модели причинности и для причинности вообще.
Из Специальной теории относительности известно, что скорость распространения взаимодействий не может превышать скорости света. Какое содержание заложено в понятие "скорость распространения взаимодействий"? По-видимому, нам прежде следует определить содержание понятия "взаимодействие".
"Взаимодействие" это философская категория. Ф.Энгельс определял "взаимодействие" как "движение материи" в широком смысле этих слов. Оно связано с перераспределением энергии между взаимодействующими объектами, с переходами одних видов энергии в другие, с изменением импульсов взаимодействующих тел и т.д.
Как мы видим, взаимодействие не есть субстанция или материальный объект. Это не спринтер, который мечется от одного тела к другому и обратно со скоростью света..
С точки зрения диалектического материализма взаимодействие есть основа или сущность явлений. Как сущность взаимодействие не должно зависеть от наблюдателя, от субъективного выбора им инерциальной системы отсчета. О какой скорости, не зависящей от выбора инерциальной системы отсчета, может идти речь? Именно по этой главной причине любая (даже не предельная!) скорость распространения взаимодействий есть "пустое", бессодержательное понятие, понятие без физического смысла (набор слов). Именно по этой причине апологеты не могут дать как строгое определение этого понятия, так и определить методику измерения скорости распространения взаимодействия в пространстве.
Касаясь диалектической модели причинности, отметим, что ей не противоречат реакции распада и синтеза объектов. В этом случае между объектами либо разрушается относительно устойчивая связь как особый вид взаимодействия, либо такая связь образуется в результате взаимодействия.
Поскольку квантовые теории (равно как и классические) широко используют категории "взаимодействие" и "состояние", диалектическая модель принципиально применима и в этой области естествознания. Встречающиеся иногда трудности обусловлены, на наш взгляд, тем, что, обладая хорошо развитым математическим формализмом, квантовые теории еще недостаточно полно развиты и отточены в плане понятийной интерпретации[4]. Это одно из свидетельств того, что квантовые теории находятся в стадии становления и развития и не достигли уровня внутренней завершенности, свойственной классическим теориям.
Но о проблемах становления квантовых теорий свидетельствует не только интерпретация y-функции. Хотя релятивистская механика и электродинамика на первый взгляд представляются законченными теориями, более глубокий анализ показывает, что по ряду причин эти теории также не избежали противоречий и внутренних трудностей. Например, в электродинамике существуют проблема электромагнитной массы, проблема реакции излучения заряда и др. Неудачи в попытках разрешения этих проблем в рамках самих теорий в прошлом и бурное развитие теорий микромира породили надежду, что развитие квантовых теорий поможет ликвидировать трудности. А до тех пор они должны восприниматься как неизбежное "зло", с которым, так или иначе, приходится мириться и ждать успехов от квантовых теорий.
В то же время квантовые теории сами столкнулись со многими проблемами и противоречиями. Любопытно заметить, что часть этих трудностей имеет "классическую" природу, т. е. досталась "по наследству" от классических теорий и обусловлена их внутренней незавершенностью. Получается "порочный круг": разрешение противоречий классических теорий мы возлагаем на квантовые теории, а трудности квантовых определяются противоречиями классических.
Со временем надежда на способность квантовых теорий устранить противоречия и трудности в теориях классических стала угасать, но до сих пор интерес к разрешению противоречий классических теорий в рамках их самих все еще остается на втором плане.
Таким образом, трудности, встречающиеся иногда при объяснении явлений микромира с позиции причинности, имеют объективное происхождение и объясняются особенностями становления квантовых теорий, но они не являются принципиальными, запрещающими или ограничивающими применение принципа причинности в микромире, в частности применение диалектической модели причинности.
Причинность и взаимодействие всегда взаимосвязаны. Если взаимодействие обладает свойствами всеобщности, универсальности и объективности, то столь же универсальны, всеобщи и объективны причинно-следственные связи и отношения. Поэтому в принципе нельзя согласиться с утверждениями Бома, что при описании явлений микромира можно в одних случаях опираться на философский индетерминизм, в других — придерживаться принципа причинности [12]. Мы считаем глубоко ошибочной мысль В. Я. Перминова о том, что "понятие дополнительности указывает путь примирения (курсив наш — авторы) детерминизма и индетерминизма" [13], независимо от того, относится эта мысль к философии естествознания или к конкретной естественнонаучной теории. Путь примирения материалистической точки зрения с позицией современного агностицизма в данном вопросе есть эклектика, есть отрицание объективной диалектики. Путь становления квантовых теорий лежит не через отрицание или ограничение, а через утверждение причинности в микромире.
4. Особенности эволюционной модели.
Если в начале нашей работы мы шли от эволюционной модели причинности к диалектической, то теперь предстоит обратный путь от диалектической модели к эволюционной. Это необходимо, чтобы правильно оценить взаимную связь и отличительные особенности эволюционной модели.
Уже в неразветвленной линейной причинно-следственной цепи мы вынуждены отказаться от полного описания всех причинно-следственных отношений, т. е. не учитываем некоторые частные следствия. Диалектическая модель позволяет неразветвленные линейные причинно-следственные цепи свести к двум основным типам.
а) Объектная причинная цепь. Образуется тогда, когда мы выделяем какой-либо материальный объект и следим за изменением его состояния во времени. Примером могут служить наблюдения за состоянием броуновской частицы, или за эволюциями космического корабля, или за распространением электромагнитной волны от антенны передатчика до антенны приемника.
б) Информационная причинная цепь. Появляется, когда мы следим не за состоянием материального объекта, а за некоторым информирующим явлением, которое в процессе взаимодействий различных материальных объектов связано последовательно во времени с различными объектами. Примером может служить передача устной информации с помощью эстафеты и т. п.
Все линейные неразветвленные причинные цепи сводятся к одному из этих двух типов или к их комбинации. Такие цепи описывают с помощью эволюционной модели причинности. При эволюционном описании взаимодействие остается на втором плане, а на первый план выходит материальный объект или индикатор его состояния. В силу этого главное внимание сосредоточивается на описании последовательности событий во времени. Поэтому данная модель получила название эволюционной.
Линейная неразветвленная причинная цепь сравнительно легко поддается анализу с помощью сведения ее к совокупности элементарных звеньев и анализа их посредством диалектической модели. Но такой анализ не всегда возможен.
Существуют сложные причинные сети, в которых простые причинно-следственные цепочки пересекаются, ветвятся и вновь пересекаются. Это приводит к тому, что применение диалектической модели делает анализ громоздким, а иногда и технически невозможным.
Помимо этого нас часто интересует не сам внутренний процесс и описание внутренних причинно-следственных отношений, а начальное воздействие и его конечный результат. Подобное положение часто встречается при анализе поведения сложных систем (биологических, кибернетических и др.). В таких случаях детализация внутренних процессов во всей их совокупности оказывается избыточной, ненужной для практических целей, загромождающей анализ. Все это обусловило ряд особенностей при описании причинно-следственных отношений с помощью эволюционных моделей. Перечислим эти особенности.
1. При эволюционном описании причинно-следственной сети полная причинная сеть огрубляется. Выделяются главные цепи, а несущественные отсекаются, игнорируются. Это значительно упрощает описание, но подобное упрощение достигается ценой потери части информации, ценой утраты однозначности описания.
2. Чтобы сохранить однозначность и приблизить описание к объективной реальности, отсеченные ветви и причинные цепи заменяются совокупностью условий. От того, насколько правильно выделена основная причинная цепь и насколько полно учтены условия, компенсирующие огрубление, зависят полнота, однозначность и объективность причинно-следственного описания и анализа.
3. Выбор той или иной причинно-следственной цепи в качестве главной определяется во многом целевыми установками исследователя, т. е. тем, между какими явлениями он хочет проанализировать связь. Именно целевая установка заставляет выискивать главные причинно-следственные цепи, а отсеченные заменять условиями. Это приводит к тому, что при одних установках главную роль выполняют одни цепи, а другие заменяются условиями. При других установках эти цепи могут стать условиями, а роль главных будут играть те, что раньше были второстепенными. Таким образом, причины и условия меняются ролями.
Условия играют важную роль, связывая объективную причину и следствие. При различных условиях, влияющих на главную причинную цепь, следствия будут различными. Условия как бы создают то русло, по которому течет цепь исторических событий или развитие явлений во времени. Поэтому для выявления глубинных, сущностных причинно-следственных отношений необходим тщательный анализ, учет влияния всех внешних и внутренних факторов, всех условий, влияющих на развитие главной причинной цепи, и оценка степени влияния.
4. Эволюционное описание основное внимание уделяет не взаимодействию, а связи событий или явлений во времени. Поэтому содержание понятий "причина" и "следствие" изменяется, и это весьма важно учитывать. Если в диалектической модели взаимодействие выступает истинной causa finalis — конечной причиной, то в эволюционной — действующей причиной (causa activa) становится явление или событие.
Следствие также меняет свое содержание. Вместо связи состояний материального объекта при его взаимодействии с другим в качестве следствия выступает некоторое событие или явление, замыкающее причинно-следственную цепь. В силу этого причина в эволюционной модели всегда предшествует следствию.
5. В указанном выше смысле причина и следствие в эволюционной модели могут выступать как одно-качественные явления или события, с двух сторон замыкающие причинно-следственную цепь. Следствие одной цепи может явиться причиной и началом другой цепи, следующей за первой во времени. Это обстоятельство обусловливает свойство транзитивности эволюционных моделей причинности.
Мы здесь коснулись только главных особенностей и отличительных признаков эволюционной модели.
Заключение.
Итак, мы рассмотрели два типа моделей, отражающих причинно-следственные отношения в природе, проанализировали взаимную связь этих моделей, границы их применимости и некоторые особенности. Проявление причинности в природе многообразно и по форме, и по содержанию. Вполне вероятно, что этими моделями не исчерпывается весь арсенал форм причинно-следственных отношений. Но как бы ни были разнообразны эти формы, причинность всегда будет обладать свойствами объективности, всеобщности и универсальности. В силу этого принцип причинности выполнял и всегда будет выполнять важнейшие мировоззренческие и методологические функции в современном естествознании и философии естествознания.
Что касается постулата
о существовании "предельной скорости распространения взаимодействий",
это бессодержательное понятие внесло немало трудностей в физику. Можно
предположить, что это понятие возникло из-за необходимости придать некий глубинный
смысл релятивистскому множителю ![]() и оградить Специальную теорию
относительности от критики. Но эта попытка оказалась весьма неудачной. Понятие
"предельная скорость распространения взаимодействий" должно быть изъято
из физического лексикона.
и оградить Специальную теорию
относительности от критики. Но эта попытка оказалась весьма неудачной. Понятие
"предельная скорость распространения взаимодействий" должно быть изъято
из физического лексикона.
В силу сказанного, мгновенные взаимодействия могут существовать в природе, не нарушая принцип причинности, вопреки всяким догматическим "постулатам". Новое понимание причинности открывает путь для развития материалистической классической механики, квазистатических теорий взаимодействия зарядов в электродинамике и т.д.
Литература.
1. См., напр.: Г.А. Свечников Причинность и связь состояний в физике. М., 1971; Он же. Диалектико-материалистическая концепция причинности // Современный детерминизм: Законы природы / Под ред. Г.А. Свечникова и др. М., 1973. С. 125, и др.
2. См., напр.: В.С. Тюхтин Отражение, системы, кибернетика. М., 1972; А.И. Уемов, С.В. Остапенко. Причинность и время // Современный детерминизм: Законы природы. С. 214; 3.М. Оруджев, М.Д. Ахундов. Временная структура причинной связи // Филос. науки. 1969. № 6. С. 63; Жаров А.М. Временное соотношение причины и следствия и неопределенность // Там же. 1984. № 3. С. 89.
3. Кузнецов И.В. Избранные труды по методологии физики. М., 1. 975.
4. Материалистическая диалектика: В 5 т. Т. 1: Объективная диалектика / Под общ. ред. Ф. В. Константинова и В. Г. Марахова; Отв. ред. Ф. Ф. Вяккерев. М., 1981. С. 212.
5. Кузнецов И. В. Указ. соч. С. 237.
6. О парадоксах "нетранзитивности" см.: Н.3. Налетов Причинность и теория познания. М., 1975.
7. Г.В.Ф. Гегель Энциклопедия философских наук: В 3 т. Т. 1: Наука логики. М., 1974. С. 335.
8. Под термином "состояние" мы понимаем количественную и качественную определенность самодвижения объекта. Другие определения см.: В.П. Старжинский. Понятие "состояние" и его методологическая роль в физике. Минск, 1979.
9. В.Г.Иванов. Причинность и детерминизм. Л., 1974.
10. Материалистическая диалектика. Т. 1. С. 213.
11. М.Бунге. Философия физики. М., 1975. С. 99.
12. Д.Бом. Причинность и случайность в современной физике. М., 1959.
13. В.Я.Перминов. Проблема причинности в философии и естествознании. М., 1979. С. 209.
КРИЗИС РЕЛЯТИВИСТСКИХ ТЕОРИЙ
Часть 4. Вариационный принцип релятивистских теорий.
Кулигин В.А., Кулигина Г.А., Корнева М.В.
Физический факультет, Воронежский госунивестет
Университетская пл. 1, Воронеж, 394693, РОССИЯ
E-mail: kuligin@ el.main.vsu.ru
Показано, что релятивистский интеграл действия не имеет экстремумов. Благодаря этому факту надежных уравнений движения и законов сохранения не существует в рамках релятивистских представлений.
Kuligin V.A., Kuligina G.A., Korneva M.V. It is shown that relativity action integral has no extremums. Owing to the fact effective equations of motion and reliable laws of conservation are not exist in framework of Relativity theories.
Введение
В современной физической литературе очень часто говорится о “блестящем математическом формализме”, положенном в основу релятивистских теорий и, в частности, в основу Специальной теории относительности (СТО). Механика СТО разрабатывалась как обобщение принципа Гамильтона для 4-пространства. Главная цель Части 4- провести математический анализ этого обобщения. Чтобы упростить анализ и показать читателям ясную картину проблемы, мы будем использовать только Декартовы координаты.
1. Классический интеграл действия.
Мы начнем с краткого описания классического интеграла действия, чтобы затем использовать его для сравнения с релятивистским интегралом действия. Классический интеграл действия имеет следующий вид:
![]() (1.1)
(1.1)
где L = K - U - функция Лагранжа для частицы, на которую действует внешнее поле; K - кинетическая энергия частицы и U - потенциальная энергия взаимодействия.
Интеграл действия имеет минимум, если интегрирование ведется вдоль траектории частицы. Другими словами, вариация интеграла действия dS, должна быть равна нулю вдоль ее траектории. Чтобы определить траекторию частицы мы должны получить из интеграла действия уравнение ее движения (уравнение Эйлера). Это уравнение ищется путем варьирования координаты частицы r так, чтобы выполнялось условие минимума интеграла действия (1.1): dS = 0. При этом время t рассматривается как постоянный параметр: dt = 0. Окончательная форма вариации интеграла действия имеет вид:
![]() (1.2)
(1.2)
Поскольку dr это произвольная переменная, условие dS = 0 выполняется, если равно нулю подынтегральное выражение.
![]() (1.3)
(1.3)
Известно, что уравнение (1.3) есть уравнение движения частицы. Интеграл действия имеет минимум, если траектория частицы описана этим уравнением.
2. Интеграл действия в Специальной Теории относительности.
Исторически математический формализм релятивистской механики строился по образу и подобию формализма классической, опираясь на принцип соответствия между релятивистской и классической механиками при v<<c и принцип наименьшего действия. При этом, по утверждению апологетов теории относительности, форма математических операторов и уравнений в релятивистской механике сохраняется, а при v<<c релятивистская механика должна переходить в классическую. Поэтому форма релятивистского интеграла действия должна быть подобна (1.1).
![]() (2.1)
(2.1)
где: L - функция Лагранжа для частицы, на которую действует внешнее поле; с - скорость света; xi- 4-координата частицы (ict, x, y, z); ui - 4-вектор скорости частицы.
![]() (2.2)
(2.2)
Известно, что 4-координата xi зависит от s, и при дифференцировании ее по s мы имеем 4-скорость частицы.
![]() (2.3)
(2.3)
Таким образом, параметр s должен играть ту же роль, что и параметр t в классической теории.
Изучая литературу, мы столкнулись с двумя вариантами построения интеграла действия релятивистской механики, которые будут рассмотрены ниже.
Первый вариант. Он изложен в [1], [2]. Здесь параметр s подобен параметру t в классической механике. При варьировании интеграла действия он остается неизменным (dds=0). В результате мы имеем уравнение движения частицы по форме полностью соответствующее классическому уравнению (1.3) (Приложение 1).
![]() (2.4)
(2.4)
Итак, внешняя форма соблюдена, и мы можем рассмотреть ее содержание на конкретном примере. Авторы [2] для заряда в магнитном поле предлагают следующее выражение функции Лагранжа:
![]() (2.5)
(2.5)
где: е и m заряд и масса заряда соответственно; Ai – 4-потенциал электромагнитного поля.
Используя уравнение (2.4), нетрудно найти следующее уравнение движения для заряда:
![]() (2.6)
(2.6)
Это и есть релятивистское уравнение движения, которое при v<<c переходит в известное классическое уравнение.
![]()
где А и j - потенциалы электромагнитного поля; v – скорость заряда.
Казалось бы, все прекрасно, но существует обстоятельство, свидетельствующее не в пользу этого варианта. В СТО есть одно важное тождество
![]() (2.7)
(2.7)
Учитывая это соотношение, можно показать, что выражение (2.5) фактически не соответствует своему классическому аналогу.
![]() (2.8)
(2.8)
Очевидно, что из него мы не можем получить уравнение движения (2.6).
Более того, мы можем записать много других новых функций Лагранжа, которые равны предшествующей функции Лагранжа (2.5), и из них мы можем получить много других различных уравнений движения. Например, пусть функция Лагранжа равна:
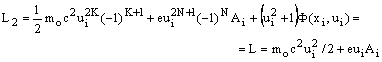 (2.9)
(2.9)
где: N и K - положительные целые числа (N,K = 0;1;2;…); Ф(xi;ui) - произвольная скалярная функция.
Теперь уравнение движения будет отлично от (2.6).
![]() (2.10)
(2.10)
Итак, мы можем получить много различных уравнений движения, изменяя K, N и Ф. Почему - это имеет место?
Возможно, что переменная s в СТО не может рассматриваться как независимая переменная подобно t в механике Ньютона. С одной стороны, s зависит от xi (2.2), с другой, xi должен зависеть от s (2.3). Благодаря этому, требование для вариационного исчисления нарушено. Как результат, рассмотренный вариант не может служить основой для математического формализма СТО.
Помимо этого, мы не можем получить классический интеграл действия при условии v<<c. Мы, например, имеем:
![]() (2.11)
(2.11)
Кинетическая энергия в 2 раза меньше необходимой.
Итак, первый вариант имеет следующие трудности:
1. Предельный переход от релятивистского интеграла действия к классическому не имеет места.
2. В отличие от классической механики релятивистский интеграл действия дает множество различных уравнений движения и неизвестно: какое из них отвечает объективной реальности?
Второй вариант. Другая версия интеграла действия приводится в учебнике [3]. Авторы [3] учитывают, что s зависит от xi. Они дают новый интеграл действия:
![]() (2.12)
(2.12)
Теперь правильный классический предел имеет место:
![]() (2.13)
(2.13)
Однако здесь мы сталкиваемся с другой проблемой. Новая общая форма уравнения движения отличается от классической (см. Приложение 1). Более того, нарушение единственности решения также имеет место
![]() (2.14)
(2.14)
Итак, второй вариант также имеет трудности:
1. Основная форма уравнения движения отличается от классической.
2. Мы имеем бесконечный ряд уравнений движения.
1. Ортогональность, но не произвольность.
Чтобы понять причины неудач релятивистского обобщения интеграла действия, рассмотрим общий вид вариации интеграла действия для двух вариантов.
Первый вариант [1], [2]. Он определяется условием δds=0.
![]() (3.1)
(3.1)
где ![]()
Проинтегрируем выражение (3.1) по частям.
![]() (3.2)
(3.2)
Первый член правой части равен нулю, поскольку концы траектории s1 и s2 жестко фиксированы и вариация в этих точках равна нулю по условиям вариации. Интеграл также равен нулю в силу соотношения δds=0.
Отсюда следует, что интеграл действия не имеет экстремумов. Его значение зависит только от пределов интегрирования и не зависит от формы траектории частицы. Принцип наименьшего действия не имеет места.
Второй вариант [3]. В этом варианте вариация δds≠0. Запишем вариацию интеграла действия для этого варианта.
![]() (3.3)
(3.3)
Как и в предыдущем случае, мы проинтегрируем первый член в интеграле действия по частям.
![]() (3.4)
(3.4)
Очевидно, что первый член правой части равен нулю по указанным ранее причинам, а второй тождественно равен нулю по результату интегрирования. Следовательно, для второго варианта справедливы те же выводы. Интеграл действия для второго варианта не имеет экстремумов. Его значение зависит только от пределов интегрирования и не зависит от формы кривой. Принцип наименьшего действия не имеет места.
Теперь нам необходимо
понять причину постоянства интеграла действия. Рассмотрим изменение длины
отрезка xi при бесконечно малой вариации δxi
и ![]() .
.
![]() (3.5)
(3.5)
Вычислим длину отрезков.
![]() (3.6)
(3.6)
С другой стороны, изменение 4-отрезка в рамках преобразования Лоренца не может быть произвольным. Существует жесткое условие:
![]() (3.7)
(3.7)
где αki - матрица преобразования Лоренца.
Из (3.7) следует, что длины сравниваемых отрезков должны быть равны друг другу, т.е. s(k)=s(i).
Сравнивая это соотношение с выражением (3.6), получим xiδxi=0. Иными словами, вариация δxi всегда должна быть ортогональна 4-вектору xi. Это соответствует обычному повороту 4-вектора в 4-пространстве или переходу 4-вектора из одной инерциальной системы отсчета в другую.
Пределы интегрирования s1 и s2 представляют собой две концентрических 4-поверхности, в которую "упираются" концы траектории частицы. При варьировании траектории эти концы свободно скользят по указанным поверхностям. В классическом интеграле действия концы траектории жестко "зафиксированы" в точках t1 и t2 .
Математический формализм Специальной теории относительности часто именуют "теорией инвариантов". Именно релятивистские инварианты должны быть слагаемыми релятивистской функции Лагранжа. Как известно, любой инвариант сохраняет неизменным свое значение при повороте в 4-пространстве (при переходе из одной инерциальной системы в другую). Следовательно, вариация любого инварианта, образованного 4-вектором, всегда ортогональна этому 4-вектору. Например, вариация квадрата 4-вектора скорости (инвариант) равна нулю.
![]() .
.
Таким образом, изменение релятивистского интеграла действия всегда равно нулю не в силу произвольности вариации, а в силу ортогональности 4-вариации уравнению движения. Это справедливо для каждого варианта.
Чтобы подтвердить этот вывод, запишем из [3] конечное выражение, из которого получают формулу Лоренца.
![]() (3.8)
(3.8)
Убедимся, что вариация интеграла равна нулю не в силу произвольности δxi.= ui δs, а в силу ортогональности уравнения движения (выражение в квадратных скобках) и δxi.
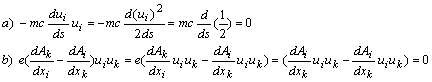
(3.9)
В выражение (3.9) входят скалярные слагаемые, и мы имеем право заменить одновременно индексы i на k, а k на i в первом слагаемом. Именно благодаря ортогональности мы получаем счетное множество уравнений движения, поскольку к любому уравнению движения мы можем добавить любой член, ортогональный к δxi. Вариация интеграла действия от этой процедуры не изменится и будет всегда равна нулю.
Обобщение. Рассмотренные выше выводы оказываются справедливыми и для интегралов действия, использующих плотность функции Лагранжа для получения уравнений полей.
![]() (3.10)
(3.10)
где: Λ - плотность функции Лагранжа; dΩ - элементарный 4-объем (dx·dy·dz·icdt).
Как мы писали выше, вариация любого инварианта, входящего в функцию Лагранжа, всегда ортогональна к вектору, образующему инвариант. Приведем примеры. Инвариант мы будем обозначать символом I.
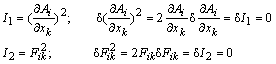 и т.д.
и т.д.
где Fik - тензор электромагнитного поля.
Неоднозначность уравнений движения можно проиллюстрировать, сравнивая вариацию одного и того же инварианта в разных формах его записи.
![]()
где jk не зависит от Ak .
Мы видим различные коэффициенты при произведении jk δAk.
Следовательно, уравнения для электромагнитных и гравитационных полей, которые были получены с помощью релятивистского принципа наименьшего действия, неоднозначны, а потому весьма сомнительны. "Блестящий математический формализм", которым всегда так гордились апологеты релятивистских теорий, на деле оказывается некорректным. Он напоминает "блестящий мыльный пузырь" благодаря математическим, физическим и гносеологическим ошибкам.
Заключение.
Вариация интеграла действия равна нулю в двух случаях. Во-первых, когда интегрирование идет вдоль экстремали, определяемой уравнением движения Эйлера. В этом случае интеграл имеет экстремум. Во вторых, когда величина интеграла постоянна. Она не зависит от пути интегрирования, а определяется только пределами интегрирования. Первый случай реализован в классической механике Ньютона. Второй - в релятивистских теориях.
Используя релятивистский интеграл действия и релятивистский принцип наименьшего действия, мы получаем счетное множество уравнений движения, и нет критерия, который бы позволил определить, какое уравнение отвечает физическим явлениям.
Используя этот интеграл и этот принцип, мы не можем достоверно сформулировать законы сохранения для релятивистской механики.
С помощью этого принципа невозможно получить единственные и надежные уравнения для электромагнитных и гравитационных полей.
Теории, опирающиеся на этот принцип, мягко говоря, сомнительны. Это релятивистская механика и электродинамика, Специальная и Общая теория относительности, различные струнные теории и т.д.
Учитывая гносеологические ошибки, внесенные Специальной теорией относительности А.Эйнштейна, мы можем сказать, что релятивистские теории представляют собой псевдонаучную эклектику.
Примечание. В работе [4] имеются ошибки. К счастью, они не имеют принципиального значения и не влияют на конечные выводы. В этой работе они исправлены.
Приложение 1. Доказательство нового уравнения движения.
Рассмотрим первый вариант. [1], [2].
![]() (A.1)
(A.1)
Учитывая, что δds=0, найдем
![]() (A.2)
(A.2)
Теперь, после интегрирования выражения (А.1) по частям, получим
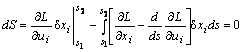 (А.3)
(А.3)
Первый член в правой части равен нулю, поскольку концы траектории закреплены и вариация в конечных точках должна быть равна нулю. В силу произвольности δxi выражение в квадратных скобках под интегралом должно быть равно нулю.
![]() (А.4)
(А.4)
Это есть уравнение движения для первого варианта.
Теперь рассмотрим второй вариант [3].
Запишем вариацию интеграла действия для этого случая.
![]() (А.5)
(А.5)
Сначала мы сделаем следующие промежуточные вычисления
a) ![]() (A.6)
(A.6)
b)
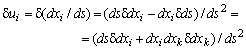 (A.7)
(A.7)
Учитывая (А.6) и (А.7), получим:
![]() (А.8)
(А.8)
После интегрирования выражения в круглых скобках в (А.8) по частям находим уравнение движения:
![]() (А.9)
(А.9)
Литература.
1. Г. Голдштейн. Классическая механика. – М.: Наука, 1975.
2. В.К.Пановски, М. Филлипс. Классическая электродинамика. - М: Мир, 1975.
3. Л.Д.Ландау, Е.М.Лифшиц. Теория поля. - М: Физматгиз, 1961.
4. В.А. Кулигин. Интеграл действия релятивистской механики./ Проблемы пространства, времени, тяготения. -С.-Петербург.: Политехника, 1997.
КРИЗИС РЕЛЯТИВИСТСКИХ ТЕОРИЙ
Часть 5.Электромагнитная масса.
Кулигин В.А., Кулигина Г.А., Корнева М.В.
Физический факультет, Воронежский госунивестет
Университетская пл. 1, Воронеж, 394693, РОССИЯ
E-mail: kuligin@ el.main.vsu.ru
Дано решение проблемы электромагнитной массы в рамках механики Ньютона. Показано, что любая масса имеет стандартные свойства механической массы.
Kuligin V.A., Kuligina G.A., Korneva M.V. The solution of the electromagnetic mass problem is given in framework of Newton's mechanics. It is shown that any mass has standard mechanical properties.
Введение.
Сразу же после доказательства Пойнтингом своего закона сохранения энергии возникла проблема электромагнитной массы. Причина в том, что электромагнитная масса не имела стандартных свойств обычной инерциальной массы. Ниже мы покажем это на примерах. Поскольку инерциальная масса любой заряженной частицы есть инерциальная масса со стандартными инерциальными свойствами, возникла гипотеза о том, что общая (механическая) масса заряда есть сумма электромагнитной массы и массы неэлектромагнитного происхождения. Хотя сам подход не вызывает сомнения, однако существует одна проблема. Электромагнитная масса, обладающая "плохими" свойствами, в сумме с массой неэлектромагнитного происхождения, также обладающей другими "плохими" свойствами, должна давать инерциальную массу с "хорошими" механическими свойствами. Это первый аспект.
Вторым аспектом проблемы электромагнитной массы стала проблема структуры протяженного заряда. Очевидно, что без решения первой проблемы решить вторую проблему нереально. Поиски модели заряда не привели к успеху [1], [2]. Предполагалось, что эти проблемы могут быть успешно решены с помощью квантовых теорий. Это предположение не оправдалось. Более того, оказалось, что многие трудности квантовых теорий имеют "классические корни". Проблема электромагнитной массы - один из таких корней.
Итак, мы имеем дело с порочным кругом. Выход нам подсказывают результаты, полученные в предыдущих Частях нашей работы. Во второй Части мы показали, что вектор Пойнтинга не универсален, электродинамика не может обойтись без уравнения Пуассона, а в третьей Части было установлено, что мгновеннодействующие потенциалы не противоречат принципу причинности.
Наша задача - анализ первого аспекта проблемы электромагнитной массы.
1. Проблема электромагнитной массы.
Мы не отрицаем, что применение вектора Пойнтинга к задачам, связанным с излучением и распространением электромагнитных волн, было плодотворным. Однако, мы должны, используя примеры, показать, что использование вектора Пойнтинга для анализа квазистатических явлений электродинамики ведет к некорректным результатам.
Как известно, масса частицы m в механике Ньютона связана со своим импульсом P соотношением:
![]()
Точно такое же соотношение должно иметь место и для плотности энергии частицы w и плотностью потока S.
![]()
![]() (1.1)
(1.1)
Мы предполагаем, что теми же свойствами должна обладать и плотность электромагнитной энергии.
![]() (1.2)
(1.2)
где ![]() - плотность энергии
электромагнитной массы.
- плотность энергии
электромагнитной массы.
Мы не будем рассматривать релятивистский случай, поскольку, как было установлено в Части 1, Специальная теория относительности не может рассматриваться как научная теория, а скорость зарядов не ограничивается скоростью света в вакууме.
Пример 1. Рассмотрим равномерно заряженную по объему сферу, движущуюся с постоянной скоростью вдоль v оси x. Для сравнения рассмотрим две точки на поверхности сферы, изображенной на рис. 1.
Вычислим величину вектора Пойнтинга для двух точек, одна из которых находится на максимальном удалении от оси, другая - на оси x.
![]() (точка 1)
(точка 1)
![]() (точка
2)
(точка
2)
Величина плотности массы (энергии) электромагнитного поля и величина скорости в этих точках одинаковы. Однако на периферии плотность потока Se в два раза больше, чем это требуется ньютоновской механикой, а на оси равна нулю. Почему такое различие?
В релятивистском случае мы сталкиваемся с известной проблемой “4/3”, которая обсуждается во многих учебниках по электродинамике (например, [3]).
Пример 2. Теперь мы рассмотрим бесконечную заряженную плоскость, которая изображена на Рис. 2. Если плоскость движется вдоль оси y, то плотность потока вновь в 2 раза больше.
![]()
Рис.1. Рис. 2 .
Здесь мы опять сталкиваемся с нарушением классического соотношения (1.2). Плотность потока в 2 раза больше требуемой. Если же плоскость перемещается вдоль оси x, то Se равно нулю, поскольку магнитное поле благодаря симметрии будет отсутствовать.
![]()
Как известно, в природе масса есть скалярная величина. Теперь мы должны признать, следуя логике, что скалярная инерциальная масса должна иметь тензорные свойства? Это абсурд! Некоторые исследователи считают этот пример некорректным, поскольку бесконечных заряженных плоскостей не существует. Тогда электродинамика должна иметь пределы применимости, т.е. должна содержать требование, чтобы исследователи не "забредали" в область тел больших размеров. Неужели там "другая" электродинамика? Нет, та же самая.
2. Вектор Умова.
Теперь мы будем решать эту проблему в рамках мгновеннодействующих потенциалов, поскольку принцип причинности позволяет нам этот шаг (см. Часть 3). В Части 2 мы высказали предположение, что поля зарядов и электромагнитная волна имеют различные свойства и, соответственно они должны описываться разными уравнениями. Запишем теперь уравнения для квазистатического поля заряда в привычной для нас форме. Здесь следует заметить, что из-за ошибочности Специальной теории относительности и ограниченности преобразования Лоренца мы не имеем ограничений скорости движения заряда. Эта скорость может быть любой.
![]() (2.1);
(2.1); ![]() (2.2);
(2.2); ![]() (2.3)
(2.3)
где ![]()
При этом векторный потенциал А связан со скалярным f так же, как плотность тока связана с плотностью заряда.
![]() (2.4);
(2.4); ![]() (2.5)
(2.5)
Эти дополнительные уравнения (2.4) и (2.5) будут необходимы нам для последующего анализа.
Нам необходимо показать, что уравнения (2.1), (2.2) и (2.3) соответствуют классической механике. Для реализации этой цели мы выразим векторный потенциал A в уравнении (2.1) через скалярный потенциал f , используя уравнения (2.4) и (2.5).
![]() (2.6)
(2.6)
В механике сплошных сред существует уравнение сохраняемости вектора а и интенсивности его векторных трубок [4], которое записано ниже:
![]()
Если в нем мы заменим вектор а вектором Е=-grad f/c2, тогда мы получим уравнение (2.6) для свободного заряда. Подобным образом из уравнения (2.3) мы получаем уравнение непрерывности, использующееся в механике сплошных сред.
![]() (2.7)
(2.7)
Уравнение (2.2) определяет потенциал f , создаваемый источником с обильностью ρ/ε.
![]() (2.8)
(2.8)
Мы видим, что квазистатическая электродинамика и механика сплошных сред имеют общие уравнения. Это рождает надежду найти решение первого аспекта проблемы электромагнитной массы. Решение проблемы электромагнитной массы было опубликовано нами в работе [5]. Теперь мы приступим к доказательству.
Доказательство.
Пусть потенциал f создается источником с обильностью ρ/ε (2.8). Запишем интеграл I.
![]() (2.9)
(2.9)
где dV - элементарный объем.
Используя теорему Гаусса, преобразуем интеграл I.
![]() (2.10)
(2.10)
где: dσ - элемент поверхности; nо-единичная нормаль к поверхности.
С другой стороны, используя уравнения (2.6) и (2.7) , мы можем представить уравнение (2.9) в следующей форме.
![]() (2.11)
(2.11)
Сравнивая уравнение (2.10) с (2.11), получим:
![]() (2.12)
(2.12)![]()
где: Su - плотность потокам вектора Умова
![]() (2.13)
(2.13)
![]() - плотность энергии поля
заряда (2.14)
- плотность энергии поля
заряда (2.14)
Уравнение (2.12) есть закон сохранения энергии Умова, который был опубликован им [6] еще в 1874 для механики сплошных сред. Другое доказательство закона сохранения энергии Умова было изложено в [5].
Очевидно уравнения (2.13) и (2.14) прекрасно соответствуют соотношениям механики Ньютона (1.1) и (1.2). Используя этот результат, мы можем дать корректное вычисление электромагнитной массы, которое устраняет трудности в рассмотренных ранее примерах. Полученные соотношения справедливы для зарядов произвольной формы.
![]()
3. Уравнение баланса кинетической энергии.
Теперь мы докажем другой важный результат: уравнение баланса кинетической энергии. Вряд ли вызовет сомнение факт, что электромагнитное поле обладает кинетической энергией. Однако мы приведем доказательство, чтобы дать полную картину явлений.
Сначала мы рассмотрим физическую модель кинетической энергии поля заряда. Если на заряд воздействуют внешние силы, заряд ускоряется, и кинетическая энергия поля заряда изменяется. Это изменение связано с изменением плотности тока j и векторного потенциала А.
Ускоренное движение заряда мы можем рассматривать как скачок заряда из одной сопутствующей инерциальной системы отсчета в другую. Сопутствующая и ускоренная системы отсчета имеют равные скорости в бесконечно малом интервале времени.
Электрическое поле E = - grad f в сопутствующей системе не зависит от времени и векторный потенциал A равен в ней нулю. Ускоренное движение заряда возбуждает добавочное электрическое поле E`, которое обусловлено изменением векторного потенциала А во времени (см. Приложение 1). Это поле мы не можем рассматривать как пренебрежимо малую величину. В сопутствующей системе отсчета оно равно:
![]() (3.1)
(3.1)
Плотность мощности, которая ускоряет заряд, равна:
![]() (3.2)
(3.2)
где μ*е плотность электромагнитной массы.
Эта мощность не зависит от выбора инерциальной системы отсчета в механике Ньютона.
Теперь мы должны описать эту модель математически.
Доказательство.
Для доказательства уравнения баланса кинетической энергии воспользуемся формулой Грина для векторного потенциала.
![]()
где: E и M - некоторые произвольные вектора полей.
Пусть ![]() будет полем, которое
создается ускоренным зарядом, а
будет полем, которое
создается ускоренным зарядом, а ![]() . В этом случае мы автоматически
получаем уравнение баланса кинетической энергии в стандартной форме:
. В этом случае мы автоматически
получаем уравнение баланса кинетической энергии в стандартной форме:
![]() (3.3)
(3.3)
где:
а) ![]() (3.4)
(3.4)
это плотность мощности, которая изменяет кинетическую энергию заряда;
б)![]() (3.5)
(3.5)
это плотность
кинетической энергии: ![]() ;
;
в) ![]() (3.6)
(3.6)
это плотность потока кинетической энергии.
Теперь необходимо проиллюстрировать этот закон на примере.
4. Баланс энергии элемента тока.
В квазистатической электродинамике векторный потенциал элемента тока определяется выражением:
![]() (4.1)
(4.1)
Подставляя выражение (4.1) в уравнения (3.6) и (3.8), мы можем записать такие результаты.
1.Плотность кинетической энергии равна:
![]() (4.2)
(4.2)
Распределение энергии обладает радиальной симметрией.
2. Плотность потока кинетической энергии равна:
![]() (4.3)
(4.3)
Теперь нам следовало бы обсудить особенности плотности потока кинетической энергии d2Sk
а) Изменение плотности кинетической энергии d2wk,, окружающей элемент тока, связано с плотностью потока кинетической энергии d2Sk. Плотность потока d2Sk , в свою очередь, зависит от изменения квадрата силы тока I во времени. Если величина тока (независимо от его направления) увеличивается, плотность потока кинетической энергии d2Sk положительна и d2Sk направлена вдоль радиуса. Она увеличивает энергию поля векторного потенциала, окружающего элемент тока. Если же ток уменьшается, тогда поток направлен к этому элементу тока. Он стремится поддержать и сохранить величину тока в этом элементе. При любом изменении величины тока потери на излучение отсутствуют. Заметим, что плотность потока d2Sk уменьшается в пространстве по мере удаления от элемента тока как 1/r3.
б) Когда изменение тока имеет место, плотность потока кинетической энергии возникает одновременно во всех точках пространства безо всякого запаздывания, т.е. мгновенно.
в) В противовес вектору Умова, который описывает конвективный перенос энергии зарядом, движущимся со скоростью v, плотность потока кинетической энергии существует только при ускоренном движении заряда (при изменении тока).
Электрическое поле,
равное ![]() , мы
можем рассматривать как напряженность поля, создающего ЭДС самоиндукции.
, мы
можем рассматривать как напряженность поля, создающего ЭДС самоиндукции.
Заключение.
Нами исследовалась проблема электромагнитной массы невзаимодействующего (свободного) заряда. При решении проблемы мы не использовали гипотез о строении зарядов. Электромагнитная масса имеет стандартные свойства механической инерциальной массы.
Как известно, масса заряда mo складывается из электромагнитной массы me и массы неэлектромагнитного происхождения mn: mo = me + mn . С помощью метода индукции несложно сделать важное обобщение. Любая инерциальная масса должна обладать стандартными свойствами механической инерциальной массы независимо от природы этой массы. Это очень важный результат.
Как предполагалось в Части 2, электродинамика имеет дело с двумя видами полей: с квазистатическими мгновеннодействующими полями зарядов (уравнение Пуассона, вектор Умова, инерциальная масса покоя заряда и т.д.) и электромагнитными волнами (волновое уравнение, вектор Пойнтинга, нулевая масса покоя поля и т.д.). Используя только запаздывающие потенциалы, мы не сможем построить правильную картину мира. Более того, можно предположить, что квантовые свойства заряда могут быть описаны и объяснены в рамках классических представлений. Непознаваемость явлений микромира с классических позиций есть уступка кантовскому агностицизму. Корпускулярно-волновой дуализм - не решение проблемы, а имитация решения. С этих позиций задача определения структуры протяженных частиц становится первостепенной задачей.
Приложение.
Запишем интеграл действия частицы, на которую воздействуют потенциальные силы. Все точки заряда движутся с одинаковыми скоростями.
![]() (A.1) где:
(A.1) где: ![]() ;
;
![]() - плотность
электромагнитной массы;
- плотность
электромагнитной массы; ![]() - плотность неэлектромагнитной массы.
- плотность неэлектромагнитной массы.
Из уравнения (A.1) следует уравнение движения.
![]() (A.2)
(A.2)
a) Пусть внешние силы отсутствуют (Λ=0). Частица будет устойчива, если выполняется следующее условие:
![]()
![]() (A.3)
(A.3)
б) Если же внешние силы существуют (Λ≠0), тогда мы можем предположить, что частица устойчива и выражение (А.3) применимо к ней.
Умножим выражение (A.2) на скорость v. Используя тождество (A.3), запишем произведение
. ![]()
![]() (A.4)
(A.4)
Первый член в выражении (A.4) есть электромагнитная плотность мощности ускоренной частицы (см. (3.4)).
![]() (A.5)
(A.5)
Напомним, что ρ и f не зависят от времени в собственной системе отсчета. Частица устойчива.
Литература.
1. Р.Ф.Фейнман, Р.Б.Лейтон, М.Сандс. Фейнмановские лекции по физике. Т.6, Электродинамика. -М.: Мир. 1975.
2. Д.Д.Иваненко, А.А.Соколов. Классическая теория поля. -М.: Наука. 1949.
3. В.К.Пановски, М.Филлипс. Классическая электродинамика. -М.: Мир, 1975.
4. Н.Е.Кочин. Векторное исчисление и начала тензорного исчисления. -М.: Наука 1965.
4. В.А.Кулигин, Г.А.Кулигина. Механика квазинейтральных систем заряженных частиц и законы сохранения нерелятивистской электродинамики. Воронеж. ун-т, Воронеж. Деп. в ВИНИТИ 09.04.1986, № 6451-В86.
6. N.A.Umoff (Umov). Beweg - Gleich. d. Energie in contin. Korpern, Zeitschriff d. Math. and Phys. V. XIX, Schlomilch. 1874.
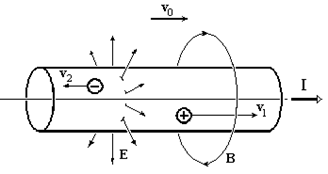
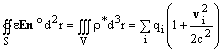 (2.2)
(2.2)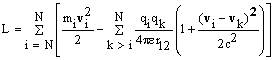 (3.6)
(3.6)
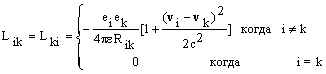
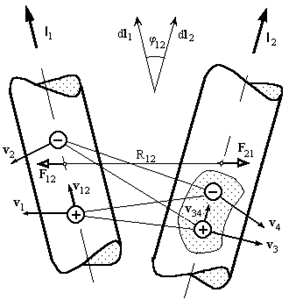
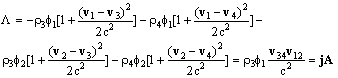 (6.1)
(6.1)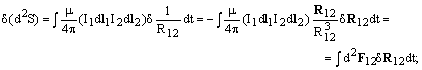
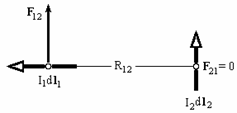
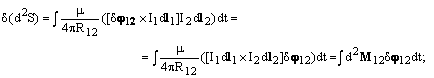
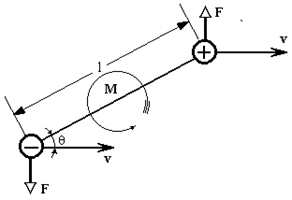
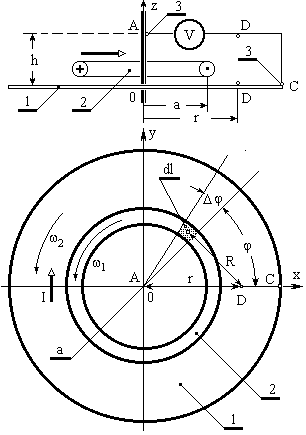
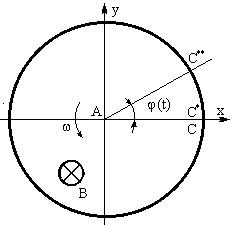
 (9.13)
(9.13) , где
, где