Динамические диаграммы Минковского: обмен сверхсветовыми сигналами
Относится к разделу Наука
Динамические диаграммы Минковского: обмен сверхсветовыми сигналами
Minkowski’s dynamic diagrams: exchanges of signals faster than light
Putenikhin P.V.
С 1908 года диаграммы Минковского используются для наглядной демонстрации различных ситуаций в рамках специальной относительности. По сравнению с аналитическими выкладками диаграммы позволяют более отчётливо увидеть кинематические эффекты теории. Следующим шагом повышения наглядности представления релятивистских эффектов следует считать их анимационное представление, показ этих эффектов в движении, в динамике. Для этих целей диаграммы могут быть представлены как в классическом виде, так и с динамическим масштабированием. В последнем случае масштаб диаграммы непрерывно увеличивается с течением времени, в результате чего появляется возможность рассматривать неограниченные временные и пространственные интервалы. В данной работе мы воспользуемся первым, классическим вариантом динамических диаграмм Минковского, с неизменным масштабом.
Ситуация, которую мы будем рассматривать, относится к довольно спорной области теории относительности – обмену сверхсветовыми сигналами. Носителями таких сигналов могут быть частицы из семейства тахионов, квантино (предложен Вейником), информион (так может быть названа частица, передающая квантовую информацию при коллапсе запутанных частиц), ньютион (такое название частице можно дать, чтобы подчеркнуть её антагонизм специальной теории относительности). Суть сверхсветового агента не важна. Единственное важное для нас его свойство – это его способность быть зарегистрированным в процессе сверхсветового движения.
Сначала давайте посмотрим на один из вариантов анимированных диаграмм Минковского для трёх различных случаев обмена сигналами между движущимися системами отсчета, а затем дадим описание всем изображённым на них элементам. Следует отметить, что динамические диаграммы выполнены в формате gif-файлов с оптимизацией в целях уменьшения их объёма. К сожалению, такие оптимизированные файлы некоторыми браузерами отображаются не вполне корректно. Например, браузер Интернет-эксплорер версии 8 и 9 «смазывает» изображение и замедляет его отображение. Но браузеры ИЕ-11 и firefox отображают эти динамические файлы без каких-либо дефектов. Поэтому, если отображение происходит со «смазыванием», то следует воспользоваться другим браузером. Все анимационные файлы «зациклены», то есть воспроизводятся повторно неограниченно долго, что позволяет внимательно рассмотреть и описать все происходящие на них процессы.
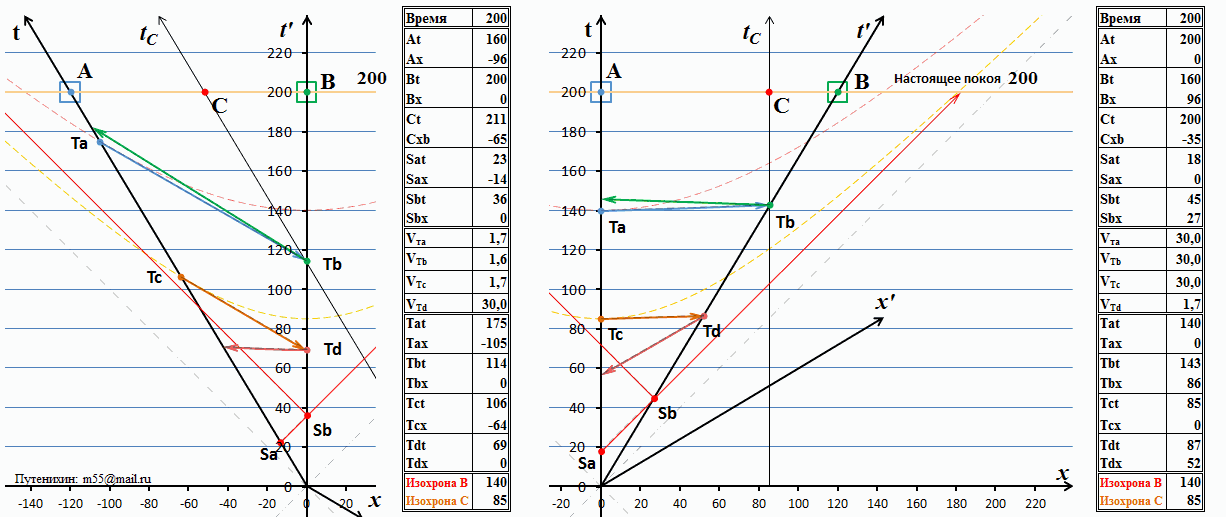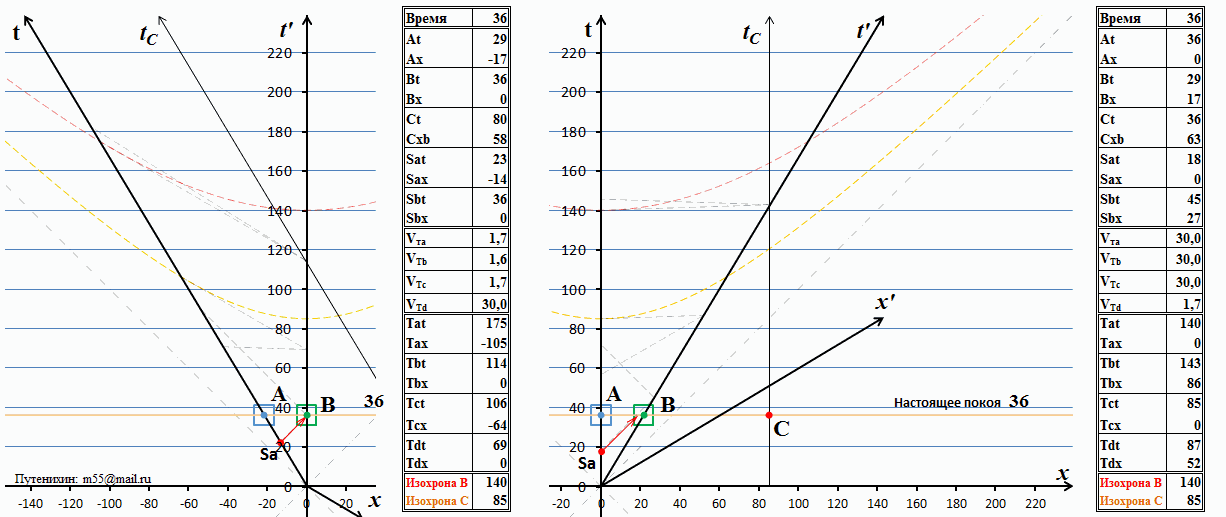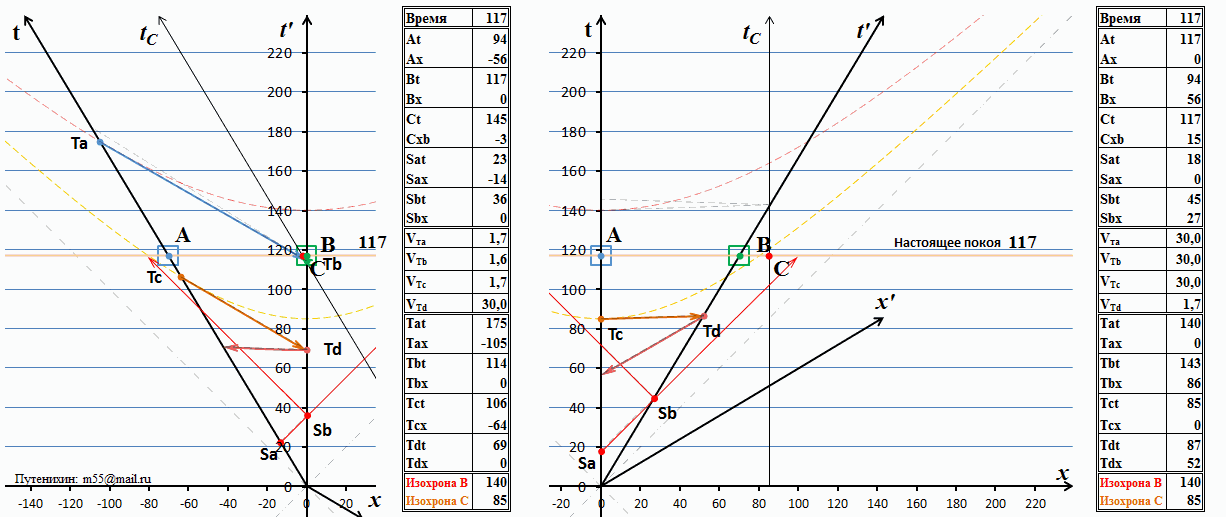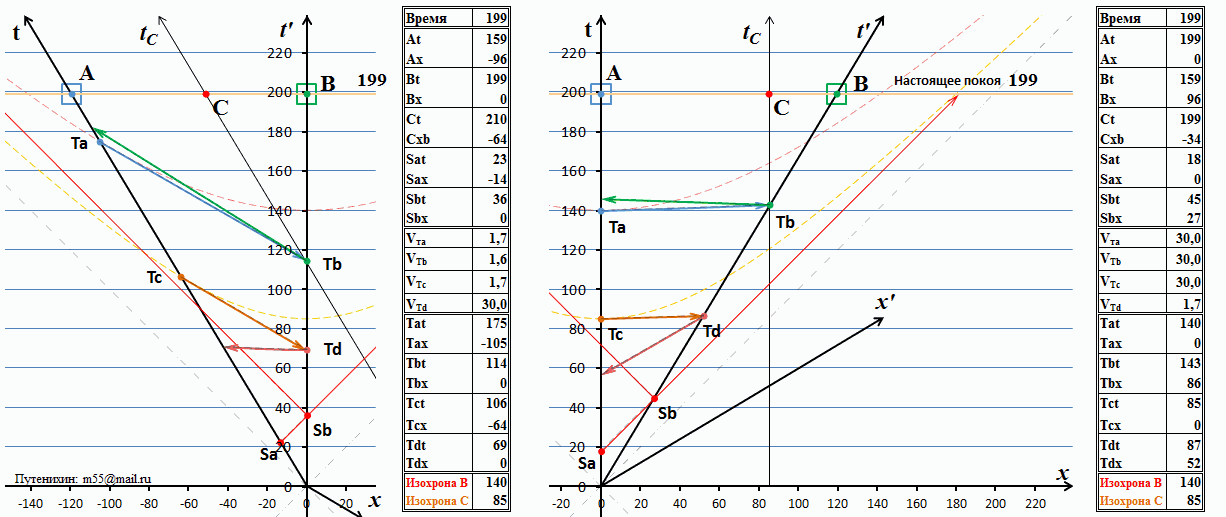
Рис.1 Динамические диаграммы Минковского для случаев обмена световыми и сверхсветовыми сигналами. Приведены диаграммы с точки зрения двух наблюдателей: слева – система покоя наблюдателя B, справа – наблюдателя A.
На диаграммах координатные оси имеют градации в долях от скорости света в системе единиц, в которой сама скорость света приравнена единице, то есть c=1. По этой причине вертикальная ось диаграмм имеет обозначение t вместо классического обозначения ct. Однако, размерностью этой оси являются, тем не менее, не секунды, а метры, хотя ось и обозначена как ось времени (м/сек * сек = м). Все уравнения Лоренца при таком значении скорости света записываются в более простой форме, без многоэтажных дробей. При этом скорости всех объектов будут измерять в долях скорости света. Например, классические уравнения преобразований Лоренца примут следующий вид:
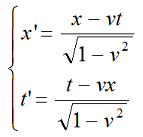
Понятно, что в этом случае абсолютное значение скорости для движущихся объектов будет не больше единицы. На диаграммах показано относительное движение двух систем отсчета – А и В. Слева на рисунке ситуация изображена с точки зрения системы В, которая в данном случае является лабораторной, условно неподвижной ИСО. Справа на рисунке системой покоя является система А. В рассматриваемом случае мы задали скорость относительного движения систем равной 0,6с или, для принятых допущений, просто 0,6. Эта скорость интересна с той точки зрения, что значение корня оказывается в точности равным 0,8.
Диапазон рассматриваемого на диаграмме движения составляет 220 секунд, а расстояния – чуть более 220 световых секунд. Световая секунда, как можно догадаться, это расстояние, которое свет проходит за 1 секунду, это примерно 70 миллионов километров. Картина ничуть не изменится, если принять, что оси размечены в световых годах.
В системе отсчета А находится вспомогательный наблюдатель С, который, понятно, является неподвижным в этой системе. Движение всех наблюдателей в пространстве-времени Минковского описывается их мировыми линиями. На рисунке таких линий три. Мировую линию системы А мы обозначим осью t. По этой причине на рисунке справа она строго вертикальна, ведь движения в собственной, связанной с ней самой системе у неё нет. Такой же вертикальной линией (на рисунке она имеет координату 85 световых секунд) является и мировая линия наблюдателя С – tC. Напротив, на левой половине рисунка они наклонны.
Мировая линия движущейся системы отсчёта В изображена осью t’. Все движущиеся системы имеет угол наклона своих мировых линий к оси времени, тангенс угла которых в указанных координатах точно равен скорости движения этой системы. Для системы В тангенс угла наклона, как мы задали, равен 0,6 на правой стороне рисунка. На левой стороне такой наклон имеют мировые линии наблюдателей А и С.
Ещё две пересекающиеся мировые линии изображены на обеих сторонах рисунка черными тонкими штриховыми линиями. Это мировые линии света, они наклонены к вертикальным осям под углом в 45 градусов. В трёхмерном варианте диаграмм они образуют два так называемых световых конуса - будущего и прошлого. Мировые линии всех движущихся систем отсчета находятся внутри этих конусов.
Для удобства анализа состояния систем на диаграммах показаны также и другие вспомогательные линии. Основная из них – это линия «настоящее время системы покоя» или, кратко, «настоящее покоя». Эта линия изображена оранжевым цветом, надписью и числовым отображением времени, соответствующего настоящему времени системы покоя. Все события, которые могут произойти в неподвижной системе отсчёта могут находиться только на этой линии настоящего. Напротив, все события ниже этой линии уже произошли и находятся в прошлом. Все события выше этой линии ещё не произошли, они – события будущего.
На диаграмме красными тонкими штриховыми линиями изображены ещё две вспомогательные линии - изохроны и изотрасы. Это линии, соответственно, равных времён и равных расстояний. Они позволяют сравнить ход времени во всех системах отсчёта, нанесённых на диаграмму, обнаруживая при этом все лоренцевы кинематические эффекты: замедление времени, сокращение расстояний и относительность одновременности.
Справа от каждой диаграммы приведена таблица со значениями основных параметров движения систем и свершения событий. Заглавными буквами обозначены, соответственно, А, В и С – инерциальные системы отсчета одноименных наблюдателей. Индексы t и x означают соответствующую координату этих систем отсчета. В зависимости от диаграммы координаты времени отражают течение времени внутри системы с точки зрения неподвижной, лабораторной системы отсчета, если не указано иное для конкретной диаграммы. Для системы С представляют интерес и показаны на некоторых диаграммах только её координаты с точки зрения системы В, поскольку в системе А она неподвижна. Через V с индексами a, b, c и d обозначены скорости одноименных индексам тахионов. Через S с индексами a и b обозначены события излучения световых сигнала и ответа на сигнал, соответственно. Изохроны и изотраса обозначены координатами своих точек, ближайших к началу координатных осей. Для наглядности на некоторых диаграммах тонкими штриховыми линиями обозначены трассы сигналов – тахионов и света. Более подробно при необходимости эти значения мы опишем при рассмотрении отдельных моментов движения.
На показанной выше анимации динамических диаграммах Минковского можно выделить три отдельных, независимых процесса или этапа. Опишем эти процессы подробнее.
Обмен световыми сигналами между движущимися системами
Этот процесс является простой демонстрацией динамических диаграмм и не несёт особо сложной смысловой нагрузки:
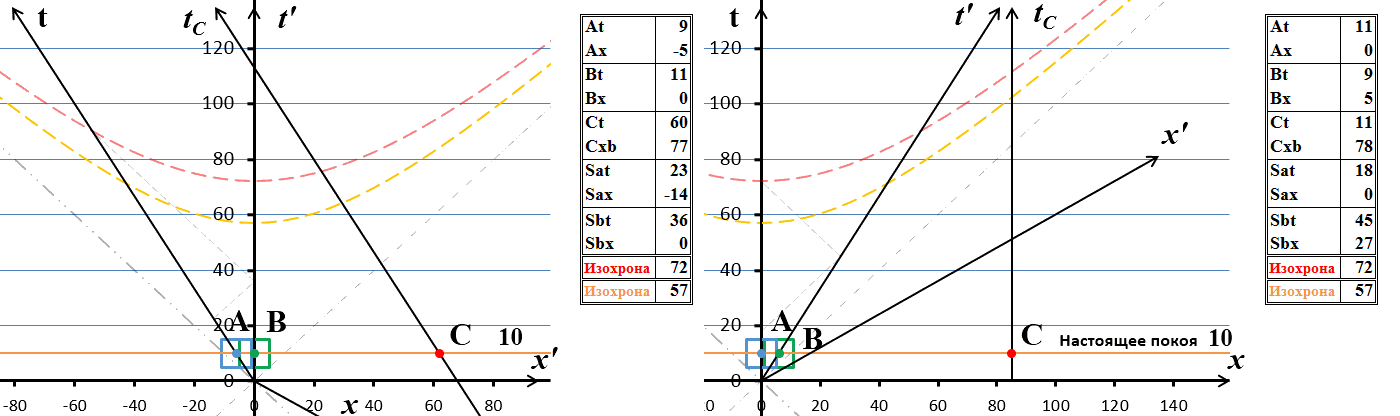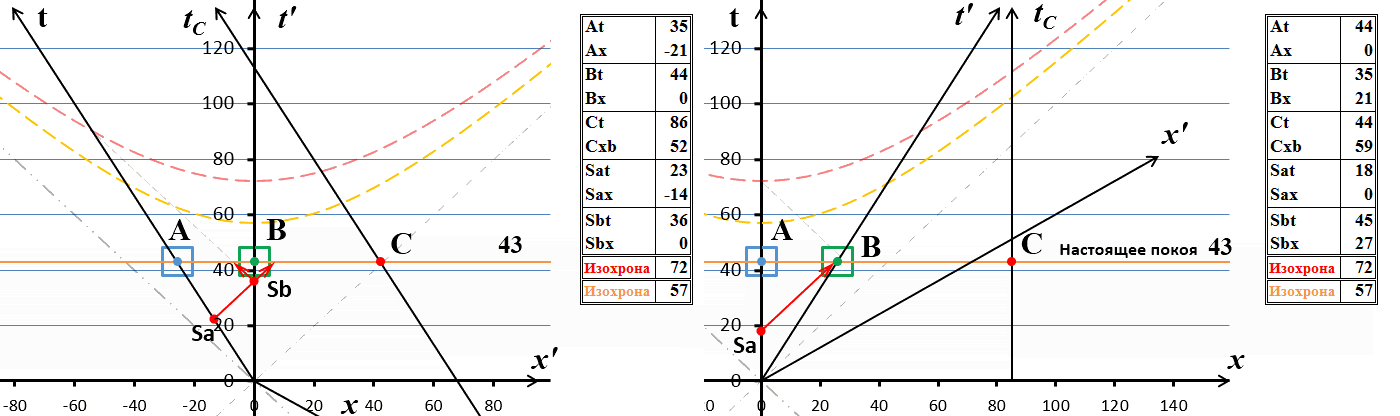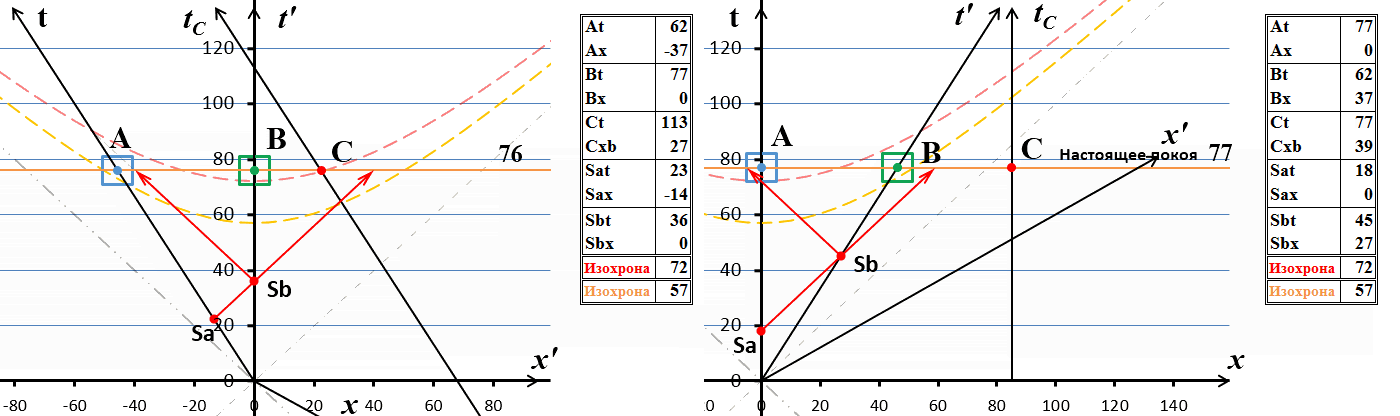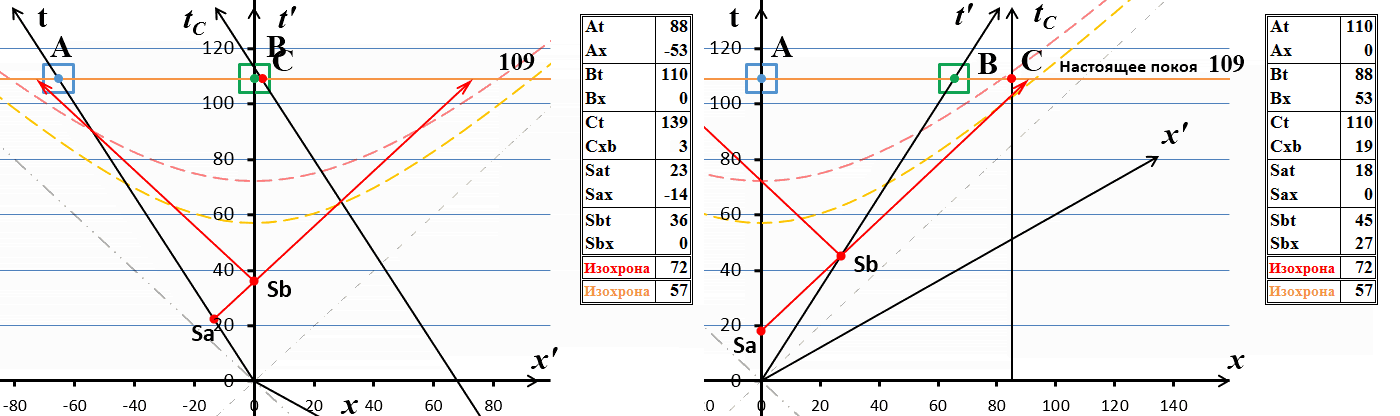
Рис.2 Обмен световыми сигналами между движущимися системами. Приведены диаграммы с точки зрения двух наблюдателей: на правой половине – с точки зрения системы покоя наблюдателя А, на левой – наблюдателя В.
На этих диаграммах оставлены только мировые линии световых сигналов, которые обозначены красными стрелками. В момент времени Sa=18с из неподвижной системы отсчета А излучается световой сигнал в сторону системы В. Когда сигнал в момент времени Sb=45с достигает системы В, оттуда излучается ответный сигнал, который, как можно увидеть на диаграмме, достигает системы А в момент времени примерно 72с, что видно по изохроне 72: точка её пересечения с мировой линией А показывает на последней время 72.
Далее основной и ответный сигналы продолжают свободное движение в пространстве, удаляясь от систем А и В в разные стороны. Например, в момент времени приблизительно 102с по собственным часам сигнал достигает третьего наблюдателя – С. Может возникнуть вопрос: приблизительно в этой точке мировую линию С также пересекает изохрона 72, почему же время события 102с, а не 72? Потому, что изохроны отсекают «своё время» только на мировых линиях, исходящих из начала координат.
Ситуация, как видим, является тривиальной, и весь смысл динамической диаграммы состоит в её наглядности. На этой диаграмме изохрона 72 совмещена с точкой получения системой А ответного сигнала. Поскольку изохрона – это линия равных времён, то в данном случае это означает, что по часам системы В поглощение произошло в 72с, в то время как по часам А – примерно в 90с. Это точно соответствует решению уравнений Лоренца:
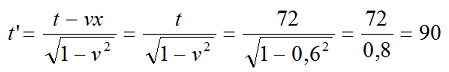
Если на рис.1 измерить отрезки, отсекаемые на оси x’ мировой линией tC и изотрасой, то можно найти, что с точки зрения подвижной системы В наблюдатель С находится от начала координат на расстоянии:
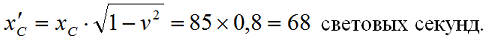
То же самое по точкам на диаграмме:
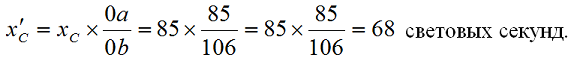
Нужно отметить, что мировые линии света имеют один и тот же неизменный наклон в обеих системах отсчета, то есть одну и ту же скорость. Это является отражением второго постулата специальной теории относительность об инвариантности скорости света во всех системах отсчета. Напротив, мировые линии движущихся систем отсчета изменяют свой наклон при переходе в другую систему отсчета.
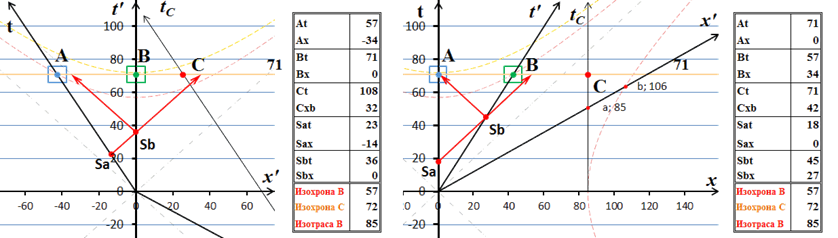
Рис.3 Обмен световыми сигналами между движущимися системами. Время прибытия ответного сигнала не зависит от точки зрения.
Обратите внимание на время регистрации ответного сигнала в системе А. На рисунке, казалось бы, несоответствие: с точки зрения системы А (справа) сигнал уже прибыл в неё, но с точки зрения наблюдателя В (слева) сигнал ещё в пути. Однако, никакого несоответствия нет. В лабораторной системе А сигнал зарегистрирован в 72 секунды по её часам. При этом часы системы В показывают с точки зрения А время 58 секунды. Если рассматривать ситуацию для этого же времени из лабораторной системы В на левой стороне рисунка, то мы видим, что часы А показывают с её точки зрения лишь 58 секунд. То есть по часам А ещё не наступило время регистрации ответного сигнала.
Обмен тахионными не-инвариантными сигналами
Практически с момента создания специальной теории относительности возник вопрос о возможности её применения к сигналам или объектам, движущимся быстрее скорости света. На первый взгляд кажется очевидным, что теория неприменима к таким сигналам. Тем не менее, основная масса физиков, в том числе и Эйнштейн, считают, что это не так, что нет принципиальных препятствий к такому расширению теории.
Вывод о предельности скорости света оказался прямым следствием её инвариантности. Именно вследствие инвариантности скорости света ни один другой объект не может превысить эту скорость. Но как тогда поступить с тахионом? Ведь у него скорость выше. Может быть это новый инвариант скорости? Нет, физики сошлись во мнении, что скорость тахиона, хотя и превышает скорость света, тем не менее инвариантом не является. Прямым следствием этого является то, что скорость тахионного сигнала, как и скорость любого классического досветового сигнала зависит от скорости источника. Другими словами, скорость движения тахиона складывается со скоростью его источника по релятивистскому правилу сложения скоростей.
На динамической диаграмме обмен такими тахионными не-инвариантными сигналами показан на примере двух сигналов: прямого – Tc и ответного – Td:
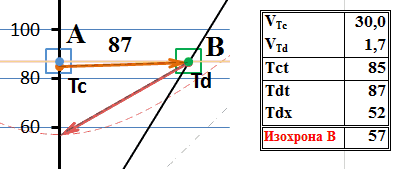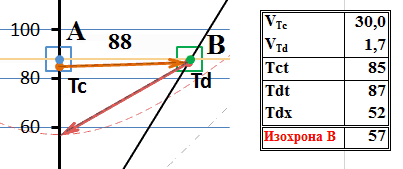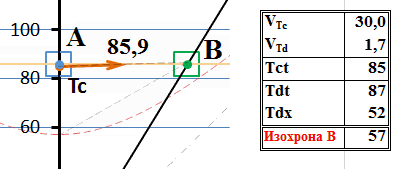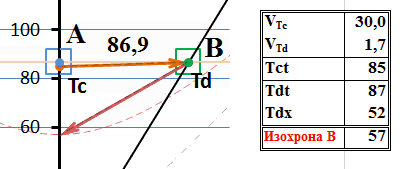
Рис.4 Обмен сверхсветовыми сигналами между движущимися системами
Скорость тахиона в неподвижной системе отсчета выбрана ограниченной, хотя существенно выше скорости света – 30с. Для графического изображения такая скорость является достаточным приближением к «бесконечно большой скорости». Вместе с тем, ограничение её величины позволяет на диаграмме слегка разнести траектории прямого и обратного сигнала, избежать их слияния. На приведенной диаграмме мировая линия такого тахиона практически параллельна горизонтальной оси, что означает одновременность моментов излучения и прибытия тахиона в движущуюся систему:
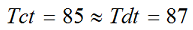
Как известно, передача информации со сверхсветовой скоростью приводит к различным акаузальным (нарушающим причинность) парадоксам в теории относительности. В частности наблюдаются эффекты «передачи сигнала в прошлое» и нарушение причинно-следственных отношений. На данном рисунке это хорошо заметно. Действительно, прибытие тахиона в систему В по её по часам произошло в 70 секунд, о чём свидетельствует изохрона С. Но испущен-то он был как бы позже, в 85 секунд! Конечно, это вряд ли свидетельствует о движении в прошлое, ведь эти часы относятся к разным системам и, что такое раньше или позже, относительно. Парадокс возникает при ответной отправке сигнала – из В в А. Здесь уже ответный сигнал фиксируется в той же самой системе отсчета, из которой испущен сигнал, по тем же самым часам. Ни о какой относительности теперь говорить нельзя. А ситуация, действительно, парадоксальная. Сигнал отправлен из А в 85 секунд, а ответный сигнал пришёл… в 57 секунд! Логика и здравый смысл подсказывают, что такого быть не может!
В чём же причина и как решить этот парадокс? Причина в том, что мы установили не-инвариантность скорости тахиона. То есть, его скорость в прямом направлении была бесконечной (близкой к ней), а вот обратная скорость – на порядок меньше, поскольку она сложилась по релятивистскому закону со скоростью отправителя – системы В – Vтахион_D=1,7. Действительно, вычислим эту скорость явно:
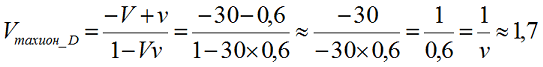
Здесь мы в процессе вычислений отбрасываем за малостью единицу в знаменателе, а в числителе по той же причине отбрасываем 0,6с. Как видим, скорость ответного тахиона лишь ненамного выше скорости света. Хорошо видно, что в общем случае, когда скорость тахиона существенно выше скорости системы отсчета и Vv>>1, результирующая скорость тахиона вообще не зависит от его «собственной» скорости, а определятся только скоростью источника:
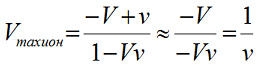
Чтобы показать странность ситуации, приведём забавное сравнение. Пуля из ружья неподвижного стрелка вылетает с высокой скоростью. А пуля, выпущенная тем же стрелком из движущейся повозки, буквально падает у его ног, причём хоть по ходу, хоть против хода движения. Это, действительно, странно.
На диаграмме можно заметить, что в случае равенства скоростей сигнального и ответного тахиона, то есть при параллельности их мировых линий, никаких «путешествий в прошлое» не было бы. Значит, к тахиону нельзя применять релятивистское правило сложения скоростей?
Мы рассмотрели ситуацию с точки зрения системы А. Но законы теории относительности позволяют и даже требуют рассмотреть эту же ситуацию и с точки зрения другой системы – В. Выглядит эта диаграмма так:
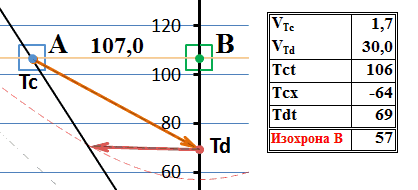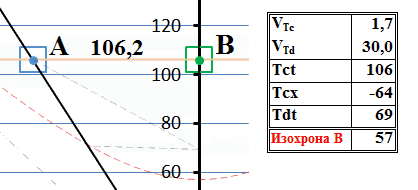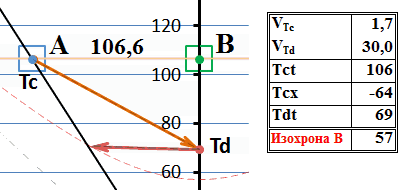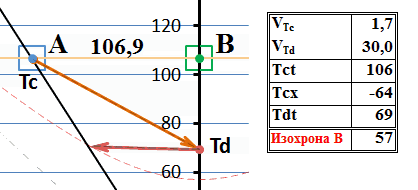
Рис.5 Обмен сверхсветовыми сигналами с точки зрения системы В
Теперь уже ответный тахион имеет бесконечно большую скорость. Однако, как и следовало ожидать, он всё равно прибыл в систему-отправитель сигнала раньше, чем оттуда был отправлен сигнальный тахион. И здесь видна та же особенность. Всё как бы склоняется к тому, что если бы скорость тахиона была инвариантом, то обмен сигналами произошёл бы «по горизонтали» или по параллельным мировым линиям и никакого движения в прошлое не было бы. Рассмотрим ситуацию более внимательно, на замедленной анимации вблизи точек испускания-поглощения сигнального тахиона в режиме анимации «пинг-понг»:
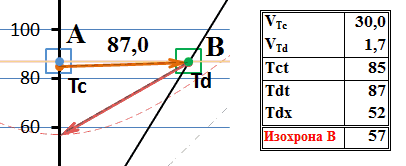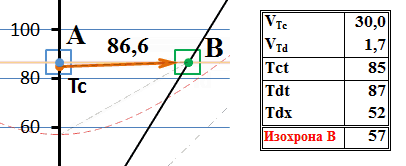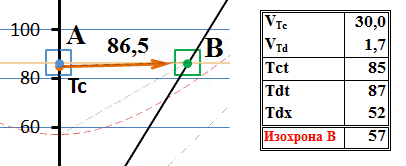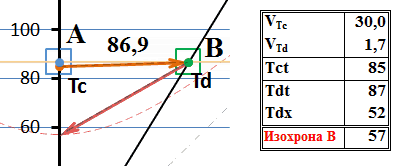
Рис.6 Обмен сверхсветовыми сигналами с точки зрения лабораторной системы А
Тахион из точки Тс движется к точке Td со скоростью 30 (скоростей света, напомним). Но, когда он её достигает, оттуда излучается тахион в прошлое. Такое «движение в прошлое» на диаграмме воспроизведено как мгновенное, и это весьма показательно. Хотя линия движения и обозначает скорость около 1,6с, но это скорость движения «в прошлое», в котором поглощение тахиона уже как бы свершилось, тахион, собственно говоря, находился там уже давным-давно. То есть, это, собственно и не движение, а как бы констатация факта, что по прибытии сигнального тахиона в В, ответный сразу же оказался, а правильнее сказать, обнаружился в прошлом системы А.
Как современная физика решает этот навязанный специальной относительности парадокс? Весьма оригинально. Изобретён так называемый «принцип реинтерпретации». Он гласит, что движущийся в прошлое тахион с положительной энергией должен рассматриваться как движущийся в будущее антитахион, то есть тахион с отрицательной энергией. К изобретению этого принципа причастны знаменитые физики, но, тем не менее, он также напрашивается на шуточную аналогию. В магазин заходит покупатель и отдаёт продавцу минус килограмм продуктов. Взамен продавец отдаёт покупателю минус 100 рублей.
Но насколько принцип реинтерпретации решает проблему сверхсвета? Допустим, с излучением сигнального сверхсветового тахиона дела обстоят боле-менее приемлемо. Да, он попадает в более раннее время получателя, чем свет. Но законам физики, логики и здравому смыслу это по большому счету не противоречит. Тахион движется строго в будущее, не «выпрыгивая» из настоящего. С получением тахиона, таким образом, тоже особых проблем не видно. Сначала излучатель излучил, затем получатель получил – всё соответствует причинно-следственным отношениям, ни у кого из них не должно возникать вопросов, откуда, что и почему.
Но возникает пара серьёзных вопросов, претензий к принципу реинтерпретации. Да, можно рассматривать «обратный» тахион как «прямой» антитахион. Но, тогда вопрос: кто его излучил? Тахион, как мы знаем, испущен источником. А кто излучил антитахион? Это вопрос, имеющий только один очевидный и бесспорный ответ: антитахиона никто не излучал. Следовательно, его нет и быть не может. Действительно, в момент времени 57 по собственным часам наблюдателя А из будущего должен был прибыть тахион, как показано стрелкой на рис.6. Но движение в прошлое отвергают даже сторонники принципа реинтерпретации. Именно поэтому и предложено рассматривать движение в будущее, но уже антитахиона. В этот момент времени 57 из этой точки, как утверждается, испущен антитахион. Абстрактно-неопределенное высказывание «испущен» требует уточнения: кем или чем испущен? Уйти от этого вопроса невозможно: если антитахион испущен, то обязательно должен быть излучатель, который его испустил. Нет и быть не может каких-либо разумных обоснований этого «никем и ничем» излучения. Принцип реинтерпретации здесь лишён смысла, он абсурден.
Теперь второй вопрос. Знал ли излучатель тахиона на момент его излучения что-нибудь о том, что ранее или одновременно c тахионом он излучил антитахион? Пока он не излучил тахион, никакого антитахиона не было. Но как только тахион ушёл к получателю, тут же, сразу излучатель вдруг неожиданно «вспомнил», что совсем недавно он точно так же излучил антитахион? Или он всё-таки не излучал антитахиона когда-то давно, а получил тот самый тахион, движущийся в прошлое? Ответ такой же: этого быть не может. Это точно такое же «никем и ничем» излучение антитахиона. Невозможно изобрести даже в малой степени разумное описание такого излучения. Даже движение в прошлое выглядит меньшим абсурдом, чем абсурдные доводы принципа реинтерпретации.
Но как же тогда объяснить наблюдаемое на диаграммах явление? Вывод напрашивается также очевидный и единственный. Специальная теория относительности не даёт и не может дать правильного решения для сверхсветовых движений. Они вне её компетенции. Если поменять тахион на сверхсветовую посылку, то отправитель, чтобы получить её в прошлом, сначала должен отправить её в будущем. И в полученной посылке вполне может оказаться подарок с наклейкой на корпусе: «Изготовлено в будущем году».
Обмен тахионными инвариантными сигналами
Выше мы обнаружили, что не-инвариантность скорости тахиона приводит к нарушению причинности и к «путешествиям в прошлое». А что будет, если скорость тахиона будет таким же инвариантом, как и скорость света? В принципе, такая ситуация может быть имитирована с помощью размещения источника и приёмника в одной и той же, неподвижной системе отсчета. В этом случае обратный тахионный сигнал движущаяся система отправляет не от себя, а запускает неподвижный передатчик такого сигнала, просто оказавшись в определенный момент рядом с ним.
Пусть такой передатчик находится в точке С. Когда в движущуюся систему В поступает сигнал из А, она «совершенно случайно» оказывается точно рядом с передатчиком С и отправляет с него ответный сигнал:
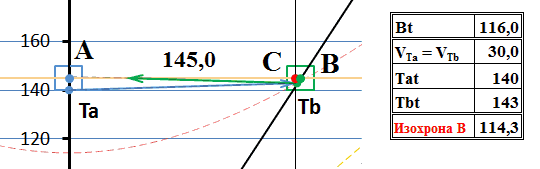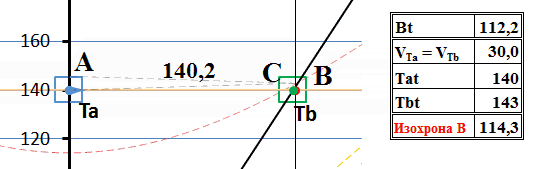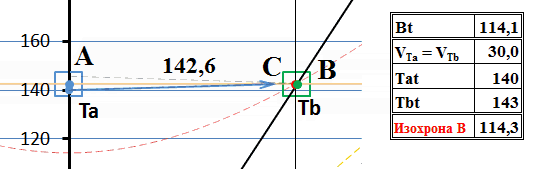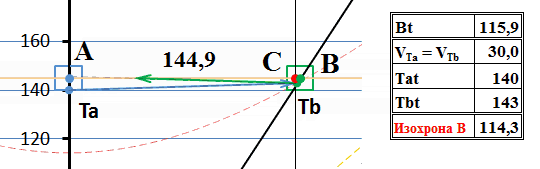
Рис.7 Процесс обмена тахионами с точки зрения системы А.
Как видим, в этом случае равной бесконечности становится скорость и обратного тахиона, поэтому он приходит к отправителю в тот же момент, что и отправленный тахион. Все движения тахионов происходят в одной и той же неподвижной системе отсчета, между двумя неподвижными наблюдателями А и С. Поскольку их относительная скорость равна нулю, преобразования Лоренца превращаются в преобразования Галилея и мгновенный обмен сигналами не вызывает в этой системе никаких парадоксов, никаких нарушений причинности и движения в прошлое нет. Это в неподвижной системе. А что при этом видит движущийся наблюдатель В?
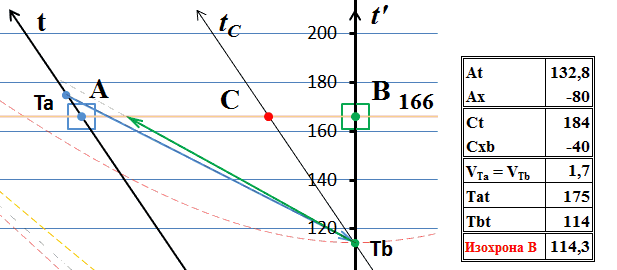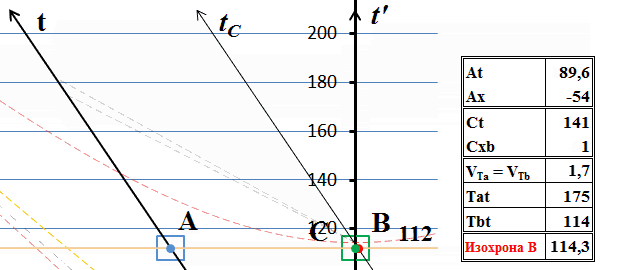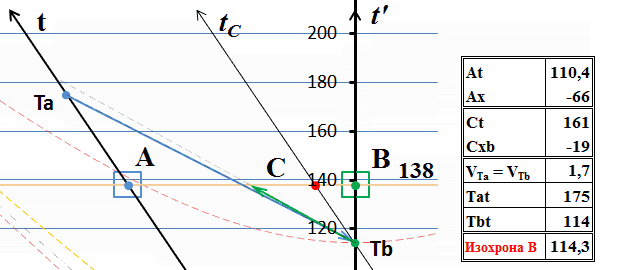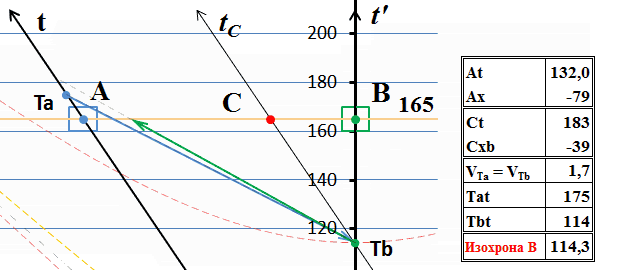
Рис.8 Процесс обмена тахионами с точки зрения системы В.
Движущийся наблюдатель В видит обратное движение во времени. Сигнальный тахион уже пришёл к нему, хотя он ещё не был испущен. То есть налицо факт предсказания событий: получатель может с уверенностью заявить, что из А будет в определенное время испущен тахион. Однако, это довольно специфическое предсказание. С одной стороны, предсказание в общепринятом смысле подразумевает возможность наступление события с некоторой вероятностью. Но в данном случае предсказание скорее является констатацией свершившегося факта, это предсказание достоверного события, которое наступит в обязательном порядке. Как только наблюдатель С регистрирует прибытие тахиона, сразу же достоверно становится известно событие будущего. Это, конечно же, предсказание, но оно имеет парадоксальные свойства – свершившееся событие - следствие как бы вызывает событие - причину в будущем. Это называется опережающей причинностью, которая приводит, назовём его так, к парадоксу предсказателя или «парадоксу оракула» специальной относительности. Конечно, в обыденной жизни мы сталкиваемся с похожими на первый взгляд предсказаниями. Например, мы можем с достоверностью предсказать, что завтра взойдёт Солнце. Но существует ненулевая вероятность того, что этого не произойдёт. В случае рассмотренного «парадокса оракула» такой вероятности нет: это своеобразное предсказание уже наступившего в будущем события.
С ответным сигналом всё обстоит нормально, если не учитывать, что сигнал-инициатор лишён физического смысла. Здесь, как и в предыдущем примере, принцип реинтерпретации даёт, казалось бы, приемлемое описание процесса. Если рассматривать не тахион, пришедший из будущего, а антитахион, движущийся нормально из настоящего в будущее, то всё вроде бы складывается. Но вновь тот же вопрос к принципу: кто является источником, инициатором антитахиона? И кто его получит, когда он формально достигнет излучателя А? В тот момент излучатель явно и определенно испустит тахион. При этом тахион будет двигаться строго по законам природы: из настоящего – в будущее, то есть вверх по диаграмме, но никак не в прошлое, вниз, как это показано голубой мировой линией. Движение в прошлое лишено физического смысла.
Итак, мы попытались установить скорость тахиона инвариантной, независимой от состояния движения наблюдателя. Но на диаграмме мы видим, что скорость тахиона все равно оказалась зависимой от скорости наблюдателя. Почему, ведь мы это задали как исходное условие? Дело в том, что одного только заявления «инвариант» недостаточно. Фактически мы следовали принципу относительности и «подтянули» точки излучения и получения тахионов к моментам времени, которые соответствуют другому, действительному инварианту – скорости света. Инвариантность скорости тахиона на этой диаграмме должна изображаться такими же горизонтальными мировыми линиями тахионов, как и на смежной диаграмме. Легко заметить, что в этом случае точка прибытия тахиона в В и точка излучения из него ответного тахиона окажутся разнесёнными во времени, они перестают быть одновременными событиями. Действительно, если мы изобразим на этой диаграмме мировые линии тахионов горизонтальными (толстые красные линии со стрелками), то они тогда в принципе не могут соединить две точки Ta и Tb, разнесённые по вертикали (во времени):
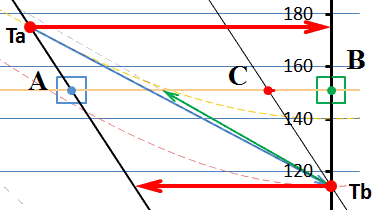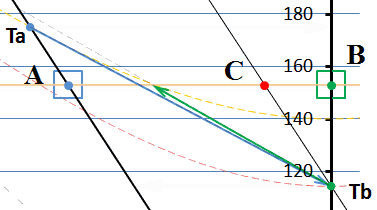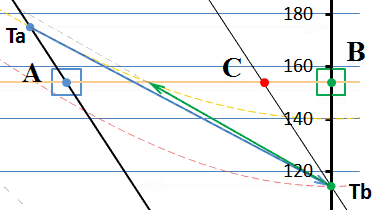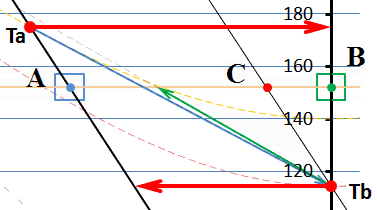
Рис.9 Приведение мировых линий тахионов к инвариантным
Если мировые линии каждого из тахионов мы изобразим горизонтальными линиями инвариантов, как показано на рисунке, то сигнальный тахион не попадает в приёмник, находящийся по вертикали ниже, а ответный тахион не попадает в излучатель, находящийся выше по горизонтали, хотя по условиям задачи тахион должен вернуться в излучатель. Цепочка событий во времени разрывается.
Собственно говоря, в этом и заключена основная суть инварианта скорости. Он «деформирует» пространство-время исключительно «под себя». Любая «деформация» пространства-времени под другой инвариант искажает первоначальную деформацию, разрушает исходный инвариант. Не может быть в одном и том же пространстве-времени одновременно двух инвариантов скорости. И из этого, как видим на диаграмме, следует, что скорость, превышающая скорость инварианта, неизбежно приводит к нарушению причинности в смысле последовательности событий во времени: становится невозможным совместить одновременные одноместные события в одной и той же точке пространства-времени. Такое нарушение последовательности событий во времени и выглядит как движение в обратном направлении времени.
Помимо проблемы с двойным инвариантом сверхсветовая скорость приводит и к другим парадоксальным следствиям. Вспомним логику формирования положений специальной теории относительности. Главным постулатом следует считать постулат об инварианте скорости света, именно он приводит к появлению всех кинематических эффектов теории – преобразований Лоренца. Во всех уравнениях Лоренца инварианту отводится строго определенное место, отличающееся от другой величины – скорости движущейся инерциальной системы отсчета. То есть, можно определенно заявить: в уравнениях Лоренца присутствуют две скорости – инвариантная скорость света и скорость движущейся системы отсчета:

Как мы видели, скорость тахиона в принципе не может быть инвариантом, пока им является скорость света. Двух инвариантов скорости быть не может, как невозможно подставить в одно и то же место уравнения два разных значения одновременно. В теории относительности нет других объектов: только инвариант и системы отсчета. Следовательно, скорость тахиона может быть только скоростью движущейся системы отсчета. Это прямо указывается подстановкой скорости тахиона в то место уравнений Лоренца, куда ставится скорость системы отсчета, которая по определению содержит часы и оси координат. Других мест в уравнениях Лоренца, куда можно подставить скорость тахиона, просто нет.
Следует отметить, что в среде физиков существуют противоположные мнения о возможности связать с тахионом часы и системы координат. В основном считается, что это сделать невозможно, хотя и встречаются противоположные мнения. Например, на сайте википедии приводится анимационное изображение тахиона:

Рис.10 Изображение тахиона на сайте википедии
Тахион здесь показан как реальный физический объект с явно наблюдаемыми геометрическими формами и размерами: чем не движущаяся тележка из работы Эйнштейна? Это изображение вне всяких сомнений отражает наличие и внутренних координатных осей (размеры тележки) и внутренних часов (изменение положения тахиона в пространстве).
При анализе с этой позиции свойств тахиона фактически используется двойной подход, двойные стандарты: уравнения для энергии и импульса рассматриваются как данность, но уравнения длин и времени обходятся в основном молчанием. Сравним эти уравнения:
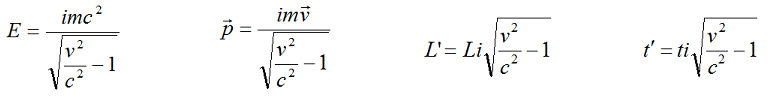
Во всех уравнениях подкоренное выражение сделано действительным путём выделения мнимой единицы. В результате мнимыми следует признать величины m (собственная масса тахиона), L (собственная длина тахиона) и t (собственное время тахиона).
Как обоснование запрета на тахионную систему отсчета можно встретить доводы, что точно также невозможно представить себе систему отсчета, движущуюся со скоростью света, поскольку в такой системе частица (фотон) находилась бы в покое и, следовательно, должны была бы исчезнуть, поскольку масса покоя световых частиц равна нулю. Однако, похоже, те, кто используют этот довод, не замечают, что он содержит гораздо более глубокий смысл, чем видимый на первый взгляд. Достаточно ещё раз вспомнить, из каких условий выводились эти уравнения. Система отсчета в специальной относительности – это система, в которой свет движется с инвариантной скоростью. Не существует в теории относительности систем отсчета, в которых свет не является инвариантом. Придавая системе отсчета скорость, равную скорости света, мы обязаны устранить сразу же возникающее при этом противоречие: свет всё равно в световой системе отсчета должен двигаться со скоростью инварианта. Иначе это особая, не релятивистская система отсчета и она не имеет права на существование в специальной относительности. Система отсчета не может двигаться со скоростью света совсем не потому, что появляется деление на ноль. А потому, что все инерциальные системы равноправны, и во всех них свет должен двигаться со скоростью инварианта. Если это движение не обеспечивается, то такая система не является инерциальной системой отсчета специальной относительности. С таким же успехом можно рассматривать и запрещенную в относительности абсолютную систему отсчета. Именно по этой причине, и ни по какой иной скорость света не может быть придана инерциальной системе отсчета.
Отсюда и возникает важное следствие при сравнительном анализе приведённых выше четырех уравнений. Скорость v во всех этих уравнениях – это скорость инерциальной системы отсчета. Во всех четырех уравнениях – это скорость системы отсчета, которая привязывается к исследуемому движущемуся объекту, в данном случае – тахиону. И в уравнении для энергии, и в уравнении для импульса скорость v – это скорость тахионной системы отсчета, тахиона. Именно для такой одной из равноправных инерциальных систем отсчета были выведены все эти уравнения. Нет никаких разумных доводов в пользу запрета привязки к тахиону системы отсчета. Ссылки на аналогию с фотоном, к которому такую систему привязать нельзя, как показано выше, лишены оснований.
На необходимость привязки к тахиону инерциальной системы отсчета прямо указывают и два других уравнения – для длин и времени. Действительно, что такое «собственная длина тахиона» или «собственное время тахиона»? В пользу их непротиворечивости указывается их неизмеримость, как и неизмеримость массы покоя фотона. Их измерить нельзя, поэтому их мнимость не противоречит физическим законам. И на этом основании опускается вопрос о том «где их нельзя измерить?». Сам тезис о возможности или невозможности измерения подразумевает реальное существование этих величин. Они присутствуют как величины в уравнениях, поэтому у них есть какие-то значения. Измерить их непосредственно мы не можем, но, тем не менее, признаём их существование. Единственное место, где они могут находиться, существовать – это инерциальная система тахиона. Именно в этой системе мы их рассматриваем, не имея возможности физически, непосредственно измерить. Но мы можем вычислить их «в обратном порядке». Ничто не мешает нам определить массу покоя фотона, которую мы не можем измерить непосредственно в его системе отсчета. Точно так же ничто не мешает нам определить собственную мнимую длину тахиона, которую мы тоже не можем измерить непосредственно. Представим себе гипотетический тахионный стержень. У него, как и у тахиона, мнимая собственная длина, мнимое собственное время. Измерив в один и тот же момент времени координаты его концов в нашей системе отсчета, мы измерим длину этого стержня. Зная его скорость, мы можем вычислить его длину в собственной системе покоя. Всё строго по правилам специальной относительности.
Из приведённого выше релятивистского уравнения энергии делается вывод о том, что энергия тахиона падает при увеличении его скорости, а масса его приобретает мнимое значение. Утверждается, то в этом нет серьёзных противоречий, ведь собственная масса тахиона – величина не измеримая, поэтому может быть любой. Но она где-то находится – где? Это собственная масса тахиона, она неотрывна от него, связана с ним, реально существует, как существует тахион, поэтому у неё может быть лишь одно «место» - система отсчета тахиона.
Точно так же мы имеем полное право задать вопрос и о времени: что означает мнимое собственное время тахиона? Если в неподвижной, лабораторной системе отсчета, в которой движется тахион, прошло время t, то для тахиона по уравнениям Лоренца прошло время t’… где? О каком времени в этом случае можно говорить, пусть даже оно и мнимое, если не о времени в системе отсчета тахиона? Если время прошло, одно должно было пройти где-то, по каким-то часам. Иначе вновь следует постулировать, что это мнимое время вообще не течёт. То есть, его не просто нельзя измерить, оно вообще не движется. Конечно, это время, имеющее принципиальное отличие от времени в традиционном и даже релятивистском смысле. Но тогда для него в специальную теорию относительности должен быть введен новый класс систем отсчета, не являющихся релятивистскими.
К чему все эти доводы? У тахиона есть три мнимых собственных параметра – масса, длина, время, приписываемых ему специальной теорией относительности. Следовательно, с тахионным объектом мы в обязательном порядке обязаны связать координатные оси и часы, то есть инерциальную систему отсчета. Эта система должна быть равноправна со всеми другими инерциальными системами. В противном случае мы не имеем никакого права использовать релятивистские уравнения для энергии, импульса, длин и времени.
Но привязка к тахиону релятивистской инерциальной системы отсчета имеет вполне очевидное следствие: если инерциальная система отсчета с часами и координатными осями движется со сверхсветовой скоростью, то скорость света уже не может быть инвариантом. Действительно, если мимо неподвижного наблюдателя движется система со сверхсветовой скоростью, то невозможно создать условия, чтобы движущийся внутри этой системы фотон двигался мимо неподвижного наблюдателя со световой, то есть меньшей скоростью. В общем-то, это должно быть понятно: особенностью инвариантной скорости является её предельность. Любая скорость, выше инвариантной аннулирует её. Сама она при этом может и не быть инвариантом.
Серьёзность проблем, возникающих в специальной теории относительности при введении в неё сверхсветовых скоростей тахионов, вызвала появление компромиссных заявлений о том, что тахион сложно зарегистрировать, что он слабо взаимодействует с веществом или вообще короткоживущий объект. Такими заявлениями как бы устраняются все возникающие при этом акаузальные парадоксы. Однако они устраняют тахион, но не сверхсветовые взаимодействия. Таковые известны в квантовой физике – нелокальные корреляции запутанных частиц. Пока не определено, чем именно обмениваются запутанные частицы при передаче квантовой информации. Но этот обмен происходит явно со сверхсветовой скоростью, о чем свидетельствуют многие эксперименты. В частности, есть данные, что скорость такого обмена на 6-7 порядков превышает скорость света. Повторю, что неважно, как будет названа гипотетическая частица квантовой информации: частица из семейства тахионов, информион, квантино или ньютион. Но уже сейчас неуловимая квантовая информация позволяет показать неприменимость теории относительности к сверхсветовым движениям (например, квантовые «нелокальные кубики»).
При всём при этом, у специальной относительности есть своя бесспорная область применимости. В ней математика теории истинна и не может быть опровергнута никакими мысленными экспериментами. Все акаузальные парадоксы, движение в прошлое при сверхсветовых движениях – это исключительная особенность математики СТО, её преобразований Лоренца. Напротив, в классической физике с её преобразованиями Галилея таких проблем не возникает. Любая теория, опирающаяся на специальную относительность, обязательно получит что-нибудь вроде отрицательного квадрата массы или «машины времени».
Принцип реинтерпретации пытается решить акаузальные проблемы явно не пригодным для этого способом. Проблемы движения в прошлое и «петель времени» решаются путем привлечения не существующих излучателей и приемников, наблюдателей «с провалами в памяти» и введения дополнительной гипотетической частицы - антитахиона. Этот принцип не может использоваться в качестве научного. Его место – рядом со схоластическими дискуссиями о числе ангелов на кончике иглы.
Ложные предсказания СТО для сверхсветовых сигналов
Изложенные выше доводы уже достаточны, чтобы убедиться в невозможности использования математики специальной относительности к сверхсветовым движениям и передаче информации. Возникающие парадоксы делают невозможным последовательное описание таких процессов. В заключение рассмотрим ещё одну проблему, возникающую в специальной относительности при сверхсветовых движениях. Это ложное предсказание теории, то есть два взаимоисключающих предсказания для одной и той же ситуации. Рассмотрим ещё один вариант представленной выше анимации. Пусть в некоторый момент времени подвижная система В оказывается рядом c объектом С, который условно назовём узлом связи «FTL Телеграф Корпорейшн». По каналам связи корпорации наблюдатель В производит сеанс телеграфной связи из точки С с удалённым наблюдателем А в его неподвижной, лабораторной системе. Связь осуществляется тахионными передатчиками, скорость сигналов которых превышает скорость света в 200 раз. Изобразим эту ситуацию на диаграмме Минковского:
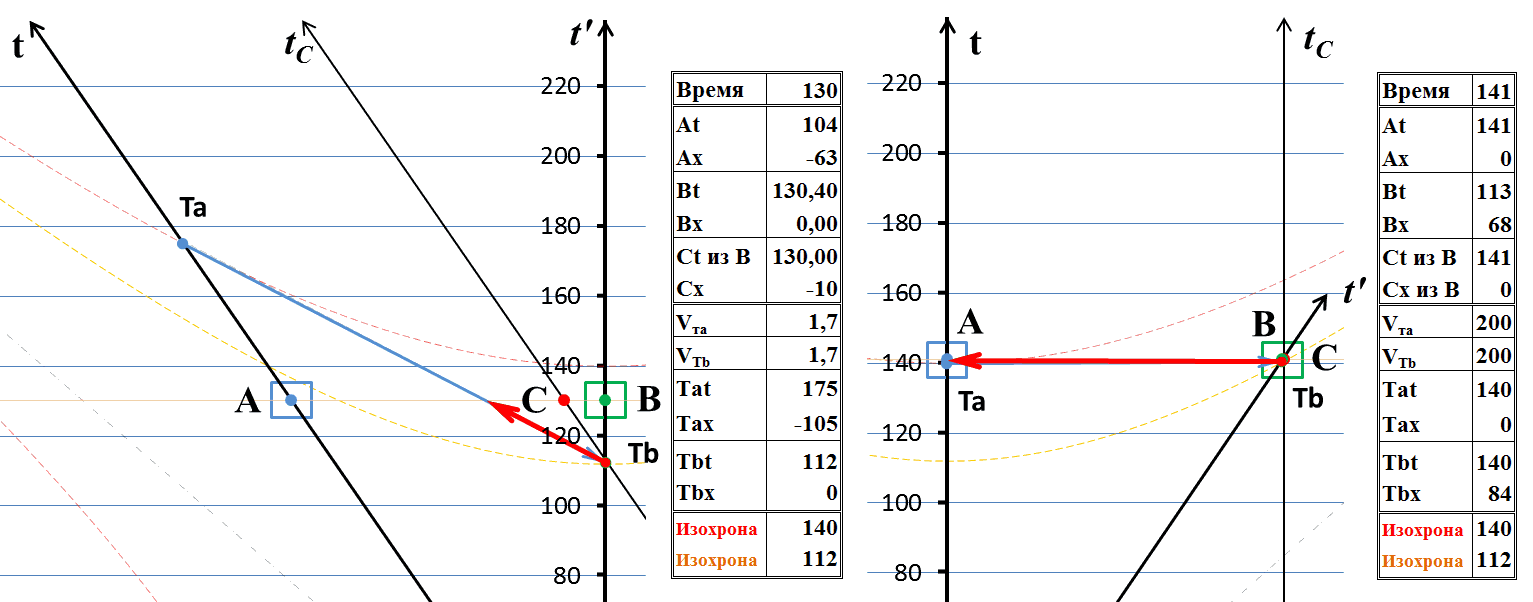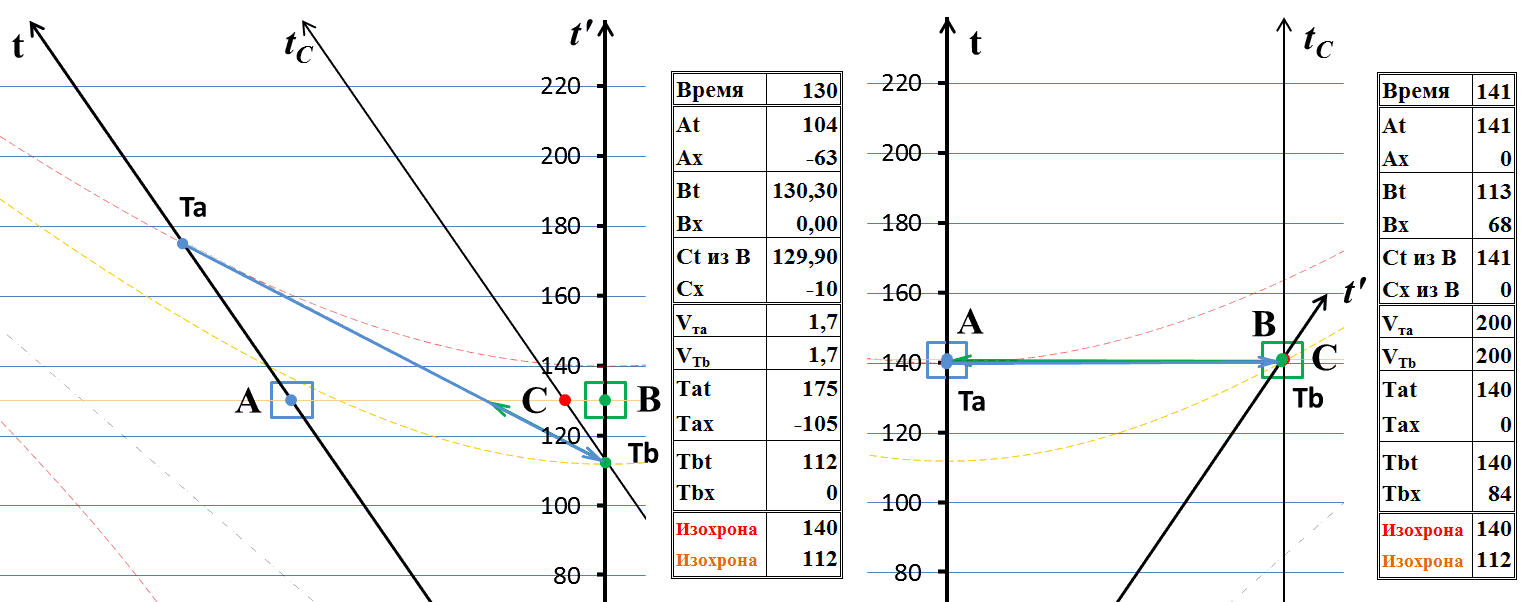
Рис.11 Обмен сигналами по тахионному каналу связи
В полном виде сеанс связи показан на правой стороне рисунка с точки зрения неподвижных наблюдателей А и С. Время будем отмерять в годах. В момент времени 140 лет между тахионными телеграфными узлами связи произведён многократный обмен сигналами, информацией. Как видно на диаграмме, никаких логических противоречий при этом не возникает. Время по часам А и С – это какой-либо день по истечению 140 лет движения системы В. Очевидно, что за это время он удалился от А на расстояние 84 световых года. Вследствие релятивистского замедления темпа хода часов в системе В календарь и часы показывают время в какой-то день 113-го года (если отсчет дат велся с нуля). Хотя это и выглядит как передача сигнала «в прошлое», но это прошлое получателя, а не отправителя и никаких противоречий в этом нет.
Теперь посмотрим на диаграмму на левой стороне рисунка. Там мы видим, что с точки зрения наблюдателя В никакого обмена сигналов пока ещё не было. Входное сообщение от наблюдателя А он вроде бы получил, хотя довольно странным способом: из будущего. Но его ответный сигнал до наблюдателя А ещё не дошёл. Соответственно, как такового не было не только обмена сообщениями, но пока не было даже и однократного ответа. Выше на примере обмена световыми сигналами мы рассматривали схожую ситуацию и пришли к выводу, что в том случае никакого противоречия нет, поскольку время для получения ответного сигнала у получателя ещё не наступило. А что мы видим здесь? Здесь ситуация совершенно иная. По часам наблюдателя А, как и при световом обмене, время получения ответа ещё не настало, это нормальная ситуация. Но вот по часам наблюдателя В мы видим невозможное: с точки зрения В на левой диаграмме в более поздний момент времени обмена не было, а с его же точки зрения, в более ранний момент, на правой диаграмме – был. Действительно, календарь и часы В на правой диаграмме показывают время в какой-то день 113-ого года. А на левой диаграмме – некоторый день в 130-ом году. Это более поздняя дата, поэтому сеанс связи уже должен был состояться и стать достоянием истории. Но этого на диаграмме нет: с точки зрения наблюдателя В сигнал ещё только движется к А и прибудет туда никак не раньше 170-го года. Обмена сигналами не было. При обмене световыми сигналами, как мы выше видели, время прибытия ответного сигнала не зависело от того, кто наблюдает за обменом и из какой системы отсчета. Здесь же принцип относительности, безусловно, нарушен: результат зависит от того, из какой системы отсчета мы наблюдаем за процессом.
Таким образом, сверхсветовой канал связи вынуждает специальную теории относительности делать взаимоисключающие предсказания для одной и той же ситуации. Теория, которая даёт такие противоречивые предсказания, являет ложной теорией. В данном случае ложной является расширенная сверхсветовыми движениями специальная теория относительности.
Список произведений >>
Список публикаций >>
Оценить статью можно после того, как в обсуждении будет хотя бы одно сообщение.
Тест: А не зомбируют ли меня? Тест: Определение веса ненаучности
Создан синаптический коммутатор с автономной памятью и низким потреблением
Ученые Северо-Западного университета, Бостонского колледжа и Массачусетского технологического института создали новый синаптический транзистор, который имитирует работу синапсов в человеческом мозге.
Тематическая статья: Как образумить Beast?
Рецензия: Статья П.К.Анохина ФИЛОСОФСКИЙ СМЫСЛ ПРОБЛЕМЫ ЕСТЕСТВЕННОГО И ИСКУССТВЕННОГО ИНТЕЛЛЕКТА