Абстракция и математическая интуиция Жан Дьедонне

Жан Дьедонне[1]

Источник: Математики о математике, М.:«Знание». 1982; оригинал: Par Jean Dieudonne. L' abstraction et l'intuition matliematique. Tire a part de «Dialectica», Revue internationale de philosophie de la connaissance Vol. 29 №1 [1975] Case postale 1081, 2501 Bienne [Suisse]

Все математики единодушно признают основополагающую роль, которую воображение играет в математическом творчестве. Логика — это необходимый и скучный инструмент (известно, что математики ее, вообще говоря, не слишком ценят); ею надо уметь должным образом владеть, так как она позволяет следить за доказательством и проверять его... но не изобретать!

Но как же изобретается доказательство? Этот процесс прекрасно описал А. Пуанкаре на ставших знаменитыми страницах: воображение предоставляет математику, стоящему перед лицом некоторой проблемы, множество всевозможных комбинаций известных фактов, теорем, однако большинство из них никуда не ведет. Если случайно математик нашел верный путь, то говорят, что у него хорошая интуиция, которая его удачно направляла. Но как только речь заходит об интуиции, сейчас же возникает недоразумение, проистекающее из того, что это слово уже имеет одно значение — кстати, очень расплывчатое — в разговорной речи, касающейся вполне обыденных вещей и явлений, и это приводит нас прямо в центр проблемы, затронутой на этом коллоквиуме.

Никто, конечно, не думает отрицать, что источником основных математических понятий, таких, как число или пространство, является чувственный опыт. Начиная примерно с 12 лет, если верить профессиональным психологам, небольшие натуральные числа или простые пространственные отношения (положение, величина и т. д.) могут рассматриваться как устойчивые, базирующиеся на опыте понятия, присущие всем нормальным людям и образующие субстрат соответствующих математических понятий. Однако необходимо сразу же отметить одно обстоятельство, которое, на мой взгляд, недостаточно учитывается: математические объекты, претендующие на выражение этих опытных понятий, наделяются математиками такими свойствами, которые явно выходят за пределы опыта. Возьмем, например, произвольное натуральное число: я сомневаюсь, что кто-либо обладает серьезной интуицией натурального числа, большего, чем 10 (я имею в виду непосредственное восприятие; насколько мне известно, существуют психологические опыты, в которых требуется, не считая, определить количество возникающих на экране точек, и при этом безошибочный ответ дается лишь тогда, когда число точек не превосходит 7). Понятия неограниченно продолжаемого натурального ряда чисел, бесконечной прямой и т. д. могут служить примерами концепций, не имеющих непосредственного экспериментального обоснования. Существование точной верхней грани, аксиома о вложенных отрезках, говорящая о том, что при неограниченном разбиении отрезков существует общая точка для всех полученных отрезков - все это, строго говоря, нельзя проверить экспериментально. То же замечание относится и к постулату Евклида.

После двухвекового раздумья над этими вопросами мы теперь знаем, что выбор аксиом производится математиками довольно произвольно иногда из эстетических соображений или, по Пуанкаре, из соображений удобства; они вовсе не навязываются извне некоторыми явлениями или чувственной интуицией, которую мы можем иметь по отношению к ним. Кстати, история показывает, что некоторые аспекты этой чувственной интуиции могут вступать в столкновение, когда встает вопрос о выборе между ними. Г. Гирш напоминал в своем выступлении, что пифагорейцы были приведены к рассмотрению не действительной прямой в нашем обычном понимании, а «рациональной» прямой. Почему так произошло? Из-за меры: имеются две длины, и вполне естественно считать, что у них есть общая мера. Это совершенно логично, однако произошло столкновение с другой стороной интуиции: когда захотели измерять отрезки, возникающие в геометрии на плоскости, обнаружили, что существуют длины (например, диагональ единичного квадрата), которые не отвечают этому требованию. И тогда необходимо было выбрать: заниматься ли геометрией на плоскости, в которой диагональ квадрата имеет длину, или считать, что диагональ квадрата длины не имеет. (Кстати, это вполне можно было бы допустить. Геометрия над полем рациональных чисел совершенно разумна, но только некоторые утверждения в этой геометрии становятся ложными.)

Другими словами, имеются причины, связанные с историческим развитием математики, по которым на понятия, возникшие в основном из опыта, стали налагать требования, которые вовсе не имеют такого происхождения, и которые выступают в качестве аксиом, наложенных на понятия, выбранные в качестве основных. После этого, естественно, нет ничего удивительного, хотя это и смущало людей в свое время, что чувственная интуиция рассматриваемых объектов, хотя бы действительных чисел, либо в некоторых случаях совершенно не существовала, либо была недостаточной и обманчивой. Она не существовала в упомянутом выше случае произвольно больших натуральных чисел: если бы имелась мгновенная интуиция произвольно больших натуральных чисел, получение результатов теории чисел не представляло бы труда, в то время как на самом деле это весьма сложное дело и к результатам этой теории приходят путем огромных усилий, использующих всевозможные ресурсы, лежащие вне ее. Никто не может сказать, что у него есть интуиция истинности или ложности теоремы Ферма. Иногда интуиция, которой обладают относительно некоторых понятий, начиная с аксиом, дает идею доказательства. Классическим примером может служить теорема Больцано, говорящая о том, что непрерывная функция не может изменить знак, не обратившись в нуль. Здесь есть достаточно четкая геометрическая интуиция, которая дает идею доказательства. Если же попытаться доказать теорему Жордана*, которая тоже интуитивно очевидна, выясняется, что здесь интуиция обманчива. Имеются и вовсе неинтуитивные объекты, классические чудовища: кривая Пеано, континуум Брауэра, который является общей границей трех плоских областей, кольцо Антуана, являющееся вполне разрывным множеством, хотя существует кривая, которую нельзя деформировать в точку, не пересекая этого кольца. Кстати, чтобы не заходить в столь далекие области, можно привести такие примеры ложной интуиции, как знаменитый чертеж, с помощью которого доказывают, что всякий треугольник равнобедренный. Если сделать чертеж так, что точка пересечения перпендикуляра к середине стороны и биссектрисы противолежащего угла окажется внутри треугольника (что, очевидно, невозможно), легко показать, что треугольник равнобедренный. Этот пример хорошо иллюстрирует тот факт, что пространственная интуиция, вырабатываемая в нас элементарной геометрией, может оказаться обманчивой.

Поэтому не надо давать себя обманывать. Даже для понятий, которые кажутся близкими к чувственной интуиции, соответствующие математические объекты, в сущности, очень отличаются от того, что мы о них думаем. В этом факте кроется источник огромного удивления, возникшего у большинства математиков XIX века, полагавших, что понятия, которые они ассоциировали с действительными числами, сами собой разумеются и не могут привести к экстравагантным результатам, подобным кривой Пеано.

Мы больше не удивляемся таким явлениям. Начиняя с конца XVI - XVII века математики разрушили классическое представление о числе и пространстве и начали исследовать объекты, не имеющие никакого чувственного эквивалента. Никто никогда не видел группы, кольца, тела, модуля. Геометрии Лобачевского, Римана и все другие геометрии, р-адические числа*, дифференцируемые многообразия созданы математиками. Как же можно говорить об интуиции для этих объектов? Ответ на этот вопрос, безусловно, трудно сформулировать, так как речь идет о явлениях совершенно субъективных. Каждый математик создает себе индивидуальный мысленный образ, в чем-то несравнимый с соответствующими образами мыслей других. Поэтому анализ, который я попытаюсь провести, прочно связан с моими собственными образами. Иначе не могло бы и быть, и я, не претендуя на произнесение всеобщих истин, просто попытаюсь прояснить некоторые умственные процессы, которые мне все же кажутся примерно общими для многих математиков.

Вначале отметим распространенную и совершенно банальную точку зрения: интуиция математического объекта постепенно развивается и зависит прежде всего от степени знакомства с этим объектом. Что делает математик, когда перед ним встает совершенно новая для него проблема, которую он никогда не изучал и над которой он только начинает работать? Чаще всего он либо совсем не знает, какие вопросы надо ставить, либо ставит абсурдные вопросы. Здесь типичным примером может служить А. Пуанкаре (к счастью, Пуанкаре, будучи самым большим математиком своего времени, счел нужным очень точно описать свои впечатления об исследованиях). Когда Пуанкаре начал работать над автоморфными функциями, как он сам говорит об этом в своей книге, он пытался доказать, что не существует других автоморфных функций, кроме тех, которые были хорошо известны в то время (в том числе модулярных функций). Отсюда видно, до какой степени даже самые крупные математики могут двигаться в совершенно абсурдном направлении. Пуанкаре заметил это сам, и именно в этом проявилась его, как говорят, большая интуиция, потому что, изучая вопрос, понемногу начинают осваиваться в незнакомой стране; привыкая, приходят к умению угадывать, что должно произойти, когда встречают данный математический объект, и какой инструмент нужно применить для его исследования. Постепенно прекращаются нелепые ошибки, допускаемые вначале. В конце концов вырабатывается определенная привычка к теме и, если повезет, удается поставить проблему и решить ее.

Это очевидно, и все-таки банально говорить, что интуиция просто является плодом хорошего знания темы. Я верю, что есть крайние случаи, где, нет ничего другого, кроме хорошего знания, ибо речь идет об объектах совершенно абстрактных, не имеющих никаких связей с другими математическими понятиями. Для меня типичным примером (здесь большую роль играет личное восприятие) является область, в которой я никогда не работал — теория конечных групп. Конечная группа — это объект, который нельзя увидеть, здесь нет никакого рода интуиции. Люди, работающие в этой области, приобретают такое знакомство с предметом, что у них, по-видимому, возникает чутье к абстрактным понятиям теории групп. Я откровенно признаю, что ни силовская подгруппа, ни таблица характеров ни о чем мне не говорят, в то время как специалисты имеют свое образное чутье и привычку к этим понятиям, позволяющие им распутывать сложные узлы и получать результаты. То же самое можно сказать по поводу почти всей абстрактной алгебры и многих проблем комбинаторного характера. Среди последних, очевидно, есть случаи, где имеется некоторое видение вещей (графы, например) — их можно точно представить графически, геометрически. Но есть и другие, где интуиция порождается лишь хорошим знанием вопроса.

Идя дальше, можно рассмотреть вопросы комбинаторного типа, связанные с анализом. Например, что могло натолкнуть Эйлера на мысль о том, что для изучения последовательности целых чисел, заданной некоторым арифметическим процессом, полезно рассмотреть ряд Тейлора с коэффициентами, равными членам этой последовательности? Я думаю, что Эйлеру первому пришла мысль о производящей функции. Можно, конечно, сказать, что это одна из форм гармонического анализа, но это лишь переносит вопрос в другую область. В идее, что поведение ряда отражается некоторым образом на функции и обратно, заключается нечто вроде чуда — необыкновенная интуиция, источник которой, на мой взгляд, необъясним. Некоторые математики, однако, обладают, можно так сказать, комбинаторной интуицией: те, которые занимаются теорией групп, делают видимой чистую комбинаторику. Это происходит, вероятно, благодаря знанию вопроса и особенно, может быть, благодаря изучению частных случаев. Я был учеником Попа, который дружил и сотрудничал с Харди. Первый мне всегда говорил, что Харди советовал своим ученикам, желавшим доказать теорему, зависящую от параметра и, сначала провести доказательство для n=1, а потом для n=2, n=3. К этому моменту они, быть может, начинали понимать, что происходит, и у них могла появиться идея доказательства в общем случае. Этот метод не всегда выручает, но иногда он оказывается полезен.

Вот то, что касается интуиции, которую я бы назвал  комбинаторной; это крайний и, думаю, не самый интересный случай. Остальную часть доклада я посвящу другому типу математической интуиции, а именно тому, что я бы назвал переносом интуиции. Этот тип интуиции я считаю основным и являющимся одним из наиболее важных источников математического развития. Сейчас я приведу примеры, которые позволят мне более ясно выразить свою мысль. Есть несколько видов такого переноса, и я начну говорить о наиболее простых. Существуют, во-первых, переносы, которые можно назвать тривиальными; классическим примером может служить в геометрии переход от пространства R² к R^n*. Имеется большое число результатов, которые можно доказать для плоскости, причем это доказательство настолько механично, что нетрудно заметить возможность его проведения таким же образом и для Rⁿ. Переносят доказательство и одновременно переносят интуицию. Таким вот образом в XIX веке постепенно поняли, что в исчислении с переменными разумно использовать не алгебраический, а геометрический язык. Вместо того чтобы говорить об уравнении а₁х₁+ а₂x₂+...+ а_пx_n=b, говорят о гиперплоскости, задаваемой этим уравнением; строго говоря, с точки зрения математики ничего нового не добавлено, а введено понятие, напоминающее уже известное для случая n = 2 или n = 3, о котором мы имеем геометрическую интуицию. Таким образом, происходит перенос от случая тривиального, элементарного, интуитивного в самом обычном смысле, к случаю, где больше нет чувственной интуиции, но где существует эта перенесенная математическая интуиция.

Рассмотрим несколько более сложный пример, не сводящийся к простым выкладкам: доказательство того, что в пространстве Rⁿ всякое ортогональное преобразование и есть произведение симметрии. Хорошо известно доказательство этого факта для случая R².

Рассмотрим точку а! = 0. .Найдется симметрия s, такая, что s (a) =u (а) (в качестве оси симметрии следует взять перпендикуляр к отрезку с концами а и и (а) в середине этого отрезка). Но тогда su (а) =а, поэтому ортогональное преобразование su оставляет точку а неподвижной и, следовательно, является либо тождественным преобразованием, либо симметрией относительно прямой Оа.

Для Rⁿ рассуждают так же: su переводит в себя гиперплоскость Н, перпендикулярную к Оа, но su, рассматриваемое лишь на Н, можно разложить в произведение симметрии (индукция по п).

Я бы назвал этот перенос тривиальным. Есть и другие, тоже очень интересные, хотя и менее простые примеры. Предположим, что хотят доказать, что группа вращений является простой над своим центром для n >= 5. Здесь есть небольшое осложнение, так как это верно для п=3, для n>=5 и неверно для n = 4. Его устанавливают для n = 3, затем с помощью некоторых искусственных приемов перепрыгивают через случай n = 4 и продолжают доказательство для п >= 5. Перенос интуиции, несколько менее тривиальный, возникает, когда вместо перехода от пространства R² к Rⁿ переходят от Rⁿ к Кⁿ, где К — более или менее произвольное поле. При этом возникают определенные трудности, но если сделать о К некоторые разумные гипотезы, то большая часть геометрии переносится на геометрию над почти произвольным полем. Можно пойти значительно дальше. Часть этих свойств остается верной и при замене поля на кольцо*. Не в обиду Тому, вся линейная или полилинейная алгебра оказывается, таким образом, добавлением к геометрии, в то время как геометрия не является добавлением к линейной или полилинейной алгебре. Для меня это различие не имеет никакого значения; есть теория, которая одновременно является линейной или полилинейной алгеброй и геометрией. Их разъединяет лишь язык, но он же и оказывает огромную помощь, так как позволяет в каждый момент более или менее точно подыскать сходные интуитивно знакомые ситуации и перенести интуицию из этих ситуаций на случаи более сложные. Это не очевидно и надо часто принимать серьезные предосторожности; но это помощь, которую я лично очень люблю и нахожу настолько важной, что обучение ей мне кажется существеннейшим делом.

Рассмотрим другой тип интуиции, который менее прост. Важнейшим моментом в истории анализа явился переход от конечного к бесконечному. Он берет начало еще в XVIII веке, когда Даниил Бернулли пытался вывести уравнение колеблющейся струны. У него возникла идея заменить струну из нити заданной плотности конечным числом материальных точек, расположенных на невесомой нити, и изучить колебания этой системы; затем он перешел к пределу, устремив число точек к бесконечности и сделав, таким образом, струну однородной, откуда и получил уравнение колеблющейся струны. Фурье поступал аналогичным образом в большом числе других случаев. Этот метод оставался более или менее в тени в течение всего XIX века и вышел на авансцену лишь в конце его в известных работах Вольтерра и Фредгольма об интегральных уравнениях. Их основная идея состоит в рассмотрении интегрального уравнения как предела системы линейных уравнений. В уравнении

f (x) =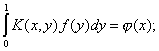         

придают х значения k/n (0 <= k <=n) и заменяют интеграл «римановои суммой» —

 . Полагая =t_k, =b_k, a_kh,

получают таким образом систему n линейных уравнений относительно t_k

t_k+  (a_kht_h)  = b_k (0<=k<=n-1)

решаемую с помощью формул Крамера. Затем устремляют n к (+) и получают формулы Фредгольма.

Несколько позже таким же образом и поступил Гильберт при изучении квадратичных форм. Он исходил из теории квадратичных форм с n переменными и, переходя к пределу, вывел из нее теорию пространств, названных гильбертовыми, и теорию вполне непрерывных симметрических операторов. Идея заключается в том, чтобы в конечном рассмотреть алгебраическое понятие суммы и перейти от конечного к бесконечному двумя способами; конечная сумма становится рядом или интегралом. Так алгебраический процесс приводит к двум процессам математического анализа. Конечные суммы, линейные комбинации принадлежат в основном области классической линейной алгебры, т. е. теории конечномерных пространств; переходя к бесконечности, приходят к функциональным пространствам. От конечной суммы квадратов переходят к интегралу Лебега** от квадрата функции, что уже вовсе не тривиально. В это гильбертово бесконечномерное пространство переносят всю евклидову геометрию, принимая, конечно, меры предосторожности. Удивительно, насколько большая часть информации и результатов евклидовой геометрии без малейшего труда переписывается для гильбертова пространства с произвольным числом измерений. Затем, естественно, пошли много дальше и перешли к более сложным пространствам, таким, как банаховы и локально выпуклые пространства. Я повторяю, что, безусловно, необходимо принимать некоторые предосторожности при таких переносах. В действительности в начале века математики дали себя увести своей интуиции слишком далеко. Были трудности, которые мы теперь хорошо понимаем, трудности топологического характера, которых не могли увидеть в свое время, например, Пинчерле в Италии, П. Леви и Гато во Франции. Другими словами, необходимо было в некотором смысле приручить эту интуицию, перенесенную из конечного в бесконечное; ее нельзя было оставить без изменений, а надо было научиться с нею соответственным образом обращаться. Так возникла общая топология, которая, выявив небольшое число простых понятий, позволила увидеть, что дозволено и что стало недозволенно. Случай меры был значительно более сложным, и потребовалось долго ждать, пока возникли понятия, подходящие для достаточно общих пространств. Вот, следовательно, второй пример переноса интуиции, который все еще следует в направлении, указанном математической интуицией.

Иначе обстоит дело с третьим типом, к которому я теперь подошел: алгебраическая топология и дифференциальная топология в пространствах размерности выше трех. Алгебраическая топология была создана Риманом, но он работал с размерностью 2 (за исключением фрагмента в одном из его писем, где, однако, способ рассуждения не до конца понятен). Рассуждения, содержащиеся в его работах, целиком основаны на пространственной интуиции, относящейся к двухмерному многообразию, хотя речь идет не об обычном пространстве. Рассматривается не плоскость, а риманова поверхность, более или менее расстеленная на плоскости. Рассуждения носят явно интуитивный характер и не могут считаться доказательными в настоящее время. Этот процесс, который не мог быть сохранен, особенно при переходе к высшим размерностям, был преобразован Пуанкаре и Брауэром в комбинаторные рассуждения. Чрезвычайно удобной оказалась идея, не содержавшая, впрочем, слишком большого новшества и заключающаяся во «впрыскивании» в эту теорию алгебры: Эмми Нетер рассмотрела группы, составленные из произвольных комбинаций симплексов определила с помощью понятия границы симплекса граничные гомоморфизмы* этих групп и из них вывела группы гомологии Пуанкаре средствами чисто линейной алгебры (в основном рассматривая факторизацию ядра по образу).

Это вмешательство Эмми Нетер было переносом алгебраической интуиции, полученной в результате владения линейной алгеброй, на вопросы топологии; удивительно, что это получилось и получилось хорошо. Достаточно перечислить имена математиков, введших алгебру в алгебраическую топологию: Гуревич, X. Хопф, Уитни, Стинрод, Эресман, А. Картан, Лерэ, Том, Милнор, Гротендик, Салливан, Уолл, Кирби, Зиберманн и т. д. В их работах проводится в жизнь та же идея — в этом мне не будет возражать Том, введший новый способ произвольно комбинировать объекты в модулях и составлять таким образом новые группы, оказавшиеся очень полезными в развитии теории. Последней появилась и оказалась наиболее удивительной К-теория, введенная прежде всего Гротендиком. Я не буду пытаться ее описывать, так как это было бы слишком сложно, отмечу лишь, что теперь она простирается над всей математикой. В действительности здесь имеет место слияние двух типов интуиции. Есть интуиция, исходящая из области линейной алгебры, и, кроме того, без всякого сомнения, геометрическая интуиция; люди, которые успешно изучают эти вопросы, как говорится, «видят» в пространстве, причем не только в обычном пространстве, но и в пространстве произвольной размерности. Это замечательное, но, думаю, не очень распространенное свойство. Несколько позже я буду говорить об обратном воздействии топологии на алгебру, осуществляемом часто теми же людьми.

Вот три типа примеров, которые являются неочевидными переносами, но в некотором смысле более или менее естественными. В подобных случаях есть нечто, толкающее нас переносить идеи на другую математическую теорию. Но, так сказать, встречаются великие переносы, которые можно было бы назвать мутациями и которые — иначе не скажешь — падают с неба. О них создается впечатление, что они совершенно ничем не подготовлены. Далее я буду говорить о триединстве, состоящем из теории алгебраических многообразий, теории аналитических многообразий, являющейся старинной теорией комплексных функций с несколькими переменными, и наконец, теории чисел. Начиная с Римана, три теории взаимодействуют друг с другом необычайным образом. Риман исходил из математического анализа и применил его к алгебраической геометрии; при этом произошло создание бирациональной геометрии. Он начал не с геометрических идей, а с теории абелевых* интегралов, входящих в математический анализ. Для того чтобы уметь описывать эти функции, он изобрел сразу двухмерную алгебраическую топологию и поверхности, названные римановыми; в качестве, так сказать, побочного продукта он получил фундаментальные понятия теории алгебраических кривых, в частности, например, род. Итак, исходя из математического анализа, Риман создает новую теорию, называемую бирациональной алгебраической геометрией кривых. Две изоморфные римановы поверхности соответствуют двум изоморфным алгебраическим кривым. Но, более того, Риман, обладая таким инструментом, как учение о мероморфных** функциях на римановой поверхности, заметил, что эти функции образуют поле и что изучение одной алгебраической кривой является, главным образом, изучением поля рациональных функций. Он пришел к понятию чистой алгебры — полю рациональных функций кривой, которое является попросту конечным расширением поля рациональных дробей над комплексными числами. Одна из теорем Римана устанавливает, что две римановы поверхности бирационально*** эквивалентны тогда и только тогда, когда соответствующие поля изоморфны. Но тут же вслед за Риманом Дедекинд и Вебер изменили ситуацию и приняли поле в качестве отправной точки. В это время Дедекинд закончил изучение совершенно аналогичной проблемы, а именно теории алгебраических кривых, где поле С (х) рациональных функций было заменено полем рациональных чисел. Для этого он ввел новые методы, полученные под влиянием работ Куммера, но совершенно от них отличные, — методы линейной алгебры для идеалов. Он построил всю теорию этих полей, исходя, главным образом, из теории алгебраических чисел. Он заметил, что ситуация похожа на риманову в том смысле, что имеет дело с конечным расширением поля С (х), и у него возникла идея применить к теории алгебраических кривых методы, которые он удачно использовал в теории чисел. Кстати, несложно установить взаимосвязь между этими двумя понятиями: алгебраическая кривая соответствует полю рациональных дробей; точки кривой примерно соответствуют простым идеалам**** поля К, рассматриваемого как конечное расширение поля С (х). Итак, в случае алгебраических полей простые идеалы лежали в самом основании теории Дедекинда. Мы имеем здесь перенос интуиции алгебраических теорий: простой идеал становится точкой, чисто алгебраическое понятие преобразуется в геометрическое, даже, если угодно, топологическое. Мы получаем, таким образом, две первые стрелки:

Аналитические многообразия  --->  Алгебраические многообразия

                                                                                ↑

                                                                                ↑

     Алгебраические  числа

Далее это триединство продолжает развиваться еще более неожиданным образом. Во-первых, появляются р-адическне числа, созданные Гензелем:

Аналитические         <---               Алгебраические

многообразия                    многообразия

         ↑

         ↑________________________

                                                                                     ↑

                                                                                     ↑

Гармонический           --->     Алгебраические

                      анализ                                  числа

В этом случае алгебраическая кривая является просто полем комплексных чисел. Для данного многочлена Р над комплексными числами можно записать в окрестности точки х₀:

1/P(x)=1/{(x-x₀)^k P₁(x)},   P₁(x₀)! = 0, k >= 0 - целы.

Следовательно, каждая рациональная дробь может быть записана в аналогичном виде:

R (х) = R₁(х)(x-x₀)^h (h > 0 или h < 0 или h = 0; R₁(x₀)  != 0)

Таким образом, каждой точке плоскости и каждой рациональной дроби приписывается порядок. Но так как рассматривается комплексная плоскость, можно пойти значительно дальше. В распоряжении имеется теория аналитических функции; следовательно (так как R₁(x₀) != 0, R₁ — голоморфно в окрестности x₀) R₁ можно разложить в степенной ряд. Рациональная дробь, т. е. элемент поля, являясь аналитической функцией, имеет в окрестности точки разложение в сходящийся ряд. Но имеются также разложения в ряд, не являющиеся рациональными функциями. Замечательная идея Гензеля заключается в том, что так же обстоит дело и в числовых полях. Другими словами, совершается обратное тому, что было сделано только что; исходя из известных свойств алгебраических кривых, получают нечто новое для теории чисел. Гензель, не колеблясь, продолжает приведенную выше аналогию между идеалом и точкой. Рассмотрим более простой случаи — поле комплексных чисел и возьмем в качестве основного поля совокупность рациональных  чисел. В теории чисел точке соответствует простой идеал, а в случае рациональных чисел это в точности простое число р. Тогда Гензель изучает (1—р)^-1 и говорит себе, что он должен иметь право представить это в виде 1 + p + p² + ... + pⁿ +  ..., что рассматривалось в свое время как чрезвычайно смелая мысль; тем не менее она была вполне обоснована для, тех, кто мыслил арифметически. Сказать, что два числа равны, значит сказать, что их разность равна 0. В то же время с точки зрения делимости на р можно считать два числа близкими, если их разность делится на большую степень р, потому что если она делится на произвольную степень р, то она обязательно равна 0: это теорема о разложении целого числа на простые множители. Учитывая это, идея Гензеля становится намного более естественной; она попросту означает, что если остановить разложение на некотором шаге, то разность

1/(1-p) - (1 + p + p² + ... + pⁿ)

делится на рⁿ—1 Это грубая манера представлять вещи, но она позволяет понять аналогию между разложением Тейлора рациональных функций и этим видом асимптотического разложения — в арифметическом смысле — рационального числа по степеням р. Гензель с успехом развил эту идею, и стало возможно говорить об анализе в окрестности простого числа. Идея заключается в том, что элементы поля, т. е. рациональные числа, соответствуют рациональным, дробям из аналитического случая или алгебраического случая и что, так же как и рациональная дробь в окрестности точки, они допускают разложение Тейлора (рациональное число имеет р-адическое разложение). Кроме того, имеются р-адические числа, не являющиеся рациональными. Эти наблюдения распространяются на поля алгебраических чисел и значительно дальше на множество аналогичных случаев; в настоящий момент таким способом излагают теорию Дедекинда — Кронекера. Разложение на простые идеалы, являющиеся основной теоремой теории алгебраических чисел, наиболее естественным образом выражается как теория р-адических нормировании. Таким образом, имеется в распоряжении в некотором роде локальная теория аналитических функции, которая преобразовывается в локальную теорию чисел. На этом дело не заканчивайся, так как теория аналитических функции не только локальная, но  общая теория. Зная аналитическую функцию, мы знаем не только разложение в окрестности одной точки, но и в окрестности всех точек. Возникает, таким образом, проблема обобщения; эта проблема не была поставлена во всех деталях самим Гензелем. а развивалась лишь после работ Шевалье и его последователей в 40-х годах.

Шевалье связал эту теорию с топологическими абелевыми группами. Но еще в это же время было замечено, что теория Фурье, классический гармонический анализ, развитый для случая действительных чисел или тора, можно почти без изменений переписать для случая локально компактных абелевых групп. Это повлекло за собой новый перенос интуиции (гармонический анализ обогатил теорию чисел) и позволило «на серебряном подносе» получить все теоремы теории алгебраических функций как частные случаи теорем о локально компактных абелевых группах: теорему о разложении простых идеалов, теорему Дирихле о единицах, теорему об ограниченности классов идеалов и даже всю теорию полей классов. Лучшим способом развития теории полей классов, вершины теории алгебраических чисел, является в наши дни использование гармонического анализа — метода, подробнейшим образом разработанного в книге Андре Вейля «Основы теории чисел» [русский перевод этой книги вышел в 1972 году в издательстве «Мир»]. Можно сказать, что теория алгебраических чисел стала одной из глав коммутативного гармонического анализа. Но я должен пойти значительно дальше и сказать, что к теории чисел применяется не только коммутативный гармонический анализ, но также и некоммутативный гармонический анализ. Я должен сказать еще несколько слов об особенно замечательном обратном воздействии переноса интуиции. Я только что показал, каким образом интуиция линейной алгебры была перенесена на алгебраическую топологию и привела к значительному прогрессу. Самое же замечательное заключается в возвращении этого влияния назад. Математики, работающие над алгебраической топологией, пришли к развитию целой серии специальных или на первый взгляд специальных для их объектов исследования методов. Речь шла о вопросах строго топологических до тех пор, пока. в один прекрасный день алгебраисты Эйленберг и Мак Лени в 1942 году, Хопф и А. Картаи примерно в то же время заметили, что в вопросах чистой алгебры встречаются аналогичные ситуации, и им пришла в голову мысль перенести на задачи чистой алгебры методы, успешно применяемые алгебраическими топологами; успех был совершенно необычайный: гомологическая алгебра явилась рикошетом интуиции чистых алгебраических топологов. Она получила разнообразные применения в коммутативной алгебре, локальной алгебре, теории чисел, теории дискретных групп и т. д.

В заключение я хотел бы отметить, что приведенные примеры, несмотря ни на что, наиболее простые. Чтобы описать современное бурное кипение идей, надо было бы говорить о больших конструкциях, где сливаются не одна-две, а полдюжины интуиции. Упоминавшаяся выше K-теория является тому типичным примером. Она простирается от теории чисел к уравнениям в частных производных и охватывает алгебраическую топологию, дифференциальную топологию, теорию линейных групп и т. д. Она проходит через всю математику, и в ней смешиваются почти все интуиции: современная алгебраическая топология, схемы, топологии Гротендика, приложения к алгебраической геометрии и т. д. Этот факт свидетельствует, во-первых, о жизненности этой теории, а также о том, насколько гибким и изобретательным может быть человеческий разум в построении необычайно разнообразных и плодотворных интуиции.

Первый вывод, который я делаю из вышесказанного, состоит в том, что в математике, безусловно, нет одной интуиции; в ней есть целая серия разнообразных установок, порою неожиданно между собою взаимодействующих. Второй вывод: математические интуиции не постоянны; они непрерывно пополняются новыми вкладами в науку, новыми результатами, новыми идеями. Почти каждый год появляется незаурядный молодой математик, показывающий новый способ перенесения интуиции из одной области в область, совершенно от нее отличную. Наконец, в-третьих, возвращаясь к теме доклада: прогресс интуиции вопреки тому, что можно было бы предположить, идет рука об руку с прогрессом абстракции. Чем более абстрактно явление, тем больше оно обогащает интуицию. Почему? Потому что абстракция устраняет из теории все несущественное. Если вы вводите абстракцию умело и ведомы своим чутьем (интуицией, если угодно), то вы отбрасываете несущественные отношения. Что же осталось? Остался скелет, и в этом скелете вам иногда удается обнаружить структуры, которые иначе вам увидеть бы не удалось. Если бы вы не ввели абстракцию, деревья заслонили бы от вас лес, детали помешали бы вам увидеть существенное. Итак, я думаю, что все сказанное мною должно служить примером тому, что прогресс математической интуиции, которую я попытался определить, всегда сопутствует прогрессу математической абстракции. Возможно, это мучительно для лиц, желающих ее постичь, но я не думаю, что кто-то сможет этого избежать. В этом, мне кажется, и заключается сущность математической интуиции.

Примечания (сноски):