В литературе по космологии и математике можно встретить рассуждения о бесконечностях [1, 2], в которых делается ошибочный вывод о том, что в бесконечности часть может быть равна целому.
«множество натуральных чисел (![]() ) равномощно множествам целых чисел (
) равномощно множествам целых чисел (![]() ), чётных натуральных чисел, всех рациональных чисел (
), чётных натуральных чисел, всех рациональных чисел (![]() ), а отрезок числовой прямой (
), а отрезок числовой прямой (![]() , континуум) оказывается в биективном соответствии со всей числовой прямой (
, континуум) оказывается в биективном соответствии со всей числовой прямой (![]() ), а также с n-мерным евклидовым пространством (
), а также с n-мерным евклидовым пространством (![]() )» [1].
)» [1].
Для доказательства иногда предлагается записать четные числа в виде бесконечного ряда, а под этим рядом написать их порядковые номера из натурального ряда чисел:
2, 4, 6, 8, ... (1)
1, 2, 3, 4, ...
Здесь каждому четному числу соответствует один порядковый номер из натурального ряда чисел и наоборот. Значит, число четных чисел равно числу всех чисел натурального ряда. На первый взгляд это противоречит нашей интуиции. Ведь четные числа составляют лишь половину всех чисел. Это действительно так для любой конечной совокупности чисел, но не соответствует бесконечным рядам. Для бесконечных рядов получается, что их количества равны!
Но это неверно. Ошибка состоит в неверном способе подсчета. Произведём подсчет другим, правильным способом. Возьмем ряд всех натуральных чисел и будем их считать самым обычным, привычным способом. Для этого каждое натуральное число будем класть в ящик и называть его: один, два, три и так далее. Одновременно, по мере того, как нам будут встречаться эти числа, мы будем с каждым четным числом класть такую же цифру во второй ящик. И, для наглядности, с каждым нечётным – в третий ящик. Ну, и для ещё большей наглядности – каждое пятое число – в четвертый ящик.
Через некоторое время посмотрим, что у нас в ящиках? Через тысячу шагов, очевидно, в первом ящике будет 1 000 чисел. Во втором и третьем – по 500, а в четвертом – только 200. Ну, или в виде соотношения 10:5:5:2.
Продолжим раскладывать числа и вновь проверим содержимое ящиков через 10 000 шагов. И в этот раз мы обнаружим, что количества чисел в ящиках соотносятся как 10:5:5:2. Нужно ли доказывать, что и через миллион, и через миллиард и через гугл шагов количества чисел в ящиках будут соотноситься как 10:5:5:2?
Если мы последовательно синхронно считаем количества чисел в натуральном ряду, то мы найдём истинное соотношение их количеств. Однако, говорить, что бесконечное число всех натуральных чисел больше, чем число всех четных или нечетных чисел неправильно. Эти числа образуют бесконечности и можно говорить только об их мощности:
бесконечность всех натуральных чисел в два раза мощнее, чем бесконечности всех четных или нечетных чисел и в пять раз мощнее, чем бесконечность всех чисел, кратных пяти.
Кстати, также неправильно говорить в отношении бесконечностей, что часть может равняться целому. Правильно: мощность части бесконечности всегда меньше мощности всей бесконечности.
Рассмотрим приведённый выше пример в терминах мощностей. Примем без доказательства, что количество членов множества и его мощность – это разные, но схожие по смыслу понятия. Мы не можем сравнивать число членов множеств, по определению равных бесконечности, но мы можем сравнивать их мощности. Отношение мощностей М1 и М2 равномощных множеств всегда равно конечному, ненулевому числу с:
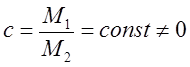
В этом случае отношение множеств (1) для четных чисел запишется в виде:
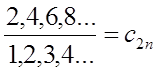
Запишем также и отношение множеств для нечетных чисел:
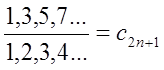
Далее нам понадобится и такое тождественное отношение:
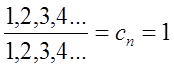
Это равенство очевидно, поскольку числитель равен знаменателю. Теперь просуммируем два отношения мощностей:
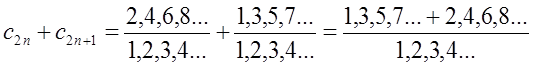
Очевидно, что последняя дробь содержит в числителе все целые натуральные числа:
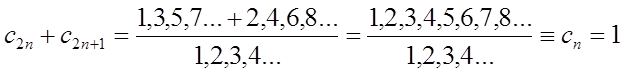
поэтому тождественно равна единице.
Это определённо означает, что мощности множеств всех натуральных чисел и суммы множеств всех четных и нечетных чисел равны. Но это также означает и равенство их бесконечного числа членов. Очевидно, что множества четных и нечетных чисел равномощны, поэтому, разделив полученное равенство на cn, получим:
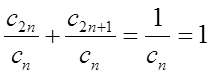
Из равенства следует, что мощности четных и нечётных чисел в два раза «слабее» мощности всех натуральных чисел:
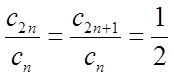
Отметим также без доказательств, что любые действия над каждым членом множества не изменяют мощности множества:
![]()
Из этого непосредственно следует, что решающее значение имеет способ, каким получено множество. Например, множество всех четных чисел может быть получено удалением из множества всех натуральных чисел нечётных или умножением на 2 каждого члена множества всех натуральных чисел:
![]()
Казалось бы, последнее выражение является точной копией множества всех четных чисел М(2, 4, 6, 8…). Но это ошибочно, поскольку любые действия над всеми (или отдельными) членами множества не изменяют их полного количества и, соответственно, мощности. Поэтому справедливо:
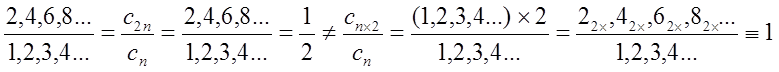
Хотя оба множества в числителях выглядят тождественно, на самом деле это разные множества, имеющие разную мощность.
В этой связи иногда можно встретить утверждение, будто математик Кантор доказал, что число точек на отрезке прямой сосчитать никаким способом нельзя. Их нельзя перенумеровать с помощью бесконечного ряда натуральных чисел, приписывая каждой точке свой номер, в каком бы порядке мы ни выбирали эти точки. Всегда останется хотя бы одна точка, на которую не хватит номера!
Это неверно сформулированное утверждение. Перенумеровать бесконечное количество чего-либо, действительно, невозможно. Однако, приводимое затем доказательство, как правило, начинается со слов: «Представим, что вопреки нашему утверждению кому-то удалось перенумеровать точки этого отрезка». Здесь следует напомнить фундаментальный принцип классической логики и классической математики, который постулирует полное отрицание актуальной бесконечности: «Infinitum Actu Non Datur» (Аристотель) – «актуальная бесконечность не существует». Принцип утверждает потенциальный, т.е. принципиально незавершаемый характер бесконечности множества. Актуальная, то есть, пересчитанная бесконечность лишена смысла. Бесконечностью может считаться лишь потенциальная бесконечность, завершить счет членов которой невозможно. Поэтому приводимое доказательство на этих словах можно и прервать – оно ошибочно. Впрочем, в этом вопросе Гильберту приписывается особое мнение. По мнению великого немецкого математика Давида Гилберта, главное различие между актуальной и потенциальной бесконечностью заключается вот в чём. Потенциально бесконечное есть всегда нечто возрастающее и имеющее пределом бесконечность, тогда как актуальная бесконечность – это завершённое целое, в действительности содержащее бесконечное число предметов [8].
Таким образом, ошибочным точно также являются и утверждения и доказательства равной мощности точек в прямом отрезке и, например, квадрата со стороной, равной этому отрезку. Мощность множества точек квадрата на отрезке имеет более высокий порядок, чем мощность множества точек отрезка. То есть, больше в бесконечное число раз.
Следует отметить, что вопросы бесконечных множеств сложны не только для рядовых математиков. Слабое понимание их приписывают иной раз и величайшим специалистам в этой области. Рассмотрим рассказ, который, как считается, где-то в третьем десятилетии 20 века предложил немецкий математик Давид Гильберт, один из величайших умов своего времени [2 - 6].
Представим себе гостиницу с бесконечным числом комнат. Комнаты пронумерованы натуральными числами от 1 до ∞. Однажды в гостиницу вошел человек и попросил снять комнату. К сожалению, для нового гостя не нашлось комнаты, так как отель был полностью заполнен бесконечным числом гостей, и не было ни одного свободного номера. Как предоставить новому гостю свободную комнату, не выселяя никого из постояльцев?
Несмотря на то, что задача явно говорит, что все номера заняты, утверждается, что есть возможность выделить сколько угодно свободных комнат. Для этого необходимо переселить постояльца из первой комнату во вторую, постояльца из второй комнаты в третью и так далее. То есть, каждого постояльца из комнаты с номером n необходимо переселить в комнату с номером n+1, n→n+1. В результате этого освобождается комната с номером один, и в неё можно поселить нового гостя.
Но это решение совершенно очевидно ошибочно. По условиям задачи определённо сказано, что свободных номеров нет! Следовательно, данный «парадокс» Гильберта является псевдопарадоксом [4]. В предложенном решении производится подмена понятий. Состояние, стационарное, неизменное – заполненность всех номеров жильцами – подменяется процессом, динамическим, движением – переселением постояльцев из одного номера в другой. Во-первых, этот процесс будет длиться вечность, во-вторых, в случае одного нового гостя, на всём протяжении процесса переселений один из постояльцев всегда будет без гостиничного номера, то есть, будет сидеть в коридоре, что является нарушением условия решения задачи. Для случаев множества новых гостей или их бесконечного числа, таких «временно не поселённых» будет соответствующее количество. Таким образом, решением «парадокса» является нелепость.
Следует отметить, немного отойдя от темы, что у Гильберта есть и другие примеры подмены понятий. Например, знаменитое гильбертовское доказательство V постулата Евклида. Аксиоматика Гильберта - это новая система аксиом евклидовой геометрии, которая мировым математическим разумом принята как безупречная. Она разработана Гильбертом в 1899 году как первая достаточно строгая и более полная аксиоматика, нежели система аксиом Евклида. Утверждается, что аксиомы Гильберта дали возможность точно сформулировать проблему V постулата, справедливость которого отрицается. Следствием этих положений является логически непротиворечивая система (неевклидова геометрия). Однако, и здесь видна подмена понятий. Из указанной аксиоматики негласно выброшен крайне важный III постулат Евклида. Поэтому утверждение, что к аксиомам I–IV присоединено положение, отрицающее справедливость аксиомы V, является ложным, поскольку не к полному набору аксиом I–IV, а только к их части – аксиомам I, II, IV! Напротив, включение в набор III постулата делает постулат V прямым следствием первых четырёх постулатов [7].
Литература
1.Википедия. Бесконечность. URL: https://ru.wikipedia.org/wiki/Бесконечность
2.Новиков И. Д., Черные дыры и Вселенная. — М.: Мол. гвардия, 1985. — 190 с., ил.— (Эврика), с.77, URL:
http://rusnauka.narod.ru/lib/phisic/blackwhole/Novik/blackn.htm
3.Гостиница Гильберта, http://forallx.ru/posts/hilberts-hotel-solution
4.Парадокс Гильберта, URL: http://traditio-ru.org/wiki/Парадокс_Гильбертa
5.Парадокс Гильберта (видео), URL:
http://pikabu.ru/story/paradoks_gilberta_1962200,
http://www.yaplakal.com/forum3/topic782267.html
6.Парадокс Гильберта, Википедия, URL: https://ru.wikipedia.org/wiki/Список_парадоксов
7.Путенихин П.В., Тайна третьего постулата, URL:
http://econf.rae.ru/article/7177 (дата обращения 02.04.2015)
http://samlib.ru/p/putenihin_p_w/postulat.shtml (дата обращения 02.04.2015)
8.Крейг У., Самое начало. Происхождение Вселенной и существование Бога, URL: http://www.otkrovenie.de/beta/xml/other/samoeNachalo.xml/3
